Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

296 Lectures on Dynamics of Stochastic Systems

the typical realization curve exponentially decreases at every spatial point, which

is indicative of cluster structure of energy ﬁeld; the increase of moments of mag-

netic energy is determined in this case by occasional, but great peaks of magnetic

energy against the typical realization curve, which are characteristic of lognormal pro-

cesses. Figure 8.4, page 209, schematically shows random realizations of magnetic

ﬁeld energy in random velocity ﬁeld for different signs of parameter α.

The indicator function of magnetic ﬁeld energy yields general understanding of the

spatial structure of the energy ﬁeld. In particular, functionals of the energy ﬁeld such

as the total volume (in the three-dimensional case) or area (in the two-dimensional

case) of the region in which E(r, t) > E,

V(t, E) =

dr θ

(

E(r, t) − E

)

∞

E δ



E(r, t) −



and the total energy contained in this region,

E(t, E) =

dr E(r, t)θ

(

E(r, t) − E

)

∞

E δ



E(r, t) −



whose averages are determined in terms of the one-point probability density (11.71),

are given in the general case by the equalities

V(t, E)

∞

dr P(r, t;

E),

E(t, E)

∞

dr P(r, t;

E).

The average values of these functionals are independent of the coefﬁcient of diffu-

sion in r-space (coefﬁcient D

), and, using probability density (11.71), we obtain the

expressions (8.58), page 210

V(t, E)

dr Pr



√

2Dt



(r)

−αt



E(t, E)

= e

γ t

dr E

(r) Pr



√

2Dt



(r)

(

2D−α

)



where function Pr(z) is deﬁned as (4.20), page 94.

Asymptotic expressions of function Pr(z) for z → ∞ and z → −∞ (4.23), page

95, offer a possibility of studying temporal evolution of these functionals. Namely,

Passive Tracer Clustering and Diffusion 297

for α > 0, average volume asymptotically decays with time (t → ∞) according to

the law

V(t, E)

≈

πE

α/D

−α

t/4D

α/D

(r).

On the contrary, for α < 0, average volume occupies the whole space for t → ∞.

In both cases, asymptotic behavior of total energy for t → ∞ has the form (because

α < 2D)

E(t, E)

≈ e

γ t

drE

(r)





1 −

(

2D − α

)

πt



(r)



(2D−α)/D

−

(

2D−α

)

t/4





where parameter γ is given by Eq. (11.73), which means that 100% of the total average

energy is contained in clusters for α > 0.

In the case of homogeneous initial conditions, the corresponding expressions with-

out integration over r present speciﬁc values of volume occupied by large peaks and

their total energy per unit volume:

V(t, E)

= Pr



√

2Dt



(r)

−αt



E(t, E)

= E

γ t



√

2Dt



(r)

(

2D−α

)



(11.76)

where parameter γ = D − α.

If we take section at level E > E

, then the initial values of these quantities will

be equal to zero at the initial instant,

V(0, E)

= 0 and

E(0, E)

= 0. Then, spatial

disturbances of energy ﬁeld appear with time and, for t → ∞, they are given by the

following asymptotic expressions:

V(t, E)

≈











πt





α/D

−α

t/4D

(α > 0),

1 −

|α|

πt





|α|/D

−|α|

t/4D

(α < 0)

and, because (2D − α) > 0,

E(t, E))

≈ E

γ t





1 −

(

2D − α

)

πt





(2D−α)/D

−(2D−α)

t/4D





298 Lectures on Dynamics of Stochastic Systems

Thus, for α > 0 (D

> D

), the speciﬁc total volume tends to zero and speciﬁc

total energy contained in this volume coincides with average energy in the whole

space, which is evidence of clustering the magnetic ﬁeld.

For α < 0 (D

< D

), no clustering occurs and speciﬁc volume occupies the whole

space in which speciﬁc average energy increases with time.

11.5 Integral One-Point Statistical Characteristics of

Passive Vector Fields

Above, we derived the equations for the one-point probability densities of the density

ﬁeld and magnetic ﬁeld under the assumption that effects of dynamic diffusion are

absent. The one-point probability densities allow calculating arbitrary one-point cha-

racteristics of these ﬁelds. Combined with the ideas of statistical topography, they are

sufﬁcient to obtain the conditions of possible formation of cluster structures. However,

the analysis of derivatives of these ﬁelds requires the knowledge of at least the two-

point probability densities. In principle, the equations for such probability densities

can be obtained in a standard manner, by using the general procedure for the linear

partial differential equations of the ﬁrst order. However, this derivation requires very

cumbersome calculations, and examination of consequences of such description is a

very difﬁcult task. Moreover, effects of dynamic diffusion cannot be included in such

probabilistic description.

We note however that, in the case of the delta-correlated random velocity ﬁeld with

absent average ﬂow, one can easily pass from linear Equations (11.1) and (11.2) to

closed equations for both average values of these ﬁelds by themselves and their higher

multi-point correlation functions.

For example, averaging Eq. (11.1), page 271, with the use of the Furutsu–Novikov

formula (11.14), page 276, and the expression for variational derivative

δρ(r, t)

δu

, t − 0)

= −

∂

∂r

δ(r − r

)ρ(r, t)

following from Eq. (11.1), page 271, we obtain the equation for tracer average

density

∂

∂t

ρ(r, t)



+ µ



ρ(r, t)

, (11.77)

where coefﬁcient D

is given by Eq. (4.54), page 107. Under condition D

 µ (µ 

cor

, where σ

is the variance and l

cor

is the spatial correlation radius of random

velocity ﬁeld), Eq. (11.77) coincides with the equation for the probability distribution

of particle coordinates (11.19), page 277, and, consequently, diffusion coefﬁcient D

characterizes only the scales of the region of tracer concentration in large and give

no data about the local structure of density realizations, as it was the case for the

diffusion in the nondivergent random velocity ﬁeld. In the case of the homogeneous

Passive Tracer Clustering and Diffusion 299

initial condition ρ(r, t) = ρ

, we obtain that

ρ(r, t)

= ρ

too, because random ﬁeld

ρ(r, t) is the nonstationary homogeneous random ﬁeld in this case, and average value

ρ(r, t)

is independent of r.

For this reason, it remains only one way to analyze the formulated problems,

which consists in studying the two-point correlation functions of the density ﬁeld

R(r, r

, t) =

ρ(r, t)ρ(r

, t)

and magnetic ﬁeld W

(r, r

, t) =



(r, t)H

, t)



. In

the case of the homogeneous initial conditions, these correlation functions depend on

difference (r −r

), which signiﬁcantly simpliﬁes the consideration. As we mentioned

earlier, all statistical averages in this case are the integral quantities, namely, the spe-

ciﬁc (per unit volume) quantities.

Various correlations of spatial derivatives of the ﬁelds under consideration can be

obtained by successive differentiation of the above correlation functions with respect

to spatial variables. The original stochastic equations must contain here dissipative

terms.

11.5.1 Spatial Correlation Function of Density Field

We start from Eq. (11.1) and ﬁrst of all draw a stochastic dynamic equation in function

R(r, r

, t) = ρ(r, t)ρ(r

, t),

∂

∂t

R(r, r

, t) = −



∂

∂r

(r, t) +

∂

∂r

, t)



R(r, r

, t)

+ µ

∂

∂r

∂

∂r

R(r, r

, t). (11.78)

Average Eq. (11.78) over an ensemble of realizations of random velocity ﬁeld.

Using then Furutsu–Novikov formula (11.14), page 276, we obtain that spatial corre-

lation function

R(r − r

, t)

R(r, r

, t)

ρ(r, t)ρ(r

, t)

satisﬁes the following equality

∂

∂t

R(r − r

, t)

= −



∂

∂r

(r − R) +

∂

∂r

− R)





δR(r, r

, t)

δu

(R, t − 0)



+ 2µ

(r − r

, t)

, (11.79)

where

(r − r

, t)

∂

∂r

R(r − r

, t)

, i.e., we use index notation for spatial

derivatives of function

R(r, t)

. Note that

(0, t)

< 0.

300 Lectures on Dynamics of Stochastic Systems

To calculate the variational derivative, omit in Eq. (11.78) the dynamic diffusion

term, which has no explicit dependence on the velocity ﬁeld, and write it in the form

∂

∂t

R(r, r

, t) = −



(r, t)

∂

∂r

+ u

, t)

∂

∂r



R(r, r

, t)

−



∂u

(r, t)

∂r

∂u

, t)

∂r



R(r, r

, t),

from which follows the equality



δR(r, r

, t)

δu

(R, t − 0)



= −



δ(r − R)

∂

∂r

+ δ(r

− R)

∂

∂r



R(r − r

, t)

−



∂δ(r − R)

∂r

∂δ(r

− R)

∂r



R(r − r

, t)

. (11.80)

Substituting now Eq. (11.80) in Eq. (11.79) and integrating the result over R, we obtain

the partial differential equation in the correlation function of the density ﬁeld. This

equation can be rewritten in the form (r − r

→ r)

∂

∂t

R(r, t)

= −

∂

(r) + B

(r)]

∂r

R(r, t)

−

∂[B

(r) + B

(r)]

∂r



(r, t)



−

∂[B

(r) + B

(r)]

∂r

(r, t)



(0) − B

(r) − B

(r)



(r, t)



+ 2µ

(r, t)

. (11.81)

In the special case of isotropic random velocity ﬁeld, random density ﬁeld ρ(r, t)

will be the homogeneous isotropic random ﬁeld. In this case the equation for the cor-

relation function becomes simpler and assumes the form

∂

∂t

R(r, t)

= 2µ

R(r, t)

∂

∂r

(r)

R(r, t)

where

(r) = 2



(0) − B

(r)



is the structure matrix of vector ﬁeld u(r, t).

In the absence of dynamic diffusion, this equation coincides with the equation for

the probability density of relative diffusion of two particles.

Correlation function

R(r, t)

will now depend on the modulus of vector r, i.e.,

R(r, t)

and, as a function of variables {r, t}, will satisfy the equation

∂

∂t

R(r, t)

d−1

∂

∂r

d−1



∂D

(r)

∂r



2µ +

(r)



∂

∂r



R(r, t)

Passive Tracer Clustering and Diffusion 301

where d is the dimension of space, as earlier. This equation has the steady-state solu-

tion

R(r, t)

R(r)

for t → ∞ [65, 66]

R(r)

= ρ

exp







∞

∂D

)/∂r

2µ + r

)/r







which corresponds to the boundary condition

R(∞) = ρ

Note that quantity

R(0)



(r, t)



t→∞

at r = 0 and, hence,

(r, t)

t→∞

= ρ

exp







∞

∂D

)/∂r

2µ + r

)/r







> ρ

. (11.82)

Now, we turn back to the general case of random velocity ﬁeld not having specular

symmetry (i.e., possessing helicity). Setting r = 0 in Eq. (11.81) and taking into

account Eq. (4.57), page 107, we arrive at the nonclosed equation



∂

∂t

− 2D



R(0, t)

= 2µ

(0, t)

R(0, 0)

= ρ

. (11.83)

To approximately solve Eq. (11.83), we construct an approximate procedure based

on the expansion of its right-hand side in series in small parameter µ

. With this

goal in view, mark quantities

R(0, t)

and

(0, t)

by subscript µ and rewrite

Eq. (11.83) in the form of nonclosed integral equation

R(0, t)

= ρ

exp







t +

dτ

2µ

R(0, τ )

(0, τ )







. (11.84)

At the initial step when dissipation can be neglected, the solution has the form

R(0, t)

(r, t)

= ρ

, (11.85)

which, naturally, coincides with Eq. (11.48) for n = 2 and depends only on the poten-

tial component of the spectral function of velocity ﬁeld.

Then, we represent the right-hand side in the form of a series in parameter µ. In the

ﬁrst approximation the solution of the problem has the following structure

R(0, t)

= ρ

exp







t +

dτ

2µ

R(0, τ )

(0, τ )







. (11.86)

302 Lectures on Dynamics of Stochastic Systems

Running a few steps forward, we note that, in view of the exponential increase with

time of all moment functions in the problem under consideration, solution (11.86)

exponentially increases for small times, reaches a maximum at time instant t

max

, and

then rapidly decreases with time in accordance with physical meaning of the problem

under consideration.

Note now that a corollary of the structure of Eq. (11.81) is the fact that helicity of

the velocity ﬁeld has no effect on statistics of the density ﬁeld gradient. Indeed, all

coefﬁcients of this equation contain only symmetric matrix



(r) + B

(r)



, and all

odd-order derivatives of such a matrix with respect to r vanish at r = 0 (see Eq. (4.58),

page 107). Odd-order derivatives of function

R(r, t)

vanish at r = 0 in exactly the

same way. In view of these facts, we can say that helicity of the gradient of tracer

density is equal to zero, because it is determined by quantity



∂ρ(r, t)

∂r

∂

ρ(r, t)

∂r





ijk

(0, t)



11.5.2 Spatial Correlation Tensor of Density Field Gradient and

Dissipation of Density Field Variance

Introduce now the vector of density ﬁeld gradient p

(r, t) =

∂ρ(r, t)

∂r

; then, the spatial

correlation tensor of density ﬁeld gradient is deﬁned by the equality

(r − r

, t) =



∂ρ(r, t)

∂r

∂ρ(r

, t)

∂r



≡ −

(r − r

, t)

and variance of the density ﬁeld gradient is given by the formula

(t) =



∂ρ(r, t)

∂r



≡ −

(0, t)

. (11.87)

Note that, for t → ∞, expression for steady-state variance of the density ﬁeld

gradient follows from Eq. (11.83)

(∞) =

R(0, ∞)

To determine temporal evolution of the spatial correlation tensor of density ﬁeld

gradient, we differentiate Eq. (11.81) with to r

. As a result, we obtain the equation

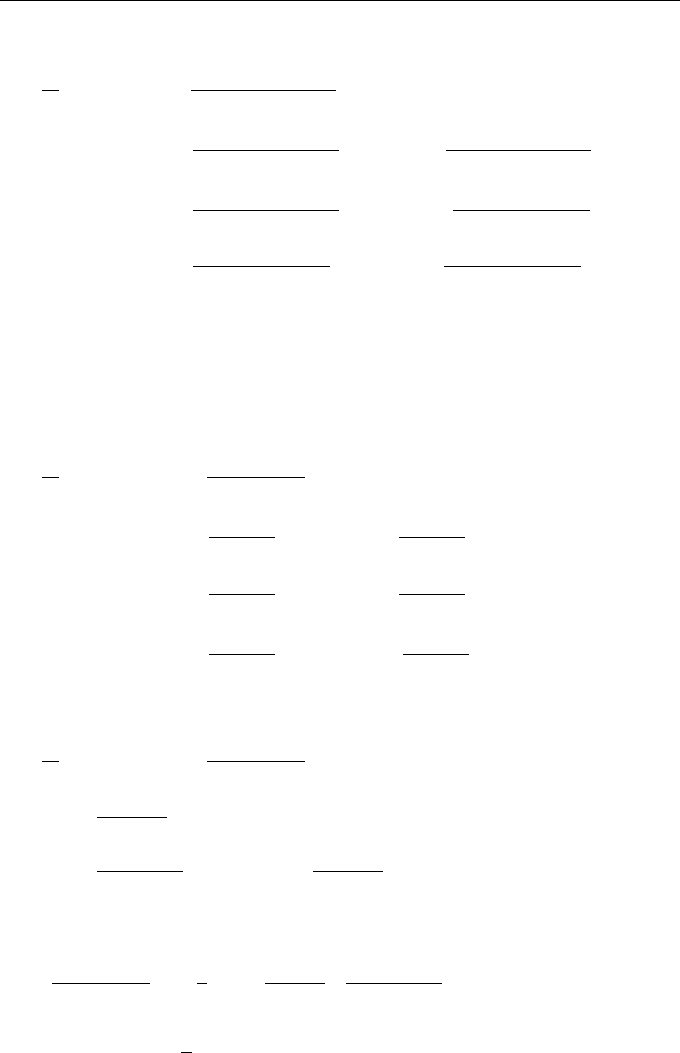
Passive Tracer Clustering and Diffusion 303

(r − r

→ r)

∂

∂t

(r, t)

= −

∂

(r) + B

(r)]

∂r

R(r, t)

−

∂

(r) + B

(r)]

∂r



(r, t)



−

∂

(r) + B

(r)]

∂r

(r, t)

−

∂

(r) + B

(r)]

∂r

(r, t)

−

∂[B

(r) + B

(r)]

∂r



(r, t)



−

∂[B

(r) + B

(r)]

∂r



(r, t)



−

∂[B

(r) + B

(r)]

∂r

(r, t)

−



(0) − B

(r) − B

(r)



jik

(r, t)



Vector

(r, t)

describes the spatial correlation of the density ﬁeld and its gradi-

ent, and all terms of this equation are identically equal to zero at r = 0.

Differentiating this equation with respect to r

and setting r = 0, we obtain the

equation

∂

∂t

(0, t)

= −2

∂

(0)

∂r

R(0, t)

− 2

∂

(0)

∂r



(0, t)



− 2

∂

(0)

∂r



(0, t)



− 2

∂

(0)

∂r



(0, t)



− 2

∂

(0)

∂r

(0, t)

− 2

∂

(0)

∂r

(0, t)

− 2

∂

(0)

∂r

(0, t)

Using Eq. (4.57), page 107, we can rewrite this equation in the form

∂

∂t

(0, t)

= −2

∂

(0)

∂r

R(0, t)

+ 2

d(d + 2)

[

(d + 1)δ

(0, t)

− 2

(0, t)

]

+ 2

(

4 + d

)

(0, t)

+ 2

d(d + 2)

[

(0, t)

+ 2

(0, t)

]

Then, because the source of the gradient ﬁeld

∂

(0)

∂r

= −

∞

dτ



∂u(r, t)

∂r

∂u(r, t − τ )

∂r



(4)

, (D

(4)

> 0)

304 Lectures on Dynamics of Stochastic Systems

is isotropic, tensor

(0, t)

is also isotropic, i.e.,

(0, t)

Consequently, the variance of the density ﬁeld gradient (11.87) satisﬁes the equation

∂

∂t

(0, t)

= −D

(4)

R(0, t)

+ 2

(d − 1) +

(

d + 5

)

(0, t)

(11.88)

where the second moment of density ﬁeld

R(0, t)

is given by Eq. (11.85).

The solution to Eq. (11.88) has the form

(t) =

(4)

R(0, t)

− 1

, (11.89)

where parameter A = 2

(d − 1) + 5D

Note that this solution is generated by the potential component of spectral density

of random velocity ﬁeld; however, in the case of weak compressibility (D

 D

)

the increment of the exponential increase in time of the solution coincides with the

increment of the variance of density ﬁeld gradient in noncompressible ﬂow of liquid

with the inhomogeneous initial distribution, because parameter A = 2

(d − 1)

this case.

Now, we turn back to Eq. (11.86) and use Eq. (11.89) to rewrite it in the ﬁnal form

(t)

= ρ

exp

(

t − 2

(4)

− 1 − At

)

. (11.90)

This solution has a maximum at

max

≈ ln

(4)

and quantity

R(0, t)

reaches at this moment the value

R(0, t)

1max

≈ ρ

(4)

exp



−



The condition

t  t

max

is the applicability condition of neglecting the effects of dynamic diffusion. For t >

max

function

R(0, t)

rapidly decreases with time. As we mentioned earlier, quantity

R(0, t)

in the general case tends to steady-state value (11.82) for t → ∞.

Passive Tracer Clustering and Diffusion 305

Let us demonstrate that the suggested method of describing temporal dynamics of

statistical characteristics with inclusion of the effects of dynamic diffusion remains

valid in more general cases, such as describing dynamics of the variance of density

gradient (11.87). To obtain this dynamics, we must include the term with dynamic

diffusion in Eq. (11.88) and replace subscript 0 with subscript µ. As a result, we arrive

at the equation

∂

∂t

(0, t)

= −D

(4)

R(0, t)

+ B

(0, t)

+ 2µ

kkll

(0, t)

where coefﬁcient B = 2

(d − 1) +

(

d + 5

)

. Rewrite this equation in the form

∂

∂t

(0, t)

= −D

(4)

R(0, t)



B + 2µ

kkll

(0, t)



(0, t)

The corresponding solution has the form

(0, t)

= −D

(4)

R(0, t

)

exp









B + 2µ

kkll

(0, t

)

(0, t









and, consequently, in the ﬁrst approximation in the coefﬁcient of molecular diffusion,

we obtain the expression

(0, t)

= −D

(4)

R(0, t

)

exp









B + 2µ

kkll

(0, t

)

(0, t









where quantity

R(0, t)

is described by Eq. (11.90). As for quantity

kkll

(0, t)

, it

satisﬁes the equation without effects of dynamic diffusion, which can be derived by

the standard procedure.

Extension to the Case of Inhomogeneous Initial Conditions

We considered a number of problems on dynamics of statistical characteristics of the

density ﬁeld and its gradient and solved them in the simplest statement (with the homo-

geneous initial conditions) with the minimal set of governing parameters concerning

only statistical characteristics of the homogeneous velocity ﬁeld, which is assumed to

be the ﬁeld delta-correlated in time. In this case, all ﬁelds under study are also spa-

tially homogeneous random ﬁelds, but they are nonstationary in time. This means that

statistical averages like F

(r, r

, t) =



(r, t)f

, t)



depend only on the difference of

spatial coordinates (r − r

) and, consequently,

∂

∂r

(r, r

, t) = −

∂

∂r

(r, r

, t),