Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

306 Lectures on Dynamics of Stochastic Systems

i.e., at r = r

, quantity



(r, t)

∂f

(r, t)

∂r



, independent of r and satisﬁes the identity



(r, t)

∂f

(r, t)

∂r



= −



(r, t)

∂f

(r, t)

∂r



, (11.91)

which we widely used in derivation of all equations. This relationship signiﬁcantly

simpliﬁed the analysis of both dynamic system by itself and obtained results, because

majority of terms vanished at r = r

, which means the absence of advection of statis-

tical characteristics in the considered problems. Namely this fact allowed us to com-

pletely solve the considered problems and without very cumbersome calculations.

In the case of inhomogeneous initial conditions, solutions of all problems lose the

property of spatial homogeneity, and the equations become very cumbersome. How-

ever, the solutions obtained above yield certain data in this case, too. Indeed, property

(11.91) holds also for integral (integration by parts)

dr f

(r, t)

∂f

(r, t)

∂r

= −

dr f

(r, t)

∂f

(r, t)

∂r

Therefore, it is clear that the density ﬁeld for inhomogeneous initial conditions with

absent dynamic diffusion will be described, instead of Eq. (11.85), by the solution of

the form

(r, t)

dr ρ

(r)e

, (11.92)

and Eq. (11.89) will be replaced with the expression

(

∇ρ(r, t)

)

(

∇ρ

(r)

)

(4)

(r, t)

− 1

, (11.93)

where B = 2

(d − 1) + (d + 5)D

Thus, we can assert that the obtained relationships and associations between dif-

ferent quantities become the integral ones in the context of inhomogeneous problems

and form, in ﬁgurative words, a skeleton (reference points) that provide a background

for the dynamics of complicated stochastic motions. In addition, for inhomogeneous

problems, all terms vanished in the above consideration have the divergent (‘ﬂow-

like’) form.

In the same way, we can easily draw an analog of Eq. (11.86) for the variance

of density ﬁeld with inclusion of variance dissipation in the case of inhomogeneous

problems. For example, solution (11.86) is replaced with the expression for the whole

Passive Tracer Clustering and Diffusion 307

temporal interval

(r, t)

dr ρ

(r) exp











t − 2µ

dτ

(

∇ρ(r, τ )

)

(r, τ )











where functions in the right-hand side are given by Eqs. (11.92) and (11.93).

Diffusion of Density Field with Constant Gradient

As we mentioned earlier, in the presence of velocity ﬁeld ﬂuctuations, the initially

smooth distribution of tracer becomes increasingly inhomogeneous with time, there

appear changes within increasingly shorter scales, and concentration spatial gradients

sharpen. In actuality, dynamic diffusion smooths these processes, so that the men-

tioned behavior of tracer concentration holds only for limited temporal intervals.

In the presence of dynamic diffusion, the tracer diffusion is described in terms

of the second-order partial differential equation (11.1), page 271. Problems in which

mean concentration gradient assumes nonzero values allow a more complete analysis

for the nondivergent (noncompressible) velocity ﬁeld.

This case corresponds to solving Eq. (11.1) with the following initial conditions

(here, we again content ourselves with the two-dimensional case)

(r) = Gr, p

(r) = G.

Substituting the concentration ﬁeld in the form

ρ(r, t) = Gr + eρ(r, t),

we obtain the equation for ﬂuctuating portion eρ(r, t) of the concentration ﬁeld



∂

∂t

∂

∂r

u(r, t)



eρ(r, t) = −Gu(r, t) + µ1eρ(r, t), eρ(r, 0) = 0. (11.94)

Unlike the problems discussed earlier, the solution to this problem is the random

ﬁeld statistically homogeneous in space, so that all one-point statistical averages are

independent of r and steady-state probability densities exist for t → ∞ for both con-

centration ﬁeld and its gradient.

In this case, Eq. (11.94) easily yields the equation



eρ

(r, t)



= n(n − 1)D

eρ

n−2

(r, t)

− µn(n − 1)

eρ

n−2

(r, t)ep

(r, t)

(11.95)

where

ep(r, t) =

∂

∂r

eρ(r, t) = p(r, t) − G.

308 Lectures on Dynamics of Stochastic Systems

In the steady-state regime (for t → ∞), we obtain from Eq. (11.95) that

eρ

n−2

(r, t)ep

(r, t)

eρ

n−2

(r, t)

. (11.96)

For n = 2 in particular, we obtain the expression for the variance of concentration

gradient ﬂuctuations

lim

t→∞

(r, t)

. (11.97)

Rewrite now Eq. (11.95) in the form



eρ

(r, t)



= n(n − 1)D

f (r, t)eρ

n−2

(r, t)

, (11.98)

where

f (r, t) = 1 −

(r, t).

Consequently, the variance of concentration is given by the expression

(

eρ(r, t)

= 0

)

eρ

(r, t)

= 2D

dτ

f (r, τ )

. (11.99)

Note that the correlation function of ﬁeld eρ(r, t),

0(r, t) =

eρ(r

, t)eρ(r

, t)

, r = r

− r

satisﬁes the equation

∂

∂t

0(r, t) = 2G

(r) + 2



(0) − B

(r) + µδ



∂

∂r

0(r, t)

that follows from Eq. (11.94); consequently, its steady-state limit

0(r) = lim

t→∞

0(r, t)

satisﬁes the equation

(r) = −



(0) − B

(r) + µδ



∂

∂r

0(r). (11.100)

Setting r = 0 in this equation and taking into account Eqs. (4.54), page 107, we

arrive at equality (11.97). If we differentiate Eq. (11.100) two times with respect to r

Passive Tracer Clustering and Diffusion 309

and then set r = 0 and take into account Eqs. (4.56) and (4.57), page 107, we obtain

the equality

(

1eρ(r, t)

)

+ µ)G

. (11.101)

Exact equalities (11.97) and (11.101) can appear practicable for testing different

numerical schemes and checking simulated results. However, the calculation of the

steady-state limit



eρ

(r, t)



for t → ∞ requires the knowledge of temporal behavior

of the second moment



(r, t)



, which can be obtained only if dynamic diffusion

is absent. In this case, the probability density of the concentration gradient satisﬁes

Eq. (11.57); in the problem under consideration, this equation assumes the form

∂

∂t

P(r, t;p) =



∂

∂p

− 2

∂

∂p



P(r, t;p),

P(0, r;p) = δ

(

p − G

)

(11.102)

Consequently, according to Eq. (11.61), we have

|ep(r, t)|

= G

− 1

. (11.103)

The exact formula (11.97) and Eq. (11.103) give a possibility of estimating the time

required for quantity



(r, t)



to approach the steady-state regime for t → ∞; namely,

∼ ln



+ µ



As a consequence, we obtain from Eq. (11.99) the following estimate of the steady-

state variance of concentration ﬁeld ﬂuctuations

lim

t→∞

eρ

(r, t)

∼ 2



+ µ



Taking into account the fact that D

∼ σ

and D

∼ l

(σ

is the variance of

velocity ﬁeld ﬂuctuations and τ

and l

are this ﬁeld temporal and spatial correlation

radii, respectively), we see that time T

, in view of its logarithmic dependence on

dynamic diffusion coefﬁcient µ, can be not very long,

≈





and quantity

eρ

∼ G





for µ  σ

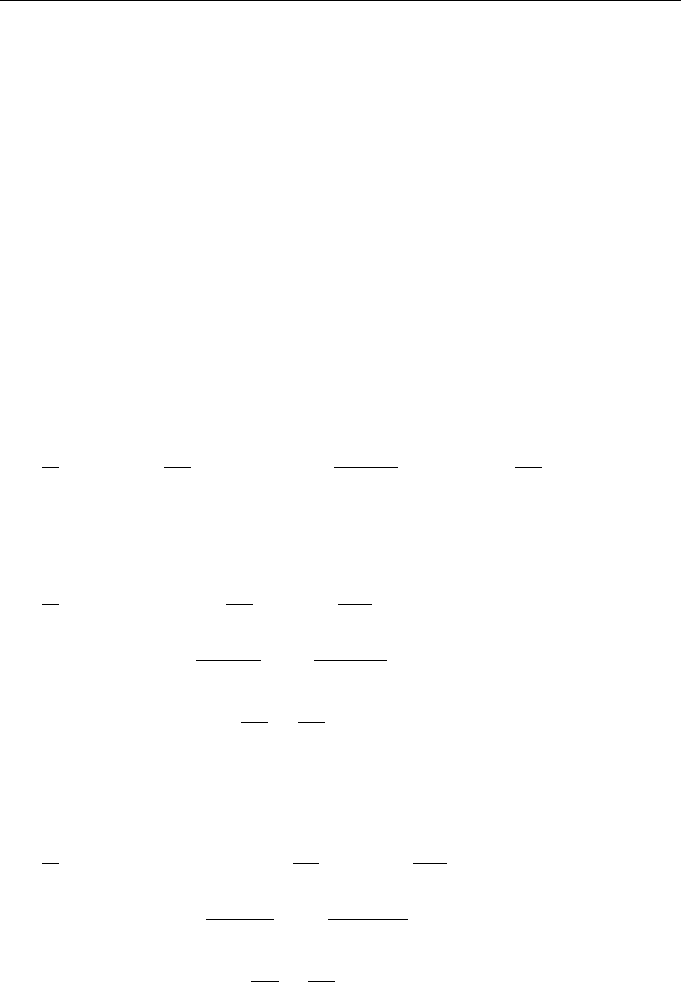
310 Lectures on Dynamics of Stochastic Systems

11.5.3 Spatial Correlation Function of Magnetic Field

As was mentioned earlier, in the general case of the divergent random velocity ﬁeld,

we can calculate one-point statistical characteristics of magnetic ﬁeld and magnetic

energy, such as their probability densities. Under the neglect of dynamic diffusion,

this technique is, in principle, applicable for calculating different quantities related to

the spatial derivatives of magnetic ﬁeld. However, the corresponding equations appear

to be very cumbersome, and their use for derivation of comprehensible consequences

is hardly possible.

In the analysis of different moment functions, we can take into account the coefﬁ-

cient of dynamic diffusion. However, in the general case of the divergent velocity ﬁeld,

all equations will be very cumbersome again. For this reason, we restrict ourselves to

the nondivergent velocity ﬁeld (div u(r, t) = 0), i.e., we will analyze statistical charac-

teristics of spatial derivatives of magnetic ﬁeld in a noncompressible turbulent ﬂow.

Inclusion of compressibility only changes the coefﬁcients of the corresponding equa-

tion, but not the basic tendency of the behavior of moment functions.

Rewrite the vector equation (11.2) in the coordinate form,

∂

∂t

(r, t) = −

∂

∂r

(r, t)H

(r, t) +

∂u

(r, t)

∂r

(r, t) + µ

∂

∂r

(r, t),

and introduce function W

(r, r

;t) =H

(r, t)H

, t). This function satisﬁes the

equation

∂

∂t

(r, r

;t) =



−



∂

∂r

(r, t) +

∂

∂r

, t)



∂u

(r, t)

∂r

∂u

, t)

∂r



(r, r

;t)

+ µ

∂

∂r

∂

∂r

(r, r

;t). (11.104)

In view of solenoidal property of the velocity ﬁeld, Eq. (11.104) can be rewritten in

the form

∂

∂t

(r, r

;t) =



−



(r, t)

∂

∂r

+ u

, t)

∂

∂r



∂u

(r, t)

∂r

∂u

, t)

∂r



(r, r

;t)

+ µ

∂

∂r

∂

∂r

(r, r

;t). (11.105)

Equation (11.104) is convenient for immediate averaging, and Eq. (11.105) is con-

venient for calculating the variational derivative.

Passive Tracer Clustering and Diffusion 311

As earlier, we assume that ﬁeld u(r, t) is the homogeneous (but generally not

isotropic) Gaussian ﬁeld stationary and delta-correlated in time with correlation func-

tion (11.13), page 276 and use the Furutsu–Novikov formula (11.14), page 276 to split

correlations. Then, averaging Eq. (11.104) over an ensemble of realizations of random

ﬁeld u(r, t) and using the variational derivative in the form



δW

(r, r

;t)

δu

(R, t − 0)





−



δ(r − R)

∂

∂r

+ δ(r

− R)

∂

∂r



∂δ(r − R)

∂r

∂δ(r

− R)

∂r



(r, r

;t)

following from Eq. (11.105), we obtain the partial differential equation

(

r − r

→ r

)

∂

∂t



(r;t)



= −2

∂

(r)

∂r

(r;t)

− 2

∂[B

(0) − B

(r)]

∂r

∂

∂r



(r;t)



− 2

∂[B

(0) − B

(r)]

∂r

∂

∂r

(r;t)



(0) − B

(r) − B

(r)



∂

∂r



(r;t)



+ 2µ



ij;ss

(r;t)



(11.106)

where



ij;ss

(r;t)



is the dissipative tensor,



ij;ss

(r;t)



∂

∂r



(r;t)



Setting r = 0 in Eq. (11.106), we obtain the unclosed equation in the one-point

correlation,

∂

∂t



(t)



= −2

∂

(0)

∂r

(t)

+ 2µ



ij;ss

(0;t)



Then, taking into account the solenoidal portion of Eq. (4.57), page 107, (D

= 0), we

arrive at the unclosed equation in the correlation of the form

∂

∂t



(t)



2(d + 1)D

d(d + 2)

E(t)

−

d(d + 2)



(t)



+ 2µ



ij;ss

(0;t)



(11.107)

where

E(t)



(r, t)



is the average energy of magnetic ﬁeld. Setting i = j in

Eq. (11.107), we obtain the equation in average energy

∂

∂t

E(t)

2(d − 1)D

E(t)

− 2µ

D(t),

312 Lectures on Dynamics of Stochastic Systems

where quantity D(t) describing dissipation of average energy of the nonstationary ran-

dom magnetic ﬁeld is deﬁned by the equality,

D(t) =

[

rot H(r, t)

]

= −

∂

∂r

H(r, t)H(r

, t)

= −

∂

∂r

(r − r

, t)

= −



ii;jj

(0, t)



, (11.108)

where W

(r, r

, t) = H

(r, t)H

, t) and the derivatives of this function are denoted

by additional indices after semicolon ‘;’. As in the case of the analysis of statistical

characteristics of the density ﬁeld, we mark all quantities by subscript µ and rewrite

this equation in the form

∂

∂t

E(t)

2(d − 1)D

−

2µ

E(t)

(t).

Then, we expand the right-hand side of this equation in series in parameter µ. In

the ﬁrst approximation, we have the equation

∂

∂t

E(t)

2(d − 1)D

−

2µ

E(t)

(t),

where quantities with subscript 0 correspond to the solution of the problem under the

neglect of the effect of dynamic diffusion. Thus, in the ﬁrst approximation, the solution

to the problem has the structure

E(t)

= E

exp







2(d − 1)D

−

dτ

2µ

E(τ )

(τ )







. (11.109)

At the initial evolutionary stage when dissipation can be neglected, the solution to

the problem exponentially increases,

E(t)

= E

exp



2(d − 1)



, (11.110)

and the equation in correlation (11.107) in the absence of dynamic diffusion grades

into the equation with a given source, and the solution of the latter equation has the

form



(t)



E(t)



(0)

−



exp



−2



d + 1

d + 2





, (11.111)

i.e., magnetic ﬁeld in noncompressible turbulent ﬂow of a liquid becomes rapidly

isotropic (fast isotropization of magnetic ﬁeld). Note that compressibility of the ran-

dom ﬂow increases the rate of average energy increase and makes isotropization of

magnetic ﬁeld faster (cf. with Eq. (11.68), page 293).

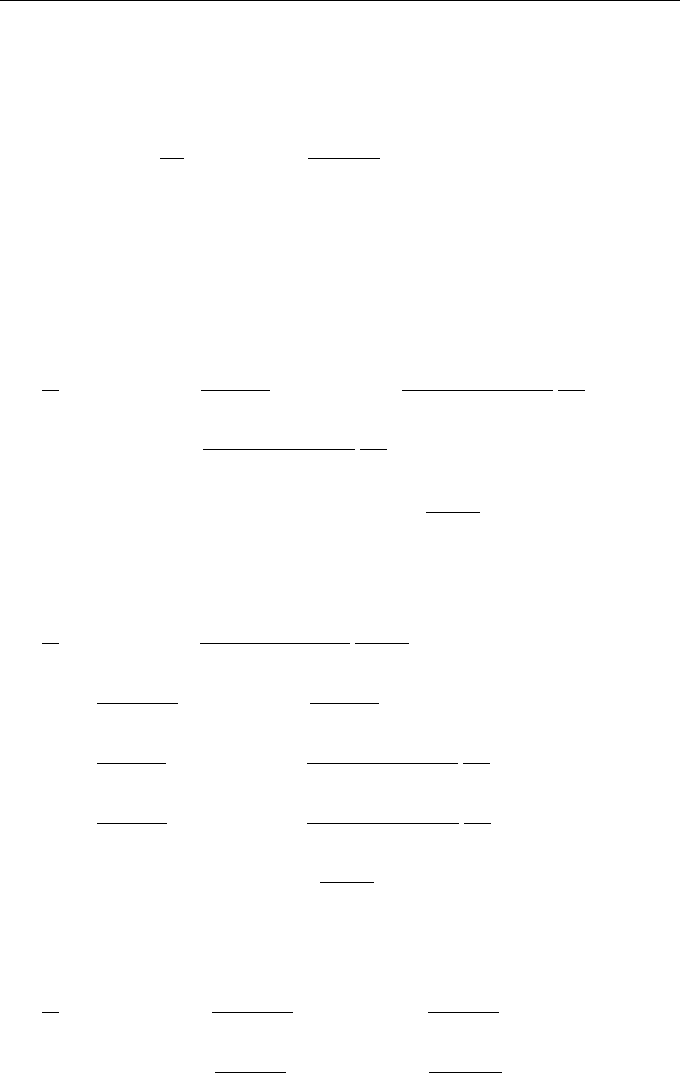
Passive Tracer Clustering and Diffusion 313

11.5.4 On the Magnetic Field Helicity

In what follows, we neglect dynamic diffusion and omit subscript 0. Here, we derive

an equation for quantity



kp;j

(r;t)



∂

∂r



(r;t)





∂H

(r, t)

∂r

, t)



with the goal of calculating magnetic ﬁeld helicity

H(t) = ε

ijk



ki;j

(0;t)



H · rot H

Rewriting Eq. (11.106) in the form

∂

∂t



(r;t)



= −2

∂

(r)

∂r

(r;t)

− 2

∂[B

(0) − B

(r)]

∂r

∂

∂r



(r;t)



− 2

∂[B

(0) − B

(r)]

∂r

∂

∂r

(r;t)



(0) − B

(r) − B

(r)



∂

∂r



(r;t)



and differentiating it with respect to r

, we obtain the equation

∂

∂t



kp;j

(r;t)



= −

∂[B

(r) + B

(r)]

∂r

∂

∂r



(r;t)



− 2

∂

(r)

∂r

(r;t)

− 2

∂

(r)

∂r



nm;j

(r;t)



+ 2

∂

(r)

∂r



mp;n

(r;t)



− 2

∂[B

(0) − B

(r)]

∂r

∂

∂r



mp;j

(r;t)



+ 2

∂

(r)

∂r



km;n

(r;t)



− 2

∂[B

(0) − B

(r)]

∂r

∂

∂r



km;j

(r;t)





(0) − B

(r) − B

(r)



∂

∂r



kp;j

(r;t)



. (11.112)

Then, setting r = 0, we pass to the equation in the one-point correlation

∂

∂t



kp;j

(0;t)



= −2

∂

(0)

∂r

(0;t)

− 2

∂

(0)

∂r



nm;j

(0;t)



+ 2

∂

(0)

∂r



mp;n

(0;t)



+ 2

∂

(0)

∂r



km;n

(0;t)



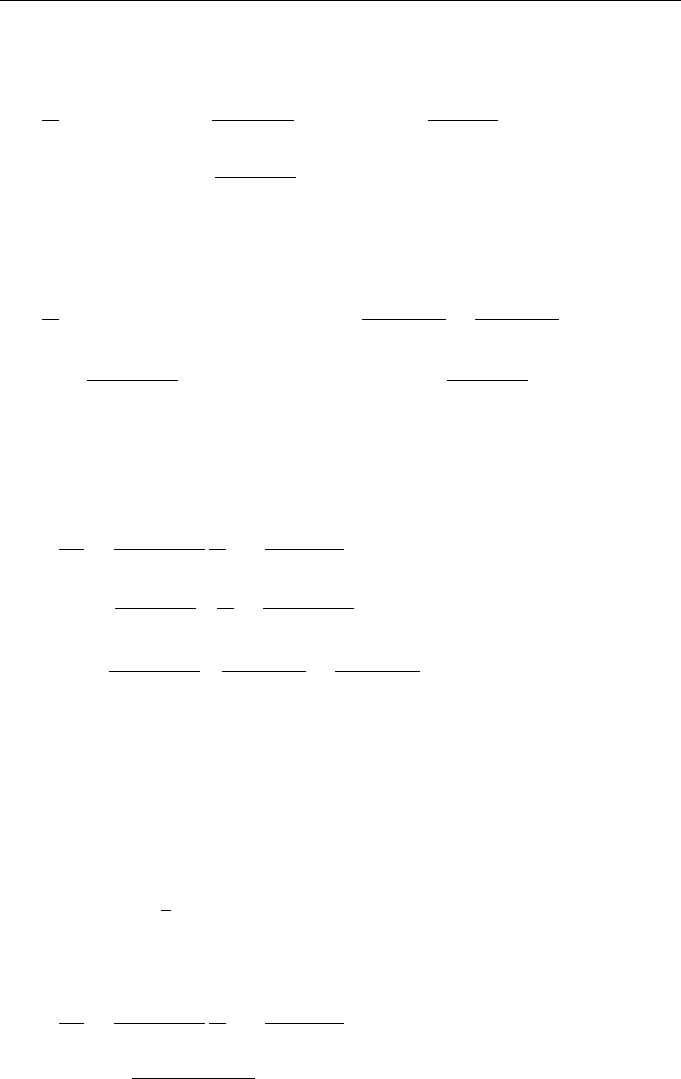
314 Lectures on Dynamics of Stochastic Systems

Using Eq. (4.57), page 107, for the solenoidal portion of the correlation function,

we obtain the equation

∂

∂t



kp;j

(0;t)



= −2

∂

(0)

∂r

(0;t)

+ 4

d(d + 2)



kp;j

(0;t)



− 2

(d + 1)D

d(d + 2)



jp;k

(0;t)





kj;p

(0;t)



Now, we must draw an equation for function



jp;k

(0;t)





kj;p

(0;t)



. It has the

form

∂

∂t



jp;k

(0;t)





kj;p

(0;t)



= −2

∂

(0)

∂r

∂

(0)

∂r

(0;t)

2(d + 3)D

d(d + 2)



jp;k

(0;t)





kj;p

(0;t)



− 4

(d + 1)D

d(d + 2)



kp;j

(0;t)



Thus, we arrive at the system of equations in functions



kp;j

(0;t)



and



jp;k

(0;t)





kj;p

(0;t)



with zero-valued initial conditions, or to the second-order

equation



∂

∂t

−

2(d + 5)D

d(d + 2)

∂

∂t

− 8

(d − 1)

(d + 2)









kp;j

(0;t)



= −2

∂

(0)

∂r



∂

∂t

−

2(d + 3)D

d(d + 2)



(0;t)

4(d + 1)D

d(d + 2)

∂

(0)

∂r

∂

(0)

∂r

(0;t)

(11.113)

with the source resulting from to the absence of reﬂection symmetry in the right-hand

side.

Expand function C(r) in the correlation function of velocity ﬁeld (4.59), page 108,

C(r) = C(0) − αr

+ ···, and use Eq. (4.58), page 107. We will solve Eq. (11.113)

proceeding from the increasing exponents of the one-point correlation function of

magnetic ﬁeld (11.110) and (11.111)

(0;t)

E(t)

In this case, Eq. (11.113) becomes simpler and assumes the form of the equation



∂

∂t

−

2(d + 5)D

d(d + 2)

∂

∂t

− 8

(d − 1)

(d + 2)









kp;j

(0;t)



= 8αD

(

d + 3

) (

d − 1

)

kpj

E(t)

Passive Tracer Clustering and Diffusion 315

which can be rewritten in the form



∂

∂t

−



∂

∂t

2(d − 1)D

d(d + 2)





kp;j

(0;t)



= 8αD

(

d + 3

) (

d − 1

)

kpj

E(t)

(11.114)

Equation (11.114) has two characteristic exponents, positive one, corresponding to

the increasing exponent, and negative, corresponding to the damped solution. We will

seek the increasing solution to Eq. (11.114) in the form



kp;j

(0;t)



= U(t) exp





Here, function U(t) satisﬁes the simpler ‘abridged’ equation

∂U(t)

∂t

= 4αε

kpj

(d + 2)(d − 1)(d + 3)

(

d + 1

)

exp



2(d − 3)D



We mentioned that helicity is equal to zero in the two-dimensional case. In the three-

dimensional case, we have

U(t) = 20αε

kpj

and, consequently, the main exponentially increasing solution assumes the form



kp;j

(0;t)



= U(t) exp





= 20αε

kpj

E(t)

t. (11.115)

Taking into account Eq. (1.54) (in the three-dimensional case ε

ijk

kij

= 6), we

obtain the ﬁnal expression for helicity of magnetic ﬁeld

(t) = 120α

E(t)

t. (11.116)

11.5.5 On the Magnetic Field Dissipation

Dissipation of magnetic ﬁeld is deﬁned by Eq. (11.108), and calculation of its value

requires knowledge of quantity



kp;js

(0;t)



∂

∂r



kp;j

(0;t)





∂H

(r, t)

∂r

, t)



r=r