Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

286 Lectures on Dynamics of Stochastic Systems

where Pr(z) is the probability integral (4.20), page 94, and we use the dimensionless

time τ = D

In the context of the one-point characteristics of density ﬁeld ρ(r, t), the problem

is statistically equivalent in this case to the analysis of a random process; hence, all

moment functions beginning from the second one appear to be exponentially increas-

ing functions of time

ρ(r, t)

= ρ



(r, t)



= ρ

n(n−1)τ

, (11.48)

and in accordance with Eqs. (4.60), page 108, the typical realization curve of the

concentration ﬁeld exponentially decays with time at any ﬁxed spatial point

∗

(t) = ρ

−τ

which is evidence of cluster behavior of medium density ﬂuctuations in arbitrary

divergent ﬂows. The Eulerian concentration statistics at any ﬁxed point is formed due

to concentration ﬂuctuations about this curve.

Even the above discussion of the one-point probability density of tracer concentra-

tion in the Eulerian representation revealed several regularities concerning the tempo-

ral behavior of concentration ﬁeld realizations at ﬁxed spatial points. Now we show

that this distribution additionally allows us to reveal certain features in the space–time

structure of concentration ﬁeld realizations.

For simplicity, we content ourselves with the two-dimensional case. As was men-

tioned earlier, the analysis of level lines deﬁned by the equality ρ(r, t) = ρ = const

can give important data on the spatial behavior of realizations, in particular, on differ-

ent functionals of the concentration ﬁeld, such as total area S(t, ρ) of regions where

ρ(r, t) > ρ and total tracer mass M(t, ρ) within these regions. Average values of these

functionals can be expressed in terms of the one-point probability density:

S(t, ρ)

∞

deρ

dr P(r, t;eρ),

M(t, ρ)

∞

eρdeρ

dr P(r, t;eρ). (11.49)

Substituting the solution to Eq. (11.46) in these expressions and performing some

rearrangement, we easily obtain explicit expressions for these quantities

S(t, ρ)

dr Pr



√

2τ



(r)e

−τ



M(t, ρ)

dr ρ

(r) Pr



√

2τ



(r)e



(11.50)

where probability integral Pr(z) is deﬁned as Eq. (4.20), page 94. Taking into account

the asymptotic representation of function Pr(z) (4.23), page 95, we obtain that, for

Passive Tracer Clustering and Diffusion 287

τ  1, the average area of regions where concentration exceeds level ρ decreases in

time according to the law

S(t, ρ)

≈

√

πτρ

−τ/4

(r), (11.51)

while the average tracer mass within these regions

M(t, ρ)

≈ M

−

πτ

−τ/4

(r) (11.52)

monotonously tends to the total mass

drρ

(r).

This is an additional evidence in favor of the above conclusion that tracer particles

tend to join in clusters, i.e., in compact regions of enhanced concentration surrounded

with rareﬁed regions.

We illustrate the dynamics of cluster formation with the example of the initially

uniform distribution of buoyant tracer over the plane, in which case ρ

(r) = ρ

const. In this case, the average speciﬁc area (per unit surface area) of regions within

which ρ(r, t) > ρ is

s(t, ρ|ρ

) =

∞

deρ P(t;eρ|ρ

) = Pr



−τ

/ρ



√

2τ

, (11.53)

where P(t;ρ) is the solution to Eq. (11.44) independent of r (i.e., function (11.47),

and average speciﬁc tracer mass (per unit surface area) within these regions is given

by the expression

m(t, ρ|ρ

)/ρ

∞

eρ deρ P(t;eρ|ρ

) = Pr



(

/ρ

)

√

2τ



. (11.54)

From Eqs. (11.53) and (11.54) it follows that, for sufﬁciently large times, average

speciﬁc area of such regions decreases according to the law

s(t, ρ) ≈

√

πτ

−τ/4

(11.55)

irrespective of ratio ρ/ρ

; at the same time, these regions concentrate almost all tracer

mass

m(t, ρ) ≈ 1 −

√

πτ

−τ/4

. (11.56)

288 Lectures on Dynamics of Stochastic Systems

Nevertheless, the time-dependent behavior of the formation of cluster structure essen-

tially depends on ratio ρ/ρ

. If ρ/ρ

< 1, then s(0, ρ) = 1 and m(0, ρ) = 1 at the

initial instant. Then, in view of the fact that particles of buoyant tracer initially tend to

scatter, there appear small areas within which ρ(r, t) < ρ and which concentrate only

insigniﬁcant portion of the total mass. These regions rapidly grow with time and their

mass ﬂows into cluster region relatively quickly approaching asymptotic expressions

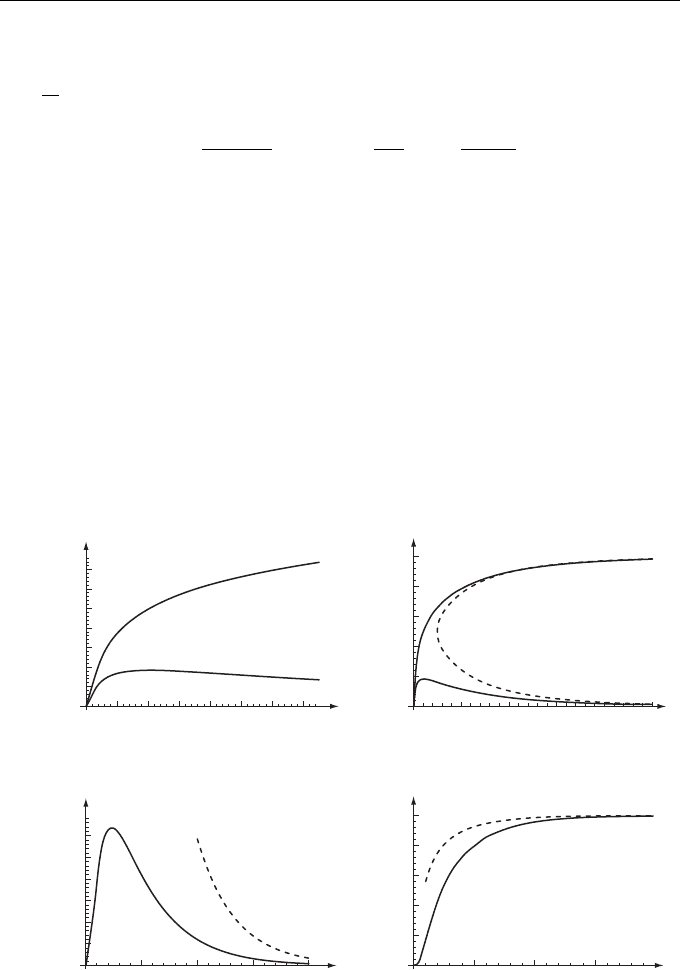
(11.55) and (11.56) (Fig. 11.1).

Note that s(t

∗

, ρ) = 1/2 at instant τ

∗

= ln

(

ρ/ρ

)

In the opposite, more interesting case ρ/ρ

> 1, we have s(0, ρ) =0 and

m(0, ρ) =0 at the initial instant. In view of initial scatter of particles, there appear

small cluster regions within which ρ(r, t) > ρ; these regions remain at ﬁrst almost

invariable in time and intensively absorb a signiﬁcant portion of total mass. With

time, the area of these regions begins to decrease and the mass within them begins

to increase according to asymptotic expressions (11.55) and (11.56) (Fig. 11.2).

As we mentioned earlier, a more detailed description of the tracer concentra-

tion ﬁeld in random velocity ﬁeld requires that spatial gradient p(r, t) = ∇ρ(r, t)

(and, generally, higher-order derivatives) was additionally included in the conside-

ration.

The concentration gradient satisﬁes dynamic equation (1.50), page 28; conse-

quently, the extended indicator function

ϕ(r, t;ρ, p) = δ

(

ρ(r, t) − ρ

)

(

p(r, t) − p

)

for nondivergent velocity ﬁeld satisﬁes Eq. (3.24). Averaging now Eq. (3.24) over an

ensemble of velocity ﬁeld realizations in the approximation of delta-correlated velo-

city ﬁeld, we obtain the equation for the one-point joint probability density of the

concentration and its gradient P(r, t;ρ, p) =

ϕ(r, t;ρ, p)

(this probability density is

m,s

2648

0.8

0.6

0.4

0.2

Figure 11.1 Cluster formation dynamics for ρ/ρ

= 0.5.

Passive Tracer Clustering and Diffusion 289

a function of the space-time point (r, t))

∂

∂t

P(r, t;ρ, p) = D

1P(r, t;ρ, p)

d(d + 2)



(d + 1)

∂

∂p

− 2

∂

∂p



P(r, t;ρ, p).

(11.57)

P(r, 0;ρ, p) = δ

(

(r) − ρ

)

δ( p

(r) − p),

where the diffusion coefﬁcients D

(in r-space) and D

(in p-space) are given by

Eqs. (4.54) and (4.59), pages 107 and 108.

In view of the fact that the random velocity ﬁeld is nondivergent, we can represent

the solution to Eq. (11.57) in the form

P(r, t;ρ, p) =

P(r, t|r

)P( p, t|r

), (11.58)

where P(r, t|r

) and P( p, t|r

) are the corresponding Lagrangian probability densities

of particle position and its gradient. The ﬁrst density is given by Eq. (11.19), and the

(a)

(b)

0.2

0.4

0.6

0.8

0.6

0.4

0.2

246800.4 0.6 0.8

m,s

ττ

0.015

0.01

0.015

5 10 15 5 10 15

0.8

0.6

0.4

0.2

ττ

Figure 11.2 Cluster formation dynamics for (a) ρ/ρ

= 1.5 and (b) ρ/ρ

= 10.

290 Lectures on Dynamics of Stochastic Systems

second one satisﬁes the equation

∂

∂t

P( p, t|r

) =

d(d + 2)



(d + 1)

∂

∂p

− 2

∂

∂p



P( p, t|r

(11.59)

From Eq. (11.59) follows that average tracer concentration gradient is invariant

p(r, t)

= p

As regards the moment functions of the concentration gradient modulus, they satisfy

the equations

∂

∂t



(t|r

)



n(d + n)(d − 1)

d(d + 2)



(t|r

)





(0|r

)



= p

) (11.60)

that follow from (11.59).

Consequently, the concentration gradient modulus in the Lagrangian representation

is the logarithmic-normal quantity whose typical realization curve and all moment

functions increase exponentially in time. In particular, the ﬁrst and second moments

in the two-dimensional case are given by the equalities

|p(t|r

= |p

)|e

t/8



(t|r

)



= p

. (11.61)

In addition, from Eq. (11.57) with allowance for Eq. (4.38) it follows that average

total length of contour ρ(r, t) = ρ = const (remember that we deal with the two-

dimensional case) also exponentially increases in time according to the law

l(t, ρ)

= l

where l

is the initial length of the contour. Remember that, in the case of the nondi-

vergent velocity ﬁeld, the number of contours remains unchanged; the contours cannot

appear and disappear in the medium, they only evolve in time depending on their spa-

tial distribution at the initial instant.

Thus, the initially smooth tracer distribution becomes with time increasingly inho-

mogeneous in space; its spatial gradients sharpen and level lines acquire the fractal

behavior. We observed such a pattern in Fig. 1.1a, page 5 that shows simulated results

(for quite other model of velocity ﬁeld ﬂuctuations). This means that the above general

behavioral characteristics only slightly depend on the ﬂuctuation model.

Above, we studied statistical characteristics of the solution to Eq. (11.3) in the

Lagrangian and Eulerian representations and showed that, if the velocity ﬁeld has

a nonzero potential component, clustering of the Eulerian concentration ﬁeld occurs

with a probability of unity and, under certain conditions, clustering of particles in the

Lagrangian description can take place.

Passive Tracer Clustering and Diffusion 291

Along with dynamic equation (11.13), there is certain interest to the equation



∂

∂t

+ U(r, t)

∂

∂r



ρ(r, t) = 0, ρ(r, 0) = ρ

(r)

that describes transfer of nonconservative tracer. In this case, particle dynamics in

the Lagrangian representation is described by the equation coinciding with Eq. (11.5);

consequently, particles are clustered. However, in the Eulerian representation, no clus-

tering occurs. In this case, as in the case of nondivergent velocity ﬁeld, average number

of contours, average area of regions within which ρ(r, t) > ρ, and average tracer mass

dSρ(r, t) within these regions remain invariant.

Above, we considered the simplest statistical problems on tracer diffusion in ran-

dom velocity ﬁeld in the absence of regular ﬂows and dynamic diffusion. Moreover,

our statistical description used the approximation of random delta-correlated (in time)

ﬁeld. All unaccounted factors begin from a certain time, so that the above results hold

only during the initial stage of diffusion. Furthermore, these factors can give rise to

new physical effects.

11.4 Probabilistic Description of Magnetic Field and

Magnetic Energy in Random Velocity Field

Here, we consider probabilistic description of the magnetic ﬁeld starting from dyna-

mic equation (11.4). As in the case of the density ﬁeld, we will assume that random

component of velocity ﬁeld u(r, t) is the divergent (div u(r, t) 6= 0) Gaussian random

ﬁeld, homogeneous and isotropic in space and stationary and delta-correlated in time.

Introduce the indicator function of magnetic ﬁeld H(r, t),

ϕ(r, t;H) = δ(H(r, t) − H).

It satisﬁes the Liouville equation (3.26), page 76,



∂

∂t

+ u(r, t)

∂

∂r



ϕ(r, t;H) = −

∂

∂H



∂u

(r, t)

∂r

− H

∂u(r, t)

∂r



ϕ(r, t;H)

(11.62)

with the initial condition

ϕ(r, 0;H) = δ(H

(r) − H).

The solution to this equation is a functional of velocity ﬁeld u(r, t), i.e.,

ϕ(r, t;H) = ϕ[r, t;H; u(er, τ )],

where 0 ≤ τ ≤ t. This solution obeys the condition of dynamic causality

δϕ[r, t;H; u(er, τ )]

δu

, t

)

= 0 for t

< 0 and t

> t.

292 Lectures on Dynamics of Stochastic Systems

Moreover, the variational derivative at t

= t − 0 can be represented as

δϕ(r, t;H)

δu

, t − 0)

(r, r

, t;H)ϕ(r, t;H), (11.63)

where operator

(r, r

, t;H) = −δ(r − r

)

∂

∂r

−

∂δ(r − r

)

∂r

∂

∂H

∂δ(r − r

)

∂r

∂

∂H

. (11.64)

The one-point probability density of magnetic ﬁeld is deﬁned as the equality

P(r, t;H) =

ϕ(r, t;H)

Let us average Eq. (11.62) over an ensemble of realizations of ﬁeld {u(r, t)} and

use the Furutsu–Novikov formula (11.14) to split the appeared correlations. Taking

into account equalities (11.63) and (11.64), and Eqs. (4.54), (4.56) and (4.57), page

107, with parameters (4.59), page 108, we obtain then the desired equation



∂

∂t

− D

∂

∂r



P(r, t;H) =



∂

∂H

∂

∂H

+ D

∂

∂H

∂

∂H



P(r, t;H),

(11.65)

where



− 2



− 2D

d(d + 2)

, D

(d + 1)D

+ D

d(d + 2)

are the diffusion coefﬁcients and d is the dimension of space. Note that the one-point

probability density is independent of variable r in the case of homogeneous initial

conditions, and Eq. (11.65) assumes the form

∂

∂t

P(t;H) =



∂

∂H

∂

∂H

+ D

∂

∂H

∂

∂H



P(t;H). (11.66)

Derive now an expression for the one-point correlation of the magnetic ﬁeld



(t)





(r, t)H

(r, t)



in the case of homogeneous initial conditions. Multiplying Eq. (11.66) by H

and H

and integrating over H, we obtain the equation

∂

∂t



(t)



= 2D



(t)



+ 2D

E(t)

Passive Tracer Clustering and Diffusion 293

from which follows the equation for average energy

∂

∂t

E(t)

= 2

d − 1



+ D



E(t)

whose solution is

E(t)

= E

exp



d − 1



+ D





. (11.67)

Now, the solution to the equation in the magnetic ﬁeld correlation is easily found and

has the form



(t)



E(t)



(0)

−



exp



−2

(d + 1)D

+ D

d + 2



. (11.68)

Thus average energy exponentially increases with time, and this process is accom-

panied by isotropization of magnetic ﬁeld, which also goes according to the

exponential law.

Introduce now the indicator function of energy of the magnetic ﬁeld E(r, t) =

(r, t),

ϕ(r, t;E) = δ(E(r, t) − E),

in terms of which probability density of energy P(r, t;E) is deﬁned as the equality

P(r, t;E) =

δ(E(r, t) − E)

δ(H

(r, t) − E)

To derive an equation for this function, one should multiply Eq. (11.65) by function

δ(H

− E) and integrate the result over H. The result will be the equation



∂

∂t

− D

∂

∂r



P(r, t;E) =



∂

∂E

E + D

∂

∂E

∂

∂E



P(r, t;E),

P(r, 0;E) = δ

(

E − E

(r)

)

(11.69)

that coincides with Eq. (8.55), page 207, with the parameters

α = 2

d − 1

d + 2



− D



, D = 4(d − 1)

(

d + 1

)

+ D

d(d + 2)

Parameter α can be both positive and negative. In the context of the one-point charac-

teristics, the change of the sign of α means transition from E to 1/E.

The solution to Eq. (11.69) has the form

P(r, t;E) = exp



∂

∂r



P(r, t;E),

294 Lectures on Dynamics of Stochastic Systems

where function

P(r, t;E) satisﬁes the equation

∂

∂t

P(r, t;E) =



∂

∂E

E + D

∂

∂E

∂

∂E



P(r, t;E),

P(r, 0;E) = δ

(

E − E

(r)

)

Then, dependence of function

P(r, t;E) on parameter r appears only through the initial

value E

(r),

P(r, t;E) ≡

P(t;E|E

(r))

and, consequently, function

P(t;E|E

(r)) is the lognormal probability density of ran-

dom process E(t, |E

(r)) parametrically dependent on r,

P(t;E|E

(r)) =

√

πDt

exp

(

−



αt

(r)



4Dt

)

. (11.70)

Thus, the solution to Eq. (11.69) has the form

P(r, t;E) =

√

πDt

exp



∂

∂r



exp

(

−



αt

(r)



4Dt

)

. (11.71)

Consequences of Eq. (11.69) or Eq. (11.71) are the expressions for spatial integrals

of moment functions



(r, t)



= e

n(nD−α)t

drE

(r),

which are independent of coefﬁcient of diffusion D

in r-space, and, in particular, the

expression for average total energy in the whole space,

E(r, t)

= e

γ t

drE

(r), (11.72)

where parameter

γ = D − α =

2(d − 1)



+ D



. (11.73)

In the case of spatially homogeneous initial distribution of energy E

(r) = E

probability density (11.71) is independent of r and is described by the formula

P(t;E) =

√

πDt

exp

(

−



αt



4Dt

)

. (11.74)

Passive Tracer Clustering and Diffusion 295

Thus, in this case, the one-point statistical characteristics of magnetic energy E(r, t)

are statistically equivalent to statistical characteristics of random process

E(t;α) = exp







−αt +

dτ ξ(τ )







where ξ(t) is the Gaussian process of white noise with the parameters

ξ(t)

= 0,



ξ(t)ξ(t

)



= 2Dδ(t − t

It satisﬁes the stochastic equation

E(t;α) =

{

−α + ξ(t)

}

E(t;α), E(0;α) = E

and its one-point probability density P(t;E, α) is described by the Fokker–Planck

equation

∂

∂t

P(t;E) =



∂

∂E

E + D

∂

∂E

∂

∂E



P(t;E), P(0;E) = δ(E − E

), (11.75)

whose solution is given by Eq. (11.74).

A characteristic feature of distribution (11.74) consists in the appearance of a long

ﬂat tail for Dt  1, which is indicative of an increased role of great peaks of process

E(t;α) in the formation of the one-point statistics. For this distribution, all moments

of magnetic energy are functions exponentially increasing with time



(t)



= E

exp



−2n

d − 1

d + 2



− D



t + 4n

(d − 1)

(

d + 1

)

+ D

d(d + 2)



and, in particular case of n = 1, the speciﬁc average energy is given by Eq. (11.67).

Moreover, quantity

(

E(t)/E

)

= −αt = −2

d − 1

d + 2



− D



so that parameter {−α} is the characteristic Lyapunov exponent [14]. In addition, the

typical realization curve of random process E(t), which determines the behavior of

magnetic energy at arbitrary spatial point in separate realizations, is the exponential

function

∗

(t) = E

−αt

= E

exp



−2

d − 1

d + 2



− D





that can both increase and decrease with time. Indeed, for α < 0 (D

< D

), the typical

realization curve exponentially increases with time, which is evidence of general inc-

rease of magnetic energy at every spatial point. Otherwise, for α > 0 (D

> D