Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

12 Lectures on Dynamics of Stochastic Systems

where Ei(−x) = −

∞

−t

(x > 0) is the integral exponent. Using asymptotic

expansions of function Ei(−x)

Ei(−x) =











ln x (x  1),

−e

−x



1 −



(x  1),

we obtain the asymptotic expansions of quantity





≈

(

1 − 2β ln(1/β),

1/(2β),

β  1,

β  1.

(12.33)

To determine higher moments of quantity W

= |R

, we multiply the ﬁrst equa-

tion in (12.31) by W

and integrate the result over W from 0 to 1. As a result, we

obtain recurrence equation

n+1

− 2(β + n)





+ n

n−1

= 0 (n = 1, 2, . . .). (12.34)

Using this equation, we can recursively calculate all higher moments. For example,

we have for n = 1

= 2(β + 1)

− 1.

The steady-state probability distribution can be obtained not only by limiting pro-

cess L

→ − ∞, but also L →∞. Equation (12.24) was solved numerically for two

values β = 1.0 and β = 0.08 for different initial conditions. Figure 12.3 shows

moments





calculated from the obtained solutions versus dimensionless

layer thickness η =D(L − L

). The curves show that the probability distribution

〈|R

〉, n = 1, 2

1.0

0.735

0.589

0.227

0.109

Figure 12.3 Statistical characteristics of quantity W

= |R

. Curves 1 and 2 show the sec-

ond and ﬁrst moments at β =1, and curves 3 and 4 show the second and ﬁrst moments at

β = 0.08.

Wave Localization in Randomly Layered Media 13

approaches its steady-state behavior relatively rapidly (η ∼ 1.5) for β ≥ 1 and much

slower (η ≥ 5) for strongly stochastic problem with β = 0.08.

Note that, in the problem under consideration, energy ﬂux density and waveﬁeld

intensity at layer boundary x = L can be expressed in terms of the reﬂection coefﬁ-

cient. Consequently, we have for β  1

S(L, L)

= 1 −

= 2β ln(1/β),

I(L, L)

= 1 +

= 2. (12.35)

Taking into account that |T

|=0 in the case of random half-space and using

Eq. (12.4), we obtain that the waveﬁeld energy contained in this half-space

E = D

−∞

dxI(x;L),

has the probability distribution

P(E) = βP(W)

W=(1−βE)

exp



−

(1 − βE)



θ(1 − βE), (12.36)

so that we have, in particular,

= 2 ln(1/β) (12.37)

for β  1.

Note that probability distribution (12.36) allows the limit process to β = 0; as a

result, we obtain the limiting probability density

P(E) =

exp



−



(12.38)

that decays according to the power law for large energies E. The corresponding integ-

ral distribution function has the form

F(E) = exp



−



A consequence of Eq. (12.38) is the fact that all moments of the total wave energy

appear inﬁnite. Nevertheless, the total energy in separate waveﬁeld realizations can be

limited to arbitrary value with a ﬁnite probability.

12.2.2 Source Inside the Layer of a Medium

If the source of plane waves is located inside the medium layer, the waveﬁeld and

energy ﬂux density at the point of source location are given by Eqs. (12.14) and

14 Lectures on Dynamics of Stochastic Systems

(12.16). Quantities R

) and R

) are statistically independent within the frame-

work of the model of the delta-correlated ﬂuctuations of ε

(x), because they satisfy

dynamic equations (12.12) for nonoverlapping space portions. In the case of the inﬁ-

nite space (L

→ −∞, L → ∞), probability densities of quantities R

) and R

)

are given by Eq. (12.32); as a result, average intensity of the waveﬁeld and average

energy ﬂux density at the point of source location are given by the expressions

I(x

)

= 1 +

S(x

)

= 1. (12.39)

The inﬁnite increase of average intensity at the point of source location for β → 0

is evidence of wave energy accumulation in a randomly layered medium; at the same

time, average energy ﬂux density at the point of source location is independent of

medium parameter ﬂuctuations and coincides with energy ﬂux density in free space.

For the source located at perfectly reﬂecting boundary x

= L, we obtain from

Eqs. (12.14) and (12.16)

ref

(L;L)

= 4



1 +



ref

(L;L)

= 4, (12.40)

i.e., average energy ﬂux density of the source located at the reﬂecting boundary is also

independent of medium parameter ﬂuctuations and coincides with energy ﬂux density

in free space.

Note the singularity of the above formulas (12.39), (12.40) for β → 0, which shows

that absorption (even arbitrarily small) serves the regularizing factor in the problem

on the point source.

Using Eq. (12.17), we can obtain the probability distribution of waveﬁeld energy

in the half-space

E = D

−∞

dxI(x;x

In particular, for the source located at reﬂecting boundary, we obtain the expression

ref

(E) =

√

exp

(

−



1 −

βE



)

that allows limiting process β → 0, which is similar to the case of the wave incidence

on the half-space of random medium.

12.2.3 Statistical Energy Localization

In view of Eq. (12.17), the obtained results related to wave ﬁeld at ﬁxed spatial points

(at layer boundaries and at the point of source location) offer a possibility of mak-

ing certain general conclusions about the behavior of the waveﬁeld average intensity

inside the random medium.

Wave Localization in Randomly Layered Media 15

For example, Eq. (12.17) yields the expression for average energy contained in the

half-space (−∞, x

)

= D

−∞

I(x;x

)

S(x

)

. (12.41)

In the case of the plane wave

(

= L

)

incident on the half-space x ≤ L, Eqs. (12.35)

and (12.41) result for β  1 in the expressions

= 2 ln(1/β),

I(L;L

= 2. (12.42)

Consequently, the space segment of length

∼

ln(1/β),

concentrates the most portion of average energy, which means that there occurs the

waveﬁeld statistical localization caused by wave absorption. Note that, in the absence

of medium parameter ﬂuctuations, energy localization occurs on scales about absorp-

tion length Dl

abs

∼

1/β. However, we have l

abs

 l

for β  1. If β → 0, then

→ ∞, and statistical localization of the waveﬁeld disappears in the limiting case

of non-absorptive medium.

In the case of the source in unbounded space, we have

I(x

)

= 1 +

and average energy localization is characterized, as distinct from the foregoing case,

by spatial scale D|x −x

∼

1 for β → 0.

In a similar way, we have for the source located at reﬂecting boundary

ref

(L;L)

= 4



1 +



from which follows that average energy localization is characterized by a half spatial

scale D(L −x)|

∼

1/2 for β → 0.

In the considered problems, waveﬁeld average energy essentially depends on para-

meter β and tends to inﬁnity for β → 0. However, this is the case only for average

quantities. In our further analysis of the waveﬁeld in random medium, we will show

that the ﬁeld is localized in separate realization due to the dynamic localization even

in non-absorptive media.

12.3 Statistical Theory of Radiative Transfer

Now, we dwell on the statistical description of a waveﬁeld in random medium (statisti-

cal theory of radiative transfer). We consider two problems of which the ﬁrst concerns

waves incident on the medium layer and the second concerns waves generated by a

source located in the medium.

16 Lectures on Dynamics of Stochastic Systems

12.3.1 Normal Wave Incidence on the Layer of Random Media

In the general case of absorptive medium, the waveﬁeld is described by the boundary-

value problem (12.1), (12.2). We introduce complex opposite waves

u(x) = u

(x) + u

(x),

u(x) = −ik[u

(x) − u

(x)],

related to the waveﬁeld through the relationships

(

)



1 +



(

)

, u

(

)

= 1,

(

)



1 −



(

)

, u

(

)

= 0,

so that the boundary-value problem (12.1), (12.2) can be rewritten in the form



+ ik



(

)

= −

ε(x)

[

(

)

+ u

(

)

]

, u

(

)

= 1,



− ik



(

)

= −

ε(x)

[

(

)

+ u

(

)

]

, u

(

)

= 0.

The waveﬁeld as a function of parameter L satisﬁes imbedding equation (12.6). It

is obvious that the opposite waves will also satisfy Eq. (12.6), but with different initial

conditions:

∂

∂L

(x;L) = ik



1 +

ε(L)

(

1 + R

)



(x;L), u

(x;x) = 1,

∂

∂L

(x;L) = ik



1 +

ε(L)

(

1 + R

)



(x;L), u

(x;x) = R

where reﬂection coefﬁcient R

satisﬁes Eq. (12.5).

Introduce now opposite wave intensities

(x;L) = |u

(x;L)|

and W

(x;L) = |u

(x;L)|

They satisfy the equations

∂

∂L

(x;L) = −kγ W

(x;L) +

ε(L)



− R

∗



(x;L),

∂

∂L

(x;L) = −kγ W

(x;L) +

ε(L)



− R

∗



(x;L),

(x;x) = 1, W

(x;x) = |R

(12.43)

Wave Localization in Randomly Layered Media 17

Quantity W

=|R

appeared in the initial condition of Eqs. (12.43) satisﬁes

Eq. (12.7), page 327, or the equation

= −2kγ W

−

(L)



− R

∗



(

1 − W

)

, W

= 0. (12.44)

In Eqs. (12.43) and (12.44), we omitted dissipative terms producing no contribution

in accumulated effects.

As earlier, we will assume that ε

(x) is the Gaussian delta-correlated process with

correlation function (12.18). In view of the fact that Eqs. (12.43), (12.44) are the ﬁrst-

order equations with initial conditions, we can use the standard procedure of deriving

the Fokker–Planck equation for the joint probability density of quantities W

(x;L),

(x;L), and W

P(x;L;W

, W

, W) =

δ(W

(x;L) − W

)δ(W

(x;L) − W

)δ(W

− W)

As a result, we obtain the Fokker–Planck equation

∂

∂L

P(x;L;W

, W

, W)

= kγ



∂

∂W

∂

∂W

+ 2

∂

∂W



P(x;L;W

, W

, W)

+ D



∂

∂W

∂

∂W

−

∂

∂W

(

1 − W

)



P(x;L;W

, W

, W)

+ D



∂

∂W

∂

∂W

−

∂

∂W

(

1 − W

)



WP(x;L;W

, W

) (12.45)

with the initial condition

P(x;x;W

, W

, W) = δ(W

− 1)δ(W

− W)P(x;W),

where function P(L;W) is the probability density of reﬂection coefﬁcient squared

modulus W

, which satisﬁes Eq. (12.24). As earlier, the diffusion coefﬁcient in

Eq. (12.45) is D =k

/2. Deriving this equation, we used an additional averaging

over fast oscillations (u(x) ∼ e

±ikx

) that appear in the solution of the problem at ε = 0.

In view of the fact that Eqs. (12.43) are linear in W

(x;L), we can introduce the

generating function of moments of opposite wave intensities

Q(x;L;µ, λ, W) =

µ−λ

P(x;L;W

, W

, W), (12.46)

18 Lectures on Dynamics of Stochastic Systems

which satisﬁes the simpler equation

∂

∂L

Q(x;L;µ, λ, W) = −kγ



µ − 2

∂

∂W



Q(x;L;µ, λ, W)

− D



µ +

∂

∂W

(

1 − W

)



Q(x;L;µ, λ, W)

+ D



µ −

∂

∂W

(

1 − W

)



WQ(x;L;µ, λ, W) (12.47)

with the initial condition

Q(x;x;µ, λ, W) = W

P(x;W).

In terms of function Q(x;L;µ, λ, W), we can determine the moment functions of

opposite wave intensities by the formula

µ−λ

(x;L)W

(x;L)

dWQ(x;L;µ, λ, W). (12.48)

Equation (12.47) describes statistics of the waveﬁeld in medium layer L

≤ x ≤ L.

In particular, at x = L

, it describes the transmission coefﬁcient of the wave.

In the limiting case of the half-space (L

→ −∞), Eq. (12.47) grades into the

equation

∂

∂ξ

Q(ξ;µ, λ, W) = −β



µ − 2

∂

∂W



Q(ξ;µ, λ, W)

−



µ +

∂

∂W

(

1 − W

)



Q(ξ;µ, λ, W)



µ −

∂

∂W

(

1 − W

)



WQ(ξ;µ, λ, W) (12.49)

with the initial condition

Q(0;µ, λ, W) = W

P(W),

where ξ = D(L − x) > 0 is the dimensionless distance, and steady-state (indepen-

dent of L) probability density of the reﬂection coefﬁcient modulus P(W) is given by

Eq. (12.32). In this case, Eq. (12.48) assumes the form

µ−λ

(ξ)W

(ξ)

dWQ(ξ;µ, λ, W). (12.50)

Further discussion will be more convenient if we consider separately the cases of

absorptive (dissipative) and non-absorptive (nondissipative) random medium.

Wave Localization in Randomly Layered Media 19

Nondissipative Medium (Stochastic Wave Parametric Resonance and Dynamic

Wave Localization)

Let us now discuss the equations for moments of opposite wave intensities in the

non-absorptive medium, i.e., to Eq. (12.49) at β = 0 in the limit of the half-space

→ −∞). In this case, W

= 1 with a probability equal to unity, and the solution

to Eq. (12.49) has the form

Q(x, L;µ, λ, W) = δ(W − 1)e

Dλ(λ−1)(L−x)

so that

λ−µ

(x;L)W

(x;L)

= e

Dλ(λ−1)(L−x)

In view of arbitrariness of parameters λ and µ, this means that

(x;L) = W

(x;L) = W(x;L)

with a probability equal to unity, and quantity W(x;L) has the lognormal probability

density. In addition, the mean value of this quantity is equal to unity, and its higher

moments beginning from the second one exponentially increase with the distance in

the medium

W(x;L)

= 1,



(x;L)



= e

Dn(n−1)(L−x)

, n = 2, 3, . . . .

Note that waveﬁeld intensity I(x;L) has in this case the form

I(x;L) = 2W(x;L)

(

1 + cos φ

)

, (12.51)

where φ

is the phase of the reﬂection coefﬁcient.

In view of the lognormal probability distribution, the typical realization curve of

function W(x, L) is, according to Eq. (4.61), page 109, the function exponentially

decaying with distance in the medium

∗

(x, L) = e

−D(L−x)

, (12.52)

and this function is related to the Lyapunov exponent.

Moreover, realizations of function W(x, L) satisfy with a probability of 1/2 the

inequality

W(x, L) < 4e

−D(L−x)/2

within the whole half-space.

In physics of disordered systems, the exponential decay of typical realization curve

(12.52) with increasing ξ = D(L−x) is usually identiﬁed with the property of dynamic

localization, and quantity

loc

20 Lectures on Dynamics of Stochastic Systems

is usually called the localization length. Here,

−1

loc

= −

∂

∂L

κ(x;L)

where

κ(x;L) = ln W(x;L).

Physically, the lognormal property of the waveﬁeld intensity W(x;L) implies the

existence of large spikes relative typical realization curve (12.52) towards both large

and small intensities. This result agrees with the example of simulations given in

Lecture I (see Fig. 1.10, page 20). However, these spikes of intensity contain only

small portion of energy, because random area below curve W(x;L),

S(L) = D

−∞

dxW(x;L),

has, in accordance with the lognormal probability distribution attribute, the steady-

state (independent of L) probability density

P(S) =

exp



−



that coincides with the distribution of total energy of the wave ﬁeld in the half-space

(12.38) if we set E = 2S. This means that the term dependent on fast phase oscillations

of reﬂection coefﬁcient in Eq. (12.51) only slightly contributes to total energy.

Thus, the knowledge of the one-point probability density provides an insight into

the evolution of separate realizations of waveﬁeld intensity in the whole space and

allows us to estimate the parameters of this evolution in terms of statistical characte-

ristics of ﬂuctuating medium.

Dissipative Medium

In the presence of a ﬁnite (even arbitrary small) absorption in the medium occupying

the half-space, the exponential growth of moment functions must cease and give place

to attenuation. If β  1 (i.e., if the effect of absorption is great in comparison with

the effect of diffusion), then

P(W) = 2βe

−2βW

and, as can be easily seen from Eq. (12.49), opposite wave intensities W

(x;L) and

(x;L) appear statistically independent, i.e., uncorrelated. In this case,

(ξ)

= exp



−βξ



1 +



(ξ)

2β

exp



−βξ



1 +



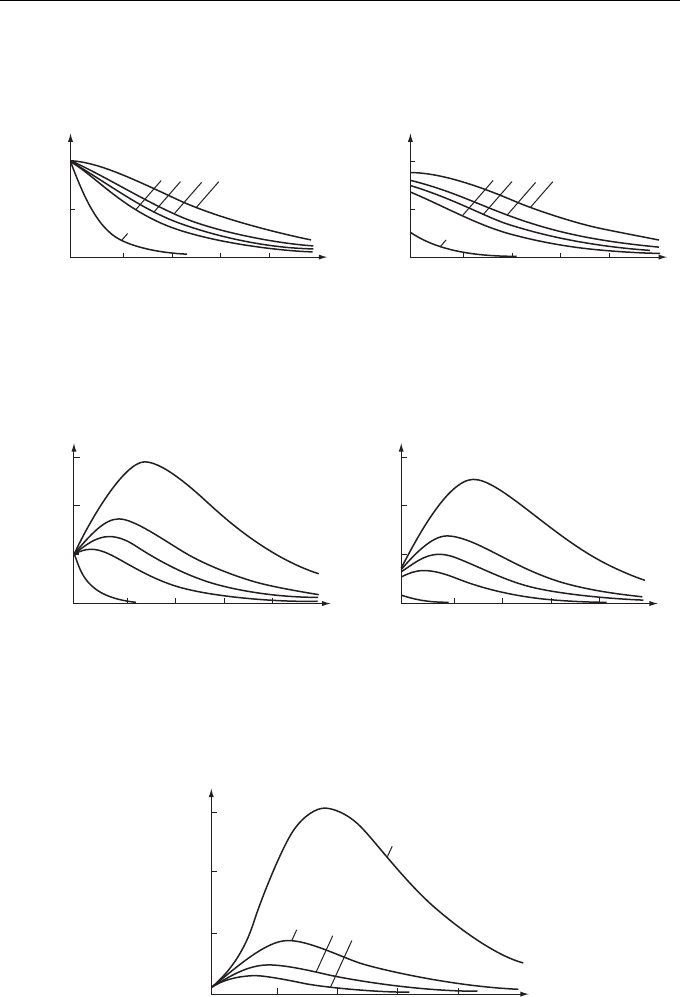
Wave Localization in Randomly Layered Media 21

Figures 12.4–12.7 show the examples of moment functions of random processes

obtained by numerical solution of Eq. (12.49) and calculation of quadrature (12.50)

for different values of parameter β. Different ﬁgures mark the curves corresponding

0.5

1.0

2345

1234 1234

23 45

(a) (b)

ξξ

〈W

〉

0.5

1.0

〈W

〉

Figure 12.4 Distribution of waveﬁeld average intensity along the medium; (a) the transmitted

wave and (b) the reﬂected wave. Curves 1 to 5 correspond to parameter β = 1, 0.1, 0.06, 0.04

and 0.02, respectively.

〈W

〉

〈W

〉

(a)

(b)

Figure 12.5 Distribution of the second moment of waveﬁeld intensity along the medium;

(a) the transmitted wave and (b) the reﬂected wave. Curves 1 to 5 correspond to parameter

β = 1, 0.1, 0.06, 0.04 and 0.02, respectively.

〈W

〉

Figure 12.6 Distribution of the third moment of transmitted wave intensity. Curves 1 to 5

correspond to parameter β = 1, 0.1, 0.06, 0.04 and 0.02, respectively.