Klyatskin V.I. Lectures on Dynamics of Stochastic Systems

Подождите немного. Документ загружается.

22 Lectures on Dynamics of Stochastic Systems

234

〈ΔW

ΔW

〉

Figure 12.7 Correlation between the intensities of transmitted and reﬂected waves. Curves 1

to 5 correspond to parameter β = 1, 0.1, 0.06, 0.04 and 0.02, respectively.

to different values of parameter β. Figure 12.4 shows average intensities of the trans-

mitted and reﬂected waves. The curves monotonically decrease with increasing ξ.

Figure 12.5 shows the corresponding curves for second moments. We see that



(0)



= 1 and



(0)







at ξ = 0. For β < 1, the curves as functions

of ξ become nonmonotonic; the moments ﬁrst increase, then pass the maximum, and

ﬁnally monotonically decay. With decreasing parameter β, the position of the maxi-

mum moves to the right and the maximum value increases.

The fact that moments of intensity behave in the layer as exponentially increasing

functions is evidence of the phenomenon of stochastic wave parametric resonance,

which is similar to the ordinary parametric resonance. The only difference con-

sists in the fact that values of intensity moments at layer boundary are asymptoti-

cally predetermined; as a result, the waveﬁeld intensity exponentially increases inside

the layer and its maximum occurs inside the layer. Figure 12.6 shows the similar

curves for the third moment



(ξ)



, and Fig. 12.7 shows curves for mutual corre-

lation of intensities of the transmitted and reﬂected waves

(ξ)1W

(ξ)

(here,

(ξ) =W

(ξ) −

(ξ)

). For β ≥1, this correlation disappears. For β < 1, the

correlation is strong, and wave division into opposite waves appears physically sense-

less, but mathematically useful technique. For β ≥ 1, such a division is justiﬁed in

view of the lack of mutual correlation.

As was shown earlier, in the case of the half-space of random medium with β = 0,

all waveﬁeld moments beginning from the second one exponentially increase with the

distance the wave travels in the medium. It is clear, that problem solution for small

β (β 1) must show the singular behavior in β in order to vanish the solution for

sufﬁciently long distances.

One can show that, in asymptotic limit β 1, intensities of the opposite waves

are equal with a probability equal to unity, and the solution for small distances from

the boundary coincides with the solution corresponding to the stochastic parametric

resonance.

For sufﬁciently great distances ξ, namely

ξ  4



n −







Wave Localization in Randomly Layered Media 23

quantities

(ξ)

are characterized by the universal spatial localization behavior [67]



(ξ)



∼

n−1/2





√

−ξ/4

which coincides to a numerical factor with the asymptotic behavior of moments of the

transmission coefﬁcient of a wave passed through the layer of thickness ξ in the case

β = 0.

Thus, there are three regions where moments of opposite wave intensities show

essentially different behavior. In the ﬁrst region (it corresponds to the stochastic

wave parametric resonance), the moments exponentially increase with the distance

in medium and wave absorption plays only insigniﬁcant role. In the second region,

absorption plays the most important role, because absorption ceases the exponential

growth of moments. In the third region, the decrease of moment functions of opposite

wave intensities is independent of absorption. The boundaries of these regions depend

on parameter β and tend to inﬁnity for β → 0.

12.3.2 Plane Wave Source Located in Random Medium

Consider now the asymptotic solution of the problem on the plane wave source in

inﬁnite space (L

→ −∞, L →∞) under the condition β →0. In this case, it appears

convenient to calculate average waveﬁeld intensity in region x < x

using relationships

(12.15) and (12.16)

I(x;x

)

∂

∂x

S(x;x

)

∂

∂x

ψ(x;x

)

where quantity

ψ(x;x

) = exp







−βD

dξ

|1 + R

1 − |R







satisﬁes, as a function of parameter x

, the stochastic equation

∂

∂x

ψ(x;x

) = −βD

|1 + R

1 − |R

ψ(x;x

), ψ(x;x) = 1.

Introduce function

ϕ(x;x

;u) = ψ(x;x

)δ(u

− u), (12.53)

where function u

= (1 + W

)/(1 − W

) satisﬁes the stochastic system of equa-

tions (12.25). Differentiating Eq. (12.53) with respect to x

, we obtain the stochastic

24 Lectures on Dynamics of Stochastic Systems

equation

∂

∂x

ϕ(x;x

;u) = −βD

u +

− 1 cos φ

ϕ(x;x

;u)

+ βD

∂

∂u

n

− 1



ϕ(x;x

;u)

− kε

)

∂

∂u

− 1 sin φ

ϕ(x;x

;u)

. (12.54)

Average now Eq. (12.54) over an ensemble of realizations of random process ε

)

assuming it, as earlier, the Gaussian process delta-correlated in x

. Using the Furutsu–

Novikov formula (12.22), page 331, the following expression for the variational

derivatives

δϕ(x;x

;u)

δε

)

= −k

∂

∂u

− 1 sin φ

ϕ(x;x

;u)

δφ

δε

)

= k





1 +

− 1





cos φ

and additionally averaging over fast oscillations (over the phase of reﬂection coefﬁ-

cient), we obtain that function

8(ξ;u) =

ϕ(x;x

;u)



ψ(x;x

)δ(u

− u)



where ξ = D|x − x

|, satisﬁes the equation

∂

∂ξ

8(ξ;u) = −βu8(ξ ;u) + β

∂

∂u



− 1



8(ξ;u)

∂

∂u



− 1



∂

∂u

8(ξ;u) (12.55)

with the initial condition

8(0;u) = P(u) = βe

−β(u−1)

The average intensity can now be represented in the form

I(x;x

)

= −

∂

∂ξ

∞

du8(ξ;u) = β

∞

duu8(ξ;u).

Equation (12.55) allows limiting process β → 0. As a result, we obtain a simpler

equation

∂

∂ξ

8(ξ;u) = −u

8(ξ;u) +

∂

∂u

8(ξ;u) +

∂

∂u

∂

∂u

8(ξ;u),

8(0;u) = e

−u

(12.56)

Wave Localization in Randomly Layered Media 25

Consequently, localization of average intensity in space is described by the quadrature

loc

(ξ) =

∞

duu

8(ξ;u),

where

loc

(ξ) = lim

β→0

I(x;x

)

= lim

β→0

I(x;x

)

I(x

)

Thus, the average intensity of the waveﬁeld generated by the point source has for

β  1 the following asymptotic behavior

I(x;x

)

loc

(ξ).

Equation (12.56) can be easily solved with the use of the Kontorovich–Lebedev

transform; as a result, we obtain the expression for the localization curve

loc

(ξ) = 2π

∞

dτ τ





sinh(πτ )

cosh

(πτ )

−





. (12.57)

For small distances ξ , the localization curve decays according to relatively

fast law

loc

(ξ) ≈ e

−2ξ

. (12.58)

For great distances ξ (namely, for ξ  π

), it decays signiﬁcantly slower, according

to the universal law

loc

(ξ) ≈

√

−ξ/4

, (12.59)

but for all that

∞

dξ8

loc

(ξ) = 1.

Function (12.57) is given in Fig. 12.8, where asymptotic curves (12.58) and (12.59)

are also shown for comparison purposes.

A similar situation occurs in the case of the plane wave source located at the reﬂect-

ing boundary.

26 Lectures on Dynamics of Stochastic Systems

1 2

0.2

0.4

0.6

0.8

loc

(ξ)

Figure 12.8 Localization curve for a source in inﬁnite space (12.57) (curve a). Curves b and

c correspond to asymptotic expressions for small and large distances from the source.

In this case, we obtain the expression

lim

β→0

ref

(x;L)

ref

(L;L)

loc

(ξ), ξ = D(L − x). (12.60)

12.4 Numerical Simulation

The above theory rests on two simpliﬁcations – on using the delta-correlated approxi-

mation of function ε

(x) (or the diffusion approximation) and eliminating slow (within

the scale of a wavelength) variations of statistical characteristics by averaging over

fast oscillations. Averaging over fast oscillations is validated only for statistical cha-

racteristics of the reﬂection coefﬁcient in the case of random medium occupying a

half-space. For statistical characteristics of the waveﬁeld intensity in medium, the cor-

responding validation appears very difﬁcult if at all possible (this method is merely

physical than mathematical). Numerical simulation of the exact problem offers a pos-

sibility of both verifying these simpliﬁcations and obtaining the results concerning

more difﬁcult situations for which no analytic results exists.

In principle, such numerical simulation could be performed by way of multiply

solving the problem for different realizations of medium parameters followed by ave-

raging the obtained solutions over an ensemble of realizations. However, such an

approach is not very practicable because it requires a vast body of realizations of

medium parameters. Moreover, it is unsuitable for real physical problems, such as

wave propagation in Earth’s atmosphere and ocean, where only a single realization

is usually available. A more practicable approach is based on the ergodic property

of boundary-value problem solutions with respect to the displacement of the problem

along the single realization of function ε

(x) deﬁned along the half-axis (L

, ∞) (see

Fig. 12.9).

This approach assumes that statistical characteristics are calculated by the formula

F(L

;x, x

;L)

= lim

δ→∞

;x, x

;L),

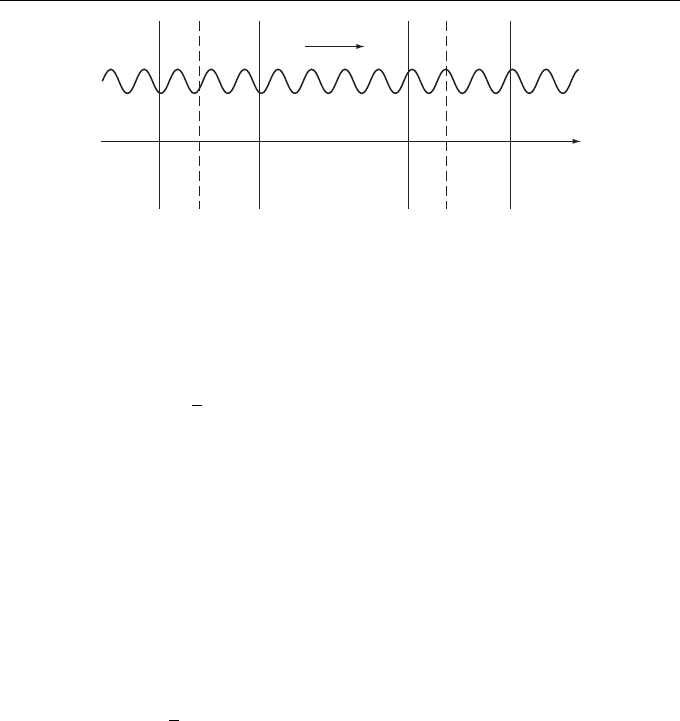
Wave Localization in Randomly Layered Media 27

+Δ

x +Δ L +Δ

(x)

Figure 12.9 Averaging over parameter 1 by the procedure based on ergodicity of imbedding

equations for a half-space of random medium.

where

;x, x

;L) =

d1F(L

+ 1;x + 1, x

+ 1;L + 1).

In the limit of a half-space (L

→ −∞), statistical characteristics are indepen-

dent of L

, and, consequently, the problem have ergodic property with respect to the

position of the right-hand layer boundary L (simultaneously, parameter L is the vari-

able of the imbedding method), because this position is identiﬁed in this case with

the displacement parameter. As a result, having solved the imbedding equation for the

sole realization of medium parameters, we simultaneously obtain all desired statistical

characteristics of this solution by using the obvious formula

F(x, x

;L)

dξF

(

ξ, ξ + x

− x;ξ + (L − x

) + (x

− x)

)

for sufﬁciently large interval (0, δ). This approach offers a possibility of calcu-

lating even the wave statistical characteristics that cannot be obtained within the

framework of current statistical theory, and this calculation requires no additional

simpliﬁcations.

In the case of the layer of ﬁnite thickness, the problem is not ergodic with respect

to parameter L. However, the corresponding solution can be expressed in terms of two

independent solutions of the problem on the half-space and, consequently, it can be

reduced to the case ergodic with respect to L.

As an example let us discuss the case of the point source located at reﬂect-

ing boundary x

=L with boundary condition dG(x;x

;L)/dx|

x=L

=0. Figure 12.10

shows the quantity

ref

(x;x

)

simulated with β =0.08 and k/D =25. In region

ξ =D(L−x) < 0.3, one can see oscillations of period T =0.13. For larger ξ , simulated

results agree well with localization curve (12.60).

28 Lectures on Dynamics of Stochastic Systems

2.0

1.5

1.0

0.5

0.1

0.2

0.3

0.4

〈I

ref

(x ;L)〉

〈I

ref

(L;L)〉

Figure 12.10 Curve 1 shows the localization curve (12.57) and circles 2 show the simulated

result.

Problems

Problem 12.1

Derive the probability distribution of the reﬂection coefﬁcient phase in the prob-

lem on a plane wave incident on the half-space of nondissipative medium (see,

for example, [67])

Instruction In this case, reﬂection coefﬁcient has the form R

= exp{iφ

}, where

phase φ

satisﬁes the imbedding equation following from Eq. (12.19)

= 2k + kε

(L)

(

1 + cos φ

)

, φ

= 0. (12.61)

The solution to Eq. (12.61) is deﬁned over the whole axis φ

(−∞, ∞).

A more practicable characteristic is the probability distribution in interval

(−π, π), which must be independent of L in the case of the half-space. To obtain

such a distribution, it is convenient to consider singular function z

= tan

(

)

instead of phase φ

. The corresponding dynamic equation has the form

= k



1 + z



+ kε

(L), z

= 0.

Solution Assuming that ε

(L) is the Gaussian delta-correlated random func-

tion with the parameters given in Eq. (12.18)), we obtain that probability den-

sity P(z, L) =

δ(z

− z)

deﬁned over the whole axis (−∞, ∞) satisﬁes the

Fokker–Planck equation

∂

∂L

P(z, L) = −k

∂

∂z



1 + z



P(z, L) + 2D

∂

∂z

P(z, L).

For the random half-space (L

→ −∞), the steady-state (independent of L) solu-

tion to the Fokker–Planck equation can be obtained as P(z) = lim

→−∞

P(z, L)

Wave Localization in Randomly Layered Media 29

and satisﬁes the equation

−κ



1 + z



P(z) +

P(z) = 0, (12.62)

where

κ =

, D =

The solution to Eq. (12.62) corresponding to constant probability ﬂux density

has the form

P(z) = J(κ)

∞

dξ exp



−κξ



1 +

+ z(z + ξ )



where J(κ) is the steady-state probability ﬂux density,

−1

(κ) =

∞

−1/2

dξ exp



−κ



ξ +



The corresponding probability distribution of the wave phase over interval

(−π, π) is as follows

P(φ) =

1 + z

P(z)



z=tan(φ/2)

For κ  1, we have asymptotically

P(z) =

π(1 + z

)

which corresponds to the uniform distribution of the reﬂection coefﬁcient phase

P(φ) =

2π

, −π < φ < π.

In the opposite limiting case κ  1, we obtain

P(z) = κ

1/3





1/6

√

π0(1/6)



κz



where 0(µ, z) is the incomplete gamma function. From this expression follows

that

P(z) = κ

1/3





1/6

√

π0(1/6)



κz



2/3

for κ|z|

 3 and |z| → ∞.

30 Lectures on Dynamics of Stochastic Systems

Problem 12.2

In the diffusion approximation, derive the equation for the reﬂection coefﬁcient

probability density.

Solution The equation for the reﬂection coefﬁcient probability density has the

form of the Fokker–Planck equation (12.22) with the diffusion coefﬁcient

D(k, l

) =

∞

−∞

dξB

(ξ) cos

(

2kξ

)

(2k),

where 8

(q) =

∞

−∞

dξB

(ξ)e

iqξ

is the spectral function of random process

(x). Applicability range of this equation is given by the conditions

D(k, l

 1, α =

D(k, l

)

 1.

Problem 12.3

Derive the equation for the reﬂection coefﬁcient probability density in the case

of matched boundary.

Instruction In the case of matched boundary, reﬂection coefﬁcient satisﬁes the

Riccati equation

= 2ikR

− kγ R

ξ(L)



1 − R



, R

= 0,

where ξ(L) = ε

(L). For the Gaussian process with correlation function B

(x),

random process ξ(x) is also the Gaussian process with correlation function

(x −x

) =



ξ(x)ξ(x

)



= −

∂

∂x

(x −x

Solution The equation for the reﬂection coefﬁcient probability density has the

form of the Fokker–Planck equation (12.22) with the diffusion coefﬁcient

D(k, l

) =

(2k).

Lecture 13

Caustic Structure of Waveﬁeld

in Random Media

Fluctuations of waveﬁeld propagating in a medium with random large-scale (in

comparison with wavelength) inhomogeneities rapidly grow with distance because

of multiple forward scattering. Perturbation theory in any version fails from a cer-

tain distance (the boundary of the region of strong ﬂuctuation). Strong ﬂuctuations of

intensity can appear in radiowaves propagating through the ionosphere, solar corona,

or interstellar medium, in occultation experiments on transilluminating planet’s atmo-

spheres when planets shadow natural or artiﬁcial radiation sources, and in a number

of other cases.

The current state of the theory of wave propagation in random media can be found

in monographs and reviews [2, 68, 69]. Below, we will follow works [68, 69] to

describe wave propagation in random media within the framework of the parabolic

equation of quasi-optics and delta-correlated approximation of medium parameter

ﬂuctuations and discuss the applicability of such an approach.

13.1 Input Stochastic Equations and Their Implications

We will describe the propagation of a monochromatic wave in the medium with

large-scale inhomogeneities in terms of the complex scalar parabolic equation (1.89),

page 39,

∂

∂x

u(x, R) =

u(x, R) + i

ε(x, R)u(x, R), (13.1)

where function ε(x, R) is the ﬂuctuating portion (deviation from unity) of dielectric

permittivity, x-axis is directed along the initial direction of wave propagation, and vec-

tor R denotes the coordinates in the transverse plane. The initial condition to Eq. (13.1)

is the condition

u(0, R) = u

(R). (13.2)

Because Eq. (13.1) is the ﬁrst-order equation in x and satisﬁes initial condition

(13.2) at x = 0, it possesses the causality property with respect to the x-coordinate (it

Lectures on Dynamics of Stochastic Systems. DOI: 10.1016/B978-0-12-384966-3.00013-1