Klyatskin V.I. Lectures on Dynamics of Stochastic Systems
Подождите немного. Документ загружается.


376 Lectures on Dynamics of Stochastic Systems
expression
I
n
(x, R)
≈ n!
k
2πx
2n
Z
···
Z
A
1
dv
1
. . . dv
2n
× exp
ik
2x
2n
X
j=1
(−1)
j+1
v
2
j
−
k
2
1x
4
n
X
l=1
D
(
v
2l−1
− v
2l
)
×
1 +
k
2
1x
8
2n
X
j,l=1
0
(−1)
j+l+1
D
v
j
− v
l
+ ···
. (13.73)
Here, the prime of the sum sign means that this sum excludes the terms kept in the
exponent. Because the integrand is negligible outside region A
1
, we can extend the
region of integration in Eq. (13.73) to the whole space. Then the multiple integral in
Eq. (13.73) can be calculated in analytic form, and we obtain for
h
I
n
(x, R)
i
the formula
I
n
(x, R)
= n!
1 + n(n −1)
β
2
(x) − 1
4
+ ···
, (13.74)
where quantity β
2
(x) is given by Eq. (13.69). We discuss this formula a little later,
after considering wave propagation in continuous random medium, which yields a
very similar result.
Continuous Medium
Consider now the asymptotic behavior of higher moment functions of the wavefield
M
nn
(x, R
1
, . . . , R
2n
) propagating in random medium. The formal solution to this prob-
lem is given by Eqs. (13.60) and (13.61). They differ from the phase screen formulas
only by the fact that ordinary integrals are replaced with path integrals.
We consider first quantity
I(x, R
0
)I(x, R
00
)
= M
22
(x, R
1
, . . . , R
4
)
|
R
1
=R
2
=R
0
, R
3
=R
4
=R
00
.
In the case of the plane wave
(
u
0
(R) = 1
)
, we can use (13.61) and introduce new
variables similar to those for the phase screen to obtain
I(x, R
0
)I(x, R
00
)
= exp
i
k
x
Z
0
dξ
δ
2
δv
1
(ξ)δv
2
(ξ)
× exp
−
k
2
4
x
Z
0
dx
0
2D
ρ +
x
Z
x
0
dξv
1
(ξ)
+ 2D
x
Z
x
0
dξv
2
(ξ)

Caustic Structure of Wavefield in Random Media 377
− D
ρ +
x
Z
x
0
dξ
[
v
1
(ξ) + v
2
(ξ)
]
− D
ρ +
x
Z
x
0
dξ
[
v
1
(ξ) − v
2
(ξ)
]
v
i
=0
,
(13.75)
where ρ = R
0
− R
00
.
Using Eq. (13.60), formula (13.75) can be represented in the form of the path integ-
ral; however, we will use here the operator representation. As in the case of the phase
screen, we can represent
I(x, R
0
)I(x, R
00
)
for x → ∞ in the form
B
I
(x, ρ) =
I(x, R
0
)I(x, R
00
)
− 1 = B
(1)
I
(x, ρ) + B
(2)
I
(x, ρ) + B
(3)
I
(x, ρ),
(13.76)
where
B
(1)
I
(x, ρ) = exp
−
k
2
x
2
D
(
ρ
)
,
B
(2)
I
(x, ρ) = π k
2
x
Z
0
dx
0
Z
dq8
ε
(q)
1 − cos
q
2
k
(x −x
0
)
× exp
iqρ −
k
2
x
0
2
D
q
k
(x −x
0
)
−
k
2
2
x
Z
x
0
dx
0
D
q
k
(x −x
00
)
,
B
(3)
I
(x, ρ) = π k
2
x
Z
0
dx
0
Z
dq8
ε
(q)
1 − cos
qρ −
q
2
k
(x −x
0
)
× exp
−
k
2
x
0
2
D
ρ −
q
k
(x −x
0
)
−
k
2
2
x
Z
x
0
dx
0
D
ρ −
q
k
(x −x
00
)
.
Setting ρ = 0 and taking into account only the first term of the expansion of function
1 − cos
q
2
k
(x −x
0
),
we obtain that intensity variance
β
2
(x) =
D
I
2
(x, R)
E
− 1 = B
I
(x, 0) − 1

378 Lectures on Dynamics of Stochastic Systems
is given by the formula similar to Eq. (13.68)
β
2
(x) = 1 + π
x
Z
0
dx
0
(x −x
0
)
Z
dq q
4
8
ε
(q)
× exp
−
k
2
x
0
2
D
q
k
(x −x
0
)
−
k
2
2
x
Z
x
0
dx
0
D
q
k
(x −x
00
)
+ ··· .
(13.77)
If we deal with the turbulent medium, then Eq. (13.77) yields
β
2
(x) = 1 + 0.861
(
β
0
(x)
)
−2/5
, (13.78)
where β
0
(x) is the wavefield intensity variance calculated in the first approximation of
Rytov’s smooth perturbation method (13.42).
Expression (13.77) remains valid also in the case when functions 8
ε
(q) and D
(
ρ
)
slowly vary with x. In this case, we can easily reduce Eq. (13.77) to Eq. (13.68) by
setting 8
ε
(q) = 0 outside layer 0 ≤ x
0
≤ 1x x.
Concerning correlation function B
I
(x, ρ), we note that the main term B
(1)
I
(x, ρ)
in Eq. (13.76) is the squared modulus of the second-order coherence function
(see, e.g., [77]).
Now, we turn to the higher moment functions
h
I
n
(x, R)
i
= 0
2n
(x, 0). Similarly to
the case of the phase screen, one can easily obtain that this moment of the wavefield
in continuous medium is represented in the form of the expansion
I
n
(x, R)
= n!
1 + n(n −1)
β
2
(x) − 1
4
+ ···
, (13.79)
which coincides with expansion (13.74) for the phase screen, excluding the fact that
parameter β
2
(x) is given by different formulas in these cases.
Formula (13.79) specifies two first terms of the asymptotic expansion of function
h
I
n
(x, R)
i
for β
2
0
(x) → ∞. Because β
2
(x) → 1 for β
0
(x) → ∞, the second term
in Eq. (13.79) is small in comparison with the first one for sufficiently great β
0
(x).
Expression (13.79) makes sense only if
n(n − 1)
β
2
(x) − 1
4
1. (13.80)
However, we can always select numbers n for which condition (13.80) will be violated
for a fixed β
0
(x). This means that Eq. (13.79) holds only for moderate n. It should be
noted additionally that the moment can approach the asymptotic behavior (13.79) for
β
0
(x) → ∞ fairly slowly.

Caustic Structure of Wavefield in Random Media 379
Formula (13.79) yields the singular probability density of intensity. To avoid the
singularities, we can approximate this formula by the expression (see, e.g., [78])
I
n
(x, R)
= n! exp
n(n − 1)
β
2
(x) − 1
4
, (13.81)
which yields the probability density (see, e.g., [78, 79])
P(x, I) =
1
√
π
(
β(x) − 1
)
∞
Z
0
dz exp
−zI −
ln z −
β(x) − 1
4
2
β(x) − 1
. (13.82)
Note that probability distribution (13.82) is not applicable in a narrow region I ∼ 0
(the width of this region the narrower the greater parameter β
0
(x)). This follows from
the fact that Eq. (13.82) yields infinite values for the moments of inverse intensity
1/I(x, R). Nevertheless, moments
h
1/I
n
(x, R)
i
are finite for any finite-valued parame-
ter β
2
0
(x) (arbitrarily great), and the equality P(x, 0) = 0 must hold. It is clear that the
existence of this narrow region around the point I ∼ 0 does not affect the behavior of
moments (13.81) for larger β
0
(x).
Asymptotic formulas (13.81) and (13.82) describe the transition to the region of
saturated intensity fluctuations, where β(x) → 1 for β
0
(x) → ∞. In this region, we
have correspondingly
I
n
(x, R)
= n!, P(x, I) = e
−I
. (13.83)
The exponential probability distribution (13.83) means that complex field u(x, R)
is the Gaussian random field. Recall that
u(x, R) = A(x, R)e
iS(x,R)
= u
1
(x, R) + iu
2
(x, R), (13.84)
where u
1
(x, R) and u
2
(x, R) are the real and imaginary parts, respectively. As a result,
the wavefield intensity is
I(x, R) = A
2
(x, R) = u
2
1
(x, R) + u
2
2
(x, R).
From the Gaussian property of complex field u(x, R) follows that random fields
u
1
(x, R) and u
2
(x, R) are also the Gaussian statistically independent fields with
variances
D
u
2
1
(x, R)
E
=
D
u
2
2
(x, R)
E
=
1
2
. (13.85)
It is quite natural to assume that their gradients
p
1
(x, R) = ∇
R
u
1
(x, R) and p
2
(x, R) = ∇
R
u
2
(x, R)

380 Lectures on Dynamics of Stochastic Systems
are also statistically independent of fields u
1
(x, R) and u
2
(x, R) and are the Gaussian
homogeneous and isotropic (in plane R) fields with variances
σ
2
p
(x) =
D
p
2
1
(x, R)
E
=
D
p
2
2
(x, R)
E
. (13.86)
With these assumptions, the joint probability density of fields u
1
(x, R), u
2
(x, R)
and gradients p
1
(x, R) and p
2
(x, R) has the form
P(x;u
1
, u
2
, p
1
, p
2
) =
1
π
3
σ
4
p
(x)
exp
(
−u
2
1
− u
2
2
−
p
2
1
+ p
2
2
σ
2
p
(x)
)
. (13.87)
Consider now the joint probability density of wavefield intensity I(x, R) and ampli-
tude gradient
κ(x, R) = ∇
R
A(x, R) =
u
1
(x, R)p
1
(x, R) + u
2
(x, R)p
2
(x, R)
q
u
2
1
(x, R) + u
2
2
(x, R)
.
We have for this probability density the expression
P(x;I, κ) =
h
δ
(
I(x, R) − I
)
δ
(
κ(x, R) − κ
)
i
u
i
,p
i
=
1
π
3
σ
4
p
(x)
∞
Z
−∞
du
1
∞
Z
−∞
du
2
Z
dp
1
Z
dp
2
exp
(
−u
2
1
− u
2
2
−
p
2
1
+ p
2
2
σ
2
p
(x)
)
× δ
u
2
1
+ u
2
2
− I
δ
u
1
p
1
+ u
2
p
2
q
u
2
1
+ u
2
2
− κ
=
1
2πσ
2
p
(x)
exp
(
−I −
κ
2
2σ
2
p
(x)
)
. (13.88)
Consequently, the transverse gradient of amplitude is statistically independent of
wavefield intensity and is the Gaussian random field with the variance
D
κ
2
(x, R)
E
= 2σ
2
p
(x). (13.89)
We note that the transverse gradient of amplitude is also independent of the second
derivatives of wavefield intensity with respect to transverse coordinates.
At the end of this section, we note that the path integral representation of field
u(x, R) makes it possible to investigate the applicability range of the approximation
of delta-correlated random field ε(x, R) in the context of wave intensity fluctuations.
It turns out that all conditions restricting applicability of the approximation of delta-
correlated random field ε(x, R) for calculating quantity
h
I
n
(x, R)
i
coincide with those

Caustic Structure of Wavefield in Random Media 381
obtained for quantity
I
2
(x, R)
. In other words, the approximation of delta-correlated
random field ε(x, R) does not affect the shape of the probability distribution of wave-
field intensity.
In the case of turbulent temperature pulsations, the approximation of the delta-
correlated random field ε(x, R) holds in the region of weak fluctuations under the
conditions
λ
√
λx x,
where λ = 2π/k is the wavelength.
As to the region of strong fluctuations, the applicability range of the approximation
of delta-correlated random field ε(x, R) is restricted by the conditions
λ ρ
coh
r
0
x,
where ρ
coh
and r
0
are given by Eqs. (13.21), page 360, and (13.67), page 374. The
physical meaning of all these inequalities is simple. The delta-correlated approxima-
tion remains valid as long as the correlation radius of field ε(x, R) (its value is given
by the size of the first Fresnel zone in the case of turbulent temperature pulsations) is
the smallest longitudinal scale of the problem. As the wave approaches at the region
of strong intensity fluctuations, a new longitudinal scale appears; its value ∼ ρ
coh
√
kx
gradually decreases and can become smaller than the correlation radius of field ε(x, R)
for sufficiently large values of parameter β
0
(x). In this situation, the delta-correlated
approximation fails.
We can consider the above inequalities as restrictions from above and from below
on the scale of the intensity correlation function. In these terms, the delta-correlated
approximation holds only if all scales appearing in the problem are small in compari-
son with the length of the wave path.
13.4 Elements of Statistical Topography of Random
Intensity Field
The above statistical characteristics of wavefield u(x, R), for example, the intensity
correlation function in the region of strong fluctuations, have nothing in common
with the actual behavior of the wavefield propagating in particular realizations of the
medium (see Figs. 13.1 and 13.2). In the general case, wave field intensity satisfies
Eq. (13.26), page 362,
∂
∂x
I(x, R) +
1
k
∇
R
[
I(x, R)∇
R
S(x, R)
]
= 0,
I(0, R) = I
0
(R),
(13.90)
from which follows that the power of wave field in plane x =const remains intact for
arbitrary incident wave beam:
E
0
=
Z
I(x, R)dR =
Z
I
0
(R)dR.

382 Lectures on Dynamics of Stochastic Systems
(a) (b)
Figure 13.1 Transverse section of laser beam propagating in turbulent medium in the regions
of (a) strong focusing and (b) strong (saturated) fluctuations. Experiment in laboratory condi-
tions.
(a) (b)
Figure 13.2 Transverse section of laser beam propagating in turbulent medium in the regions
of (a) strong focusing and (b) strong (saturated) fluctuations. Numerical simulations.
Eqs. (13.90) can be treated as the equation of conservative tracer transfer in the
potential velocity field in the conditions of tracer clustering. As a consequence, real-
izations of the wave intensity field also must show cluster behavior. In the case under
consideration, this phenomenon appears in the form of caustic structures produced
due to random processes of wave field focusing and defocusing in random medium.
For example, Fig. 13.1 shows photos of the transverse sections of laser beam prop-
agating in turbulent medium [80] for different magnitudes of dielectric permittivity
fluctuations (laboratory investigations). Figure 13.2 shows similar photos borrowed
from [81]. These photos were simulated numerically [82, 83]. Both figures clearly
show the appearance of caustic structures in the wave field.
In order to analyze the detailed structure of wavefield, one can use methods of sta-
tistical topography [69]; they provide an insight into the formation of the wavefield
caustic structure and make it possible to ascertain the statistical parameters that des-
cribe this structure.
If we deal with the plane incident wave, all one-point statistical characteristics,
including probability densities, are independent of variable R in view of spatial homo-
geneity. In this case, a number of physical quantities that characterize cluster structure
of wavefield intensity can be adequately described in terms of specific (per unit area)
values.

Caustic Structure of Wavefield in Random Media 383
Among these quantities are:
l
specific average total area of regions in plane {R}, which are bounded by level lines of
intensity I(x, R) inside which I(x, R) > I,
h
s(x, I)
i
=
∞
Z
I
dI
0
P(x;I
0
),
where P(x;I) is the probability density of wavefield intensity;
l
specific average field power within these regions
h
e(x, I)
i
=
∞
Z
I
I
0
dI
0
P(x;I
0
);
l
specific average length of these contours per first Fresnel zone L
f
(x) =
√
x/k
h
l(x, I)
i
= L
f
(x)
h
|p(x, R)|δ
(
I(x, R) − I
)
i
,
where p(x, R) = ∇
R
I(x, R) is the transverse gradient of wavefield intensity;
l
estimate of average difference between the numbers of contours with opposite normal ori-
entation per first Fresnel zone
h
n(x, I)
i
=
1
2π
L
2
f
(x)
h
κ(x, R;I)|p(x, R)|δ
(
I(x, R) − I
)
i
,
where κ(x, R;I) is the curvature of the level line,
κ(x, R;I) =
−p
2
y
(x, R)
∂
2
I(x, R)
∂z
2
− p
2
z
(x, R)
∂
2
I(x, R)
∂y
2
p
3
(x, R)
+ 2
p
y
(x, R)p
z
(x, R)
∂
2
I(x,R)
∂y∂z
p
3
(x, R)
.
The first Fresnel zone plays the role of the natural medium-independent length scale
in plane x = const. It determines the size of the transient light–shadow zone appeared
in the problem on diffraction by the edge of an opaque screen.
Consider now the behavior of these quantities with distance x (parameter β
0
(x)).
13.4.1 Weak Intensity Fluctuations
The region of weak intensity fluctuations is limited by inequality β
0
(x) ≤1. In this
region, wavefield intensity is the lognormal process described by probability distribu-
tion (13.37).
The typical realization curve of this logarithmic-normal process is the exponen-
tially decaying curve
I
∗
(x) = e
−
1
2
β
0
(x)
,
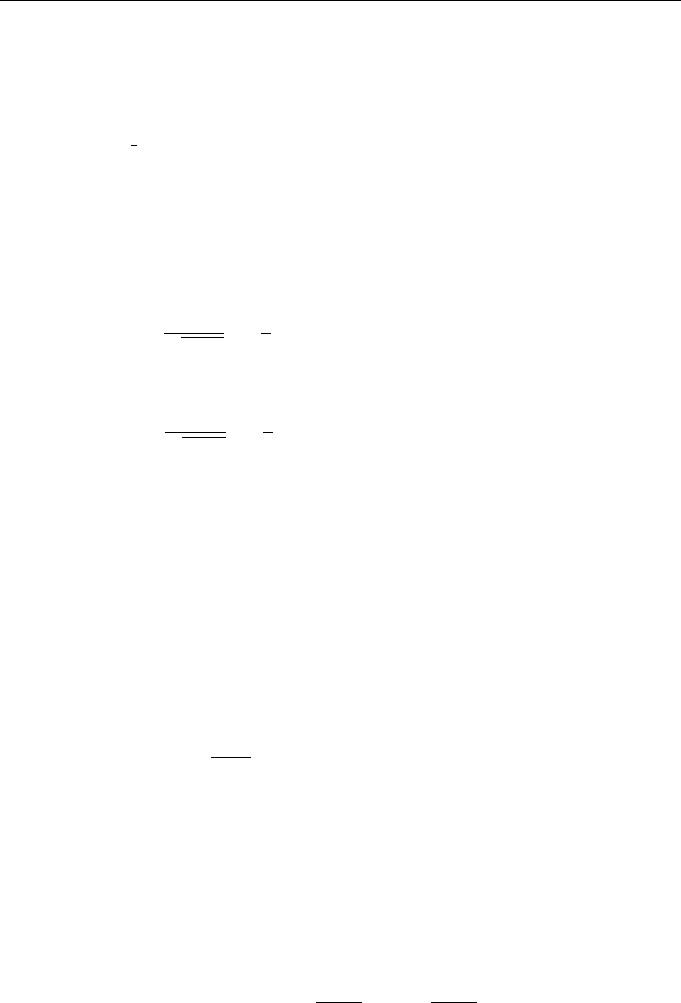
384 Lectures on Dynamics of Stochastic Systems
and statistical characteristics (moment functions
h
I
n
(x, R)
i
, for example) are formed
by large spikes of process I(x, R) relative this curve.
In addition, various majorant estimates are available for lognormal process realiza-
tions. For example, separate realizations of wavefield intensity satisfy the inequality
I(x) < 4e
−
1
4
β
0
(x)
for all distances x ∈ (0, ∞) with probability p = 1/2. All these facts are indicative of
the onset of cluster structure formations in wavefield intensity.
As we have seen earlier, the knowledge of probability density (13.37) is sufficient
for obtaining certain quantitative characteristics of these cluster formations. For exam-
ple, the average area of regions within which I(x, R) > I is
h
s(x, I)
i
= Pr
1
√
β
0
(x)
ln
1
I
e
−β
0
(x)/2
, (13.91)
and specific average power confined in these regions is given by the expression
h
e(x, I)
i
= Pr
1
√
β
0
(x)
ln
1
I
e
β
0
(x)/2
, (13.92)
where probability integral function Pr(z) is defined as (4.20), page 94.
The character of cluster structure spatial evolution versus parameter β
0
(x) essen-
tially depends on the desired level I. In the most interesting case of I > 1, the val-
ues of these functions in the initial plane are
h
s(0, I)
i
=0 and
h
e(0, I)
i
=0. As β
0
(x)
increases, small cluster regions appear in which I(x, R) > I; for certain distances, these
regions remain almost intact and actively absorb a considerable portion of total energy.
With further increasing β
0
(x), the areas of these regions decrease and the power within
them increases, which corresponds to an increase of regions’s average brightness. The
cause of these processes lies in radiation focusing by separate portions of medium.
Figure 13.3 shows functions
h
s(x, I)
i
and
h
e(x, I)
i
for different parameters β
0
(x)
from a given range. The specific average area is maximum at β
0
(x) = 2 ln(I), and
h
s(x, I
i
max
= Pr
−
√
2 ln I
.
The average power at this value of β
0
(x) is
h
e(x, I)
i
= 1/2.
In the region of weak intensity fluctuations, the spatial gradient of amplitude level
∇
R
χ(x, R) is statistically independent of χ (x, R). This fact makes it possible both to
calculate specific average length of contours I(x, R) = I and to estimate specific ave-
rage number of these contours. Indeed, in the region of weak fluctuations, probability
density of amplitude level gradient q(x, R) = ∇
R
χ(x, R) is the Gaussian density
P(x;q) =
h
δ
(
∇
R
χ(x, R) − q
)
i
=
1
σ
2
q
(x)
exp
(
−
q
2
σ
2
q
(x)
)
, (13.93)
where σ
2
q
(x) =
q
2
(x, R)
is the variance of amplitude level gradient given by
Eq. (13.44), page 366.
Caustic Structure of Wavefield in Random Media 385
0.4 0.8 1.2
β
0
I = 1.5
I = 2.5
0.05
0.1
0.15
〈s (x, l )〉
0.4 0.8 1.2
I = 1.5
I = 2.5
0.2
0.4
0.6
〈e (x, l )〉
(a)
β
0
(b)
Figure 13.3 (a) Average specific area and (b) average power versus parameter β
0
(x).
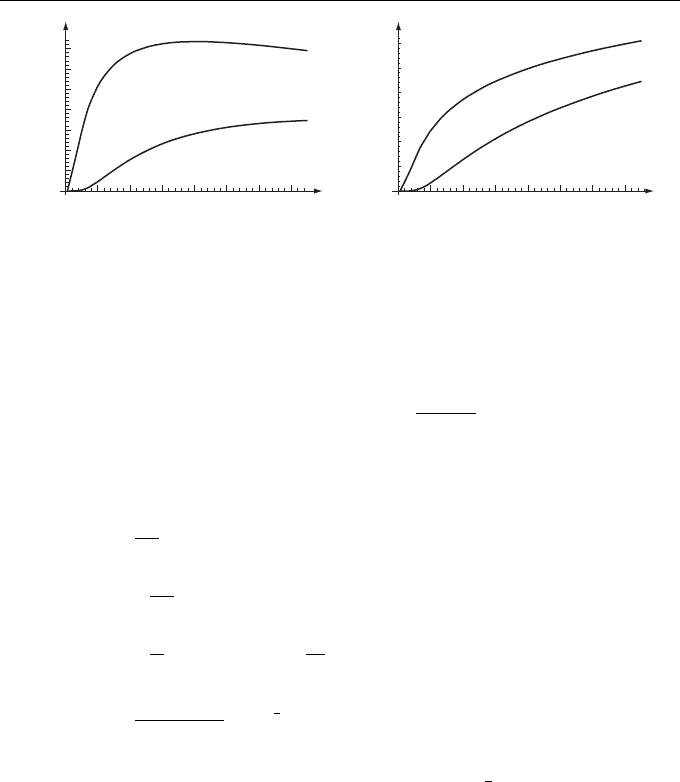
As a consequence, we obtain that the specific average length of contours is descri-
bed by the expression
h
l(x, I)
i
= 2L
f
(x)
h
|q(x, R)|
i
IP(x;I) = L
f
(x)
q
πσ
2
q
(x)IP(x;I). (13.94)
For the specific average number of contours, we have similarly
h
n(x, I)
i
=
1
2π
L
2
f
(x)
h
κ(x, R, I)|p(x, R)δ
(
I(x, R) − I
)
i
= −
1
2π
L
2
f
(x)I
h
1
R
χ(x, R)δ
(
I(x, R) − I
)
i
= −
1
π
L
2
f
(x)
D
q
2
(x, R)
E
I
∂
∂I
IP(x;I)
=
L
2
f
(x)σ
2
q
(x)
πβ
0
(x)
ln
Ie
1
2
β
0
(x)
IP(x;I). (13.95)
We notice that Eq. (13.95) vanishes at I = I
0
(x) = exp{−
1
2
β
0
(x)}. This means that
this intensity level corresponds to the situation in which the specific average number
of contours bounding region I(x, R) > I
0
coincides with the specific average number
of contours bounding region I(x, R) < I
0
. Figures 13.4 show functions
h
l(x, I)
i
and
h
n(x, I)
i
versus parameter β
0
(x).
Dependence of specific average length of level lines and specific average number of
contours on turbulence microscale reveals the existence of small-scale ripples imposed
upon large-scale random relief. These ripples do not affect the redistribution of areas
and power, but increases the irregularity of level lines and causes the appearance of
small contours.
As we mentioned earlier, this description holds for β
0
(x) ≤1. With increasing para-
meter β
0
(x) to this point, Rytov’s smooth perturbation method fails, and we must
consider the nonlinear equation in wavefield complex phase. This region of fluctua-
tions called the strong focusing region is very difficult for analytical treatment. With
