Клейн Л.С. Время кентавров. Степная прародина греков и ариев

Подождите немного. Документ загружается.

IX. Игры с богами

317

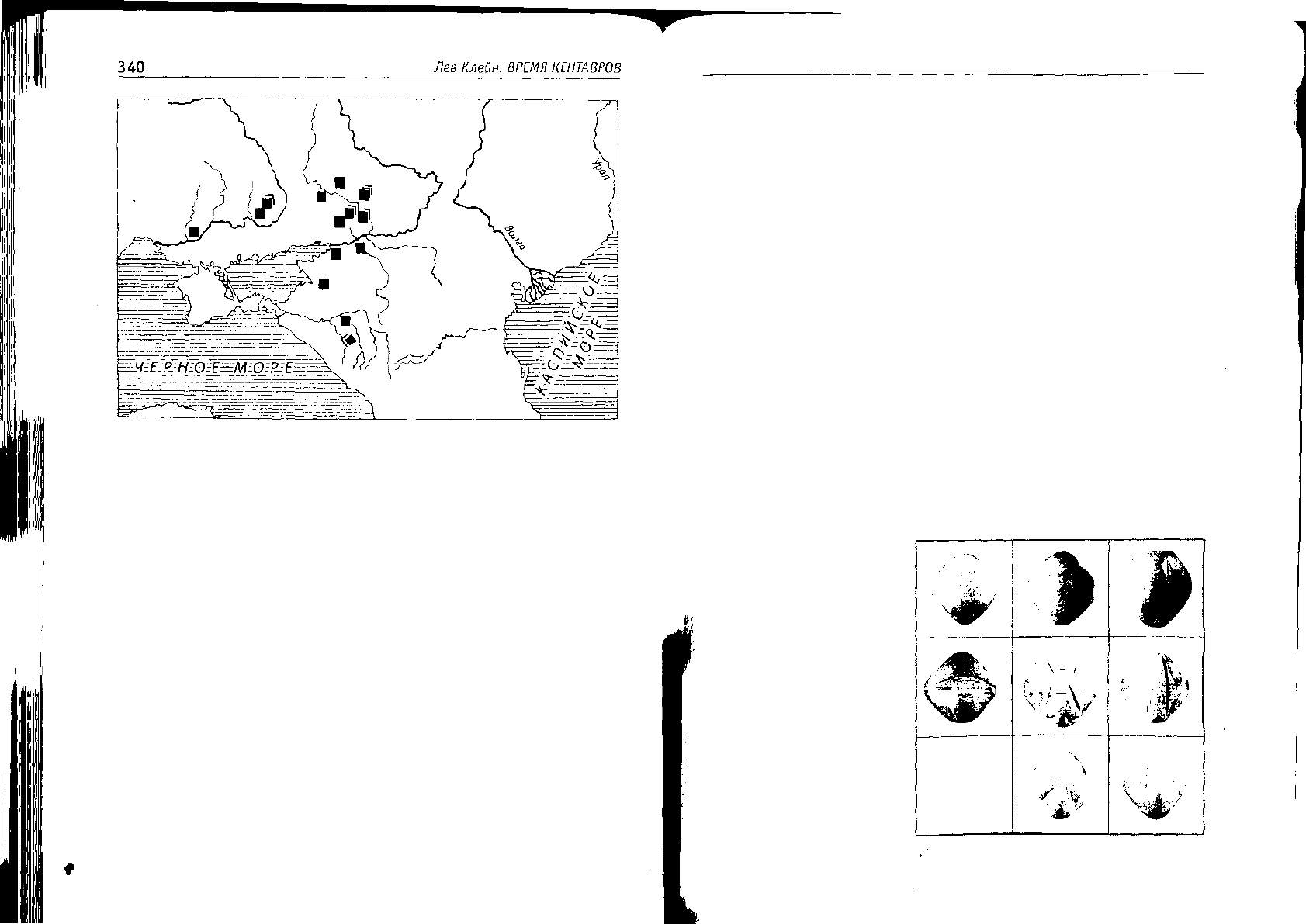
Рис. 115. Наборы игральных костей бронзового века в Северном Причерноморье

и Предкавказье, карта (Клейн, 1987; Klejn, 1999)

Во-первых, четыре крупных числа натурального ряда все-таки не могут выпасть

в виде сумм вообще — это 11,14,16 и 17. Никакая комбинация трех костей не

даст в сумме ни одного из этих чисел. Во-вторых, шансы выпадения остальных

сумм неравны, и игроки могли это заметить на опыте: скажем, 7 и 9 выпадают

в 9 раз чаще, чем 0 или 18 (у них возможностей образования в 9 раз больше).

Конечно, вычислить подлинные различия в вероятности выпадения люди того

времени были не в состоянии. Чтобы оценить значение перестановок для таких

вычислений, потребовались уровень мышления XVII в. н. э. и гений Паскаля,

а у новосвободненских игроков не было даже нумерации (индивидуализации)

костей. Но подметить неравенство в распределении комбинаций по суммам они

были в состоянии. Они видели, что пять суммарных чисел (3, 6, 7, 9 и 12) име-

ют по две возможности образования, т. е. по два состава реальных слагаемых,

тогда как остальные 9 чисел (с нулем 10) могут быть образованы только одним

способом каждое. Такая раскладка создавала у смышленых игроков впечатле-

ние неравенства шансов в получении тех или иных сумм очков.

Это должно было толкать их на поиски путей усовершенствования игры.

Следующую стадию развития игры находим в катакомбных культурах

(рис. 115). Кости здесь не столь продолговатые, как в Кладах, не столь

тщательно обработанные, но тоже четырехгранные. Есть большие наборы

(трехкостные) и малые (двухкостные).

Больших (т. е. трехкостных) катакомбных наборов костей открыто во-

семь. Все эти наборы во многом повторяют, с некоторым огрублением, ново-

свободненское оформление игры. Учитывая датировку катакомбной культур-

ной общности (со второй половины III тыс. до н. э.) и новосвободненские

вклады в катакомбном культурном материале (бронзовые тесла и втульчатые

крюки, выпуклые стенки и галечную подстилку могил), позволительно рас-

сматривать катакомбную игру в кости как продолжение новосвободненской

традиции (возможно, через посредников).

Однако в технике игры налицо отнюдь не огрубление. Наоборот, в боль-

ших катакомбных наборах представлено дальнейшее усовершенствование

игры: ноль здесь заменяет не четверку, а тройку, четверка же оставлена в ряду

обозначений сторон. Это совершенно ясно видно на наборах из Предкавказья

и Донеччины. Обозначения иные, чем на костях из Кладов, но соответствия

устанавливаются без труда. Я пока не могу объяснить, почему этих обозначе-

ний две системы (причем это двоение продолжается и в малых наборах.

Первая система обозначений — в основном точками на плоскостях. В таких

наборах пустая сторона, конечно, означает ноль, единица и четверка недвус-

мысленно обозначены точками (как на передне- и южноазиатских кубиках).

Оставшаяся продольная черта означает число выдающееся, коль скоро для него

избран особый, незаурядный, выделяющийся знак. Поскольку минимальные

значения в ряду чисел (0 и 1) уже заняты, остается максимальное. Это могут

быть пятерка или шестерка. 14 6

Схожесть с новосвободнен-

скими рядами побуждает

видеть в этом максимальном д

числе шестерку. Итак, здесь

ряд 0,1,4,6.

Вторая система —

фигурные нарезные знаки

на гранях (рис. 116). Знаки g

фигурные, сделаны нарез-

ками. Они расположены не

на плоскостях, а на скру-

гленных ребрах, глядящих

кверху при стабилизации в

кости на месте выпадения.

Пустое место соответствует

нулю, единица обозначается

Рис

тройной линией, но концы

116. Системы цифровых обозначений на катакомбных

игральных костях (Клейн, 1987 — Klejn, 1999)

326

326 Лев Клейн. ВРЕМЯ КЕНТАВРОВ

трех линий вверху и внизу собраны в пучки: нет трех свободных линий — ими

очерчена одна фигура, похожая на прорисовку щели. Несомненно, шестерку

изображают два клиновидных треугольника основаниями друг к другу (как бы

составной ромб). Примечательно, что и здесь, как в Кладах (новосвободнен-

ской культуры), шестерка явно показана составной — из двух троек.

Оставшийся знак — крестовидный квадрат, квадрат с вогнутыми сторона-

ми (как в карточном обозначении бубен), с выступающими из углов рисками,

продолжающими диагонали, — не может означать ничего иного, кроме четвер-

ки. Крестом обозначается четверка в индийской письменности кхарошти и в ки-

тайском коммерческом письме, квадратом — в старых китайских иероглифах.

Итак, в фигурных знаках представлен тот же ряд, что и на костях с точ-

ками: 0,1,4, б.

Замена тройки четверкой произошла еще на новосвободненском этапе:

на костях еще тройка, а на дополнительных серебряных палочках — уже чет-

верка. В катакомбных — только четверка. Почему в этих наборах четверка за-

местила тройку, трудно сказать. Возможно, что культуре, в которой произошел

этот переход (будь то новосвободненская, или северокавказская, или одна из

катакомбных), было свойственно особое пристрастие к чету, к четверичности,

к четвертному делению, к квадратным структурам.

Еще А. Гётце подметил, что в центрально-европейском неолите противо-

стояли друг другу два культурных мира с различными структурно-числовыми

(делительными) предпочтениями, выражавшимися в архитектонике глиняной

посуды.

В мире линейно-ленточной керамики мастер всегда предпочитал рас-

полагать ручки в трех местах сосуда на равном расстоянии друг от друга, т. е.

делить сосуд в плане натрое, как бы вписывая в круг равносторонний тре-

угольник. Сейчас установлено палеогенетическим анализом, что население

Южной Европы и Подунавья, в частности люди линейно-ленточной керамики,

прибыли с Ближнего Востока и притащили с собой в Европу земледелие и ско-

товодство — неолит. Трехчастное деление — это их предпочтение (мы видели

его отзвуки на Кавказе).

Севернее же Дуная, в мире шнуровой керамики, воронковидных кубков

и шаровидных амфор, сосуд, как я уже сообщал, делили в плане на четыре ча-

сти, ручки располагали крестообразно, и если даже требовалось разместить

только три ручки, их все равно располагали в тех же местах — по концам во-

ображаемого креста, а четвертый конец креста оставляли свободным. Это

население генетически восходит к местным охотничье-собирательским пле-

менам, которые заимствовали у пришельцев новые способы хозяйствования.

Непременные четыре стороны — это их представление о мире.

IX. Игры с богами 172

342

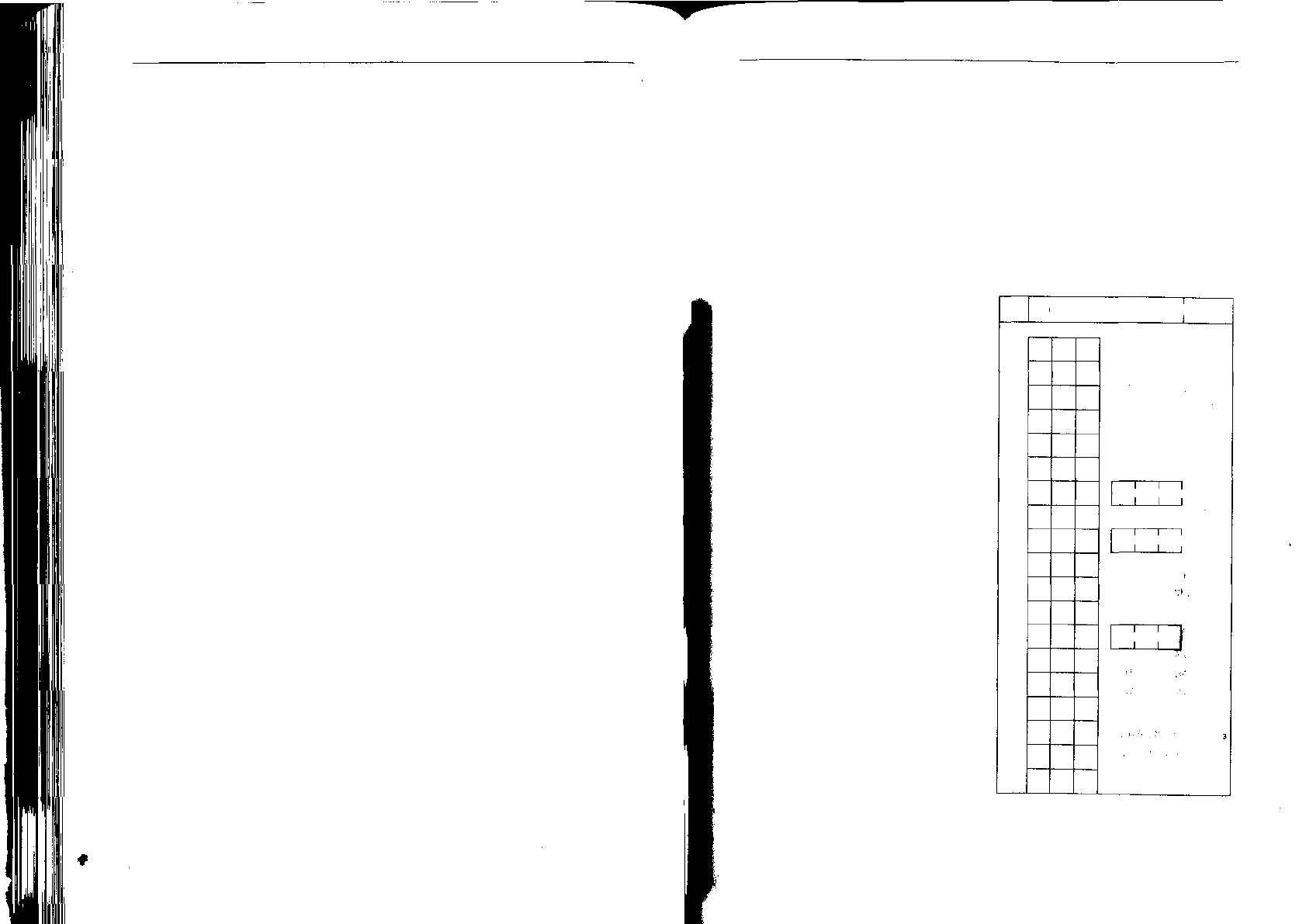
Полная матрица возможных сочетаний и сумм чисел

очков при совместном метании трех

новосвободненских костей (со знаками сторон 0,1,4, 6}

В основе новосвободненской культуры есть вклады воронковидных куб-

ков и шаровидных амфор. Боевые топоры северокавказской явно происходят

от многогранных топоров «с набалдашником» и изломом оси, характерных

для культуры воронковидных кубков. Донецкая катакомбная культура мо-

жет в некотором аспекте быть рассмотрена как культура шнуровой керамики.

А в предкавказской катакомбной культуре четверичная структура наглядно

и обильно представлена основаниями курильниц.

Возможно и иное, рационально-прагматическое объяснение причины по-

явления четверки на катакомбных

игральных костях. И если даже оно

не правдоподобнее первого, итог все

же имел рационально-прагматический

смысл: система стала совершеннее.

Ведь при наличии трех костей с еди-

ницами нет надобности в тройке. Бли-

жайшее следующее число, которое

желательно выразить одним знаком, —

именно четверка. Система оказывается

логичнее, полнее и строже, чем ново-

свободненская (рис. 117). Здесь всего

два места в натуральном ряду сумм не

заполнено (там было 4) и всего три сум-

мы имеют по два способа образования,

по две комбинации (там таких сумм

было б), а максимальное превышение

вероятности выпадения любой из са-

мых счастливых сумм над любой из са-

мых несчастливых здесь шестикратное

(там было девятикратное).

Двухкостных наборов в ката-

комбных погребениях шесть: три с фи-

гурными знаками, один — с точечными

и еще два набора — с сочетанием тех

и других. Есть и погребения с одной

игральной костью. По-видимому,

двухкостные наборы и наличие одной

КОСТИ В погребении надо рассматри- Всего сочетаний 20, с перестановками —64.

вать как неполные наборы, а ИХ ПО- Рис. И7. Игра в кости с большим катакомбным

явление — как некоторую «порчу», набором (Клейн, 1987; Klejn, 1999)

Суммы

^лагае

мые [о чки на костях) Шансы

выпадения

0 0 1

2 1 1

1 1

4 0

6 0 0 3+3'=6

6 1

'' ' 6

8 6 1

4 4 0 3+3=6

4 4

б 4

;••'< 6

0 4 4 4(

;" 3+1=4

6 6

б 4

344

Лев Клейн. ВРЕМЯ КЕНТАВРОВ

Суммы

Слагаемые (очки на костях)

Шансы

выпадения

+ 1=3

0 0

+ 1=3

2 1

+ 1=3

3 1

2 2

+ 1=3

3 3

+ 1=3

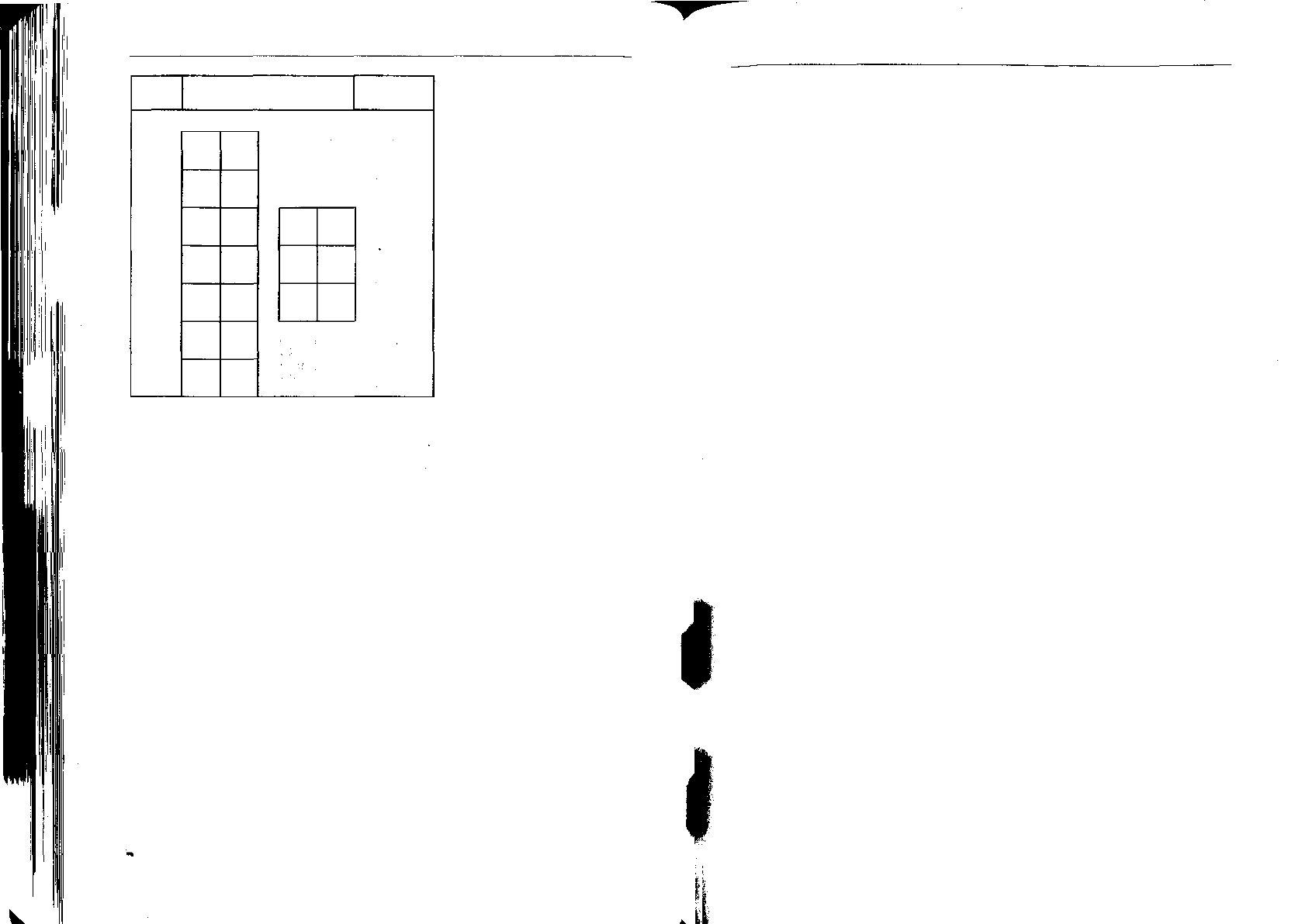
Всего сочетаний 10, с перестановками — 16.

Рис. 118. Игра с малым катакомбным набором

(Клейн, 1987; Klejn, 1999)

нарушение строгости тради-

ции (рис. 118).

Трудно сказать, было ли

оно глубоким или внешним,

то есть уже играли с непол-

ными наборами или только

клали неполный набор в мо-

гилу (по каким-то частным

причинам). По крайней мере

в Шпаковке представлен

двухкостный набор, кото-

рым, видимо, играли. До-

полнительная палочка несет

на себе шесть нарезок, то

есть число, обозначающее

максимальный выброс при

броске одной кости, при ну-

левом значении на двух дру-

гих палочках. Возможно, это

должно компенсировать от-

сутствие третьей кости. Вообще же наличие этих трех палочек подчеркивает

преемственность от новосвободненской игры — там ведь тоже есть не только

две серебряные палочки с нарезкой, но и три гладких деревянных палочки.

Но вот некоторые из этих наборов отличаются от остальных географи-

ческим положением и знаками. Они дальше, чем все остальные, от новосво-

бодненского очага по территории и, вероятно, во времени, т. е. они позже

остальных. Не стану подробно описывать их,укажу только, что на них, по моей

реконструкции, получается натуральный ряд чисел: 0,1, 2, 3. Анализ сумм оч-

ков, которые две кости с такой разметкой могут дать при совместном выбросе,

привел меня к следующим выводам. Здесь игра несколько упрощена и заметно

улучшена. Совершенно исчезли пустые места в натуральном ряду суммарных

чисел. Срединные суммы уравнены между собой по количеству способов их

образования. Крайние — тоже уравнены между собой. А вероятности выпа-

дения сумм образовали нормальное распределение с пиком в середине табли-

цы и с небольшим размахом различий между вероятностями (максимальная

всего в 4 раза больше минимальной).

Та же система обнаружена в памятниках примерно той же эпохи на пути

в Индию (в Средней Азии) и в самой Индии. При раскопках Алтын-тепе в одном

А13 кладов в стенах дома, в комплексе конца III — начала II тыс. до н. э.,

IX. Игры с богами

345

обнаружены четырехгранные палочки из слоновой кости с кружками на трех

сторонах. Кружков, соответственно, 1, 2 и 3. Четвертая сторона, без кружков,

видимо, обозначает «пусто», хоть она и не совсем пуста: с орнаментом. Пало-

чек этих здесь, однако, 3. Аналогичные палочки с кружками, с той же размет-

кой (0, 1, 2, 3), как отмечает В. М. Массон, найдены в Индии в верхних слоях

Мохенджо-Даро.

7. Какой игра пришла в Индию. Чтобы добиться дальнейшего совер-

шенствования игры, представляется возможным только один путь: перестать

подсчитывать очки, а сравнивать сами комбинации костей. Например: едини-

ца + единица + четыре — это одна комбинация, а пусто + пусто + шестер-

ка — другая (хотя сумма очков одна). То есть от операций с суммами очков (по

двум или трем костям) перейти к операциям с самими сочетаниями выпадов

этих костей (без суммирования очков). Тогда не будет уравнивания разных

сочетаний, у которых одинаковые суммы. Ведь все такие сочетания (комбина-

ции) выглядят равновозможными, а что на самом деле это не так, можно было

догадаться, только оценив значение перестановок. Тогда выяснилось бы, что

комбинации из одинаковых цифр выпадают редко, со включением иной циф-

ры — чаще, а из разных цифр — особенно часто. Но это было делом далекого

будущего. Да и как было заметить самый эффект перестановок, когда кости не

имели индивидуальных помет и однозначные цифры разных костей шли как

равноправные? Оставалось уповать на равновозможность комбинаций.

Комбинаций этих при трех костях всегда 20 (или, если не считать комби-

нации из одних нулей, 19), а при двух костях — 11 (или, без нулей, 10).

Но при таком изменении подхода отпадают многие ограничения и напра-

шиваются изменения ряда особенностей игры.

Во-первых, тогда не нужен нуль (незачем регулировать соотношения

между единицей и суммой очков двух или трех выпадов); он даже оказыва-

ется помехой, так как психологически затрудняет восприятие комбинаций как

значимых и — особенно — как равноправных.

Во-вторых, не требуются определенные интервалы между значениями сто-

рон, ибо не нужно регулировать подсчет очков. Интервалы могут сохраняться

по традиции, могут произвольно изменяться ради обновления и разнообразия,

а могут быть ликвидированы в угоду тяге к упрочению (череду значений сторон

можно сделать натуральным рядом чисел). В санскритских текстах Пашакаке-

вали, восходящих к IV в. до н. э., описываются употребляемые для гадания три

палочки с кружками, представляющими натуральный ряд без нуля: 1, 2,3,4.

В-третьих, необязательными вообще становятся числовые значения

для знаков на сторонах кости (хотя такие значения и остаются возможными

326

Лев Клейн. ВРЕМЯ КЕНТАВРОВ

и даже удобными). Но зато, наоборот, обязательными (и уж это безусловно)

становятся особые, словесные, нечисловые названия для комбинаций. Опре-

деления через суммы очков не годятся, так как нередко совпадают у равных

комбинаций, а составными числами (например, l-4-б или 1-6-4) трудно опери-

ровать в игре: легко сбиться.

В-четвертых, требуется иной критерий определения выигрыша или

проигрыша. Подсчет очков и количественное сравнение результатов теря-

ют смысл, а на их место становится соревнование в скорейшем достижении

некоторых комбинаций, заданных правилами игры или заранее произвольно

загаданных игроками. В первом случае только заданные комбинации нужда-

ются в названии, во втором случае собственные названия должны быть у всех

возможных комбинаций.

Именно эту систему мы и застаем в позднейшей Индии, куда ведут к ари-

ям многообразные линии преемственности от катакомбной культурной общ-

ности. Там, в Индии, эта система подробно зафиксирована средневековыми

письменными источниками, и она явно пришла туда с ариями. Об этом говорит

четырехсторонность костей — это ведь очень редкая особенность. Таким об-

разом, нуль был изобретен еще в Причерноморье, а в Индию эта система игры

пришла уже без необходимости нуля.

8. Чатурашра. В Индии совершенно четко обособлены две чуждых

одна другой системы игры. Одна — в хараппской (доарийской) цивилизации,

другая —у ариев.

До прихода ариев население Северо-Западного Индостана знало и лю-

било игру в кости. В поселениях хараппской цивилизации (сер. III тыс. —

XVIII в. до н. э.) обильно представлены игральные кости, но какие? Это ку-

бики — керамические, каменные и изредка фаянсовые. В Мохенджо-даро, по

сообщению Дж. Маршалла, много игральных костей, из них он опубликовал

4, а его продолжатель Э. Маккей отметил, что находил кости на всех уровнях;

опубликовал он 6 костей. Из хараппских горизонтов Хараппы опубликовано

7 экземпляров, из Аламгирпура 1 и из Лотхала 1. Таким образом, всего опубли-

ковано 19 кубиков, а найдено, видимо, гораздо больше.

Разметка сторон у кубиков здесь такая же, как в Передней Азии, т. е. не

совпадающая с индоевропейской «правильной» (не дающая сумму 7 при сложе-

нии противоположно размещенных чисел). Обычная разметка: 1-2, 3-4, 5-6 или

1-2, 3-5,4-6, реже 1-3, 2-4, 5-6, или 1-2, 3-6,4-5, или 1-3, 2-5,4-0. И только один

кубик из Хараппы имеет «правильную» разметку: 1-6, 2-5,3-4 (рис. 112).

В арийской же Индии — так же, как в катакомбной общности, — было

'две основных разновидности игры в кости: одна — с произвольным, нередко

IX. Игры с богами

347

большим количеством неразмеченных костей (как в катакомбных альчиках),

другая — со стандартным набором костей, имеющих размеченные стороны.

Меня здесь интересует эта вторая. Ее кости назывались «пашака» (pasaka,

pasa, иногда prasaka, возможно, от корня pras— «брос-ать»),

И в современном обиходе (по этнографическим наблюдениям), и в сред-

невековье (судя по рукописям оракулов), и в древности (судя по Махабхарате

IV, 50, 24) игральные кости этой игры в Индии оказываются — так же, как рас-

смотренные кости бронзового века Причерноморья, — четырехсторонними,

чатурашра fcaturasra, faturamsa), закругленными на узких концах.

И — так же, как в больших катакомбных наборах, — в практике оракулов

полагалось метать три кости сразу, а если есть только одна кость, то метать ее

трижды кряду.

На костях современных народных игр обозначения сторон делались по-

разному в разных местностях: то это 1, 3, 4, 6, то 1, 2, 5, 6, а в оракулах кости

всегда размечаются натуральным рядом чисел — 1, 2, 3, 4; в Тибете вместо

цифр — буквы: а, уа, va, da.

Как показал Г. Людерс, индийская игра с размеченными костями заключа-

лась в том, что каждый из игроков загадывал заранее одну из возможных комби-

наций; кому удастся первым выметать свою, тот и выиграл. Людерс показал так-

же, что в оракулах использовались те же комбинации, далее, что общий термин

для такой комбинации был ayas и что каждая имела свое собственное название.

Если все комбинации являются значащими (т. е. если нулевые сочетания

вообще отсутствуют или при наличии не изымаются), то, какими бы цифрами

ни размечались четыре стороны костей, при выпадении трех костей образу-

ется ровно 20 комби-

наций выпадения. При

разметке цифрами 1,

2, 3, 4 это следующие

комбинации (рис. 119).

Если же учиты-

вать и перестановки

внутри каждой комби-

нации, т. е. последова-

тельность чисел в ней

(например, 1-2-3, или

1-3-2, или 3-2-1 и т.п.),

то выбор для загады-

вания расширяется

до 64 позиций: есть 4

Группы

две

Всего

Комбинации

(сочетания)

и их

слагаемые

{очки

на костях)

Комбинации

(сочетания)

и их

слагаемые

{очки

на костях)

111

112

113

114 123

Комбинации

(сочетания)

и их

слагаемые

{очки

на костях)

222

221 223

224

124

Комбинации

(сочетания)

и их

слагаемые

{очки

на костях)

333

331 332

334 134

Комбинации

(сочетания)

и их

слагаемые

{очки

на костях)

444 441 442 443

234

Комбинации

(сочетания)

и их

слагаемые

{очки

на костях)

Итого сочетаний

4 12 4

Шансы выпа-

дения каждого

1 3 6

С перестанов-

ками

4x1=4 12x3=36 4x6=24

Рис. 119. Индийская игра в кости («пашака»)

(Клейн, 1987; Klejn, 1999)

326

Лев Клейн. ВРЕМЯ КЕНТАВРОВ

сочетания (из одинаковых цифр), не имеющих перестановок, 12 имеющих по 3

перестановки, и 4 (у которых все цифры разные) — по б (рис. 119).

Видимо, эта возможность использовалась в оракулах, и это был шаг (для

своего времени необычайно прозорливо продуманный) к лучшей технике по-

лучения случайных цифр, в которой, наконец, полностью уравнивались шансы

выпадения. Три кости имели опознавательные обозначения, позволявшие со-

блюдать и учитывать порядок следования добытых ими чисел даже при одно-

временном метании. Эти знаки — изображения горшка, диска и слона (сим-

волов удачи). Если бы эта система была положена в основу игры, можно было

бы констатировать новую, восьмую стадию эволюции игры. Но для игры это

новшество оказалось слишком громоздким, и даже в практику оракулов оно

глубоко не внедрилось.

Правда, в обоих сочинениях, донесших до нас подробные описания ора-

кульной практики метания костей (в рукописи Бау и в Пашакакевали), приве-

дены (с названиями) все 64 позиции, но в подоснове можно разглядеть иную

ситуацию. Текст рукописи Бау выглядит строже и сохраннее. В Пашакакевали

только 18 позиций названы теми же словами, что в рукописи Бау, еще несколь-

ко терминов близки названиям в той рукописи по звучанию, многие термины

расширили свое значение, распространившись на смежные позиции, есть не-

сколько совсем новых названий, а ряд позиций не назван вовсе — видимо,

названия утрачены. Похоже, что текст отражает несколько иную традицию,

а вдобавок попорчен.

Однако, хоть в обоих текстах перечисляются 64 позиции, тем не менее,

названия тех позиций, которые различаются только перестановкой цифр,

одни и те же, т. е. неоднократно повторяются. Иначе говоря, названиями об-

ладают, собственно, не эти позиции, а только сочетания чисел. Перестановки

же в номенклатуре не учитываются. Их учет еще не успел вызвать перестрой-

ку номенклатуры.

Это особенно хорошо видно по рукописи Бау. Здесь, если слить повторе-

ния, не 64 названия, а ровно 20 (сохранилось 19, три четверки отсутствуют).

Вот они (рис. 120).

Все это означает, что учет перестановок — новшество, что в номенкла-

туре отражена более древняя система восприятия выпадений, что эта тра-

диционная система не учитывала перестановок и ограничивалась 20 комби-

нациями. Она вполне соответствовала предусмотренным выше параметрам

последней стадии эволюции игры.

9. Игра с лесным духом и богиней. Система получения и преобразова-

ни^случайных чисел, которую мы застаем в описаниях оракулов, оказалась

IX. Игры с богами

349

№

Сочетания

Название в

MSBow

Перевод Название в Перевод

Pasakakevali

111

kalaviddhi

Sobhana

2 112 khan

ослица kartarl, gurdabhT

113

cuiicuna

ciftcini

114 karna

kamika

5 122

paftcT

vasa, pattff

6 123

dundubhi

7 124

bhadra

удача bhadra удача

8 133 kana

manthin

9 134 sakti"

копье satti, vijaya

144

kuta

vrsa бык

11 222

pattabandha

— . . ,„

12 223 saja

kuta .,"

224

presya praSna

233

vitf

dundubhi, tripadr

234

vahula

bahula, saphala корова,...

16 244 vrsa

бык vrsa бык

17 333 navikkT

—

18 334

mair

венец, коро- malim, marjanT

на, гирлянда

344

sapata павлин sakatf

Рис. 120. Названия сочетаний в индийской игре в кости

(Клейн, 1987; Klejn, 1999)

неоднородной, в ней удалось освободить от позднейших наслоений параме-

тры седьмой стадии эволюции игры. Но с предшествующими (катакомбными)

эта стадия, при всей разительности сходства некоторых деталей (три кости

в наборе, четырехгранность костей), пока что увязывается лишь чисто логиче-

ски — хорошо приходится на то место, куда мысленно мы продолжаем траек-

торию развития причерноморской игры бронзового века.

Но в индийской традиционной игре в кости «пашака» есть и более жесткие

конкретные зацепки для ретроспективной привязки ее к катакомбной игре.

326

326 Лев Клейн. ВРЕМЯ КЕНТАВРОВ

В позднесредневековом прозаическом сочинении Видхурапандитаджа-

таке (VI, 280,1 сл.) рассказывается об игре царя народа Куру с лесным духом

Пуннакой. Событие относится к ведическим временам. Пуннака вызвал царя

на игру в кости. Условились, на что играют; приготовили золотые кости на

серебряной доске. Собралось множество знатных зрителей.

Пуннака обратился к царю с речью, и далее диалог в тексте джатаки из-

лагается так:

«„Махараджа, при игре в кости есть двадцать четыре так называемых

ayas: mali, savata, bahula, santi, bhadra и т.д. Выбери себе из них один ауа,

который тебе нравится". — „Хорошо", — сказал царь и выбрал bahula; Пун-

нака выбрал savata. Затем царь сказал ему: „Ну же, мой дорогой юный друг,

бросай кости". — „Махараджа, сперва не мой черед, бросай ты". — „Хоро-

шо", — сказал царь, согласившись».

Перед тем как приступить, он обратился с традиционным песенным гим-

ном к покровительствовавшей ему богине, моля о ниспослании победы. Он

пел:

«О богиня, ниспошли мне победу. Смотри, как мало у меня счастья...

Восьмерка называется malika, а шестерка идет как savata. Четверка обозна-

чается bahula, а состоящая из двух родственных — badraka. И двадцать че-

тыре ayas объясняются превосходным мудрецом: malika, оба kakas, savata,

mandaka, ravi, bahula, nemi, sanighatta, santi, bhadra и titthira».

Он пел эту песню, перекатывая кости в руке, а затем бросил их в воз-

дух. Из-за колдовства Пуннаки они летели неудачно. Царь подметил это

и с помощью богини поймал их на лету и бросил еще раз. Но они снова лете-

ли неудачно. Он снова поймал их. Тут Пуннака подглядел, что царю помогает

богиня. Он уставился на нее, та испугалась его взгляда и убежала. В третий

раз царь не сумел поймать кости на лету, и они выпали неудачно. Бросил

Пуннака — и выиграл.

В этом рассказе мы узнаем игру с загаданными комбинациями (ayas).

Узнаем и некоторые известные по оракулам названия комбинаций: malika

(mali), bahula (vahula), savata (sapata), bhadra; остальные в оракулах отсут-

ствуют. Странным представляется количество комбинаций — 24. Оно странно

не потому, что в песне названы только 12 — что ж, остальные могли остаться

неупомянутыми. Странно потому, что ни в системе оракулов, ни в более ран-

них системах (новосвободненской и катакомбных) перечень в 24 комбинации

никак не получается, в 12 — тоже.

Большие Причерноморские наборы дают по 20 комбинаций (без нуле-

вых — по 1^), с перестановками — по 64, малый Никопольский набор дает

10 комбинаций (без нулевых чисел — 9), с перестановками — 16. Суммарных

IX. Игры с богами 176

350

чисел в новосвободненских наборах — 15 (без нулевого — 14), в больших

катакомбных — 17 (без нулевого — 16), в Никопольском — те же 10 (9).

Напрашивается вывод, что учитывались не все перестановки или даже не

все комбинации, не все получали название. Подобную смешанную систему на-

ходим в китайской игре с кубическими костями «Чак Цин кау» («Метать небеса

и девятки»), возводимой в конечном счете к индийским образцам (характерна

и «правильная» разметка кубиков). В игре участвуют 2 кубика, стороны их раз-

мечены цифрами от 1 до 6 (причем 1 и 4 — красные, а 1 — еще и больше других),

получается 21 комбинация без учета перестановок. Особые названия есть лишь

у комбинаций из одинаковых чисел: две шестерки (бб) называются «Небо» (это

наибольшая удача), две единицы (11) — «Земля», две четверки (44) — «Чело-

век», две пятерки (55) — «Цветок Сливы», две двойки (22) — «Скамья», и только

две тройки (33) — это всего лишь «Длинные тройки». Комбинации из разных

цифр выступают в виде сумм и, соответственно, именуются (скажем 54 или

63 — «девятки», и т. п.). Впрочем, некоторые из таких суммарных чисел отли-

чаются особыми эпитетами от таких же другого состава (из других слагаемых):

46 — «десятка с Красной Головой», 16 — «семерка с Длинной Ногой», 15 —

«шестерка с Красной колотушкой» (все это по внешнему облику цифр), но так-

же 13 — «Гармония», 56 — «Голова тигра». Все 11 комбинаций с особыми сло-

весными названиями составляют группу «чан» («штатские»), все 10 оставшихся

с чисто числовыми названиями — группу «мо» («военные»).

Таким образом, главное деление проходит между комбинациями из оди-

наковых цифр и комбинациями из разных цифр (последние преимуществен-

но суммируются, а не именуются). Это действительно важное деление: ком-

бинации из одинаковых цифр лишены возможности перестановок и имеют

наименьшие шансы выпадения. Интересно взглянуть под этим углом зрения

на индийскую систему комбинаций, получаемую при метании трех четырех-

сторонних костей с цифрами 1, 2, 3,4 на сторонах (на рис. 119 система комби-

наций упорядочена именно в этом плане).

И правда, здесь четыре самых разнородных комбинации, т. е. те, у ко-

торых все цифры разные (группа С на рис. 119), если их учитывать со всеми

перестановками, дадут 24 позиции, а если отбросить четыре однородных

комбинации, т. е. состоящие из одинаковых цифр (группа А), то оставшихся

комбинаций (группа В) как раз 12. Но названия, упомянутые в песне, распре-

деляются по обеим группам: bhadra и vahula — в группе С, mali и sapata —

в группе В. Приходится признать, что нам непонятен способ, которым от-

бирались (из принципиально возможных) учитываемые в игре комбинации,

известные царю Куру и Пуннаке, и нам не хватает данных, чтобы этот способ

определить.

326

326 Лев Клейн. ВРЕМЯ КЕНТАВРОВ

Однако обратимся к гимну, который, в силу своего ритуального характера

и жесткой фиксированности (стихи, гаты), должен считаться гораздо более

древним, чем включающий его рассказ джатаки. В этом гимне содержатся яв-

ные указания на то, что названия комбинаций генетически связаны с некими

числами и что в предыстории индийской игры в кости был этап, когда имело

значение суммирование очков. Более того — что особенности игры на этом

давнем этапе совпадают с катакомбными.

В самом деле, malika и savata оказываются названиями не сочетаний

(3-3-4 и 3-4-4), как в оракулах, а чисел 8 и б, причем на индийских костях каж-

дое из них может быть только суммой (или порядковым номером), а первое из

них и в катакомбном обиходе могло быть только суммой. И это совсем те же

суммы, которые получаются от чисел из оракулов. Существенно, что оба назва-

ния выделены в песне — названы первыми. В числовых системах оракулов для

этого нет никаких оснований. Но такие основания есть в катакомбной системе

больших наборов: шестерка и восьмерка принадлежали к тем немногим (трем)

суммам, которые имели удвоенные возможности образования и, следовательно,

по тогдашним соображениям, должны были чаще приносить удачу. Третьим та-

ким числом было двенадцать, выпадавшее в виде двух шестерок или трех четве-

рок. Не оно ли имеется в виду под bhadraka, состоящим «из двух родственных»?

В гимне также выделена (хотя и после восьмерки и шестерки) четверка,

не имевшая удвоенных возможностей образования. Но это — число, обла-

давшее сакральным значением не только в культурах, родственных шнуровой

керамике, не только в раннегерманской и, может быть, в степном иранском

мире, но и в Индии, особенно сопряженное там с представлениями об удаче:

во второй из главных индийских игр в кости — игре в aksas (акши, вибхидака,

бабхру — индийское соответствие альчикам) — делимость количества выпав-

ших костей на четыре была критерием победы, выигрыша (обозначавшегося

словом «крита» — krta).

В игре катакомбного типа с большим набором костей удачливость чет-

верки была кажущейся. Царь Куру выбрал bahula — четверку — и проиграл.

Пуннака выбрал savata — шестерку — и выиграл. Немудрено: у него было

вдвое больше шансов (ср. рис. 119), если, конечно, герои джатаки играли

в игру, сохранившую разметку костей и частично правила, унаследованные от

катакомбной культурной общности.

10. Доля царя. Вернемся к самой древней находке игральных костей —

новосвободненской каменной гробнице в кургане, раскопанной А. Резепки-

ным в Кладах, с женщиной и ребенком. У головы ребенка лежали два набора

для игры в кости.

IX. Игры с богами 177

352

Напомню, каждый набор в Кладах состоит из трех костей и трех пало-

чек (одна была еще до погребения утеряна, и для подмены на одной кости

дополнительно нанесена разметка, как на палочке). Игральные кости име-

ют вид не кубиков, как современные, а продолговатых граненых бус, су-

жающихся к концам. У них не шесть сторон, а только четыре. Знаки на этих

сторонах — цифры, древнейшие в мире! Значения их ясны: пусто, единица,

тройка и шестерка — шесть рисок, сгруппированных попарно, как в египет-

ском иероглифе «шесть».

Метнув все три кости, можно было в случае удачи получить максималь-

ный выигрыш: три шестерки, то есть восемнадцать. А на палочках разметка

другая: пусто, единица, четыре и восемнадцать. Таким образом, удачное по-

ложение деревянной или серебряной палочки сразу давало восемнадцать —

максимальный выигрыш костями. Более высокое положение палочек подчер-

кивается их изготовлением (в однм наборе) из серебра.

Находка эта заставляет еще раз обратить свой взор к Древней Индии. Не

только потому, что у индоариев игра в кости была чрезвычайно популярна.

Я уже отмечал, что в Ригведе есть даже «Гимн Игрока» («Жалоба Игрока»).

И не только потому, что в индийской игре надо было метать три кости, и ко-

сти эти были четырехгранными — чатурашра! Здесь я хочу подчеркнуть дру-

гое. Число 18 было в Индии благотворным и предпочитаемым. В Махабхарате

восемнадцать книг, и воспеваемая в ней битва продолжалась восемнадцать

дней. В царском жертвоприношении белого коня (ашвамедхе) вместе с этим

священным конем погребали еще множество коней, располагая их у 20 ко-

новязей группами по 18 коней в каждой. На Западном Кавказе эта традиция

продолжалась и в скифское время — двадцатью группами по восемнадцать

лежали скелеты лошадей в раскопанном Веселовским Ульском кургане скиф-

ского времени, на две тысячи лет позже Новосвободной.

В царской могиле игральные кости оказались не случайно. Первоначально

царская власть не была наследственной. Цари избирались по жребию — счита-

лось, что так можно угадать божью волю. А жеребьевка проводилась метанием

игральных костей — царство нужно было выиграть у предшествующего царя.

Об этом времени напоминают многочисленные легенды о выигранных и прои-

гранных царствах. В Махабхарате Наль проиграл свое царство, но отказался

сыграть на свою жену царицу Дамаянти, а потом удачной игрой вернул царство.

Царь Юдиштхира проиграл свое царство и царицу, но проигранное вернул вой-

ной — именно эта битва продожалась 18 дней, а участвовало в ней 18 армий.

Как рудимент прежних порядков в позднее время при коронации царя прово-

дилась игра в кости; царь играл с одним из сородичей, и (тут уж сородичу по-

лагалось вести себя умно) царь непременно выигрывал.

326

326 Лев Клейн. ВРЕМЯ КЕНТАВРОВ

В новосвободненской гробнице оба игральных набора лежат у головы

ребенка. По-видимому, этот отпрыск царского рода еще не царствовал, и по

справедливости в загробном существовании ему еще предстояло то, что он не

успел совершить в земной жизни: он должен был хотя бы на том свете сыграть

и выиграть свое царство. Но почему наборов два? Возможно, покойному суж-

дено было, как легендарному Налю, играть на царство дважды.

Возможно, однако, что вторым набором он должен был выиграть не

царство, а нечто иное. Дело в том, что и рядовые индийцы проходили через

обряды, в которых имитировалась игра в кости. В этих обрядах участвовал

в качестве главной фигуры младший сын хозяина, а разыгрывалась его, млад-

шего, доля, его удел, его участь, его счастье, кстати, все эти русские слова

образованы от корней, смысл которых: «делить», «часть». Жизненной долей

наделяло с помощью случайной удачи в игре божество. Понятие «доля» в ин-

доиранских языках обозначалось словом «бхага», «бага», от которого (через

скифов и сарматов) происходит славянское «богъ».

Первоначально у славян бог обозначался иначе (как и в других индоевро-

пейских — лат. «деус», русск. «див»), а заимствованное у иранцев-сарматов

слово «бог» означало «благую долю». Это застряло в производных словах.

«Усатый» значит'обладающий усами', «горбатый» — 'с горбом', «чреватый» —

'с чревом', «рогатый» — 'с рогами', но «богатый» — это ведь не 'обладающий

богом' или 'богами' и уж никак не 'богатством' — это слово вторичное, оно

производно от «богатый». По первоначальному смыслу «богатый» — это 'тот,

у которого благая доля', 'у которого большая доля'. Соответственно, противо-

положный смысл у слова «убогий». «Утлый челнок» — это 'суденышко без

«тла»', то есть 'без дна' или 'с плохим дном'. Но «убогий» — это не 'лишенный

бога', это 'лишенный благой участи', или просто 'лишенный доли'. Украинское

«небога» значит 'несчастный'. По-белорусски «небожчик» значит 'покойник'.

Во всех этих словах с корнем «бог» просвечивает старый смысл этого корня:

'лучшая доля', 'благая участь', 'завидная судьба'.

Игра в кости была также популярна у древних греков и германцев. Па-

трокл за игрой в кости убил своего родича и потому лишился родины и бежал

к семейству Ахилла. На многих древних изображениях можно видеть Ахилла,

играющего в кости с Аяксом (по преданию, они настолько увлеклись игрой, что

не слышали нападения амазонок). Германцам, по рассказу Тацита, игра в кости

представлялась делом чрезвычайной важности. Перед началом ее они пости-

лись, а проигравшись в пух и прах, ставили на свою свободу — проигравший

становился рабом того, кто выиграл. Похоже, что игра у них регламентирова-

лась теми Ле традициями, что у индоариев, и проистекала из того же источни-

ка. Число 18 обладало и у германцев магическим смыслом: в «Старшей Эдде»

IX. Игры с богами 178

354

Рис. 121. Крюкастые вилы новосвободненского типа

из ст. Псебайской (по А. А. Иессену, 1935)

самое древнее — это

18 заклинаний Всеот-

ца Одина, 18 вопро-

сов Одина и ответов

Вафтруднира. У Халь-

вдана Старшего было

18 сыновей, половина

из них — основатели

рода Нибелунгов. При-

частны к этим тради-

циям и кельты — у них

был в древности воем-

надцатиричный счет.

Игре в кости у ин-

доариев покровитель-

ствовал однорукий бог Савитар, у германцев — однорукий бог Тиу. Когда-то,

у истоков игры, бог с одной рукой стал ее символом по понятной, но доста-

точно оригинальной идее: левая сторона (и левая рука) ассоциируется с не-

хорошими делами, с неудачей, а для метания костей вторая рука вообще не

нужна — удача, по Ригведе, в руке, пусть у бога останется только та рука, в ко-

торой удача. Так что у «одноруких бандитов» — игральных автоматов были

древние прообразы в лице одноруких богов.

В той же Новосвободненской гробнице есть и еще находки, связанные

с определением доли. Это две бронзовые крюкастые вилы, похожие на русские

печные ухваты (рис. 121, есть и в Кладах). Таких находок много в погребениях

новосвободненского типа, но только в богатых. Иногда они снабжены литыми

фигурками каких-то героев, а зубья-крючья похожи на рога майкопских бы-

ков (рис. 121, илл. 38). Назначение этих вил определили давно. Это инстру-

менты для доставания мяса из огромных пиршественных котлов — поэтому

они есть только в могилах знати, которая могла задавать «пир на весь мир».

В половине случаев вместе с вилами в погребениях найдены и медные котлы.

Вилы упоминаются в нартском эпосе кабардинцев — там говорится, как один

из нартов «воткнул в котел огромную двурогую вилку и достал оттуда целую

ногу быка». Абхазы до недавнего времени пользовались такими же вилами,

вынимая мясо из котлов.

Но более важную социальную функцию этих вил выяснил венгерский ар-

хеолог Янош Маккай. Вилы эти, как оказалось, распространены были в древ-

ности у многих народов, главным образом у индоевропейских. Не всегда

У этих вил по два зубца — иногда три или пять. Трехзубая вила — таков ведь,

179

Лев Клейн. ВРЕМЯ КЕНТАВРОВ

по сути, трезубец Посейдона, перешедший в римской символике к Нептуну.

Принимать его за острогу для ловли рыбы нельзя: Посейдон в древнейшей

греческой мифологии не был богом моря. Пятизубцами у Гомера снабжены

юноши, приносящие жертву Аполлону. Что связывает эти инструменты с бога-

ми и жертвоприношениями?

Проясняет это цитата из Библии. Евреи — один из немногих народов,

не относящихся к индоевропейской семье, но всё же применявших эти вилы

(впрочем, у евреев есть индоевропейская примесь с добиблейского време-

ни — от миграции индоевропейских «народов моря» в XIII-XII вв. в Палести-

ну). «Обычай жреца в народе, — сообщает книга Самуила, — был шуровать

мясным крюком о трех зубьях; и вот он сунет его в сковороду, или чугунок,

или котел, или горшок; всё, что мясной крюк извлечет, жрец берет себе»

(I Сам. 2,13-14). Это была доля жреца'. Жрецы же, конечно, утверждали свои

притязания и права на первую долю во всём как слуги и воплощения богов.

В конечном счете вилы-крючья направлялись рукой бога — Яхве, Посейдона,

Аполлона. Ригведа воспевает Индру, который хватает свою жертву крюком.

Доля младшего сына была по ритуалу проигрышной (причина такого на-

меренного проигрыша — сложная проблема, потому что у многих народов

именно младшему сыну доставалось главное наследство). Доля царя была,

разумеется, львиной долей. Но с нею всегда спорила доля жреца, неотличи-

мая от доли бога.

X. Тропой единорога

Тут взгляд Единорога упал на Алису.

Он круто повернулся и стал разглядывать ее с явным отвращением.

— Да что это такое? — спросил он наконец.

— Это дитя, — тотчас ответил Зай Атс,

вскочив, чтобы представить Алису... — Мы нашли его только сегодня.

—А я-то всегда думал, что все они сказочные чудища! — заметил Единорог.

— Оно настоящее, живое?

— Да-а! И к тому же говорящее! — важно ответил Зай Атс.

Единорог задумчиво посмотрел на Алису и проговорил:

— Ну, скажи что-нибудь, дитя.

Не в силах удержаться от улыбки, Алиса на это ответила:

— Вы знаете, я тоже всегда думала, что Единороги — сказочные чудища.

Я никогда не видела живого Единорога.

— Ну что ж, теперь мы увидели друг друга, — сказал Единорог, тоже

улыбаясь.

— Я верю, что ты есть на самом деле, если ты поверишь, что есть я. Идет?

Л. Кэролл. Алиса в Стране Чудес. Гл. XI.

1. Головы без тела, скипетры без царей. Как археолог я люблю серий-

ные вещи. А то ведь найдется одна — странная, непонятная, черт-те что, но

интересная своей заковыристостью. Манит и манит, не оторваться. Начинаешь

подыскивать аналогии, одна к одной — долгая, утомительная, но азартная ра-

бота. Дождешься, что лягут они на карту густой россыпью. Серия. Сопутству-

ющие находки очертят хронологию, что-то расскажут о месте в культуре —

уже кое-что знаешь, но всё еще информация скудная и прибавляется очень

скупо. А потом яркая, полная

находка впишется в эту се-

рию — и всё вдруг осветится

и заиграет. А бывает, и просто

озарение — невесть откуда,

наитие. И уж тогда откры-

тия пойдут цепной реакцией,

только поспевай записывать.

Так происходит не только

в биографии ученого, но и в

истории науки.

Восемьдесят лет назад,

в 1928 г., в этнографический

отдел Русского музея в Ле-

нинграде (позже выделился

в Музей этнографии) была

Доставлена странная наход-

Рис. 122. Каменное изваяние из Терекли-Мектеба —

а каменное изваяние ГО- ф

0Т0 и

рисунок в трех ракурсах (по А. А. Иессену, 1952,

ЛОВЫ ЖИВОТНОГО (рис. 122). И В. А. Дергачеву, 2007)