Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


61
Розділ I. Лінійна та векторна алгебра
Фундаментальна система розв’язків одержується, якщо вільним
змінним х
2
, х
3
послідовно надати значення х
2
= 1, х
3
= 0; х
2
= 0, х
3
= 1:
X
1
=
0
1
0
§·
¨¸
¨¸
¨¸
©¹
; X
2
=
1
0
1
§·
¨¸
¨¸
¨¸
©¹
.
Одержали два лінійно незалежні власні вектори. Уся сукупність
векторів, що відповідають власному значенню
1
O
= 1 має вигляд:
1
X
O
=
0
1
0
§·
¨¸
¨¸
¨¸
©¹
С
1
+
1
0
1
§·
¨¸
¨¸
¨¸
©¹
С
2
, С
1
, С
2
R, |С
1
| + |С
2
|
z
0.
2)
2
O
= 3, r = 1:
13
123
13
(2 ) 0,
(1 ) 0,
(2 ) 0.
xx
xxx
xx
O
O
O
°
®
°
¯
13
123
13
0,
20,
0.
xx
xxx
xx
°
®
°
¯
Фундаментальна система розв’язків одержується, якщо покласти
х
3
= 1:
1
12
3
1,
21,
1,
x
xx
x
°
®
°
¯
1
2
3
1,
1,
1,
x
x
x
°
®
°
¯
X
3
=
1
1
1
§·
¨¸
¨¸
¨¸
©¹
.
3
X
O
=
1
1
1
§·
¨¸
¨¸
¨¸
©¹
С, С
R, С
z
0.

62
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
1.7.3. Завдання для самостійної роботи
Знайти власні вектори і власні значення матриці А:
1.92.
11
24
§·
¨¸
©¹
. 1.93.
12
21
§·
¨¸
©¹
.
1.94.
32
43
§·
¨¸
©¹
. 1.95.
11 1
010
11 1
§·
¨¸
¨¸
¨¸
©¹
.
1.96.
122
224
24 2
§·
¨¸
¨¸
¨¸
©¹
. 1.97.
212
533
10 2
§·
¨¸
¨¸
¨¸
©¹
.
1.98. Знаючи характеристичні числа матриці А, знайти характе+
ристичні числа матриці А
–1
.

63
Розділ I. Лінійна та векторна алгебра
§1.8. Квадратичні форми
1.6.1. Теоретичні відомості
Однорідний многочлен другого степеня відносно змінних х
1
, х
2
Ф(х
1
, х
2
) = а
11
2
1
x
+ 2а
12
х
1
х
2
+ а
22
2
2
x
, (1.26)
називається квадратичною формою від цих змінних. Якщо покла+
сти а
21
= а
12
, то квадратичну форму (1.26) можна записати у вигляді:
Ф(х
1
, х
2
) = х
1
(а
11
х
1
+ а
12
х
2
) + х
2
(а
21
х
1
+ а
22
х
2
),
або
Ф = х
1
у
1
+ х
2
у
2
, (1.27)
де
1111122
2211222
y
ax ax
y
ax ax
®
¯
. (1.28)
Вираз (1.28), а отже і квадратична форма (1.26) повністю визна+
чається матрицею А =
11 12
21 22
aa
aa
§·
¨¸
©¹
, яка називається матрицею квад,
ратичної форми (1.26).
Здійснюючи заміну базису, квадратичну форму (1.26) можна
привести до виду:
Ф(у
1
, у
2
) =
2
11
y
O
+
2
22
y
O
, (1.29)
де у
1
, у
2
— нові змінні, що лінійно виражаються через х
1
, х
2
(1.28);
1
O
,
2
O
— власні значення матриці А.
Вираз (1.29) називається канонічним видом квадратичної фор,
ми (1.26).
Розглянемо квадратичну форму Ф(X), де А – матриця коефіцієнтів
А =
11 12 1
21 22 2
12
...
...
... ... ... ...
...
n
n
nn nn
aa a
aa a
aa a
§·
¨¸
¨¸
¨¸
¨¸
©¹
, X =
1
2
...
n
x
x
x
§·
¨¸
¨¸
¨¸
¨¸
©¹
, X
Т
=(х
1
, х
2
, ... , х
n
).

64
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
1.8.2. Розв’язання прикладів
Приклад 1.99. Квадратична форма
Ф
1
(X) = Ф(х
1
, х
2
, х
3
) =
2
1
x
+ 2
2
2
x
+ 3
2
3
x
є додатно визначеною.
Квадратична форма
Ф
2
(X) = Ф(х
1
, х
2
, х
3
) = (х
1
– х
2
)
2
+ (х
2
– х
3
)
2
є невід’ємною.
Квадратична форма
Ф
3
(X) = Ф(х
1
, х
2
, х
3
) =
2
1
x
+
2
2
x
–
2
3
x
є невизначеною.
Квадратична форма
Ф
4
(X) = Ф(х
1
, х
2
) = –3
2
1
x
+ 4х
1
х
2
– 2
2
2
x
є від’ємною визначеною.
Приклад 1.100. Використовуючи теорію квадратичних форм,
привести до канонічного виду рівняння лінії другого порядку
4х
2
+ 24ху + 11у
2
= 20.
Розв’язок. Рівняння лінії запишемо у вигляді 4х
2
+2
12ху+11у
2
=20,
в якому а
11
= 4, а
12
= а
21
= 12, а
22
= 11.
Складемо характеристичне рівняння матриці А =
412
12 11
§·
¨¸
©¹
і знай+
демо її власні значення.
Тоді квадратичну форму можна записати так:
Ф(X) = X
Т
АX. (1.30)
Квадратична форма Ф(X) називається додатно визначеною, якщо
для всіх дійсних значень X
z
0 виконується нерівність Ф(X)>0, і
невід’ємною, якщо для всіх дійсних значень X
z
0 виконується
нерівність Ф(X)
t
0.
Якщо Ф(X) додатно визначена, то квадратична форма –Ф(X)
називається від’ємно визначеною. Якщо квадратична форма Ф(X)
може набувати від’ємних і додатних значень, то вона називається
невизначеною.

65
Розділ I. Лінійна та векторна алгебра
412
12 11
O
O
= 0, або
2
O
– 15
O
– 100 = 0.
Корені рівняння
1
O
= 20,
2
O
= 5 є власними значеннями. Отже,
рівняння лінії перетворюється до виду 20(
x
c
)
2
– 5(
y
c
)
2
= 20, або
2
(')
1
x
–
2
(')
4
y
=1. Одержана лінія — гіпербола.
Властивості квадратичної форми (1.30) пов’язані з власними чис+
лами матриці А.
Приклад 1.101. Привести до канонічного виду рівняння лінії
17х
2
+12ху+8у
2
–20=0.
Розв’язок. Група старших членів цього рівняння утворює квадра+
тичну форму 17х
2
+12ху+8у
2
. Її матриця А =
17 6
68
§·
¨¸
©¹
.
Власними значеннями будуть числа
1
O
= 5,
2
O
= 20. Отже, квад+
ратична форма 17х
2
+12ху+8у
2
перетворюється до виду 5(
x
c
)
2
+
+20(
y
c
)
2
, а дане рівняння — до виду 5(
x
c
)
2
+ 20(
y
c
)
2
— 20 = 0, або
2
(')
4
x
+
2
(')
1
y
= 1. Це є еліпс.
1.8.3. Завдання для самостійного розв’язку
Перетворити до суми квадратів квадратичні форми:
1.102.
22 2
1122233
2245xxxxxxx
.
1.103.
222
1121323
424xxxxxxx
.
1.104.
12 23 31
xx xx xx
.
1.105.
2222
1 12 13 14 2 23 24 3 4
222 24 2x xx xx xx x xx xx x x
.
1.106.
2
11234
xxxxx
.
66
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§1.9. Застосування матричного числення при розв’язанні
економічних задач
1.9.1. Розв’язання прикладів
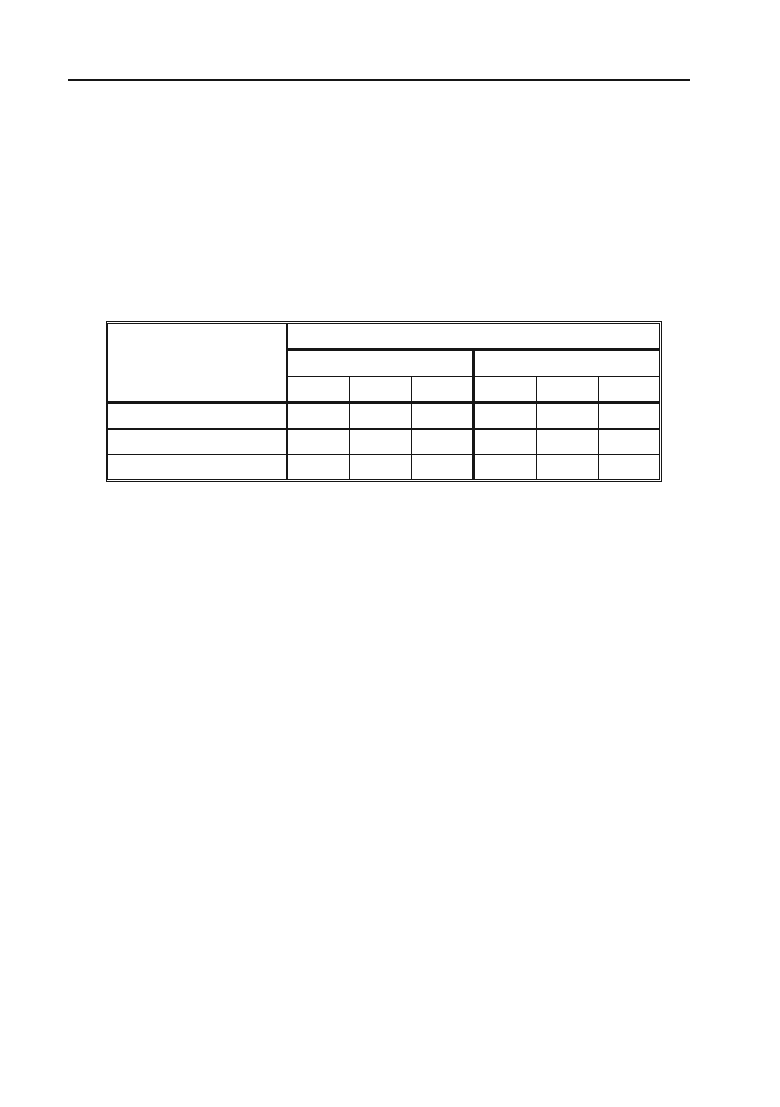
Приклад 1.107. Два залізобетонних заводи випускають вироби
M, N, P вищої, першої та другої категорії якості. Кількість випуще+
них кожним заводом виробів за кожною категорією якості характе+
ризується наступною таблицею:
Який загальний випуск виробів за означеними категоріями
якості?
Розв’язок. Кількість виробів, випущених першим заводом, можна
розглядати як елементи матриці А, а другим заводом — як елементи
матриці В:
А =
150 240 320
100 130 175
25 15 20
§·
¨¸
¨¸
¨¸
©¹
; В =
280 300 450
120 150 170
30 20 18
§·
¨¸
¨¸
¨¸
©¹
.
Додавши їх, отримаємо матрицю С, яка визначає загальне число
виробів за означеними категоріями якості:
С = А + В =
430 540 770
220 280 345
55 35 38
§·
¨¸
¨¸
¨¸
©¹
.
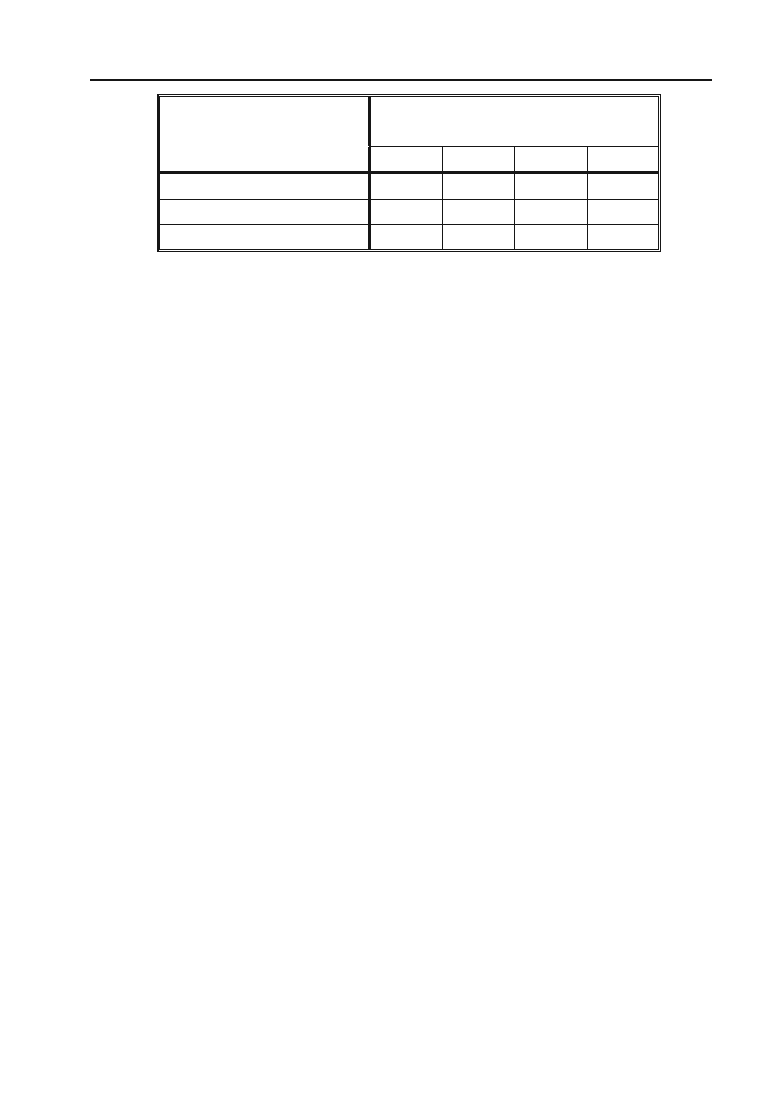
Приклад 1.108. При виготовленні деталей чотирьох видів вит+
ратних матеріалів, робочої сили та електроенергії задаються наступ+
ною таблицею (в умовних одиницях):
Готові вироби
І завод ІІ завод
Категорія якості
M N P M N P
Вища 150 240 320 280 300 450
Перша 100 130 175 120 150 170
Друга 25 15 20 30 20 18
67
Розділ I. Лінійна та векторна алгебра
Обчислити загальну потребу в матеріалах у
1
, робочій силі у
2
та
електроенергії у
3
, для виготовлення заданої кількості деталей кож+
ного виду: х
1
= 10; х
2
= 2; х
3
= 8; х
4
= 4.
Розв’язок. Загальна потреба в матеріалах, робочій силі та елект+
роенергії для виготовлення кількості х
і
(і = 1, ..., 4) деталей одного
виду визначається рівнянням Y = АX, де
Y =
1
2
3
4
y
y
y
y
§·
¨¸
¨¸
¨¸
¨¸
©¹
— матриця загальної потреби в ресурсах;
А =
130,52
1, 5 2 3 1
2110,5
§·
¨¸
¨¸
¨¸
©¹
— матриця норм витрат ресурсів;
X =
1
2
3
4
х
х
х
х
§·
¨¸
¨¸
¨¸
¨¸
©¹
— матриця кількості виробів (за видами).
При X =
10
2
8
4
§·
¨¸
¨¸
¨¸
¨¸
©¹
із рівняння Y = АX отримаємо:
Витрати на одну деталь
кожного виду
Ресурси
1 2 3 4
Матеріали 1 3 0,5 2
Робоча сила 1,5 2 3 1
Електроенергія 2 1 1 0,5
68
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Y =
1
2
3
4
y
y
y
y
§·
¨¸
¨¸
¨¸
¨¸
©¹
=
130,52
1, 5 2 3 1
2110,5
§·
¨¸
¨¸
¨¸
©¹
10
2
8
4
§·
¨¸
¨¸
¨¸
¨¸
©¹
=
28
47
32
§·
¨¸
¨¸
¨¸
©¹
,
тобто для виготовлення заданої кількості деталей кожного виду не+
обхідно 28 одиниць матеріалів, 47 одиниць робочої сили, 32одиниці
електроенергії.
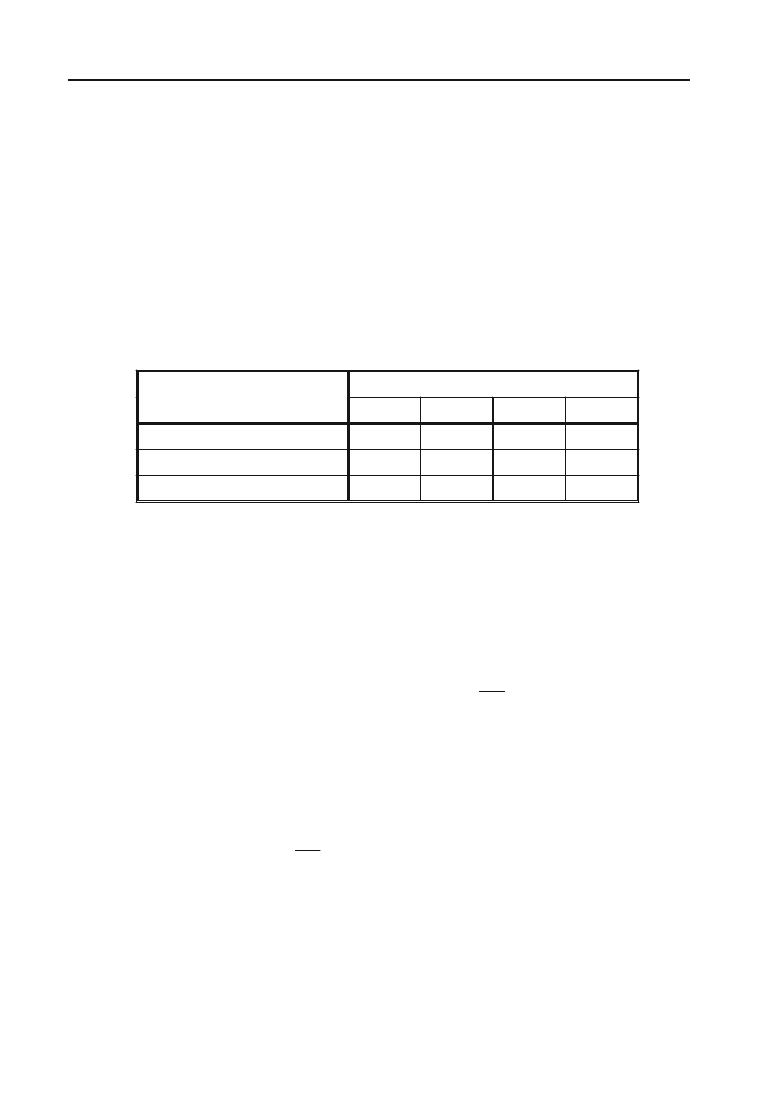
Приклад 1.109. У наступній таблиці у вибраних одиницях наве+
дено склад вітамінів в харчових продуктах П
1
, П
2
, П
3
:
1. Скільки вітамінів кожного виду міститься в раціоні, що включає 5
одиниць продукту П
1
, 10 одиниць продукту П
2
і 8 одиниць продукту П
3
?
2. Враховуючи тільки вартість вітамінів у кожному продукті з
розрахунку відповідно 10, 20, 25 і 50 грош. од. за одиницю кожного
виду продукту.
3. Підрахувати вартість раціону, склад якого наведено у п. 1.
Розв’язок. Введемо такі позначення: А = (5 10 8), а
1і
— кількість
одиниць продукту і+того виду в раціоні, і =
1, 3
;
В =
0,5 0,5 0 0
0,3 0 0,2 0,1
0,1 0,1 0,2 0,5
§·
¨¸
¨¸
¨¸
©¹
, b
ij
— кількість вітамінів jго виду в
одиниці і+того виду, j =
1, 4
;
С =
10
20
25
50
§·
¨¸
¨¸
¨¸
¨¸
©¹
, с
j1
— вартість одиниці вітаміну j+того виду.
Вітаміни
Продукти
А В С D
П
1
0,5 0,5 0 0
П
2
0,3 0 0,2 0,1
П
3
0,1 0,1 0,2 0,5

69
Розділ I. Лінійна та векторна алгебра
1. Позначимо D =
11
21
31
41
d
d
d
d
§·
¨¸
¨¸
¨¸
¨¸
©¹
, d
j1
— кількість вітамінів j+того виду,
що містяться в раціоні. Тоді АВ = D.
D = (5 10 8)
0,5 0,5 0 0
0,3 0 0,2 0,1
0,1 0,1 0,2 0,5
§·
¨¸
¨¸
¨¸
©¹
=
2,530,8
2,5 0, 8
21,6
14
§·
¨¸
¨¸
¨¸
¨¸
©¹
=
6,3
3,3
3,6
5
§·
¨¸
¨¸
¨¸
¨¸
©¹
.
2. Позначимо
F =
11
21
31
f
f
f
§·
¨¸
¨¸
¨¸
©¹
, f
i1
— вартість одиниці продукції і+того
виду і =
1, 3
. Тоді F = ВС.
F =
0,5 0,5 0 0
0,3 0 0,2 0,1
0,1 0,1 0,2 0,5
§·
¨¸
¨¸
¨¸
©¹
10
20
25
50
§·
¨¸
¨¸
¨¸
¨¸
©¹
=
510
355
12525
§·
¨¸
¨¸
¨¸
©¹
=
15
13
33
§·
¨¸
¨¸
¨¸
©¹
.
3. Позначимо через S — вартість раціону, склад якого наведено у
п. 1.
Тоді S = A
F.
S = (5 10 8)
15
13
33
§·
¨¸
¨¸
¨¸
©¹
= 75 + 130 + 264 = 469.
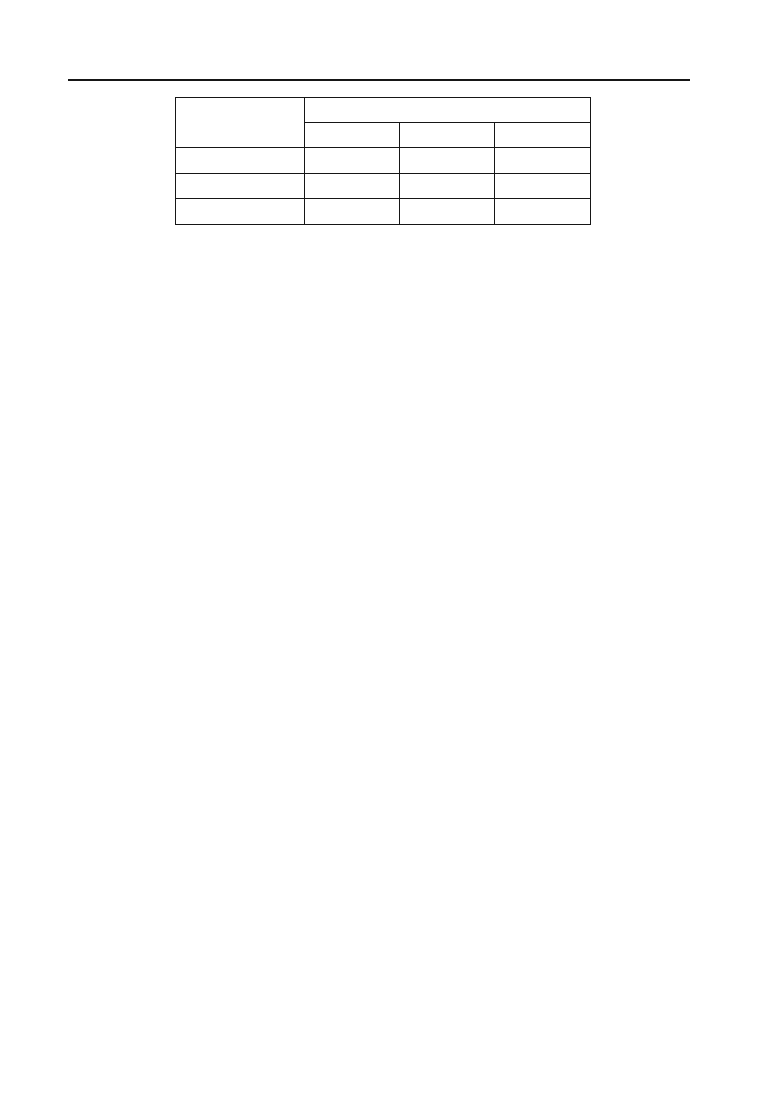
Приклад 1.110. З деякого листового матеріалу необхідно викрої+
ти 200 заготовок типу А, 260 — типу В і 290 — типу С.
70
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
При цьому можна застосувати три способи розкроювання.
Кількість заготовок, одержуваних з кожного листа при кожному спо+
собі розкроювання, наведена в наступній таблиці. Записати в матема+
тичній формі умови виконання завдання. Встановити, скільки листів
буде потрібно для викроювання означеної кількості заготовок.
Розв’язок. Позначимо через х
1
, х
2
, х
3
— кількість листів матеріалу,
що розкроєні відповідно першим, другим і третім способами. Тоді за
першим способом розкроювання х
1
листів буде отримано 3х
1
загото+
вок типу А, за другим — 2х
2
, за третім х
3
. Для повного виконання
завдання по заготовкам типу А сума 3х
1
+ 2х
2
+ х
3
повинна дорівню+
вати 200, тобто
3х
1
+ 2 х
2
+ х
3
= 200.
Аналогічно одержуємо рівняння:
х
1
+ 6х
2
+ 2х
3
= 260,
4х
1
+ х
2
+ 5х
3
= 290,
яким повинні задовольняти невідомі х
1
, х
2
, х
3
для того, щоб виконати
завдання по заготовкам В і С.
Система лінійних рівнянь
123
123
12 3
3 2 200,
6 2 260,
4 5 290.
xxx
xxx
xx x
°
®
°
¯
виражає в математичній формі умови виконання всього завдання по
заготовкам А, В, С.
Для розв’язку системи використаємо метод Гауса. Перепишемо
одержану систему у вигляді
123
123
12 3
6 2 260,
3 2 200,
4 5 290.
xxx
xxx
xx x
°
®
°
¯
Спосіб розкроювання Тип
заготовки
1 2 3
А 3 2 1
В 1 6 2
С 4 1 5
