Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


91
Розділ II. Аналітична геометрія
то умовою паралельності буде рівність
11
22
A
B
A
B
, а перпендикуляр+
ності є А
1
А
2
+ В
1
В
2
= 0.
Координати точки перетину двох прямих визначаються шляхом
розв’язання системи рівнянь цих прямих:
111
222
0
0
Ax By C
Ax By C
®
¯
x
x
'
'
,
y
y
'
'
, (2.14)
де
11
22
A
B
A
B
'
,
11
22
x
CB
CB
'
,
11
22
y
A
C
A
C
'
.
Відхиленням
G
заданої точки М
0
(х
0
; у
0
) від заданої прямої
Ах + Ву + С = 0 є довжина перпендикуляру, який опущено із цієї
точки на пряму, взята зі знаком плюс, якщо задана точка і початок
координат лежить по різні сторони від заданої прямої, і зі знаком
мінус, якщо вони лежать по одну сторону від прямої.
Відхилення
G
обчислюється за формулою:
00
22
A
xByC
A
B
G
r
.
Відстань d від точки М
0
(х
0
; у
0
) до прямої Ах + Ву + С = 0 є абсолют+
на величина відхилення точки М
0
(х
0
; у
0
) від прямої Ах + Ву + С = 0.
00
22
Ax By C
d
AB
. (2.15)
92
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.2.1. Приклади розв’язання задач
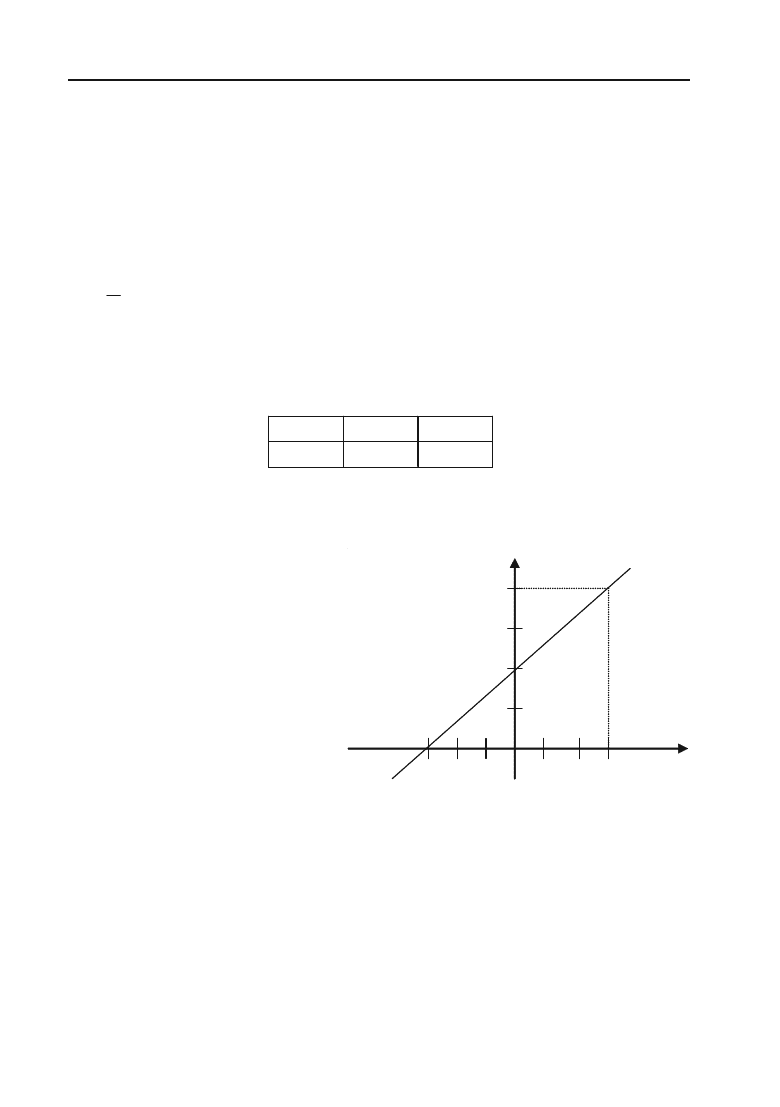
Задача 2.21. Побудувати пряму 2х – 3у + 6 = 0.
Загальний метод побудови прямої. Положення прямої на пло+
щині визначається двома точками, які належать цій прямій. Для
побудови прямої досить знати координати двох довільних точок цієї
прямої. Для цього обчислюємо значення у із даної рівності:
2
2
3
yx
при довільних значеннях х:
при значенні х = 0, у = 2;
при значенні х = 3, у = 4.
Складається наступна таблиця:
Таким чином, через одержані дві точки, координати яких В(0; 2)
та А(3; 4) будуємо пряму (рис. 2.6).
Другий спосіб. Оскільки
задана пряма містить вільний
член, то така пряма перети+
нає обидві координатні осі, а
так, як положення прямої
визначається координатами
двох точок, то достатньо зна+
ти точки перетину прямої з
координатними осями. Щоб
знайти точку перетину пря+
мої з віссю Оу, а задане рів+
няння підставимо х = 0 (будь+
яка точка, що лежить на осі
Оу, має абсцису, що дорівнює 0). Тоді –3у + 6 = 0, звідти у = 2.
Якщо покласти у = 0, отримаємо точку перетину прямої з віссю Ох:
2х + 6 = 0, х = –3. Позначимо одержані точки В(0; 2) і С(–3; 0).
Будуємо точки В і С та проводимо через них пряму (рис. 2.6).
Задача 2.22. Побудувати пряму 4х – у = 0.
Розв’язок. Так як вільний член рівняння дорівнює нулю, то пря+
ма проходить через початок координат. Якщо ми задамо довільне
х 0 3
у 2 4
Рис. 2.6.
Х
Y
С
В
А
О
93
Розділ II. Аналітична геометрія
значення х і знайдемо відповідне значення
у із заданого рівняння, то отримаємо ще
одну точку, яка лежить на прямій. Якщо
х = 1, то у = 4. Через точки О(0; 0) і М(1; 4)
проводимо пряму, рівняння якої 4х – у = 0
(рис. 2.7)
Задача 2.23. Побудувати прямі х + 4 =
0 і у – 3 = 0.
Розв’язок. 1) Розглянемо рівняння х + 4 = 0.
Запишемо його у вигляді х = –4. Це нам
говорить, що кожна точка прямої має по+
стійну абсцису, тобто пряма проходить
ліворуч від осі Оу на відстані 4 одиниці мас+
штабу від неї. Отже, пряма х + 4 = 0 пара+
лельна осі Оу і відтинає на осі Ох відрізок, рівний –4.
2) Аналогічно рівняння у – 3 = 0 показує, що всі точки цієї пря+
мої мають одну і ту ж ординату, тобто пряма у = 3 паралельна осі Ох
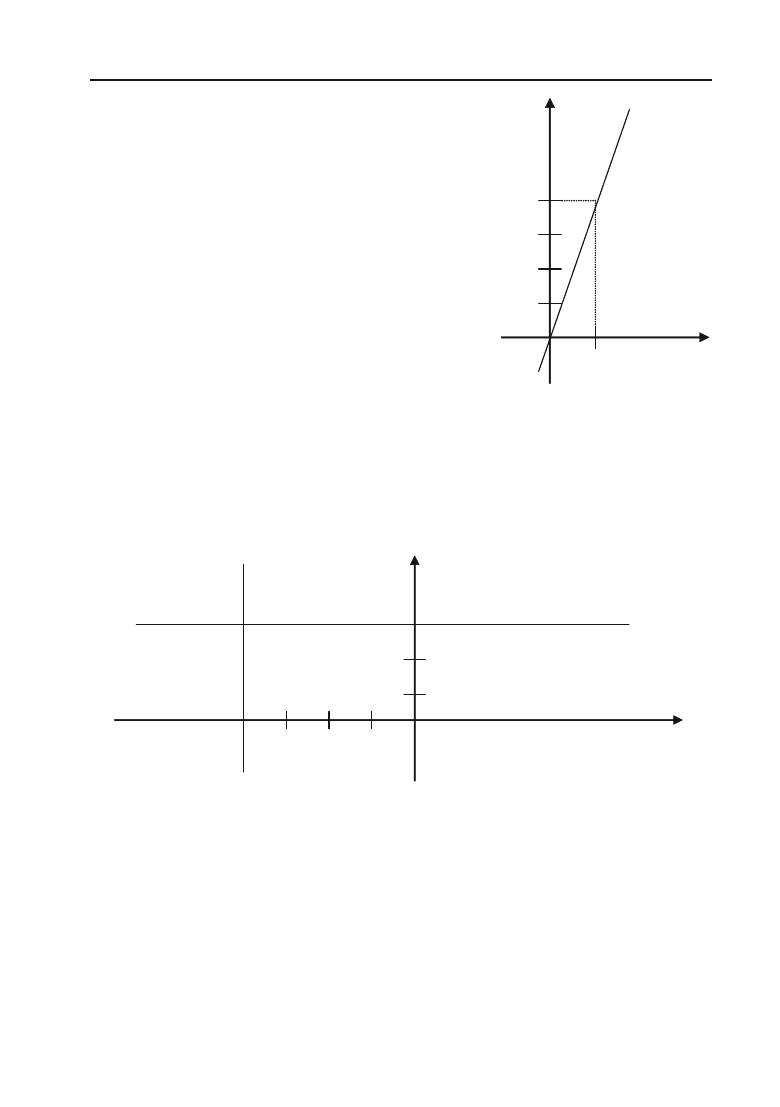
і відтинає на осі Оу відрізок, рівний 3 (одиниці масштабу) (рис. 2.8).
Рис. 2.8.
3 у – 3 = 0
–4
О
X
Y
x
+ 4 = 0
Рис. 2.7.
Х О
М
Y
Задача 2.24. Загальне рівняння прямої 3х – 4у + 12 = 0 предста+
вити у вигляді:
1) з кутовим коефіцієнтом;
2) у відрізках на осях;
3) побудувати пряму.
Розв’язок. 1) Рівняння (2.6) прямої з кутовим коефіцієнтом має
вигляд y = kx + b. Щоб задане рівняння перетворити до такого
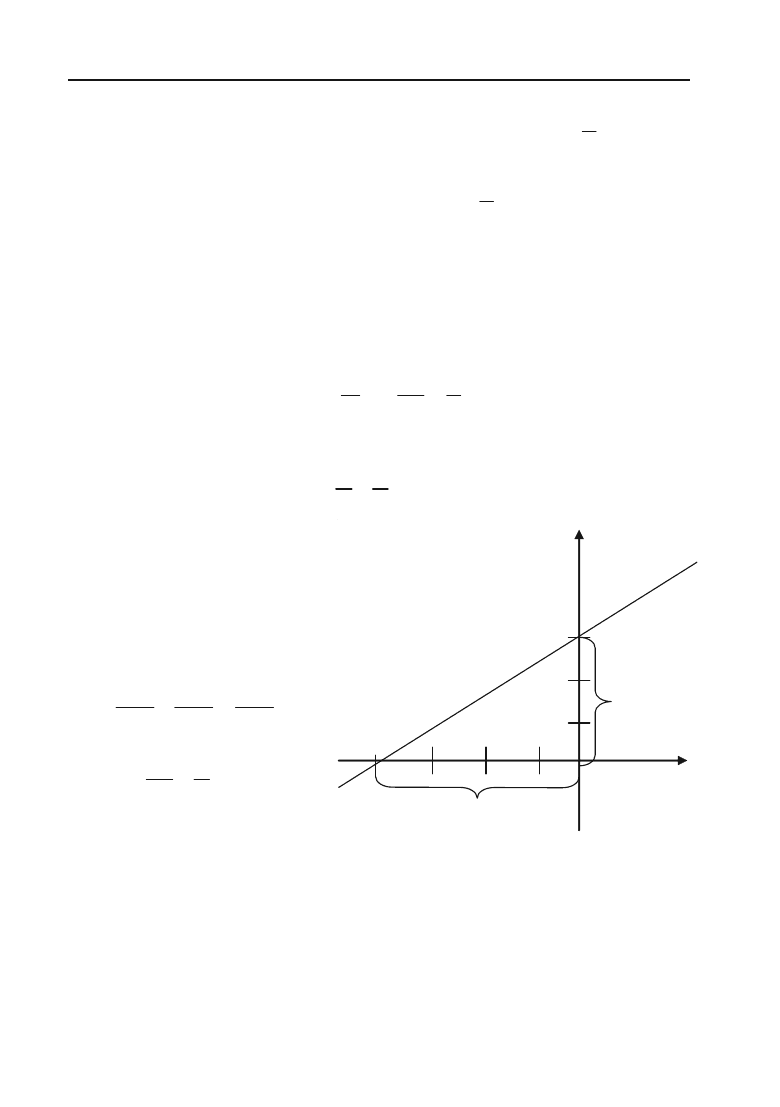
94
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
вигляду, розв’яжемо його відносно у: 4у = 3х + 12, у =
3
4
х + 3. Ба+
чимо, що тут кутовий коефіцієнт прямої
3
4
k
, а величина відрізка,
що відтинає пряма на осі ординат b = 3.
Необхідно запам’ятати, якщо рівняння прямої задано в загально+
му вигляді (2.6), то кутовий коефіцієнт цієї прямої легко одержати,
якщо розділити коефіцієнт при х на коефіцієнт при у і взяти одер+
жану частку з оберненим знаком:
33
44
A
k
B
.
2) У відрізках на осях рівняння прямої має вигляд (2.8)
1
xy
ab
.
Щоб одержати величини
відрізків, що відтинає пряма
на координатних осях, вико+
наємо перетворення:
3х – 4у + 12 = 0
3х – 4у = –12
34 12
12 12 12
xy
1
43
xy
.
3) Побудова: а = –4; b = 3
(рис. 2.9).
Задача 2.25. Скласти рівняння прямої, що відтинає на осі Оу
відрізок, рівний 4 (одиниць масштабу) та утворює з віссю Ох кут в 120
о
.
Розв’язок. Скористаємося рівнянням прямої з заданим кутовим
коефіцієнтом у = kx + b. Згідно умові
b = 4, k = tg 120
o
= tg (180
o
– 60
o
) = –tg 60
o
= –3, k = –3.
Рис. 2.9.
Х
Y
О
b = 3
a = –4
95
Розділ II. Аналітична геометрія
Шукане рівняння прямої буде:
у = –3х + 4 або 3х + у – 4 = 0.
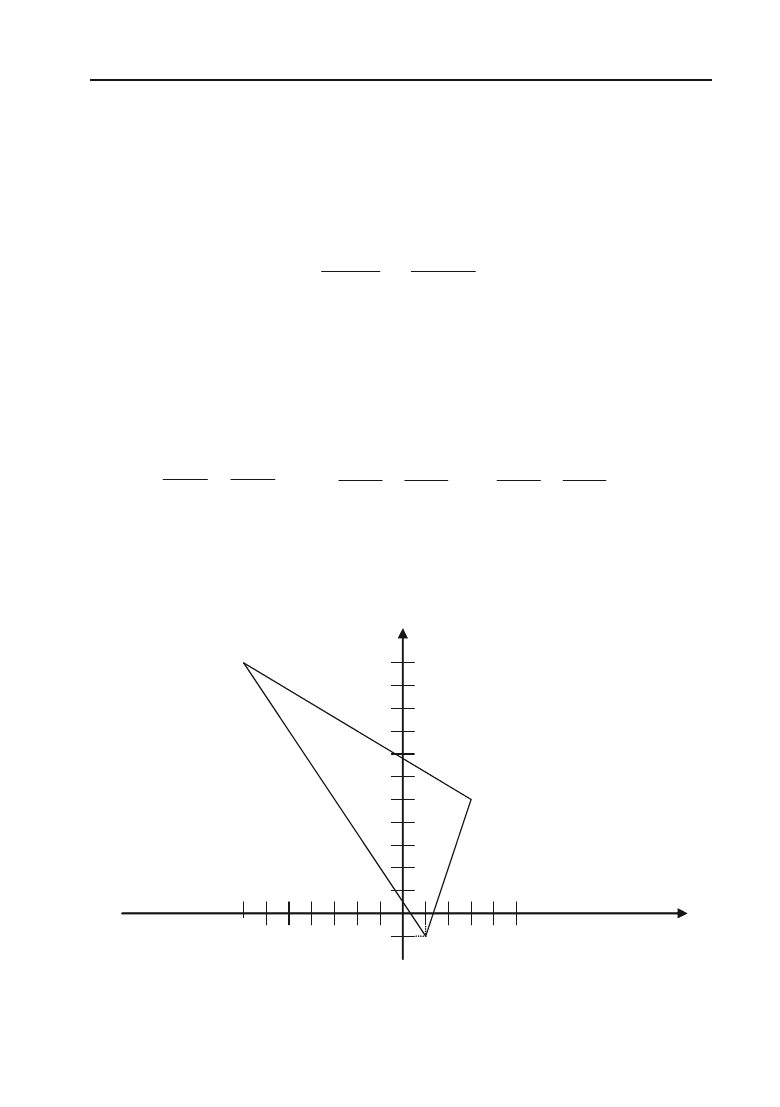
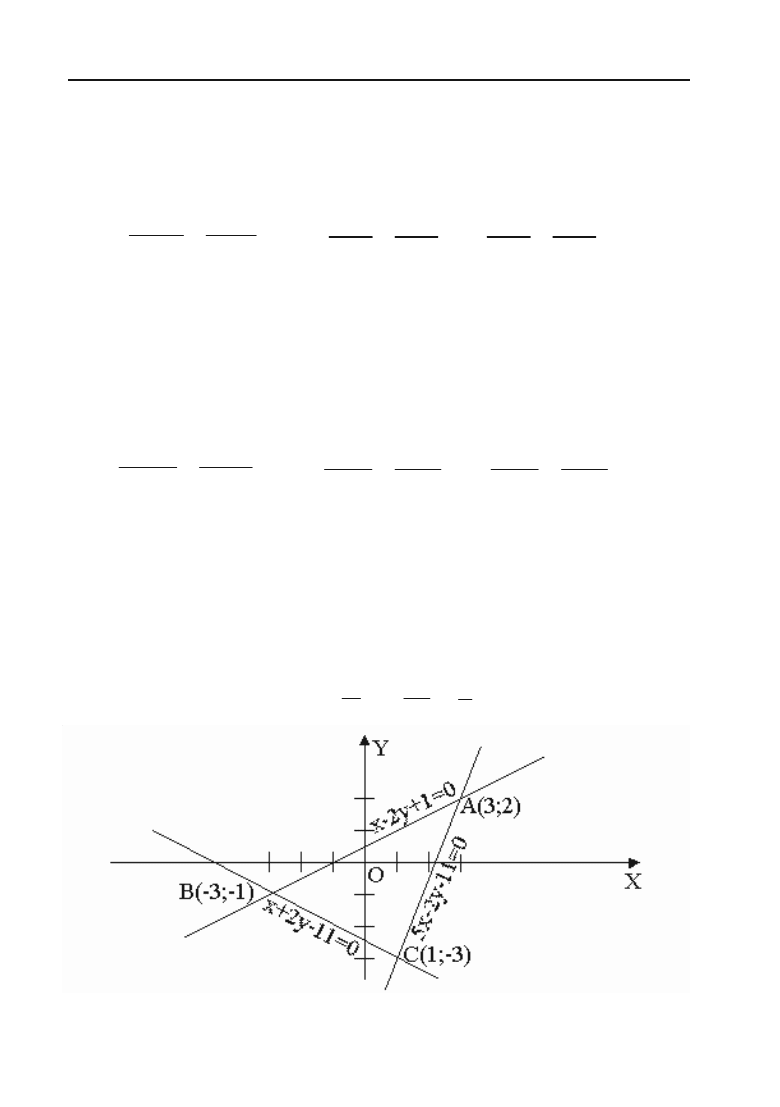
Задача 2.26. Знайти рівняння сторін трикутника, вершини яко+
го А(1; –1), В(3; 5), С(–7; 11).
Розв’язок. Скористаємося формулою (2.10):
11
221
1
x
xyy
x
xyy
.
Для знаходження рівняння сторони АВ беремо А(1; –1) та В(3; 5).
Нехай
х
1
= 1, у
1
= –1;
х
2
= 3, у
2
= 5;
Підставимо в рівняння (2.10):
11
31 51
xy
або
11 11
26 13
xy xy
3 (х – 1) = у + 1
3х – 3 = у + 1
3х – у – 4 = 0 (АВ).
Для знаходження рівняння сторони АС беремо А(1; –1) та
С(–7; 11).
Рис. 2.10.
–7
О
А(1;+1)
Х
Y
11
В(3; 5)
С(–7; 11)
96
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Нехай
х
1
= 1, у
1
= –1;
х
2
= –7, у
2
= 11.
Підставимо в рівняння (2.10):
11
71 111
xy
або
11 11
812 2 3
xy xy
3(х – 1) = –2(у + 1)
3х – 3 = –2у – 2
3х + 2у – 1 = 0 (АС).
Для знаходження рівняння сторони ВС беремо В(3; 5) та С(–7; 11).
Нехай
х
1
= 3, у
1
= 5;
х
2
= –7, у
2
= 11.
Підставимо в рівняння (2.10):
35
73 115
xy
або
35 35
10 6 5 3
xy xy
3(х – 3) = –5(у – 5)
3х – 9 = –5у + 25
3х + 5у – 34 = 0 (ВС).
Задача 2.27. Знайти кути та площу трикутника, сторони якого
задано рівняннями: 5х – 2у – 11 = 0; х + 2у + 5 = 0; х – 2у + 1 = 0.
Розв’язок. Побудуємо заданий трикутник.
Позначимо його вершини буквами А, В, С. Рівняння першої сто+
рони АВ є х – 2у + 1 = 0. Кутовий коефіцієнт прямої АВ
k
AB
=
A
B
=
1
2
=
1
2
.
Рис. 2.11.
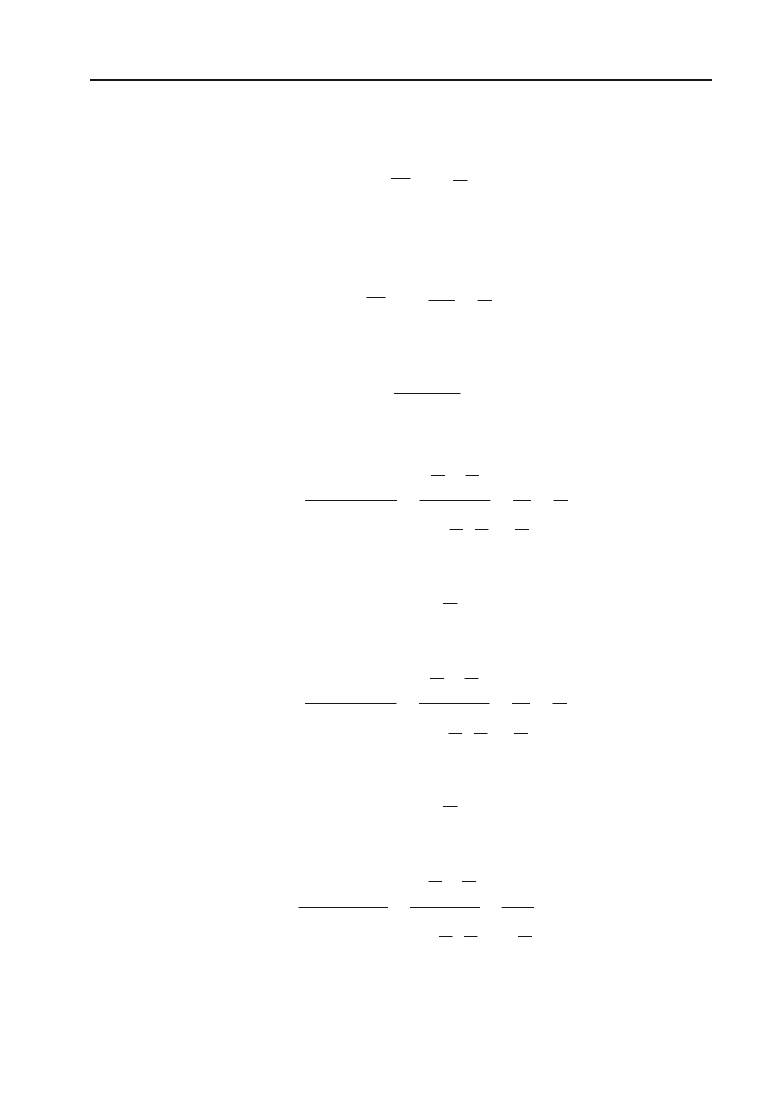
97
Розділ II. Аналітична геометрія
Рівняння прямої ВС є х + 2у + 5 = 0. Кутовий коефіцієнт пря+
мої ВС
k
ВС
=
A
B
=
1
2
.
Рівняння прямої АС є 5х – 2у – 1 = 0. Кутовий коефіцієнт пря+
мої АС
k
ВС
=
A
B
=
55
22
.
Кути трикутника будемо знаходити за формулою (2.11)
21
12
tg
1
kk
kk
M
,
51
28
22
tg
51 9
19
1
22 4
AC AB
AC AB
kk
A
kk
,
8
arct
g
9
A
.
11
14
22
tg
11 3
13
1
22 4
AB BC
AB BC
kk
B
kk
,
4
arct
g
3
B
.
15
3
22
tg 12
15 1
1
1
22 4
BC AC
CB AC
kk
C
kk
,
arct
g
12C
.

98
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Для того щоб знайти площу трикутника, необхідно визначити
координати його вершин. Точки А, В і С ми знайдемо, розв’язавши
системи рівнянь прямих, що дають ці прямі в перетині.
Розв’яжемо систему:
а)
52110
250
xy
xy
®
¯
Додамо до першого рівняння друге:
5х – 2у – 11 + х + 2у + 5 = 0 + 0;
6х – 6 = 0; 6х = 6; х = 1.
Підставимо отримане значення змінної х в будь+яке рівняння
системи, наприклад в друге:
1 + 2у + 5 = 0;
6 + 2у = 0; 2у = –6; у = –3.
Отримали точку С(1; –3).
б)
52110
210
xy
xy
®
¯
Віднімемо від першого рівняння друге:
5х – 2у – 11 – х – (–2у) – 1 = 0 – 0;
4х – 2у + 2у – 12 = 0; 4х = 12; х = 3.
Підставимо отримане значення змінної х у будь+яке рівняння,
наприклад у друге:
3 – 2у + 1 = 0;
4 – 2у = 0; 4 = 2у; у = 2.
Отримали точку А(3; 2).
в)
250
210
xy
xy
®
¯
Додамо до першого рівняння друге:
х + 2у + 5 + х – 2у + 1 = 0 + 0;
2х + 6 = 0; 2х = –6; х = –3.
Підставимо отримане значення змінної х у будь+яке рівняння,
наприклад у друге:
–3 –2у + 1 = 0; –2у = 2; у = –1.
Отримали точку В(–3; –1).

99
Розділ II. Аналітична геометрія
Знайдемо площину трикутника за формулою:
S =
1
2
(x
1
(y
2
– y
3
) + x
2
(y
3
– y
1
) + x
3
(y
1
– y
2
));
S =
1
2
(3(–1+3) – 3(–3 – 2) + 1(2 + 1)) =
1
2
(6 + 15 + 3) =
1
2
24 = 12.
Площа трикутника S = 12 кв. од.
Задача 2.28. Знайти рівняння прямої, що проходить через точку
М
0
(2; 5) паралельно прямій 3х – 4у + 15 = 0.
Розв’язок. Виходячи з того, що шукана пряма паралельна заданій,
її кутовий коефіцієнт дорівнює кутовому коефіцієнту заданої пря+
мої, тобто k
1
= k
2
= k.
k
1
=
33
44
A
B
= k
2
= k.
Складемо рівняння шуканої прямої за формулою:
у – у
0
= k(х – х
0
);
у – 5 =
3
4
(х – 2);
4у – 20 = 3х – 6;
3х – 4у + 14 = 0.
Шукане рівняння прямої 3х – 4у + 14 = 0.
Задача 2.29. Знайти рівняння прямої, що проходить через точку
Р
0
(5; –1) і перпендикулярна до прямої 3х – 7у + 14 = 0.
Розв’язок. Так як шукана пряма перпендикулярна заданій, то до+
буток кутових коефіцієнтів обох прямих має дорівнювати –1, тобто
k
1
k
2
= –1. Таким чином, кутовий коефіцієнт шуканої прямої має бути
обернений за абсолютною величиною і протилежний за знаком ку+
товому коефіцієнту заданої прямої:
2
1
1
k
k
.
Знайдемо кутовий коефіцієнт заданої прямої:
1
33
77
A
k
B
.

100
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
За умовою перпендикулярності:
2
1
1
k
k
=
17
3
3
7
.
Знаходимо рівняння шуканої прямої за формулою:
у – у
0
= k(х – х
0
),
у + 1 =
7
3
(х – 5),
3(у + 1) = –7(х – 5),
3у + 3 = –7х + 35,
7х + 3у – 32 = 0.
Шукане рівняння прямої: 7х + 3у – 32 = 0.
Задача 2.30. Знайти проекцію точки М(–8; 12) на пряму, що
проходить через точки С(2; –3) та D(–5; 1).
Розв’язок. Рівняння прямої СD знайдемо за формулою (2.10):
11
221
1
xx
yy
xx
yy
,
23
52 13
xy
,
4(х – 2) = –7(у + 3),
4х – 8 = –7у – 21,
4х + 7y + 13 = 0.
Проекцією точки М на пряму СD буде основа перпендикуляра,
який опущений із точки М на пряму СD. Рівняння перпендикуляра
MN можна знайти за формулою у – у
0
= k(х – х
0
), так як координати
точки М задано, а кутовий коефіцієнт, згідно умові перпендикуляр+
ності дорівнює:
2
1
1
k
k
=
17
4
4
7
;
у – 12 =
7
4
(х + 8);
