Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

121
Розділ II. Аналітична геометрія
2
3
3
x
§·
¨¸
¨¸
©¹
= 2рх;
2
3
x
= 2рх; х
2
= 6рх; х = 6р.
Тоді
6
43
cos30
3
2
o
OD p
OA p
.
Довжина сторін трикутника
43ap
.
2.3.6. Задачі для самостійного розв’язку
2.61. Скласти рівняння кола, що проходить через точку М(2; 6) і
його центр співпадає з точкою С(–1; 2).
2.62. Скласти рівняння кола, якщо мочки А(3; 2) і В(–1; 6) явля+
ються кінцями одного із діаметрів кола.
2.63. Скласти рівняння кола, центр якого співпадає з точкою
С(1; –1) і пряма 5х – 12у + 9 = 0 являється дотичною до кола.
2.64. Скласти рівняння кола, що проходить через точки А(3; 1) і
В(–1; 3), а його центр лежить на прямій 3х – у – 2 = 0.
2.65. Скласти рівняння кола, що проходить через точки А(1; 1),
В(1; –1) і С(2; 0).
2.66. Скласти рівняння еліпса, фокуси якого розміщені на осі
абсцис симетрично відносно початку координат. Знаючи, що:
1) його велика вісь дорівнює 10, а відстань між фокусами 2с = 8;
2) його мала вісь дорівнює 24, а відстань між фокусами 2с = 10;
3) відстань між його фокусами 2с = 6 і ексцентриситет
3
5
e
;
4) його велика вісь дорівнює 20, а ексцентриситет
3
5
e
;
5) його мала вісь дорівнює 10, а ексцентриситет
12
13
e
.

122
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.67. Скласти рівняння еліпса, фокуси якого розміщені на осі
абсцис симетрично відносно початку координат, якщо задано:
1) точка М
1
(
25
; 2) і його мала піввісь b = 3;
2) точка М
1
(2; –2) і його велика піввісь а = 4;
3) точки М
1
(4;
3
) і М
2
(
22
; 3) еліпса;
4) точка М
1
(
15
; –1) еліпса і відстань між його фокусами 2с = 8;
5) точка М
1
(2;
5
3
) еліпса і його ексцентриситет
2
3
e
.
2.68. Знайти ексцентриситет еліпса, знаючи, що:
1) малу вісь його видно із фокуса під прямим кутом;
2) відстань між фокусами дорівнює відстані між вершинами малої
та великої осей.
2.69. Скласти рівняння гіперболи, фокуси якої розміщені на осі
абсцис симетрично відносно початку координат, знаючи, що:
1) відстань між фокусами 2с = 10 і вісь 2b = 8;
2) відстань між фокусами 2с = 6 і ексцентриситет
3
2
e
;
3) вісь 2а = 16 і ексцентриситет
5
4
e
;
4) рівняння асимптот
4
3
y
x r
і відстань між фокусами 2с = 20;
5) точки М
1
(6; –1) і М
2
(–8;
22
) знаходяться на гіперболі;
6) точка М
1
(–5; 3) гіперболи і ексцентриситет
2e
;
7) точка М
1
(
9
2
; –1) гіперболи та рівняння асимптот
2
3
y
x r
.
2.70. Знайти ексцентриситет гіперболи при умові, що
1) кут між асимптотами дорівнює 60
о
;
2) кут між асимптотами дорівнює 90
о
.
2.71. Побудувати параболи, що задані рівняннями:
1) у
2
= 6х;

123
Розділ II. Аналітична геометрія
2) у
2
= –6х;
3) х
2
= 6у;
4) х
2
= –6у;
а також їх фокуси та директриси. Написати рівняння директрис.
2.72. Скласти рівняння параболи, вершина якої знаходиться в
початку координат. Знаючи, що:
1) парабола розміщена симетрично відносно осі Ох і проходить
через точку М(9; 6);
2) парабола розміщена симетрично відносно осі Ох і проходить
через точку Р(–1; 3);
3) парабола розміщена симетрично відносно осі Оу і проходить
через мочку Q(1; 1);
4) парабола розміщена симетрично відносно осі Оу і проходить
через мочку R(4; –8).
2.73. Скласти рівняння параболи і її директриси, якщо парабола
проходить через точки перетину прямої х + у = 0 і кола х
2
+ у
2
– 4х = 0
і симетрична відносно осі Оу.
2.74. Відстань між двома торговими організаціями дорівнює 8 км.
Знайти рівняння множини всіх можливих місцезнаходжень баз, які
обслуговують ці організації, якщо відомо, що сума відстаней від бази
до них повинна бути постійною та дорівнювати 20 км.
2.75. Відстань між двома заводами, що виробляють однакову
продукцію, дорівнює 400 км. Транспортні витрати на перевезення
продукції від заводу А складають 2 грош. од. за 10 км, а від заводу
В — 3 грош. од. за 10 км. Визначити межу районів, для яких однако+
во вигідно придбання продукції та підприємстві А, так і на підпри+
ємстві В.

124
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§ 2.4. Задачі економічного змісту
Розглянемо деякі приклади застосування лінійної залежності в
економіці.
1. Якщо через k позначити тариф перевезення вантажу на одини+
цю відстані, b – витрати при перевезенні вантажу, що не залежать
від відстані х, то загальну вартість у перевезення вантажу на відстань
х можна обчислити за допомогою формули у = kx + b.
2. Якщо позначити через у витрати підприємства в продовж міся+
ця при випуску х одиниць однорідної продукції, то у може бути
визначено за формулою у = kx + b, де величина kх буде визначати
змінні витрати, що залежать від обсягу випуску (де k — витрати
підприємства впродовж місяця на одиницю продукції). Величина b
визначає постійні витрати підприємства, які не залежать від обсягу
продукції, що випускається (витрати за рахунок амортизації будин+
ку, заробітної платні охорони, службовців і допоміжних робітників,
опалення будинку і т.п.).
2.4.1. Приклади розв’язання задач
Задача 2.76. Валова продукція на 1 га сільськогосподарських
угідь за чотири роки збільшилась на 24%. Скласти рівняння прямої,
яка відображує зміну валової продукції на 1 га протягом чотирьох
років за умови, що валова продукція у відсотках змінюється пропор+
ційно часу. Дослідити вплив розширення тракторного парку на зро+
стання врожаю зернових.
Розв’язок. Валову продукцію, випущену у перший рік, приймає+
мо за 100% і будемо шукати рівняння прямої у вигляді у = kx + b:
k =
24
4
= 6,1; 100 = 6,1
1 + b; b = 93,9.
Отже у = 6,1х + 93,9, де х — рік.
Задача 2.77. В 1980 р. держава мала 108,5 тисяч тракторів і одер+
жала з одного гектара 8,5 ц зернових. В 1995 р. держава мала 510
тисяч тракторів і одержала з одного гектара 21 ц зернових.
Розв’язок. Позначимо час — x, кількість тисяч тракторів — y; вро+
жай, який одержали з одного гектара, позначимо — z (центнерів).
125
Розділ II. Аналітична геометрія
За умовою задачі маємо чотири точки:
A(х
1
, у
1
); х
1
= 1980, y
1
= 108,5;
B(х
2
, у
2
); х
2
= 1995, y
2
= 510;
M(х
1
, z
1
); х
1
= 1980, z
1
= 8,5;
M(х
2
, z
2
); х
2
= 1995, z
2
= 21.
Знайдемо рівняння прямих — графіків зростання тракторного
парку та врожайності зернових з одного гектара за 1980–1995 роки у
вигляді y = kx + b, — рівняння прямої з кутовим коефіцієнтом.
Використовуючи рівняння прямої, що проходить через дві задані
очки, одержимо:
1980 108.5 1980 108,5
1995 1980 510 108.5 15 401,5
xyxy
401,5 401,5 1980 15 15 108,5
xy
15 15 108,5 401,5 401,5 1980
y
x
401,5 793342,5
15 401,5 793342,5
15 15
yx y x
.
Таким чином, кутовий коефіцієнт прямої зростання тракторного
парку буде:
1
401.5
26,77
15
k |
.
Використовуючи точки M
1
та M
2
, аналогічно знаходимо рівняння
прямої зростання врожайності зернових з одного гектара.
1980 8,5 1980 8,5
1995 1980 21 8,5 15 12,5
xzxz
12,5 1980 12,5 15 8,5 15
x
z
15 12,5 12,5 1980 8,5 15
z
x
15 12,5 24877,5
z
x
.
Отже її кутовий коефіцієнт буде:
2
12,5
0,83
15
k |
.
126
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
З умов задачі можна зробити висновок, що при зростанні трак+
торного парку врожайність зернових з 1га зростає. Але кутовий ко+
ефіцієнт k
1
графіка зростання кількості тракторів значно більший за
кутовий коефіцієнт k
2
графіка зростання врожайності зернових. Та+
ким чином, зростання тракторного парка сприяє зростанню врожай+
ності. Зернових, але не пропорційно. Зростання кількості тракторів —
зростання енергоозброєності сільського господарства не є основним
фактором у підвищенні ефективності сільського господарства. Необ+
хідно враховувати вплив інших факторів, наприклад, якості насіння,
культуру агротехніки.
Задача 2.78. Транспортні витрати перевезення одиниці вантажу
(y) залізничним та автомобільним транспортом на відстань (x) зна+
ходять за формулами:
1
10
2
yx
та
5
y
x
,
де (x) вимірюється десятками км. Визначити рентабельність транс+
портного постачання.
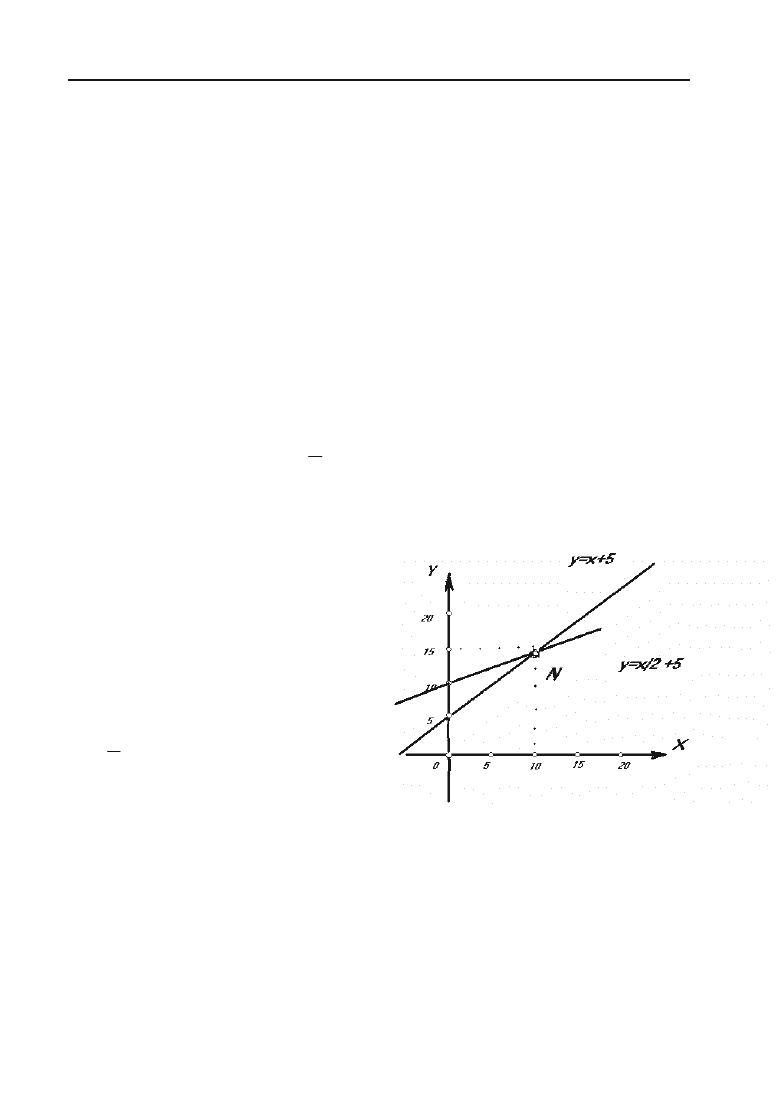
Розв’язок. Побудуємо графіки
транспортних витрат перевезення
(див. рис. 2.19). Графіки прямих
перетинаються в точці N(10; 15).
Для перевірки координат точки N
знайдемо точку перетинає аналі+
тично:
1
10
2
5
xy
xy
°
®
°
¯
220
5
xy
xy
®
¯
15; 10yx
.
Графіки витрат дозволяють зробити висновок:
а) коли x
[0, 10], тобто x < 100 км, транспортні витрати у пере+
везення автотранспортом нижче витрат перевезення залізничним
транспортом;
б) коли x
[10,
f
], тобто x > 100 км, більш рентабельним буде
залізничний транспорт.
Рис. 2.19.
127
Розділ II. Аналітична геометрія
Наведемо приклади задач, пов’язані з використанням рівнянь
другого порядку.
Задача 2.79. Дослідженням виявлено, що витрати палива суд+
ном на підводних крилах зростають пропорційно квадрату швидкості
судна. Треба знайти аналітичну залежність між витратами палива m
та швидкістю судна V, враховуючи, що при V = 40 км/год витрачено
20 л палива за годину, а також визначити витрати палива за годину
при швидкості 60 км/год.
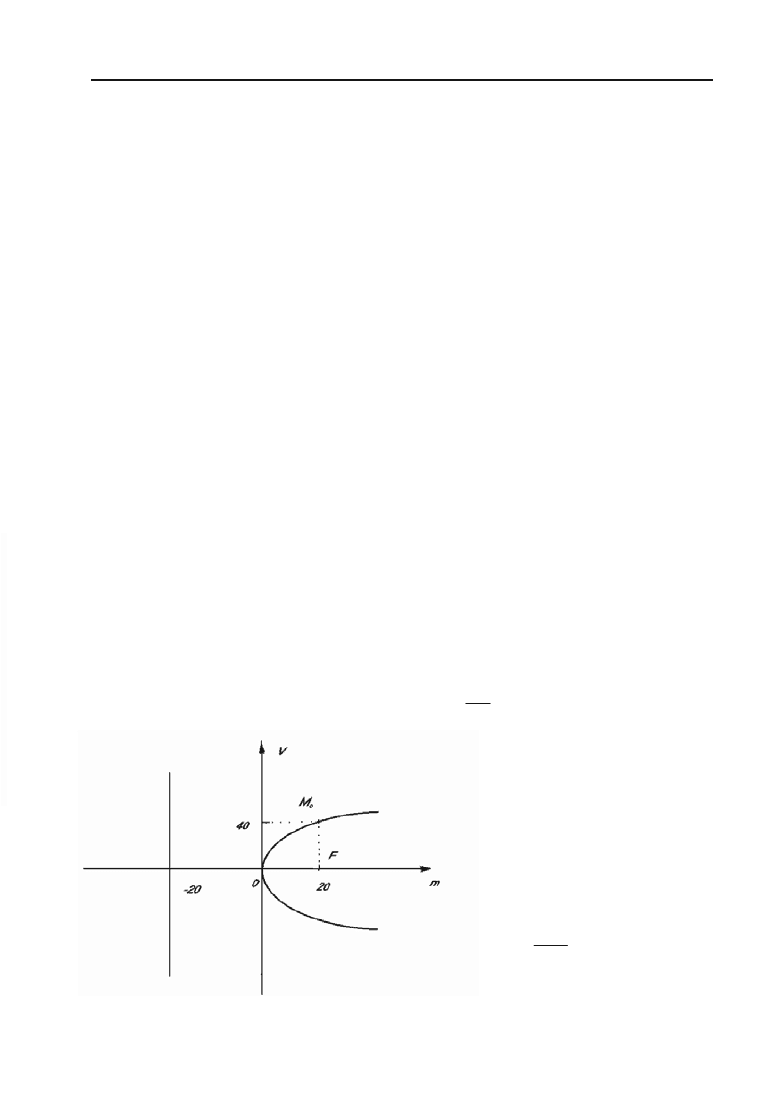
Розв’язок. Згідно з умовою задачі шукану залежність записати у
вигляді:
2
vkm
,
де k — деякий коефіцієнт пропорційності
Порівняння цієї формули з рівнянням параболи
2
2
y
px
доз+
воляє зробити висновок, що витрати палива змінюються за парабо+
лічним законом. При m = 0 швидкість V = 0, тобто парабола прохо+
дить через початок системи координат mОV. Згідно з умовою задачі
парабола проходить через точку M
0
(20; 40), тому її координати задо+
вольняють рівнянню параболи
40
2
= k
20, k = 80.
Таким чином, аналітична залежність між витратами палива та
швидкістю судна буде:
2
2
80
80
v
vmm
.
Графік цієї залеж+
ності зображено на рис.
2.20. З останньої формули
випливає, що при швид+
кості 60 км/год витрати
палива (у літрах) за годи+
ну повинні дорівнювати:
2
60
45
()
80
mлітрів
.
Рис. 2.20.
128
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Задача 2.80. Два однотипних підприємства А та В виробляють
продукцію з однією і тією ж відпускною оптовою ціною т за один
виріб. Однак автопарк, що обслуговує підприємство А, оснащений
новішими та потужнішими вантажними автомобілями. Тому транс+
портні витрати на перевезення одного виробу складають за 1 км: для
підприємства А — 10 грош. од., а для підприємства В — 20 грош. од.
Відстань між підприємствами 300 км. Як територіально має бути
поділений ринок збуту між двома підприємствами для того, щоб
витрати споживача на відвантаження виробів та їх транспортування
були мінімальними?
Рішення. Позначимо через S
1
та S
2
відстані до ринку від пунктів А
та В відповідно. Тоді витрати споживачів складуть:
f(A) = m + 10S
1
;
f(B) = m + 20S
2
.
Знайдемо множину точок, для яких S
1
= 2S
2
, тобто ті випадки
розміщення ринку, коли f(A) = f(B).
S
1
=
22
xy
; S
2
=
22
(300 )xy
.
22
xy
=
22
2 (300 )xy
;
x
2
+ y
2
= 360000 – 2400x + 4x
2
+ 4y
2
;
(x – 400)
2
+ y
2
= 200
2
.
Це коло. Таким чином, для споживача всередині кола вигідніше
купувати у пункті В, поза колом — у пункті А, а на колі — однаково.
Задача 2.81. Компанія виробляє вироби A та продає їх по 2 до+
лари за кожний. Керівництво компанії встановило, що сума у
В
за+
гальних щотижневих витрат (в доларах) на виготовлення виробів А
кількістю x (тисяч одиниць) має таку закономірність:
2
1000 1300 100
B
y
xx
.
Визначити щотижневу кількість виготовлення та продажу виробів
А, яка забезпечує рівновагу витрат та доходу.
Розв’язання. Доход від продажу x тисяч виробів A вартістю 2
долари за кожний буде:
2000
Д
y
x
.
Для рівноваги доходу та витрат треба щоб виконувалась рівність:

129
Розділ II. Аналітична геометрія
22
12
1000 1300 100 2000 7 10 0
(2)(5)0 2; 5.
ВД
уу x x xx x
xx x x
Отже, ця задача має дві точки рівноваги. Компанія може вироб+
ляти 2000
(x – 2) виробів A з доходом та витратами 4000 доларів,
або 5000 (х = 5) виробів з доходом та витратами 10000 доларів.
Розглянемо на цьому прикладі можливості компанії. Позначимо
щотижневий прибуток Р, тоді
2
2
2000 (1000 1300 100 )
1000 700 100 100( 2)( 5).
ДВ
PY Y x x x
xx xx
З останньої рівності випливає, що при x = 2 або x = 5 маємо Р = 0,
тобто ці значення х будуть точками рівноваги.
Коли 2 < x < 5, тоді х – 2 > 0, x – 5 < 0 і маємо Р > 0. Тобто
компанія одержить прибуток. При інших значеннях х, тобто коли
х
[2, 5] будемо мати Р < 0 — компанія несе збитки.
2.4.2. Задачі для самостійного розв’язку
2.82. Витрати виробника на 10 одиниць деякого товару склада+
ють 1000 грошових одиниць, 50 одиниць товару — 2000 грошових
одиниць. Визначити витрати виробництва на 30 одиниць за умови,
що витрати залежать від обсягу лінійно.
2.83. Скласти рівняння прямої, яка відображує зміну врожайності
1 га протягом 17 років, якщо у перший рік з 1 га було зібрано 9,1 ц
зернових культур, а в останній рік — 21 ц.
2.84. Припускається, що перенесення вартості машини на про+
дукцію, що виготовляється за її допомогою залежить від часу t. Не+
хай первісна вартість у = 25000 грошових одиниць, а термін служби
машини — 10 років. Побудувати лінію залежності перенесеної на
продукцію частини вартості машини від терміну її служби. Якою буде
ця величина через 8 років.
2.85. Витрати на перевезення двома видами транспорту відобра+
жаються функціями у = 50х + 150, у = 25х + 250, де х — відстань
перевезень, км, а у — транспортні витрати, грош. од. При яких відста+
нях економічніше користуватися першим видом транспорту?

130
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.86. Перевезення вантажу від даного міста до першого пункту,
який знаходиться на відстані 100 км, коштує 200 грош. од., а до дру+
гого, що знаходиться на відстані 400 км — 350 грош. од. Встановити
залежність вартості перевезення у від відстані х, якщо вартість є
лінійною функцією від відстані (якість доріг не враховується).
2.87. Два підприємства, що віддалені одне від одного на 100 км,
виробляють деякі одинакові вироби. Ціна реалізації одиниці виробу
для обох підприємств однакова і дорівнює m. Нехай транспортні
витрати на перевезення одиниці виробу від підприємства А до спо+
живача складають 1 грош. од. на 1 км, а від В — 2 грош. од. на 1 км.
Для яких споживачів витрати на придбання одиниці виробу в
підприємстві А і В повинні бути однаковими? Як доцільно прикріпи+
ти споживачів до підприємств?
2.88. Розв’язати задачу 2.87 за умови, що транспортні витрати на
1 км шляху при перевезенні одного виробу від підприємства А та В
до споживача однакові і складають 1 грош. од. на 1 км, а ціна реалі+
зації кожного виробу на підприємствах А і В дорівнює 200 і 225 грош.
од. відповідно.
2.89. Розв’язати задачу 2.87 за умови, що транспортні витрати на
1 км шляху при перевезенні одного виробу від підприємства А скла+
дають 9 грош. од. на 1 км, а від підприємства В — 3 грош. од. на 1 км.
2.90. Відстань між двома заводами, що виробляють однакову
продукцію, дорівнює 300 км. Транспортні витрати на транспортуван+
ня продукції від заводу А вдвічі більші ніж від В. Визначити лінію —
межу районів, на якій однаково вигідно одержувати продукцію від
заводів А та В.
