Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


131
Розділ II. Аналітична геометрія
§ 2.5. Площина та пряма в просторі
2.5.1. Площина
Будь+яке рівняння першого степеня з трьома змінними визначає
площину. І навпаки, будь+яка площина визначається рівнянням пер+
шого степеня відносно змінних координат, які задають довільну точ+
ку площини.
2.5.1.1. Загальне рівняння площини
Загальне рівняння площини має вигляд:
Ax + By + Cz + D = 0, (2.21)
де числа А, В, С — координати нормального вектора.
Особливі випадки рівняння (2.21):
а) Якщо в рівняння (2.21) вільний член D = 0, тоді одержуємо
рівняння
Ax + By + Cz = 0 (2.22)
площини, що проходить через початок координат.
б) Нехай в рівняння (2.21) один із коефіцієнтів А, В або С дорів+
нює нулю. Тоді одержимо рівняння площин, які паралельні відповід+
ним координатним осям.
Рівняння площини, що паралельна осі Ох:
By + Cz + D = 0. (2.23)
Рівняння площини, що паралельна осі Оу:
Ax + Cz + D = 0. (2.24)
Рівняння площини, що паралельна осі Оz:
Ax + By + D = 0. (2.25)
Необхідно запам’ятати, що якщо площина паралельна якій+небудь
координатній осі, то в її рівняння відсутній член, який містить коор+
динату, однойменну з цією віссю.
в) Якщо в рівняннях (2.23), (2.24), (2.25) вільний член D = 0, то
одержимо рівняння площин, які проходять через відповідні осі ко+
ординат.
Рівняння площини, що проходить через вісь Ох:
By + Cz = 0.

132
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Рівняння площини, що проходить через вісь Оу:
Ax + Cz = 0.
Рівняння площини, що проходить через вісь Оz:
Ax + By = 0.
г) Нехай в рівнянні (2.21) два коефіцієнта дорівнюють нулю, тоб+
то: В = С = 0, або А = С = 0, або А = В = 0. Тоді одержуємо рівняння
площин, які паралельні відповідним координатним площинам:
Рівняння площини, що паралельна координатній площині yOz:
Ax + D = 0, або х = а.
Рівняння площини, що паралельна координатній площині хOz:
By + D = 0, або у = b.
Рівняння площини, що паралельна координатній площині хOу:
Cz + D = 0, або z = с.
д) Нехай в рівнянні (2.21) три коефіцієнти B, C i D, або A, C i D,
або A, B i D дорівнюють нулю. Тоді одержуємо рівняння координат+
них площин.
Рівняння координатної площини yOz:
Ах = 0, або х = 0.
Рівняння координатної площини хOz:
Ву = 0, або у = 0.
Рівняння координатної площини хOу:
Сz = 0, або z = 0.
2.5.1.2. Рівняння площини в відрізках
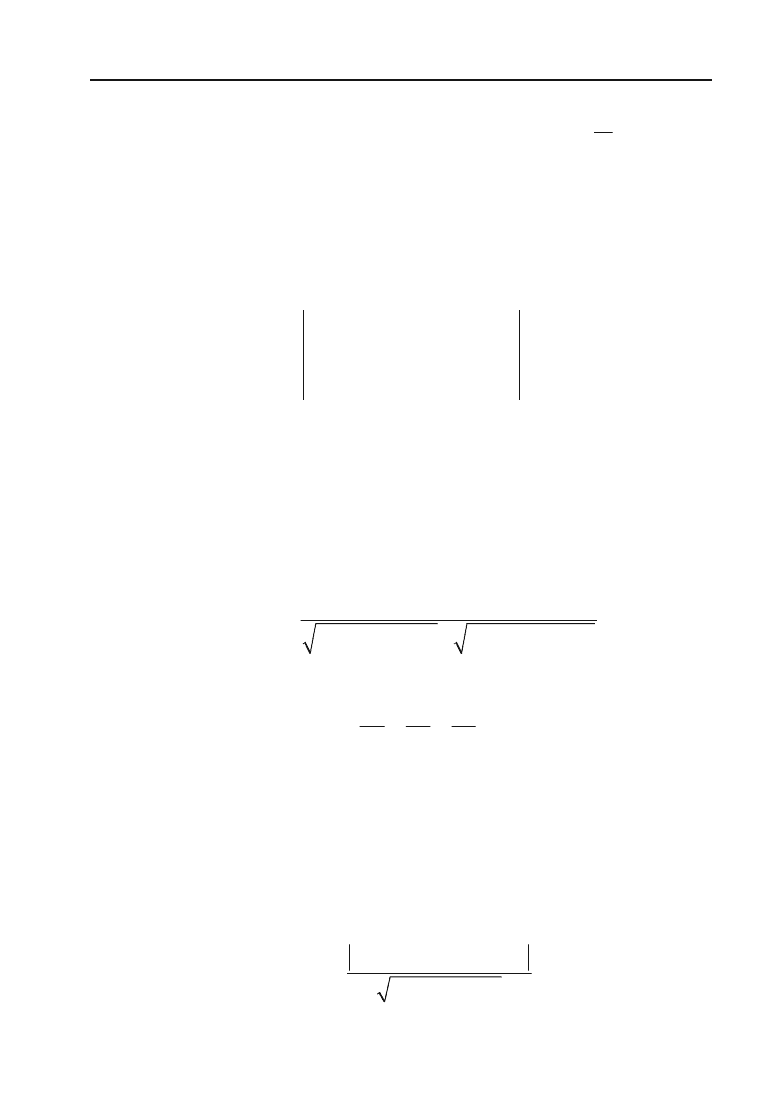
Рівняння площини в відрізках має вигляд:
1
xyz
abc
, (2.26)
де а, b і с — величини відрізків, які відтинає площина на осях координат.
2.5.1.3. Рівняння площини, що проходить через задану точку
Рівняння площини, що проходить через задану точку М
0
(х
0
; у
0
; z
0
)
має вигляд:
133
Розділ II. Аналітична геометрія
А(х – х
0
) + В(у – у
0
) + С(z – z
0
) = 0, (2.27)
де А, В, С — координати нормального вектора площини
N
= {А; В; С}.
2.5.1.4. Рівняння площини, що проходить через три задані точки
Рівняння площини, що проходить через три задані точки
М
1
(х
1
; у
1
; z
1
), М
2
(х
2
; у
2
; z
2
) і М
3
(х
3
; у
3
; z
3
), які не лежать на одній прямій
має вигляд:
111
212121
313131
0
xx yy zz
xxyyzz
xxyyzz
. (2.28)
2.5.1.5. Кут між двома площинами
Кут між двома площинами, які задані рівняннями:
A
1
x + B
1
y + C
1
z + D
1
= 0,
A
2
x + B
2
y + C
2
z + D
2
= 0
визначається за формулою:
12 12 12
22 22 2
111 222
cos
*
AA BB CC
ABC ABC
M
r
. (2.29)
Умова паралельності двох площин має вигляд:
111
222
ABC
ABC
. (2.30)
Умова перпендикулярності двох площин має вигляд:
А
1
А
2
+ В
1
В
2
+ С
1
С
2
= 0. (2.31)
2.5.1.5. Відстань між точкою та площиною
Відстань від точки М
0
(х
0
; у
0
; z
0
) до площини Ax + By + Cz + D = 0
визначається за формулою:
000
222
Ax By Cz D
d
ABC
. (2.32)

134
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.5.2. Пряма лінія в просторі
2.5.2.1. Загальне рівняння прямої
Пряма лінія в просторі визначається як лінія перетину двох пло+
щин. В такому випадку вона визначається системою двох рівнянь
першого ступеню:
1111
2222
0
0
Ax By Cz D
Ax By Cz D
®
¯
(2.33)
Рівняння (2.33), які розглядаються сумісно, називаються
загаль,
ними рівняннями прямої в просторі.
2.5.2.2. Канонічне рівняння прямої в просторі
Канонічне рівняння прямої в просторі має вигляд:
111
xx
yy
zz
lmn
,
де х
1
, у
1
, z
1
— координати заданої точки М
1
, що лежить на прямій; х,
у, z — поточні координати довільної точки прямої; l, m, n — напрямні
коефіцієнти, які пропорційні напрямним косинусами прямої.
Від загальних рівнянь прямої (2.33) можна перейти до її каноніч+
ного рівняння (2.34). Для цього необхідно:
а) Знайти яку+небудь її точку М
1
(х
1
; у
1
; z
1
). Потрібно задати чис+
лове значення однієї з невідомих координат х або у, або z, і підстави+
ти його замість відповідної координати в загальні рівняння прямої.
Одержимо систему двох рівнянь з двома невідомими. Розв’язавши
цю систему, визначимо дві інші координати.
б) Знайти направляючий вектор
S
= {l; m; n} прямої. За вектор
S
беремо вектор, перпендикулярний до векторів
1
N
= {A
1
; B
1
; C
1
} i
2
N
= {A
2
; B
2
; C
2
}, тобто векторний добуток
12
SNN u
,
або
11 11 11
22 22 22
BC C A AB
Sijk
BC C A AB
.

135
Розділ II. Аналітична геометрія
Отже,
11 11 11
22 22 22
, ,
BC C A AB
lmn
BC C A AB
.
2.5.2.3. Векторне рівняння прямої
Векторне рівняння прямої має вигляд:
1
rrSt
,
де
r
— радіус+вектор довільної точки М;
1
r
— радіус+вектор заданої точки М
1
;
S
= {l; m; n} — напрямний вектор, що паралельний заданій прямій;
t — змінний параметр.
2.5.2.4. Параметричні рівняння прямої
1
1
1
;
;
,
x
lt x
y
mt y
z
nt z
°
®
°
¯
де х
1
, у
1
, z
1
— координати точки М
1
, що лежить на прямій;
х, у, z — координати довільної точки прямої;
l, m, n — напрямні коефіцієнти;
t — змінний параметр.
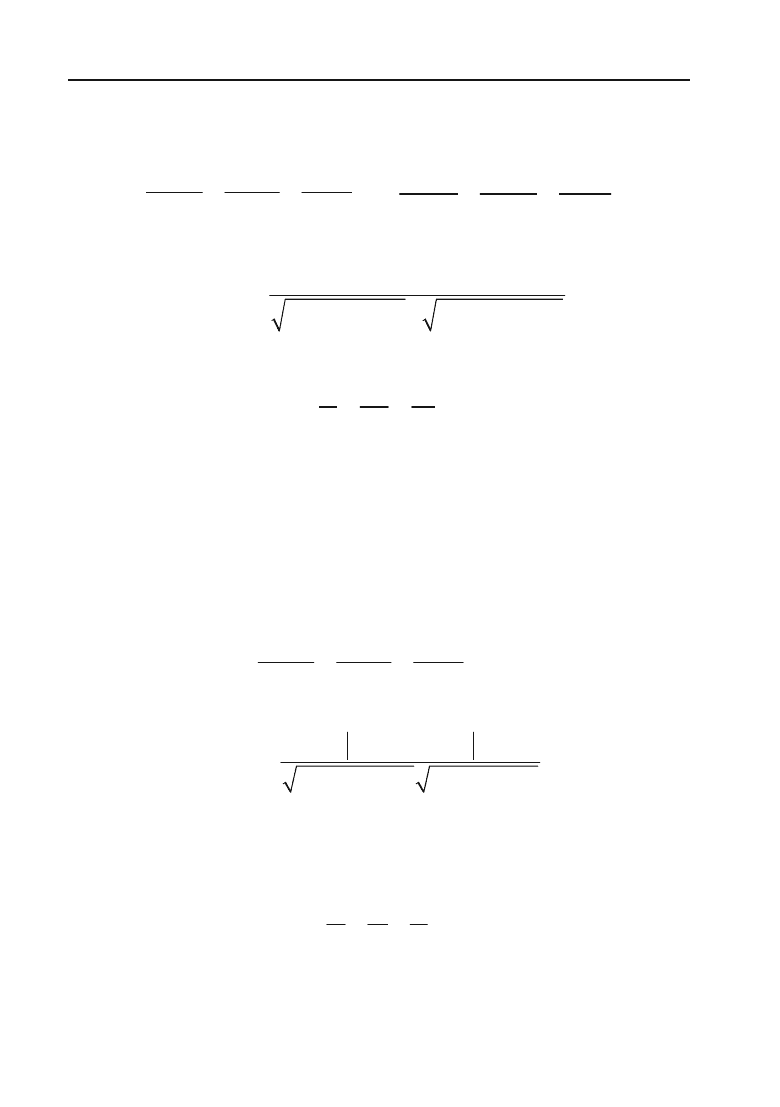
2.5.2.5. Рівняння прямої, яка проходить через дві задані точки
Рівняння прямої, що проходить через дві задані точки М
1
(х
1
; у
1
; z
1
)
і М
2
(х
2
; у
2
; z
2
) має вигляд:
111
21 21 21
x
xyyzz
x
xyyzz
. (2.36)
136
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.5.2.6. Кут між двома прямими
Кут між двома прямими
111
111
xx yy zz
lmn
і
222
222
x
xyyzz
lmn
визначається за формулою:
12 1 2 1 2
22 2 22
111 2 22
cos
*
ll mm nn
lmn lmn
M
r
. (2.37)
Умова паралельності двох прямих має вигляд:
111
222
lmn
lmn
.
Умова перпендикулярності двох прямих має вигляд:
l
1
l
2
+ m
1
m
2
+ n
1
n
2
= 0.
2.5.3. Пряма і площина
2.5.3.1. Кут між прямою та площиною
Кут між прямою
111
xx yy zz
lmn
та площиною Ax + By +
+ Cz + D = 0 визначається за формулою:
2222 22
sin
Al Bm Cn
ABClmn
M
. (2.38)
Умова паралельності прямої і площини має вигляд:
Al + Bm + Cn = 0.
Умова перпендикулярності прямої та площини має вигляд:
ABC
lmn
.

137
Розділ II. Аналітична геометрія
2.5.3.2. Точка перетину прямої і площини
Для визначення точки перетину прямої
111
xx
yy
zz
lmn
і
площини Ax + By + Cz + D = 0 необхідно розв’язати систему рівнянь:
111
0Ax By Cz D
xx yy zz
lmn
°
®
°
¯
Рівняння прямої записуємо в параметричній формі:
x = lt + x
1
; y = mt + y
1
; z = nt + z
1
.
Ці значення х, у, z підставимо в рівняння площини. З останнього
виразу знаходимо значення t:
111
Ax B
y
Cz D
t
Al Bm Cn
.
Підставляючи знайдене значення t в рівняння x = lt + x
1
, y = mt + y
1
,
z = nt + z
1
, знаходимо координати точки перетину.
2.5.3.3. Умова належності прямої площині
Умова, при якій пряма
111
xx
yy
zz
lmn
лежить в площині
Ax + By + Cz + D = 0 визначається наступними рівняннями:
111
0
0
Al Bm Cn
Ax By Cz D
®
¯
(2.39)
2.5.3.4. Умова належності двох прямих одній площині
Умовою, при якій дві прямі
111
111
xx
yy
zz
lmn
і
222
222
xx
yy
zz
lmn
лежать в одній площині, є рівність:
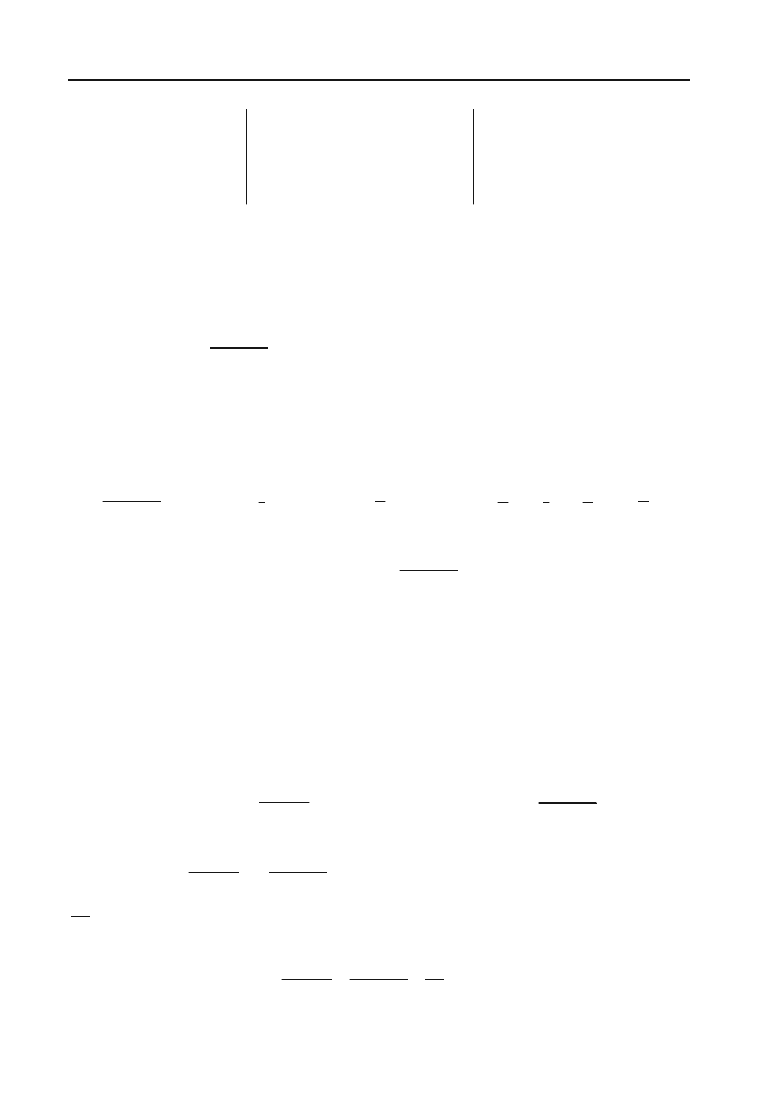
138
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.5.4. Приклади розв’язання задач
Задача 2.91. Задано дві точки М
1
(3; –1; 2) і М
2
(4; –2; –1). Скла+
сти рівняння площини, яка проходить через точку М
1
перпендику+
лярно вектору
12
MM
.
Розв’язок. Скористаємося рівнянням (2.27). Одержимо рівняння
площини, яка проходить через точку М
1
:
А(х – 3) + В(у + 1) + С(z – 2) = 0.
Нормальний вектор
12
MM
= (4 – 3)
i
+ (–2 + 1)
j
+ (–1 – 2)
k
=
i
–
j
– 3
k
=
= {1; –1; –3}.
Підставимо координати вектора
12
MM
= {1; –1; –3} замість А, В
і С в рівняння, що одержали раніше, будемо мати:
(х – 3) – (у + 1) – 3(z – 2) = 0 або х – у – 3z + 2 = 0.
Це й є шукане рівняння площини.
Задача 2.92. Знайти рівняння площини, що проходить через точ+
ки М
1
(3; 0; 4) і М
2
(5; 2; 6) перпендикулярно до площини 2х + 4у +
+ 6z – 7 = 0.
Розв’язок. Нехай точка М(х; у; z) — довільна точка шуканої пло+
щини. Тоді вектори
1
MM
= {x – 3; y – 0; z – 4} i
12
MM
= {2; 2; 2}
належать цій площині.
Вектори
1
MM
і
12
MM
компланарні з нормальним вектором
N
= {2; 4; 6} заданої площини 2х + 4у + 6z – 7 = 0. Через це міша+
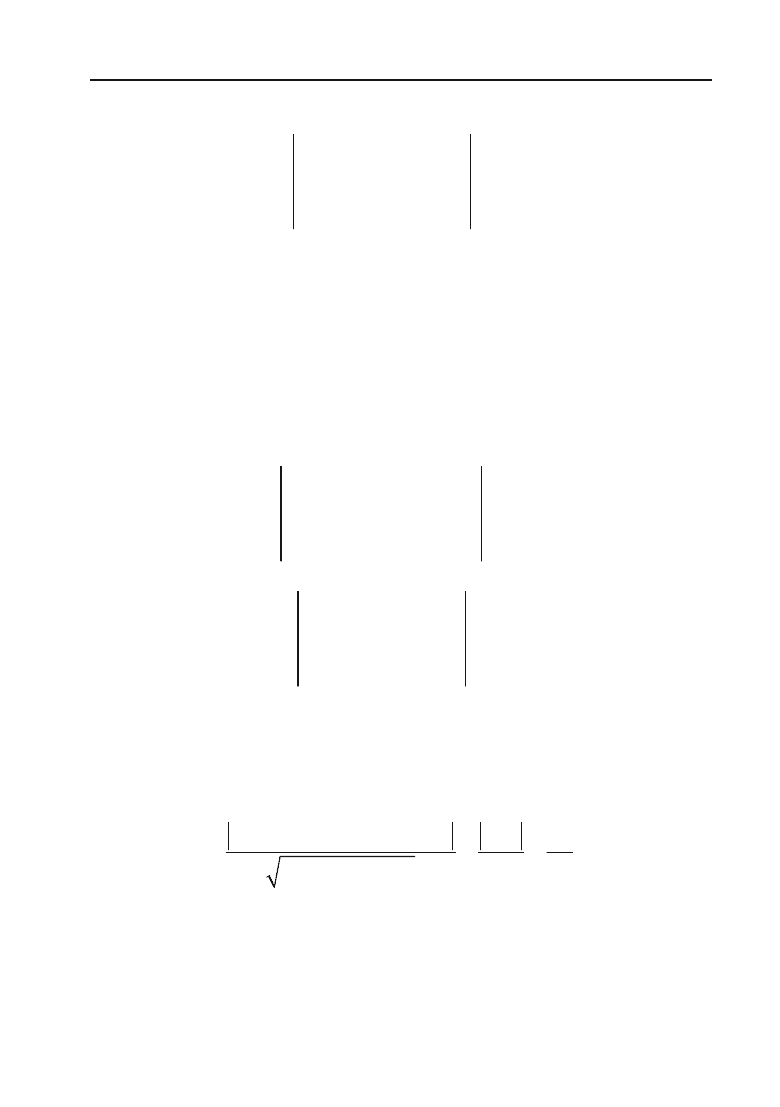
ний добуток цих трьох векторів дорівнює нулю:
(
1
MM
12
MM
N
) = 0
212121
111
222
0
xxyyzz
lmn
lmn
.
139
Розділ II. Аналітична геометрія
або
304
2220
246
xyz
.
Розв’язавши визначник, одержимо шукане рівняння площини:
х – 2у + z – 7 = 0.
Задача 2.93. Обчислити відстань d від точки Р(–1; 1; –2) до
площини, що проходить через три точки М
1
(1; –1; 1), М
2
(–2; 1; 3) і
М
3
(4; –5; –2).
Розв’язок. Складемо рівняння площини, що проходить через три
задані точки М
1
(1; –1; 1), М
2
(–2; 1; 3) і М
3
(4; –5; –2). Використаємо
формулу (2.23):
111
21 11 31 0
41 51 21
xyz
;
111
32 20
343
xyz
.
Розкривши визначник, одержимо рівняння площини
2х – 3у + 6z – 11 = 0.
А тепер обчислимо відстань d від точки Р(–1; 1; –2) до площини
2х – 3у + 6z – 11 = 0. Використаємо формулу (2.32):
222
2( 1) 3(1) 6( 2) 11 28
28
4
77
2(3)6
d
.
d = 4 (од. довж.).
Задача 2.94. Скласти рівняння площини, що проходить через
точку перетину трьох площин 2х – у – z – 1 = 0, х + 2z – 4 = 0,
х – у = 0, через початок координат і через точку Р(7; 1; 2).

140
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розв’язок. Знайдемо точку перетину трьох заданих площин. Для
цього розв’яжемо систему рівнянь:
210,
240,
0.
xyz
xz
xy
°
®
°
¯
Знайдемо визначник системи:
211
10 2
110
'
= 1 – 2 + 4 = 3.
Знайдемо визначник
x
' :
111
40 2
010
x
'
= 4 + 2 = 6.
Таким чином:
6
2
3
x
x
x
'
; х = 2.
Із третього рівняння системи знайдемо, що
у = х, у = 2.
Із другого рівняння системи знаходимо z:
442
1
22
x
z
, z = 1.
Точка перетину трьох заданих площин М(2; 2; 1).
Для знаходження рівняння шуканої площини використаємо фор+
мулу (2.23).
000
20 20 10 0
70 10 20
xyz
.
