Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


151
Розділ II. Аналітична геометрія
2.6.1. Приклади розв’язання задач.
Задача 2.121. Побудувати область розв’язків системи лінійних
нерівностей:
12
1
12
12
25 10;
3;
3312;
212.
xx
x
xx
xx
t
°
d
°
®
d
°
°
t
¯
Розв’язок. Будуємо граничні прямі, що відповідають даним не+
рівностям, за двома точками, що відповідають цим прямим:
(l
1
): 2х
1
– 5х
2
= –10, A
1
(0; 2)
l
1
, A
2
(–5; 0)
l
1
;
(l
2
): x
1
= 3;
(l
3
): 3х
1
+ 3х
2
= 12, B
1
(0; 6)
l
3
, B
2
(4; 0)
l
3
;
(l
4
): х
1
+ 2х
2
= –12, C
1
(0; –1)
l
4
, C
2
(–2; 0)
l
4
.
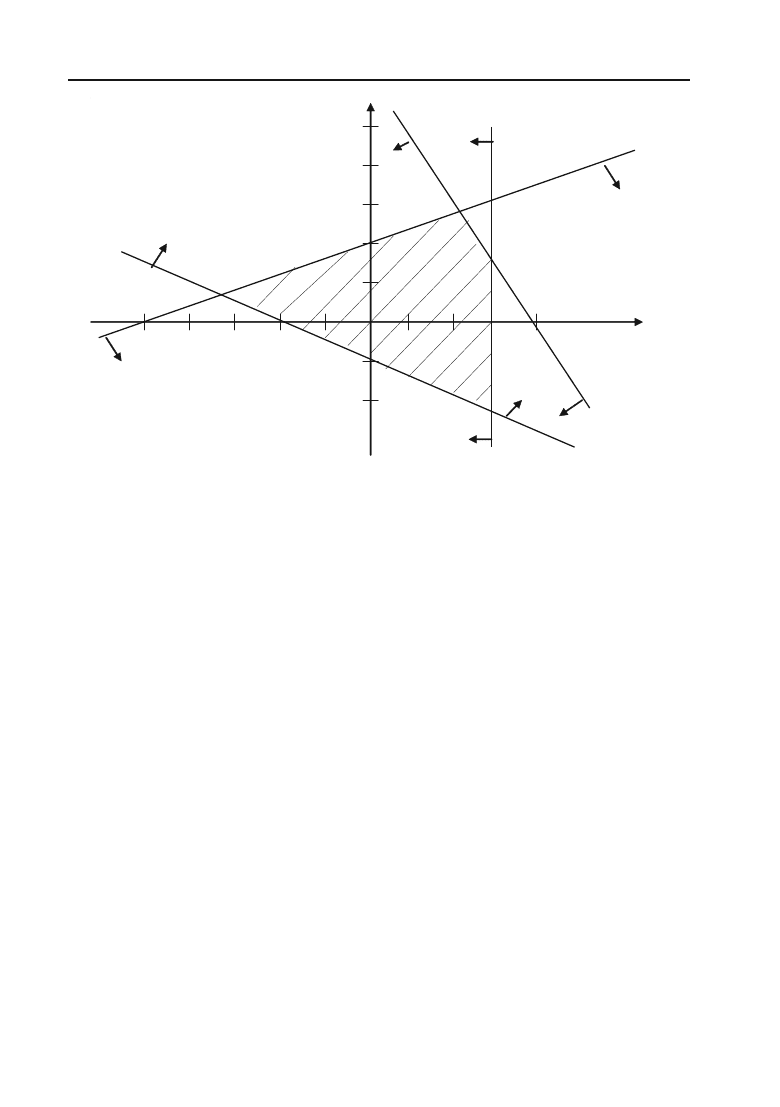
Кожна пряма ділить площину на дві півплощини. Та з них, що
містить початок координат, і є областю розв’язків кожної з нерівно+
стей (координати точки О(0; 0) задовольняють кожній нерівності).
Стрілками позначимо півплощини, які є областями розв’язків даних
нерівностей. Перетин відмічених півплощин — чотирикутник АВСD —
є область розв’язків даної системи (рис. 2.21).
Задача 2.122. Побудувати область розв’язків системи лінійних
нерівностей:
11
12
2
6;
3515;
1.
xx
xx
x
d
°
t
®
°
t
¯
Аналогічно інтерпретуються геометрично лінійні нерівності з
трьома змінними. Лінійна нерівність з трьома невідомими визначає
півпростір, а система таких нерівностей – переріз півпростору. Якщо
він не порожній, є многогранною областю або, в випадку обмеже+
ності, многогранником.
152
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розв’язок. Будуємо граничні прямі, що відповідають даним не+
рівностям:
(l
1
): –х
1
+ х
1
= 6, A
1
(0; 6)
l
1
, A
2
(–6; 0)
l
1
;
(l
2
): 3х
1
+ 5х
2
= 15, B
1
(0; 3)
l
2
, B
2
(5; 0)
l
2
;
(l
3
): x
2
= 1.
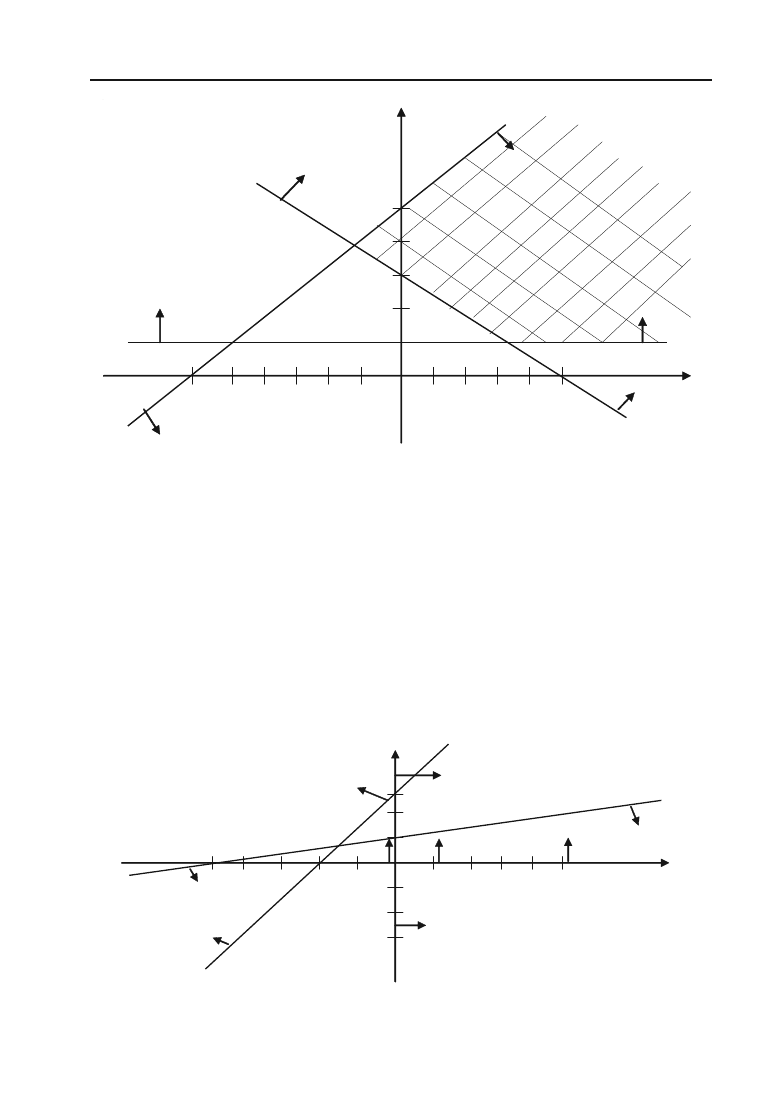
Область розв’язків першої прямої містить початок координат, а
область розв’язків другої і третьої нерівностей — не містять початку
координат (координати точки О(0; 0) не задовольняють другій і третій
нерівностям). Стрілками позначимо півплощини, точки яких задо+
вольняють нерівностям. Областю розв’язків є опукла необмежена
область (рис. 2.22).
Задача 2.123. Побудувати область розв’язків системи лінійних
нерівностей:
12
12
1
2
32 6;
55;
0;
0.
xx
xx
x
x
d
°
d
°
®
t
°
°
t
¯
–5 –2 О 3 4 Х
1
Х
2
5
2
–1
(l
2
)
(l
1
)
(l
3
)
(l
4
)
A
B
C
D
Рис. 2.21.
153
Розділ II. Аналітична геометрія
Розв’язок. Будуємо граничні прямі:
(l
1
): 3х
1
– 2х
2
= 6, A
1
(0; 6)
l
1
, A
2
(–6; 0)
l
1
;
(l
2
): –х
1
+ 5х
2
d
5, B
1
(0; 1)
l
2
, B
2
(–5; 0)
l
2
;
(l
3
): х
1
= 0;
(l
4
): х
2
= 0.
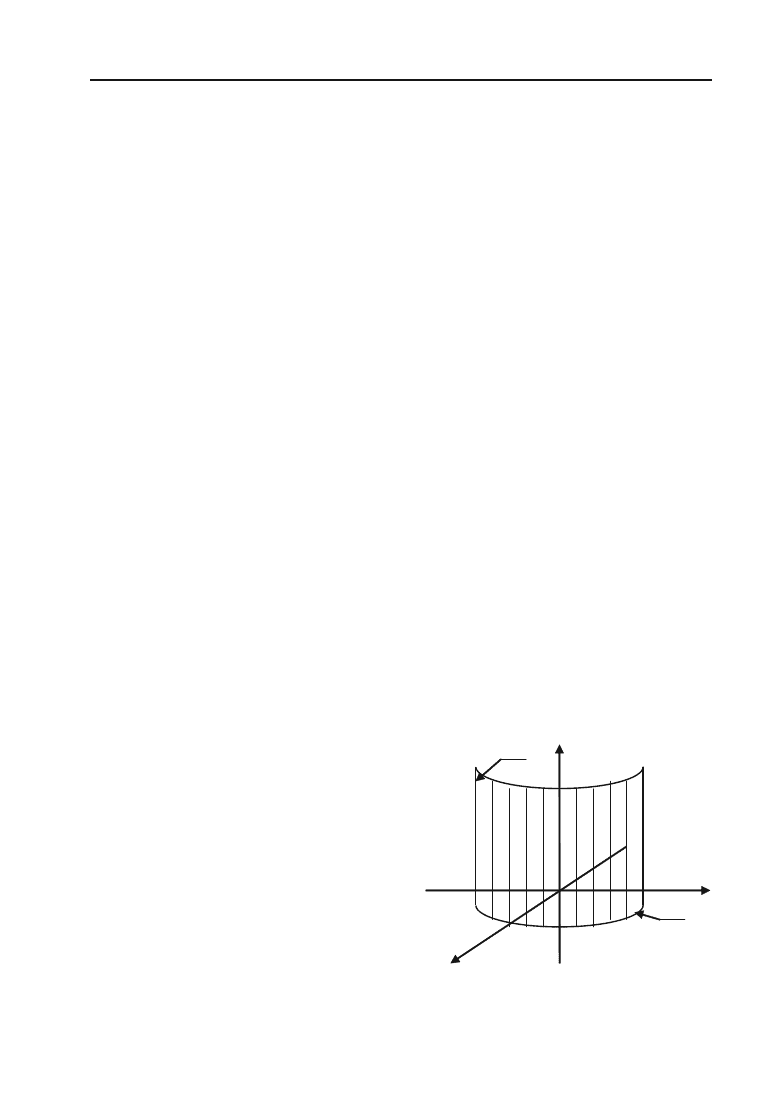
Будуємо область розв’язків кожної нерівності (рис. 2.23).
Не існує жодної точки, загальної для всіх площин, що відповіда+
ють даним рівнянням. Отже, область розв’язків порожня. Система
нерівностей несумісна.
Рис. 2.22.
–6 О 5 Х
1
Х
2
5
3
1
(l
1
)
(l
2
)
(l
3
)
Рис. 2.23.
–5 –2 О Х
1
Х
2
3

154
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.6.2. Задачі для самостійного розв’язку
2.124. Побудувати області, координати яких задовольняють не+
рівностям:
а) у < 2 – x, x > –2, y > –2.
б) y > 2 – x, x < 4, y < 0.
в)
1
42
xy
d
, y
t
x + 2, x
t
–4.
2.125. Побудувати область розв’язків системи лінійних нерівно+
стей:
а)
12
12
1
2
7,
23 4,
1,
0;
xx
xx
x
x
d
°
d
°
®
t
°
°
t
¯
б)
12
12
1
2
24,
24,
0,
0;
xx
xx
x
x
t
°
t
°
®
t
°
°
t
¯
в)
12
1
2
44,
0,
0;
xx
x
x
d
°
t
®
°
t
¯
г)
12
12
12
23 13,
6,
416;
xx
xx
xx
d
°
t
®
°
d
¯
д)
12
12
12
1
2
26,
38,
3,
0,
0;
xx
xx
xx
x
x
t
°
t
°
°
d
®
°
t
°
°
t
¯
е)
12
12
12
1
2
210,
22,
210,
0,
0.
xx
xx
xx
x
x
d
°
t
°
°
d
®
°
t
°
°
t
¯
155
Розділ II. Аналітична геометрія
§ 2.7. Поверхні другого порядку
Означення. Поверхнею другого порядку називають геометрич+
не місце точок простору, декартові координати яких задовольняють
рівнянню другого степеня.
2.7.1. Сфера та її рівняння
Сферою називається геометричне місце точок простору, рівновід+
далений від заданої точки+центра сфери.
Якщо центр сфери є точка С(a; b; c), а радіус R, тоді рівняння
сфери буде:
(x – a)
2
+ (y – b)
2
+ (z – c)
2
= R
2
.
(2.43)
Якщо центр сфери знаходиться в початку координат О(0; 0; 0) і
радіус є R, тоді рівняння сфери буде:
x
2
+ y
2
+ z
2
= R
2
.
2.7.2. Циліндричні поверхні
Поверхня називається циліндричною, якщо вона утворена пря+
мою (твірна), паралельною до заданої прямої а і яка проходить через
задану лінію l (напрямна лінія). Приклад циліндричної лінії зобра+
жено на рис. 2.24.
Якщо твірна циліндричної поверхні паралельна осі Оz, а напрям+
на l лежить в площині хОу
і задана рівнянням:
(,) 0
0
Fxy
Z
®
¯
тоді рівняння циліндричної по+
верхні буде:
(,) 0
(;)
Fxy
Z
®
ff
¯
Рівняння F(x, z) = 0 визначає
циліндричну поверхню з твірною,
що паралельна осі Оу, рівняння
aZ
l
Y
O
X
Рис. 2.24.
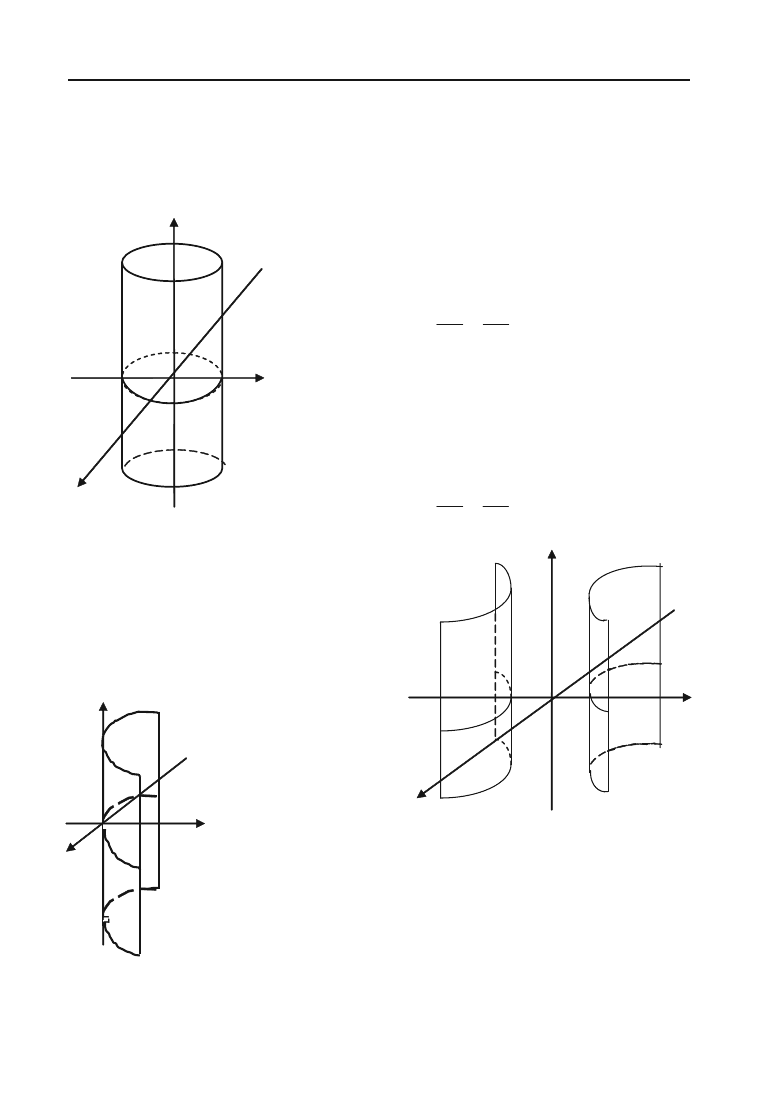
156
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
F(y, z) = 0 — циліндричну поверхню з твірною, що паралельна
осі Ох.
2.7.3. Циліндри другого порядку
а) Еліптичним циліндром називається
поверхня (рис. 2.25), канонічне рівняння якої
має вигляд
22
22
1
xy
ab
.
Якщо а = b, то маємо круговий циліндр:
х
2
+ у
2
= а
2
.
б)
Гіперболічним циліндром називається
поверхня, рівняння якої має вигляд (рис. 2.26):
22
22
1
xy
ab
.
в)
Параболічним циліндром на+
зивається поверхня, канонічне
рівняння якої має вигляд (рис. 2.27):
у
2
= 2pх.
2.7.4. Еліпсоїд
Еліпсоїдом називається поверхня, канонічне
(найпростіше) рівняння якої має вигляд (рис.
2.28):
О
Y
Z
X
Рис. 2.26.
Y
X
О
Z
Рис. 2.25.
Z
X
Y
O
Рис. 2.27.
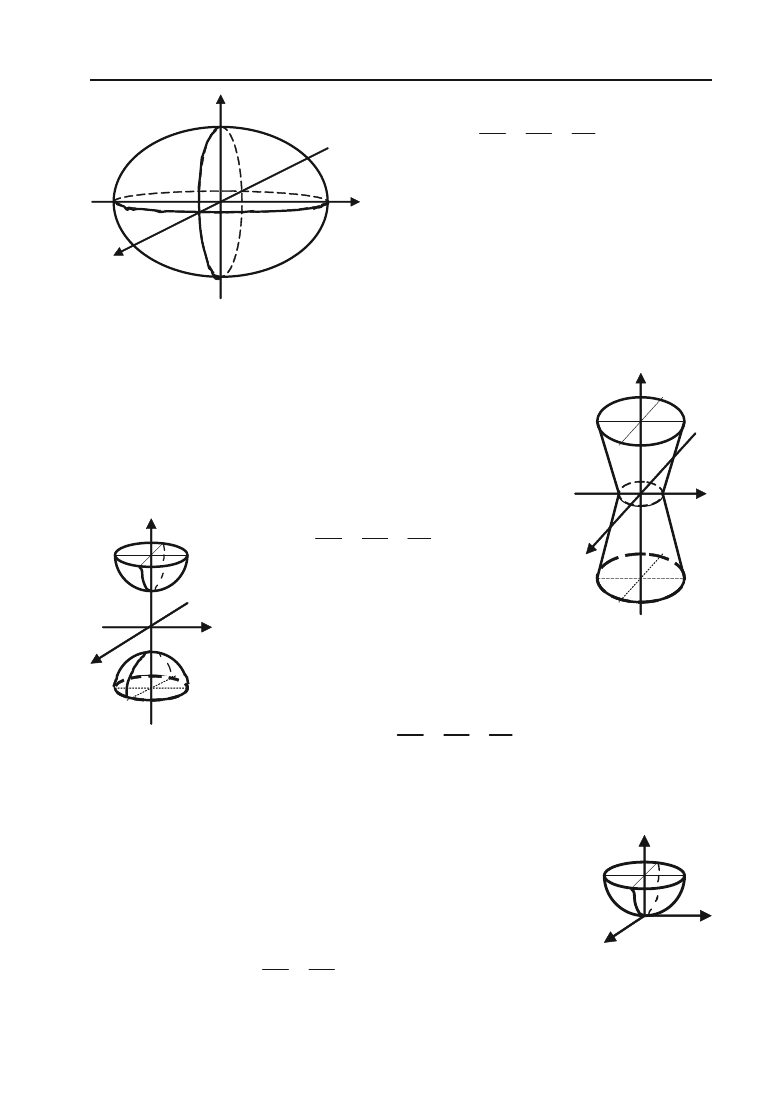
157
Розділ II. Аналітична геометрія
222
222
1
xyz
abc
Відрізки а, b, с — називаються
півосями еліпсоїда.
2.7.5. Гіперболоїди
а) Однопорожнинний гіперболоїд.
Однопорожнинним гіперболоїдом (рис. 2.29)
називається поверхня, канонічне (найпростіше)
рівняння якої має вигляд:
222
222
1
xyz
abc
.
б) Двохпорожнинний гіпер+
болоїд.
Двохпорожнинним гіпербо,
лоїдом
(рис. 2.30) називається
поверхня, канонічне рівняння якої має вигляд:
222
222
1
xyz
abc
.
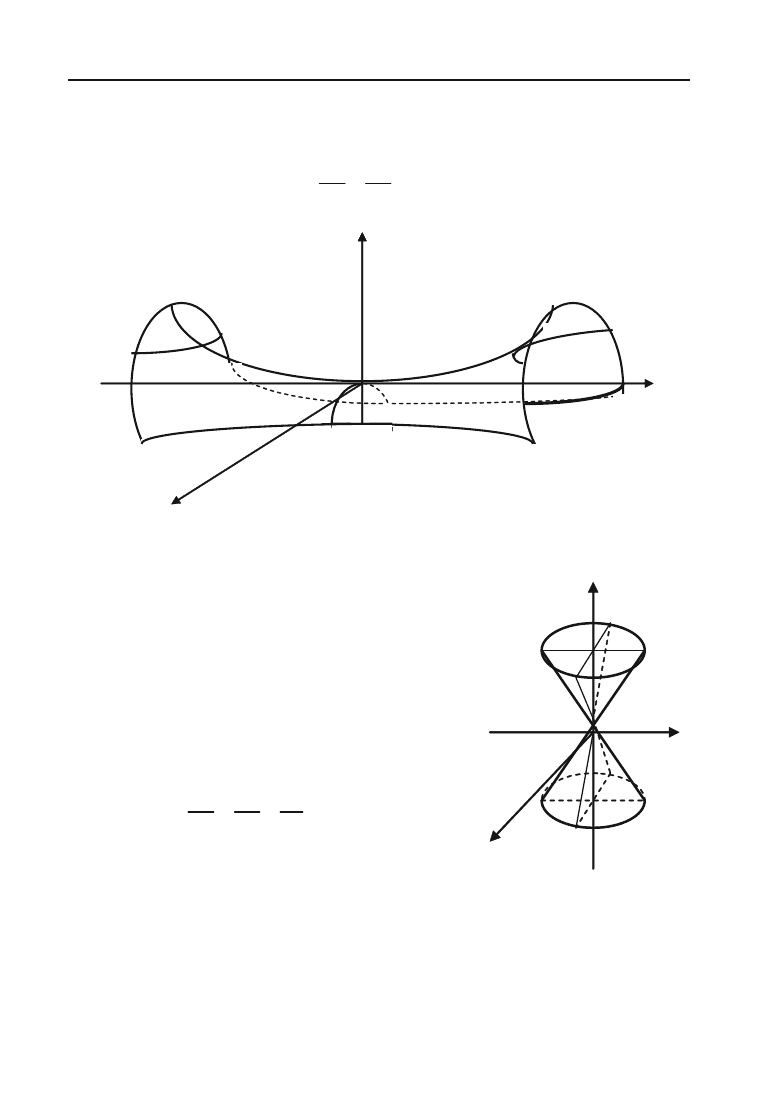
2.7.6. Параболоїди
а)
Еліптичним параболоїдом (рис. 2.31) нази+
вається поверхня, канонічне (найпростіше) рівнян+
ня якої має вигляд:
22
2
xy
z
pq
.
Z
X О Y
Рис. 2.30.
Рис. 2.28.
О
Y
X
Z
Рис. 2.30.
Y X
Z
О
Z
О
Y
X
Рис. 2.29.
158
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
б) Гіперболічним параболоїдом (рис. 2.32) називається поверх+
ня, канонічне (найпростіше) рівняння якої має вигляд:
22
2
xy
z
pq
.
Рис. 2.32.
Y
X
Z
2.7.7. Конічні поверхні
Конічною поверхню називається повер+
хня, яка описана прямою, що проходить
через точку – вершину конуса – і що пере+
тинає задану лінію – напрямну конуса.
Рівняння конуса (рис. 2.33) другого поряд+
ку має вигляд:
222
222
0
xyz
abc
.
2.7.7. Поверхні обертання
Нехай в площині xOz задана лінія l, що має рівняння F(x, z) = 0.
Тоді щоб одержати рівняння поверхні, що утворена обертанням лінії
Рис. 2.33.
О
X
Y
Z

159
Розділ II. Аналітична геометрія
l, що лежить в площині xOz навколо осі Ох, треба в рівняння цієї
лінії замінити z на
22
y
z
r
. Шукане рівняння поверхні обертання
буде F(x,
22
y
z
r
) = 0.
Аналогічні правила будуть мати місце і по відношенню до повер+
хонь, які утворюються обертанням плоских ліній навколо інших
координатних осей.
Приклади: 1) Рівняння поверхні, що утворюється обертанням
еліпса
22
22
1
xz
ac
навколо осі Ох, буде
222
22
1
xzy
ac
(еліпсоїд
обертання).
2) Рівняння поверхні, що утворюється обертанням гіперболи
22
22
1
xz
ac
навколо осі Ох буде
222
22
1
xzy
ac
, або
22 2
222
1
yzx
cca
(двохпорожнинний гіперболоїд).
2.7.8. Приклади розв’язання задач
Задача 2.126. Визначити координати центра сфери і її радіус
х
2
+ у
2
+ z
2
– 6x + 8y + 10z + 25 = 0.
Розв’язок. Представимо задане рівняння в вигляді (2.43), для цього:
1) об’єднаємо в групи члени, які містять однойменні координати;
2) виділимо в групах повні квадрати (ми раніше так само визна+
чали координати центра кола і його радіус). Одержимо:
х
2
– 6х + у
2
+ 8у + z
2
+ 10z + 25 = 0;
х
2
– 2
3х + 3
2
– 3
2
+ у
2
+ 2
4у + 4
2
– 4
2
+ z
2
+ 25z + 5
2
– 5
2
+25= 0;
(х – 3)
2
– 9 + (у + 4)
2
– 16 + (z + 5)
2
– 25 + 25 = 0;
(х – 3)
2
+ (у + 4)
2
+ (z + 5)
2
= 25.
Порівнюючи з (2.43), маємо а = 3, b = –4, с = –5, R
2
= 25. Отже,
центр сфери — точка С(3; –4; –5), радіус R = 5.
Задача 2.127. Еліпс з півосями 5 та 3 обертається навколо своєї
великої осі, яка співпадає з початком координат. Скласти рівняння
поверхні, що описує еліпс при обертанні.
Розв’язок. Складемо канонічне рівняння еліпса з центром в по+
чатку координат, який розміщений в площині yOz: а = 5, b = 3.

160
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
22
1
25 9
0
yz
x
°
®
°
¯
.
Щоб одержати рівняння поверхні, яка утворена обертанням елі+
пса, що розміщений в площині yOz, навколо осі Оу, необхідно в
рівняння еліпса замінити z на
22
x
z
r
. Одержуємо еліпсоїд обер+
тання, який витягнуто вздовж осі Оу:
222
1
25 9
yxz
, або
222
1
9259
xyz
.
Задача 2.128. Скласти рівняння конуса з вершиною в початку
координат і напрямною:
222
,
.
x
ya
zc
®
¯
Розв’язок. Канонічні рівняння твірних, що проходять через вер+
шину О(0; 0; 0) конуса і точку (х; у; z) напрямної, будуть:
X
YZ
x
yz
.
Виключимо х, у, z із заданих рівнянь. Замінюючи z через с, виз+
начимо х і у із останніх двох рівнянь:
X
xc
z
,
Y
y
c
z
.
Підставимо одержані значення х і у в перше рівняння напрямної,
будемо мати:
22 22
2
22
cX cY
a
z
z
, або
222
22
0
xyz
ac
.
Задача 2.129. Які поверхні визначаються рівняннями:
1) x
2
+ z
2
= 16; 2)
22
1
64
xz
; 3) x = 2z
2
; 4)
22
1
57
xz
.
