Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

141
Розділ II. Аналітична геометрія
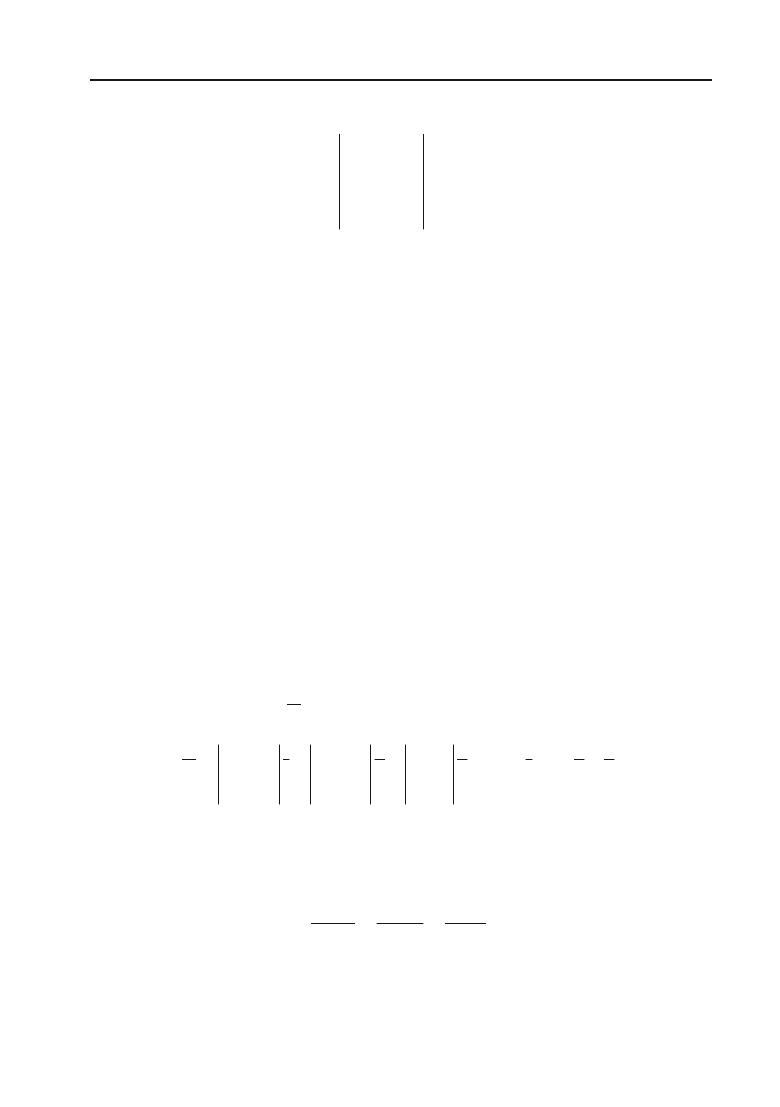
Спростивши, маємо:
2210
712
xyz
.
Розкривши визначник, одержимо рівняння шуканої площини:
х + у – 4z = 0.
Задача 2.5.95. Знайти канонічне рівняння прямої:
32411,
231.
xyz
xy z
®
¯
Розв’язок. Нехай х
1
= 1, тоді маємо:
312411 248,
21 3 1 3 1.
yz yz
yz yz
®®
¯¯
Від першого рівняння віднімемо друге, помножене на 2:
248,
26 2.
yz
yz
®
¯
10z = 10, z
1
= 1.
у = 1 + 3z – 2х, у = 1 + 3 – 2 = 2, у
1
= 2.
Отримали точку площини М
1
(1; 2; 1).
Знайдемо вектор
S
:
24 43 32
10 17
13 32 21
Sijkijk
.
Маємо l = –10, m = 17, n = –1.
Користуючись формулою (2.34), одержуємо канонічне рівняння
прямої:
121
10 17 1
xyz
.
Задача 2.96. Скласти канонічне та параметричне рівняння, що
проходять через точки М
1
(3; –5; 2) та М
2
(1; –1; –4).
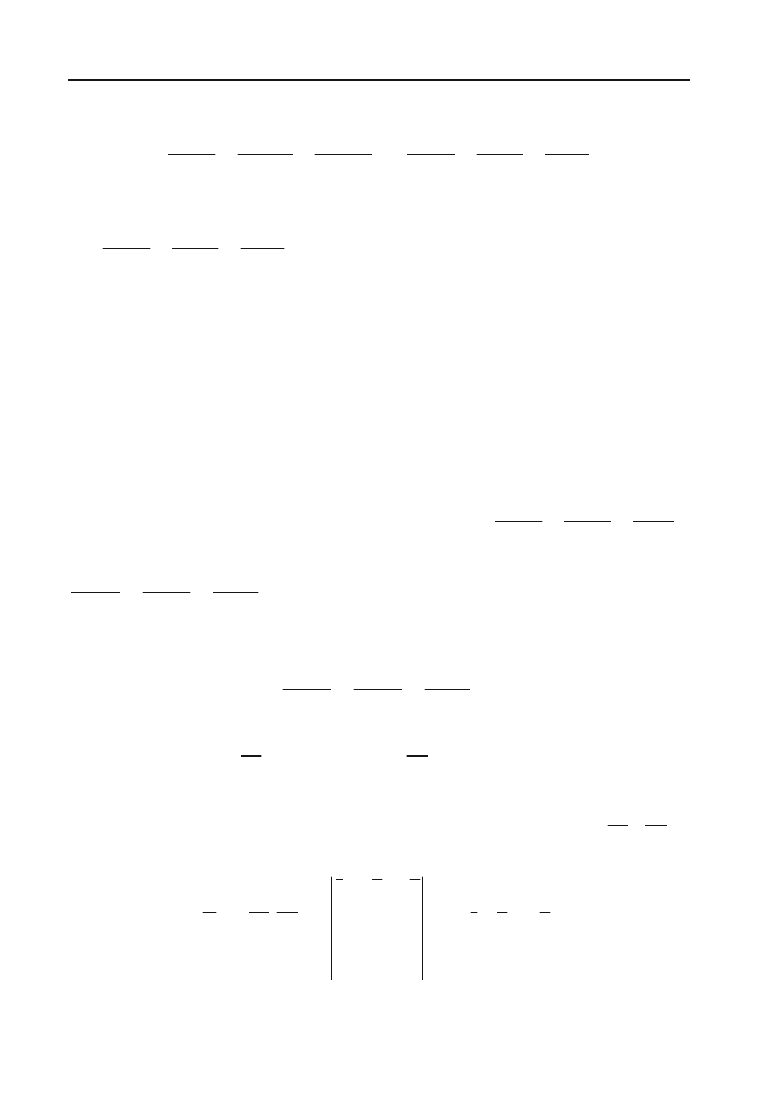
142
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розв’язок. За формулою (2.36) маємо:
35 2
13 15 42
xy z
352
24 6
xyz
або
352
123
xyz
— це канонічне рівняння прямої.
Для знаходження параметричного рівняння цієї прямої викорис+
таємо формулу (2.35), тоді одержимо:
3,
52,
23.
x
t
y
t
z
t
°
®
°
¯
(
;
)
t
ff
Задача 2.97. Скласти рівняння прямої, що проходить через точ+
ку М
1
(2; –3; 4) і перпендикулярно до прямих
231
111
xy
z
і
404
213
xyz
.
Розв’язок. Рівняння шуканої прямої є:
234xyz
lmn
.
Задані прямі мають напрямні вектори:
1
S
= {1; –1; 1} i
2
S
= {2; 1; 3}.
Так як шукана пряма перпендикулярна до заданих прямих, то за
напрямний вектор її можна прийняти векторний добуток
12
SSu
:
12
S1114 2
213
ijk
SS ijk
ªº
¬¼
,

143
Розділ II. Аналітична геометрія
або
S
= {l; m; n} = {–4; –1; 2}.
Звідси буде, що координати напрямного вектора шуканої прямої
дорівнюють: l = –4, m = –1, n = 2.
Шукана пряма має рівняння:
234
412
xyz
,
або
234
41 2
xyz
.
Задача 2.98. Знайти координати точки перетину прямої
122
211
xyz
з площиною 3х – у + 2z + 5 = 0.
Розв’язок. Представимо рівняння прямої в параметричній формі.
Прирівняємо кожне з співвідношень, які входять в рівняння прямої,
до параметра t:
1
2
x
t
;
2
1
y
t
;
2
1
z
t
;
x = 2t + 1; y = t – 2; z = t + 2.
Підставимо ці значення х, у, z в рівняння площини:
3(2t + 1) – (t – 2) + 2(t + 2) + 5 = 0,
6t + 3 – t + 2 + 2t + 4 + 5 = 0,
7t + 14 = 0,
t = –2.
Одержане значення t = –2 є значенням параметру в точці пере+
тину прямої з площиною. Підставляємо це значення в параметричні
рівняння прямої:
x = 2t + 1; y = t – 2; z = t + 2,
одержуємо:
х = 2(–2) + 1 = –3, у = –2 – 2 = –4, z = –2 + 2 = 0 — точку перетину
прямої з площиною.
Отже, пряма перетинає площину в точці М(–3; –4; 0).

144
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Задача 2.99. Знайти проекцію точки М(2; –1; 3) на площину
х + 3у – 4z –13 = 0.
Розв’язок.
а) Складено рівняння прямої, що проходить через точку М(2; –1; 3)
перпендикулярно до площини х + 3у – 4z – 13 = 0. Спочатку напи+
шемо рівняння прямої, що проходить через точку М(2; –1; 3):
213xyz
lmn
.
На основі умови перпендикулярності прямої і площини
ABC
lmn
числа l, m, n пропорційні числам А, В, С із рівняння
площини. Через це, замінивши в останньому рівнянні l, m, n числа+
ми 1, 3, –4, одержуємо рівняння прямої в вигляді:
213
13 4
xyz
.
б) Щоб знайти проекцію точки на площину, необхідно знайти
координати основи перпендикуляра, проведеного із точки М на пло+
щину, тобто точку перетину прямої з площиною.
213
,
13 4
34130.
xyz
xyz
°
®
°
¯
Рівняння прямої
213
13 4
xyz
представляємо в парамет+
ричній формі. Одержимо: x = t + 2, y = 3t – 1, z = –4t + 3. Одержані
значення х, у, x підставляємо в рівняння площини:
t + 2 + 3(3t – 1) – 4(–4t + 3) – 13 = 0,
t + 2 + 9t – 3 + 16t – 12 – 13 = 0,
26t – 26 = 0, t = 1.
Значення параметра t = 1 підставимо в рівняння
x = t + 2, y =3t – 1, z = –4t + 3.
Маємо:

145
Розділ II. Аналітична геометрія
x = 1 + 2 = 3, y = 3
1 – 1 = 2, z = –4
1 + 3 = –1.
Отже, проекція точки на площину є точка М
1
(3; 2; –1).
Задача 2.100. Скласти рівняння площини, що проходить через
точку М
1
(1; 1; –2) і пряму
13
215
xyz
.
Розв’язок. В шуканій площині повинні знаходиться точка
М
1
(1; 1; –2) та пряма
13
215
xyz
. Виберемо в шуканій пло+
щині точку М(х; у; z). Якщо пряма
13
215
xyz
лежить в шу+
каній площині, то точка Р(1; 3; 0) заданої прямої знаходиться в пло+
щині, а напрямний вектор
S
= {2; –1; 5} паралельний шуканій
площині. Розглянемо вектори:
1
MM
= {x – 1; y – 1; z + 2},
1
MP
= {1 – 1; 3 – 1; 0 + 2} та
S
= {2; –1; 5}. Ці вектори компла+
нарні, а це означає, що їх мішаний добуток дорівнює нулю:
1
MM
1
MP
S
= 0,
або
112
0220
215
xyz
.
Розкриваємо визначник:
10(х – 1) + 0(z + 2) + 4(y – 1) – 4(z + 2) – 2(x – 1) – 0(y – 1) = 0;
8(x –1) + 4(y – 1) – 4(z + 2) = 0;
2(x – 1) + (y – 1) – (z + 2) = 0;
2x + y – z – 5 = 0.
Ми отримали рівняння шуканої площини.

146
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.5.5. Задачі для самостійного розв’язку.
2.101. Скласти рівняння площини, що проходить через точку
М
1
(2; 5; –1) і паралельна площині х + 3у – 4z + 5 = 0.
2.102. Задані точки М
1
(0; –1; 3) і М
2
(1; 3; 5). Скласти рівняння
площини, що проходить через точку М
1
і перпендикулярна до векто+
ра
12
NMM
.
2.103. Знайти рівняння площини, що проходить через точку
М(2; –1; 3) і відтинає на осях координат рівні відрізки.
2.104. Знайти рівняння площини, що проходить через точки
М
1
(1; –1; 2), М
2
(2; 1; 2) і М
3
(1; 1; 4).
2.105. Знайти відстань від точки Р(4; 3; 0) від площини, що про+
ходить через точки М
1
(1; 3; 0), М
2
(4; –1; 2) і М
3
(3; 0; 1).
2.106. Скласти рівняння площини, що проходить через точку
Р(1; 2; 3) і перпендикулярної до площин х – у + z – 7 = 0, 3х + 2у –
– 12z + 5 = 0.
2.107. Знайти точку перетину площин:
2х – у + 3z – 9 = 0; х + 2у + 2z – 3 = 0; 3х + у – 4z + 6 = 0.
2.108. Скласти рівняння перпендикуляру, який опущений із точ+
ки М(2; –3; 4) на вісь Оz.
2.109. Привести до канонічного виду рівняння прямої, яке задано:
3450
20
xyz
xyz
®
¯
.
2.110. Знайти кут між прямими
121
23 6
xyz
і
2420
4540
xy z
xy z
®
¯
.
2.111. Знайти точку перетину прямої
11
126
xyz
з площи+
ною 2х + 3у + z – 1 = 0.
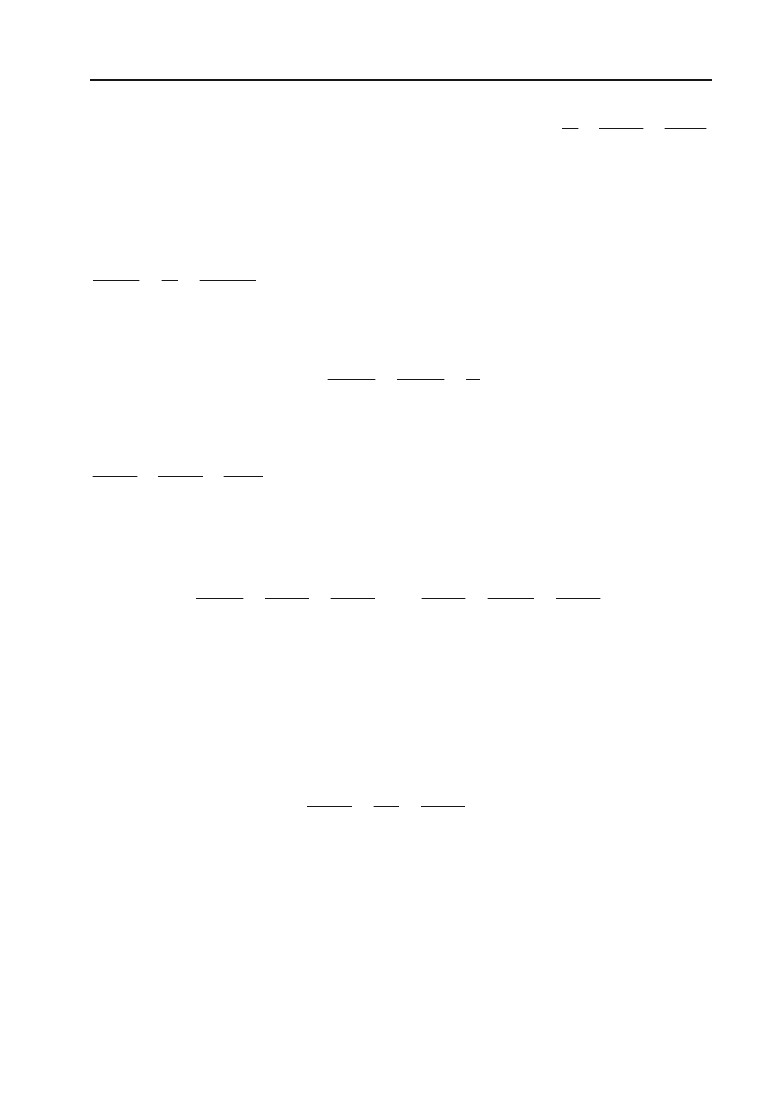
147
Розділ II. Аналітична геометрія
2.112. Знайти проекцію точки Р(2; –1; 3) на пряму
72
35 2
x
y
z
.
2.113. Знайти проекцію точки Р(5; 2; –1) на площину 2х – у + 3z +
+23 = 0.
2.114. Обчислити відстань d від точки Р(2; 3; –1) до прямої
525
32 2
xyz
.
2.115. Скласти рівняння площини. яка проходить через точку
Р(3; 1; –2) і через пряму
43
521
xyz
.
2.116. Скласти рівняння площини, яка проходить через пряму
231
512
xyz
і перпендикулярну до площини х + 4у – 3z + 7 = 0.
2.117. Скласти рівняння площини, що проходить через дві пара+
лельні прямі
213
32 2
xyz
і
123
32 2
xyz
.
2.118. Знайти точку Q, що симетрична точці Р(1; 3; –4) відносно
площини 3х + у – 2z = 0.
2.119. Знайти точку Q, що симетрична точці Р(2; –5; 7) відносно
прямої, що проходить через дві точки М
1
(5; 4; 6) і М
2
(–2; –17; –8).
2.120. Скласти рівняння перпендикуляра, який опущений із точ+
ки Q(2; 3; 1) на пряму
12
213
xyz
.

148
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§ 2.6. Нерівності та їх геометричний зміст
Метод координат дозволяє геометрично тлумачити не тільки
рівняння, а також і нерівності.
Подібно тому, як ми говоримо, що рівняння з двома змінними х
та у F(x, y) = 0 визначає на площині деяку лінію, можна сказати, що
нерівність з двома змінними х та у F(x, y) < 0 визначає множину
точок площини, координати яких задовольняють цій нерівності. Та+
ким чином геометрично тлумачать і нерівність F(x, y) > 0.
Якщо вираз F(x, y) є лінійним, тобто F(x, y) = Ах + Ву + С, де А,
В, С – сталі, то ми маємо лінійне рівняння
Ах + Ву + С = 0, (2.40)
та дві лінійні нерівності
Ах + Ву + С < 0, (2.41)
Ах + Ву + С > 0. (2.42)
Якщо коефіцієнти А і В не дорівнюють одночасно нулю, то рівнян+
ня (2.40) визначає на площині пряму, а нерівності (2.41) і (2.42) —
відповідно дві півплощини, на які пряма (2.40) розбиває всю коор+
динатну площину. Для того щоб з’ясувати, яка із цих двох півпло+
щин визначається заданою лінійною нерівністю, можна застосувати,
наприклад, такий спосіб.
Виберемо яку+небудь точку, підставляємо її координати в
нерівність, що перевіряється.
Якщо координати точки задовольняють нерівність, то нерівність
визначає ту площину, в якій знаходиться вибрана точка; якщо ж
координати точки не задовольняють нерівність, то нерівність визна+
чає площину, яка не містить вибраної точки.
Приклад. Записати з допомогою нерівності ту півплощину, в якій
лежить точка М(4; 5) та границею якої є пряма 3х – 2у + 5 = 0.
Перевірити, лежить в цій же півплощині початок координат.
Розв’язок. Підставимо координати точки М в ліву частину рівнян+
ня заданої прямої: 3
4 – 2
5 + 5 = 7. Одержана величина додатна.
Отже, точка М не лежить на заданій прямій, а шукана площина виз+
начається нерівністю 3х – 2у + 5 > 0.
Студенту рекомендовано зробити малюнок і розв’язати самостійно
другу частину приклада.

149
Розділ II. Аналітична геометрія
Можна розглянути також систему нерівності:
1
2
(,) 0
(,) 0
... ... ... ...
(,) 0
m
Fxy
Fxy
Fxy
°
°
®
°
°
¯
Областю розв’язання системи нерівностей називається множина
всіх точок, координати кожної із них задовольняють всім нерівнос+
тям системи.
Перерізом кількох множин точок називається множина точок,
кожна із яких належить всім множинам, що перетинаються. Очевид+
но, областю розв’язання системи нерівностей служить переріз обла+
стей розв’язання кожної із нерівностей системи.
Областю розв’язків, системи лінійних нерівностей
111
222
0,
0,
... ... ... ... ...
0,
mmm
Ax By C
Ax By C
Ax By C
°
°
®
°
°
¯
є, очевидно переріз півплощин, що визначаються кожною із нерівно+
стей системи. Ця область може бути і пустою множиною, тобто мно+
жиною, яка не містить ні одної точки (півплощини не мають спільних
точок).
Якщо ж ця множина точок не пуста, то вона називається много+
кутною областю. Якщо, крім того, ця область обмежена, тобто на
містить точок з як завгодно великим значенням координат, то її на+
зивають многокутником.
Приклад. Записати з допомогою системи нерівностей множину
точок, що лежать всередині трикутника з вершинами А(2; 1), В(6; 3),
С(4; 5).
Розв’язок. Студенту рекомендовано зробити Рис.. Очевидно, мно+
жину всіх внутрішніх точок трикутника АВС можна розглянути як
перетин трьох півплощин, з яких перша обмежена прямою АВ і
містить

150
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
точку С, друга обмежена прямою ВС і містить точку А, третя обме+
жена прямою АС і містить точку В.
Знайдемо нерівність, що визначає першу із цих півплощин. Скла+
демо рівняння прямої АВ, знаючи координати точок А і В:
21
62 31
xy
або х – 2у = 0.
Підставляючи в ліву частину цього рівняння координати точки
С, одержуємо 4 – 25 = –6 < 0. Отже, перша півплощина визначаєть+
ся нерівністю
х – 2у < 0.
Аналогічно, площина, що обмежена прямою ВС і містить точку
А, визначається нерівністю:
х + у – 9 < 0.
А площина, що обмежена прямою АС і містить точку В — не+
рівністю:
2х – у – 3 < 0.
Отже множина всіх внутрішніх точок трикутника АВС визна+
чається системою нерівностей
20,
90,
230.
xy
xy
xy
°
®
°
¯
Якщо замість строгих нерівностей (< або >) розглядати не строгі
нерівності (
d
або
t
), то в визначеній ними області включаються і
границі цих півплощин.
Наприклад область розв’язків нерівностей:
20,
90,
230.
xy
xy
xy
d
°
d
®
°
d
¯
є область, що обмежена трикутником АВС, включаючи як її
внутрішні, так і граничні точки, тобто і точки відрізків АВ, ВС, АС.
