Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

111
Розділ II. Аналітична геометрія
22
22
1
xy
ab
, (b
2
= c
2
– a
2
). (2.18)
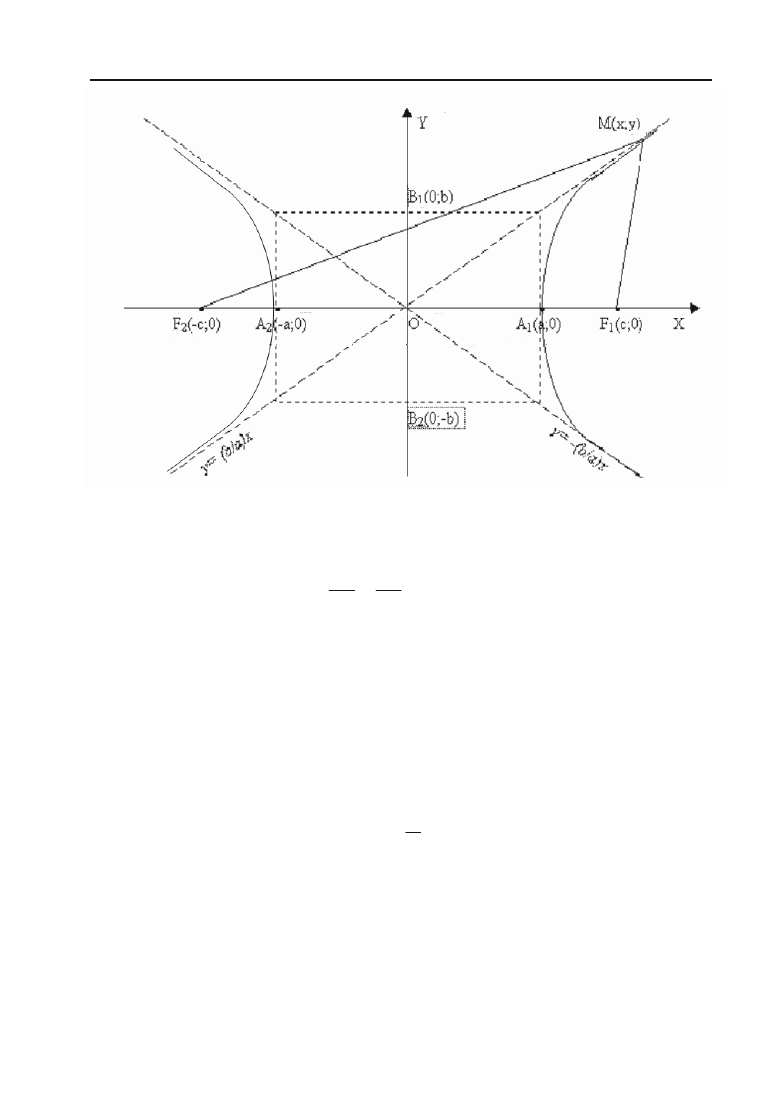
Координати фокусів гіперболи F
1
(c; 0) i F
2
(–c; 0). Відстань між
фокусами дорівнює 2с.
Точки перетину гіперболи з віссю абсцис А
1
(а; 0), А
2
(–а; 0) нази+
ваються дійсними вершинами. Відстань А
1
А
2
= 2а називається дійсною
віссю гіперболи.
Точки В
1
(0; b), B
2
(0; –b) називаються уявними вершинами, а
відрізок В
1
В
2
= 2b — уявною віссю гіперболи.
Ексцентриситет гіперболи
1
c
e
a
!
.
Відстані r
1
та r
2
точки М(х; у) гіперболи до його фокусів назива+
ються фокальними радіусами цієї точки і визначаються за форму+
лами:
r
1
= eх – а, r
2
= eх + а,
за умови, що точка М(х; у) лежить на правій вітці гіперболи.
Рис. 2.15.

112
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Дві прямі, які паралельні уявній осі гіперболи і знаходяться від неї
на відстані
a
e
називаються директрисами гіперболи. Їхні рівняння:
2
a
x
c
,
2
a
x
c
.
Прямі, які визначаються рівняннями:
b
y
x
a
,
b
y
x
a
,
називаються асимптотами гіперболи.
Дві гіперболи, що задані рівняннями:
22
22
1
xy
ab
;
22
22
1
xy
ab
,
називаються спряженими. Вони мають спільні асимптоти.
Якщо вісі гіперболи рівні, тобто а = b, то гіпербола називається
рівнобічною, або рівносторонньою. Її рівняння має вигляд:
х
2
– у
2
= а
2
.
Її асимптотами служать бісектриси координатних кутів.
Якщо за вісі координат прийняти асимптоти рівносторонньої
гіперболи, то її рівняння приймає вигляд:
ху = k, де
2
2
a
k
.
2.3.4. Парабола
Параболою називається геометричне місце точок рівновіддале+
них від заданої точки — фокуса та заданої прямої — директриси
(рис. 2.16).
Канонічне рівняння параболи має вигляд:
у
2
= 2рх, (2.19)
де р — відстань від фокуса до директриси. Вершина параболи знахо+
диться в початку координат, віссю симетрії є вісь абсцис.
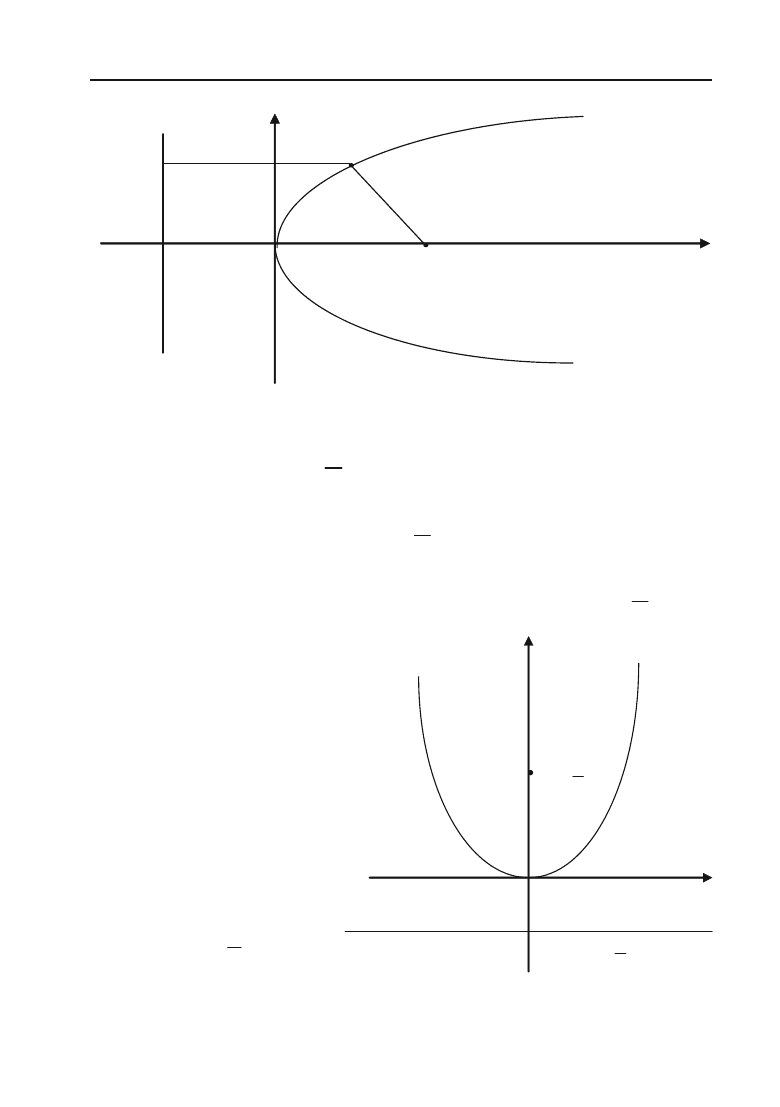
113
Розділ II. Аналітична геометрія
Координати фокуса F(
2
p
; 0). Рівняння директриси DN
має вигляд:
2
p
x
.
Фокальний радіус М(х; у) параболи дорівнює: r = х +
2
p
.
Ексцентриситет парабо+
ли вважається рівним оди+
ниці, e = 1.
Якщо віссю симетрії
параболи служить вісь ор+
динат (рис. 2.17), то рів+
няння параболи має виг+
ляд:
х
2
= 2qу. (2.20)
Рівняння директриси в
цьому випадку:
2
q
y
.
Рис. 2.16.
х = –p/2
D O F(p/2;0) Х
Y
M(x; y)
N
r
О Х
Y
F(0;
2
q
)
2
q
y
Рис. 2.17.

114
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.3.5. Приклади розв’язання задач
Задача 2.51. Скласти рівняння кола з центром в точці С(2; –3) і
радіусом, що дорівнює 6.
Розв’язок. В рівнянні (2.16) (х – а)
2
+ (у – b)
2
= r
2
маємо а = 2;
b = –3; r = 6. Зразу одержимо:
(х – 2)
2
+ (у + 3)
2
= 36.
Задача 2.52. Визначити центр і радіус кола, яке задано рівнянням:
х
2
+ у
2
– 2х + 4у – 20 = 0.
Розв’язок. Так як в заданому рівнянні коефіцієнт при х
2
і у
2
рівня
між собою і відсутній член з добутком координат, то задане рівнян+
ня є рівнянням кола. Його необхідно привести до вигляду (2.16).
Випишемо члени, які містять тільки х, і члени, які містять тільки у.
Виділимо повний квадрат:
х
2
– 2х = х
2
– 2х
1 + 1
2
– 1
2
= (х – 1)
2
– 1,
у
2
+ 4у = у
2
+ 2у
2 + 2
2
– 2
2
= (у + 2)
2
– 4.
Ліва частина заданого рівняння запишеться так:
22
22
(1)1(2)4200
24
xy
xx yy
звідки: (х – 1)
2
+ (у + 2)
2
= 25.
Порівнюючи одержане рівняння з рівнянням (2.16) приходимо
до висновку, що це рівняння визначає коло, центр якого має коорди+
нати С(1; –2), r
2
= 25, а r = 5.
Задача 2.53. Скласти рівняння кола, що проходить через точки
М
1
(–1; 1) і М
2
(1; –3), якщо центр його лежить на прямій 2х – у +1 = 0.
Рішення. Канонічне рівняння кола:
(х – а)
2
+ (у – b)
2
= r
2
.
Рівняння параболи з віссю симетрії, яка паралельна одній із ко+
ординатних осей, має вигляд:
(у – у
0
)
2
= 2р(х – х
0
),
або
(х – х
0
)
2
= 2q(у – у
0
),
де (х
0
; у
0
) — координати вершин параболи.

115
Розділ II. Аналітична геометрія
Так як коло проходить через точки М
1
(–1; 1) і М
2
(1; –3), то ко+
ординати цих точок повинні задовольняти рівнянню кола. Звідти
маємо два рівняння:
(–1 – а)
2
+ (1 – b)
2
= r
2
,
(1 – а)
2
+ (–3 – b)
2
= r
2
.
Якщо центр кола знаходиться на прямій 2х – у + 1 = 0, то коор+
динати центра повинні задовольняти рівнянню прямої. Одержуємо
трете рівняння:
2а – b + 1 = 0.
Розв’яжемо систему рівнянь:
222
222
(1 ) (1 ) ,
(1 ) ( 3 ) ,
210,
abr
abr
ab
°
®
°
¯
222
222
12 12 ,
12 96 ,
210.
aa bb r
aa bb r
ab
°
®
°
¯
Віднімемо від першого рівняння друге.
Одержимо систему:
4880,
210.
ab
ab
®
¯
Тепер віднімемо від першого рівняння друге, помножене на 2:
4880,
4220.
ab
ab
®
¯
Отримаємо:
–3b = 5,
5
3
b
.
Підставивши отримане значення b у рівняння 2a – b + 1 = 0,
одержимо значення параметру а:
5
1
14
3
223
b
a
.
Таким чином, координати центра кола знайдено: С
45
;
33
§·
¨¸
©¹
.

116
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Щоб визначити r
2
, скористаємося рівнянням:
r
2
= (–1 – а)
2
+ (1 – b)
2
;
r
2
= (–1 +
4
3
)
2
+ (1 +
5
3
)
2
=
16465
99 9
.
Отже, рівняння кола:
(х +
4
3
)
2
+ (у +
5
3
)
2
=
65
9
.
Задача 2.54. Скласти рівняння кола, що проходить через три
задані точки: М
1
(–1; 5), М
2
(–2; 2) і М
3
(5; 5).
Розв’язок. Шукане рівняння має вигляд: (х – а)
2
+ (у – b)
2
= r
2
.
Так як коло проходить через задані точки, то координати кожної з
цих точок задовольняють рівнянню кола.
Підставляємо по черзі в шукане рівняння координати заданих
точок, одержимо три рівняння для визначення а, b i r.
222
222
222
(1 ) (5 ) ,
(2 ) (2 ) ,
(5 ) (5 ) ,
abr
abr
abr
°
®
°
¯
222
222
222
1 2 25 10 ,
44 44 ,
25 10 25 10 .
aa bb r
aa bb r
aa bb r
°
®
°
¯
Від першого рівняння віднімемо друге, а потім від першого рівнян+
ня віднімемо трете. Одержуємо систему двох рівнянь з двома невідо+
мими:
214180,
24 12 0.
ab
a
®
¯
79,
2.
ab
a
®
¯
Звідки а = 2, b = 1.
Для знаходження r
2
скористаємося точкою М
1
(–1; 5) і рівнянням:
r
2
= (х – а)
2
+ (у – b)
2
.
r
2
= (–1 – 2)
2
+ (5 – 1)
2
= 9 + 16 = 25.
Шукане рівняння кола моє вигляд:
(х –2)
2
+ (у – 1)
2
= 25.
Задача 2.55. Знайти довжину осей, координати фокусів і екс+
центриситет еліпса 4х
2
+ 9у
2
= 144.
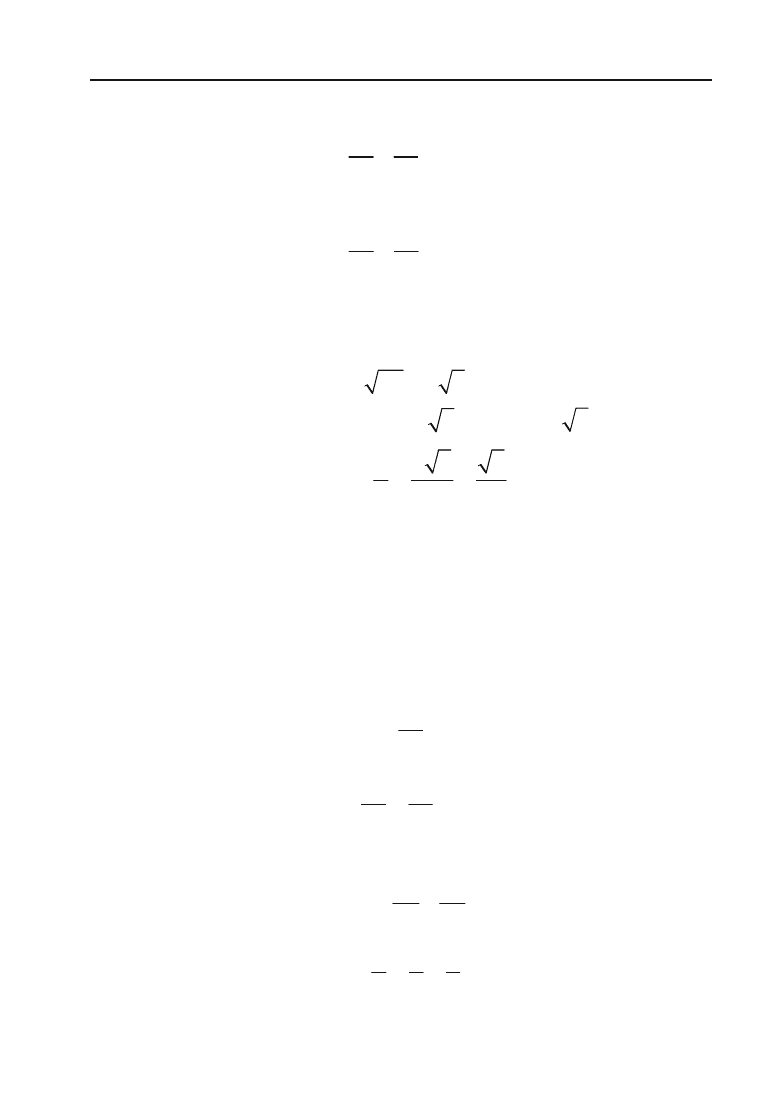
117
Розділ II. Аналітична геометрія
Розв’язок. Приведемо це рівняння до канонічного вигляду (2.17):
22
22
1
xy
ab
.
Розділивши обидві частини заданого рівняння на 144, одержимо:
22
1
36 16
xy
.
Звідти одержуємо, що а
2
= 36, b
2
= 16. Отже а = 6, 2а = 12; b = 4,
2b = 8. Знаючи а і b, із співвідношення а
2
– с
2
= b
2
знаходимо с:
с
2
= а
2
– b
2
= 36 – 16 = 20,
20 2 5c
.
Координати фокусів будуть: F
1
(
25
; 0) і F
2
(
25
; 0).
Ексцентриситет еліпса
25 5
63
c
a
H
.
Задача 2.56. Велика вісь еліпса дорівнює 8, а відстань між ди+
ректрисами дорівнює 16. Знайти рівняння еліпса. Чому дорівнює його
ексцентриситет?
Розв’язок. Для знаходження рівняння еліпса необхідно знайти його
піввісі а ти b. За умовою 2а = 8, а = 4.
Піввісь b знаходимо із співвідношення b
2
= а
2
– с
2
, а с можна
знайти, використовуючи відстань між директрисами
d
1
d
2
=
2
2
a
c
= 16,
22
4
2
88
a
c
.
Таким чином, b
2
= 4
2
– 2
2
= 16 – 4 = 12.
Одержуємо рівняння еліпса:
22
1
16 12
xy
.
Ексцентриситет еліпса
21
42
c
e
a
.
118
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Задача 2.57. Скласти рівняння гіперболи, фокуси якої знаходять+
ся на осі абсцис, симетрично відносно початку координат, якщо за+
дана точка М
1
(
9
2
; –1) гіперболи та рівняння асимптот
2
3
y
x r
.
Розв’язок. Для знаходження рівняння гіперболи
22
22
1
xy
ab
не+
обхідно знайти її піввісі а та b. Скористуємося умовою: точка
М
1
(
9
2
; –1) знаходиться на гіперболі, а це означає, що координати
точки М
1
повинні задовольняти рівнянню гіперболи:
2
2
22
9
(1)
2
1
ab
§·
¨¸
©¹
,
22
81 1
1
4
ab
.
Рівняння асимптот
b
y
x
a
r
, а ми маємо
2
3
y
x r
. Отже,
2
3
b
a
.
Одержали систему рівнянь:
22
22 2 2
81 1
1,
81 1 81 9
4
1, 1,
2
444
3
22
..
2
33
.
3
a
a
ab a a
ba ba
ba
°
§·
°°
°
°° °
¨¸
®® ®
©¹
°° °
°°
°
¯¯
°
¯
2
72
1,
4
2
.
3
a
ba
°
°
®
°
°
¯
2
18,
2
.
3
a
ba
°
®
°
¯
32,
2
.
3
a
ba
°
®
°
¯

119
Розділ II. Аналітична геометрія
Підставимо отримані значення параметрів в канонічне рівняння
гіперболи:
22
22
1
(3 2) (2 2)
xy
.
Таким чином, отримуємо шукане рівняння гіперболи:
22
1
18 8
xy
.
Задача 2.58. Знайти канонічне рівняння гіперболи, якщо кут між
її асимптотами дорівнює 120
о
і відстань між фокусами дорівнює
83
.
Розв’язок. Канонічне рівняння гіперболи має вигляд:
22
22
1
xy
ab
.
Рівняння асимптот
b
y
x
a
r
, де
tg
b
a
M
, а
M
– кут нахилу
асимптоти до осі Ох.
Так як кут між асимптотами дорівнює 120
о
, то
120
60
2
M
D
D
.
Звідси
tg60
b
a
D
;
3
b
a
;
3ba
.
За умовою задачі
283c
, то
43c
. Із співвідношення
с
2
= а
2
+ b
2
одержуємо друге рівняння:
(
43
)
2
= а
2
+ b
2
.
Розв’яжемо систему рівнянь:
22
48,
3.
ab
ba
°
®
°
¯
22
(3) 48,
3.
aa
ba
°
®
°
¯
22
2
2
1
6
(2 3)
xy
.
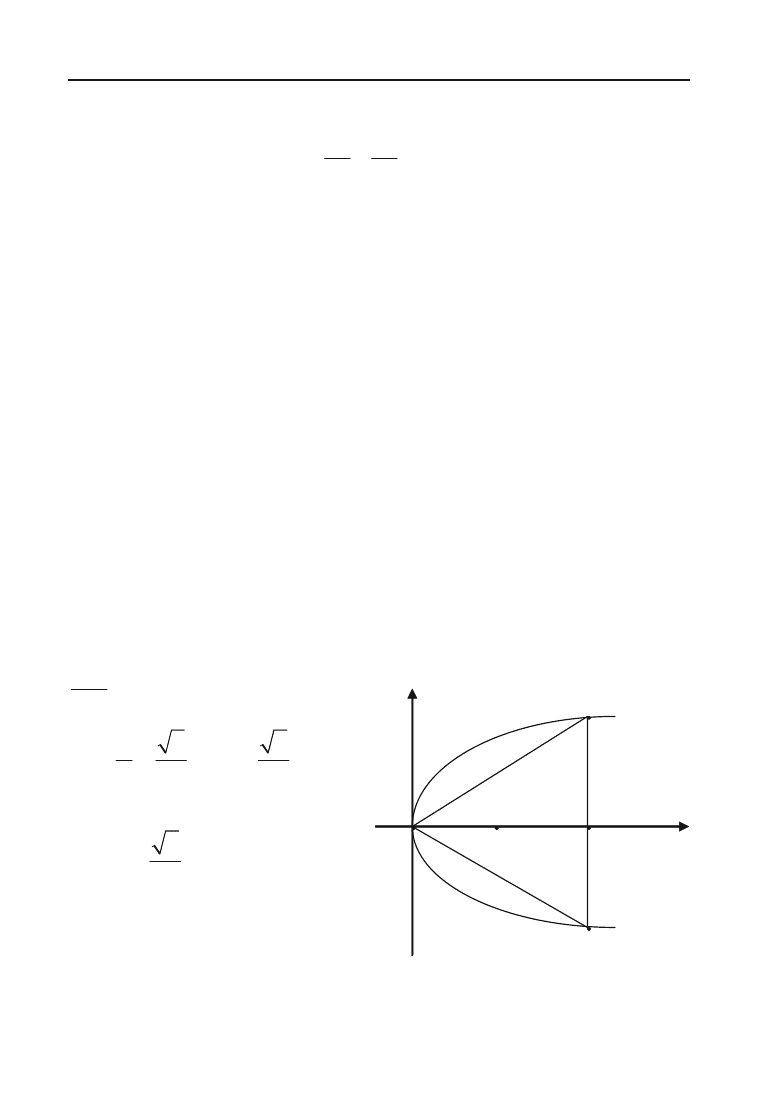
120
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Отримуємо рівняння:
22
1
12 36
xy
.
Задача 2.59. Скласти рівняння параболи, знаючи, що парабола
симетрична відносно осі Ох, проходить через точку М(1; –4) і поча+
ток координат.
Розв’язок. Канонічне рівняння параболи, що симетрична віднос+
но осі Ох, вершина якої знаходиться в початку координат є у
2
= 2рх.
Для складання рівняння необхідно знайти значення параметра р. Так
як парабола проходить через точку М(1; –4), то координати цієї точ+
ки задовольняють рівнянню параболи:
(–4)
2
= 2р
1, 16 = 2р, р = 8.
Звідси у
2
= 16х.
Задача 2.60. Обчислити довжину сторін правильного трикутни+
ка, який вписаний в параболу у
2
= 2рх.
Розв’язок. Трикутник АОВ розміщений симетрично відносно осі
параболи. Одна із його вершин співпадає з вершиною параболи, а
протилежна сторона — перпендикуляр до осі параболи (рис. 2.18).
За умовою задачі
A
OB+
рівносторонній. Кут
60
A
OB
D
, то
30AOD
D
. Нехай координати точки А(х; у). З
DOA+
маємо
tg30
AD
OD
D
, тобто:
33
,
33
y
y
x
x
.
Отже, точка А має координа+
ти А(х;
3
3
x
).
Ця точка лежить на пара+
болі, її координати задовольня+
ють рівнянню параболи. Звідти:
О F
Y
A
B
D
X
Рис. 2.18.
