Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

81
Розділ II. Аналітична геометрія
2.1.1. Відстань між двома точками
Якщо точки М
1
(x
1
; y
1
) та М
2
(x
1
; y
2
) належать двомірному просто+
ру R
2
, то відстань між двома точками визначається за формулою:
22
21 21
()()
dxx yy
. (2.1)
Якщо ж точки М
1
(x
1
; y
1
; z
1
) та М
2
(x
2
; y
2
; z
2
) належать трьохмірно+
му простору R
3
, то відстань між двома точками визначається за фор+
мулою:
222
21 21 21
()()()
dxx yy zz
. (2.2)
2.1.2. Поділ відрізка в заданому відношенні
Якщо точка М(x; y; z) поділяє відрізок, що визначений точками
М
1
(x
1
; y
1
; z
1
) та М
2
(x
2
; y
2
; z
2
) в відношенні
1
2
MM
MM
O
, то її координа+
ти знаходяться за формулами:
12 12 12
, ,
111
xx yy zz
x yz
OOO
OOO
. (2.3)
У випадку, якщо точка М поділяє відрізок М
1
М
2
навпіл, тоді l = 1,
і координати точки М визначаються за формулами:
12 12 12
, ,
222
xx yy zz
x yz
. (2.4)
Точки, що лежать на координатних площинах мають одну із ко+
ординат, яка дорівнює нулю.
Між трьома числами (x; y; z) і точками простору встановлена
взаємно однозначна відповідність
. Кожній трійці чисел відповідає
одна і тільки одна точка простору
і, навпаки, кожній точці простоA
ру відповідає одна трійка чисел (x; y; z)
.
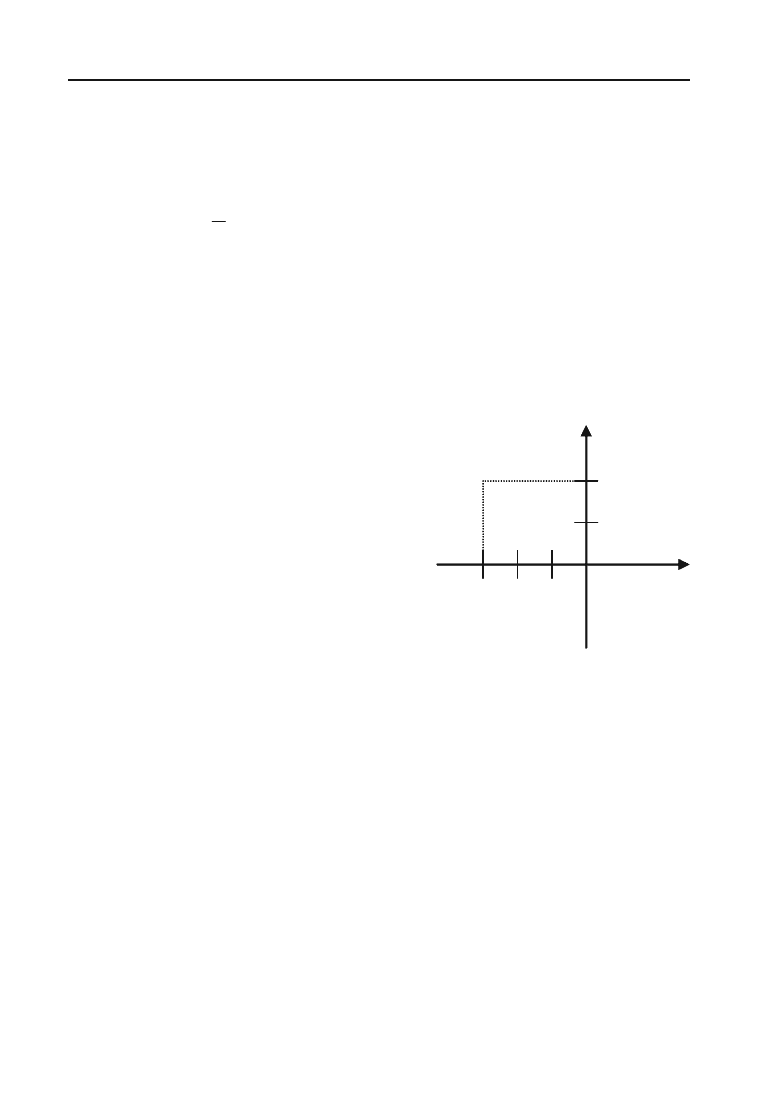
82
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
2.1.4. Приклади розв’язання задач
Задача 2.1. Побудувати точку С(–3; 2).
Розв’язок. Абсциса точки С дорів+
нює –3, а її ордината 2. Виберемо оди+
ницю масштабу та візьмемо на пло+
щині прямокутну систему координат.
Відкладаємо на осі Ох вліво від почат+
ку координат О відрізок, ОА, величи+
на якого дорівнює –3, а на осі Оy уго+
ру від початку координат — відрізок
ОВ, який дорівнює 2. Проводимо че+
рез точку А перпендикуляр до осі Ох,
а через точку В — перпендикуляр до
осі Оy. Перетин цих перпендикулярів
і визначить точку С (рис. 2.3).
Задача 2.2. Точка М(а; b) знаходиться у першому координат+
ному куті. Визначити координати точки N, яка симетрична точці М
відносно бісектриси цього координатного кута.
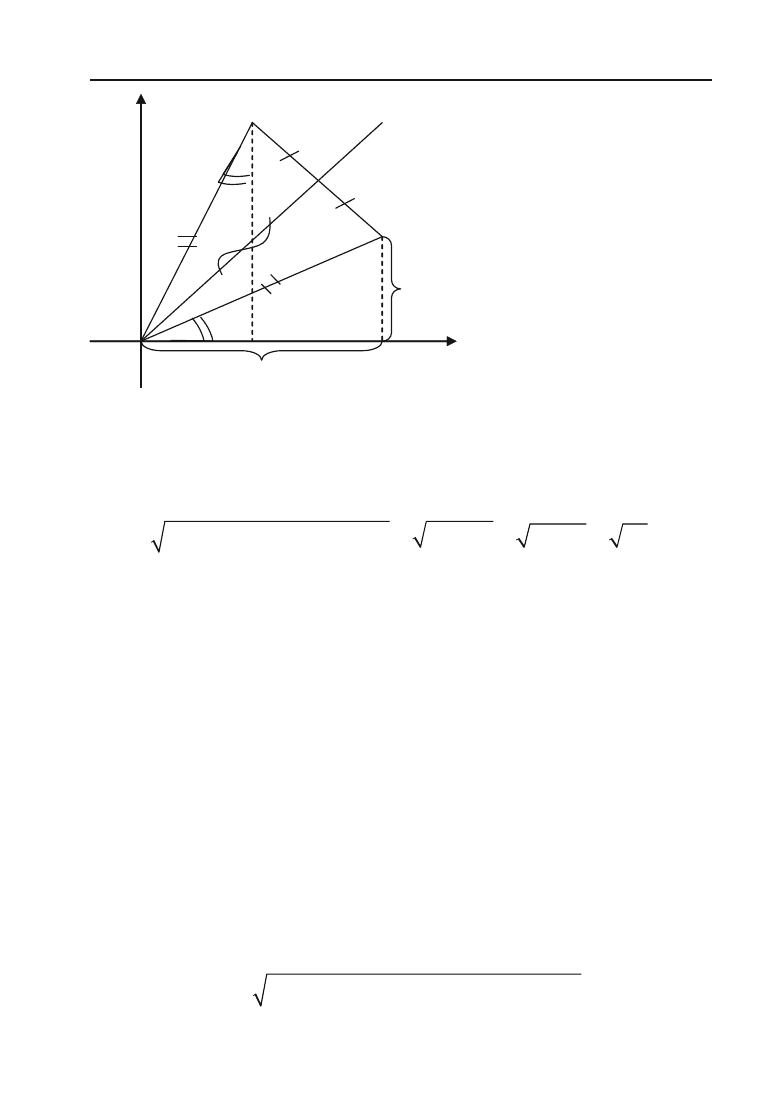
Розв’язок. Оскільки точка N симетрична точці М відносно бісект+
риси першого координатного кута, то вона лежить з точкою М на пер+
пендикулярі, який проведений до бісектриси ОР і МР = РN (рис. 2.4).
Враховуючи це, а також те, що в трикутниках OMP i OPN катет
ОР – спільний, маємо, що ці прямокутні трикутники рівні між со+
бою. Розглянемо тепер трикутники ONE i OMD. Прийдемо до вис+
новку, що вони рівні, cкільки будучи прямокутними вони мають рівні
гіпотенузи і рівні гострі кути MOD i ONE.
2.1.3. Площа трикутника
Площа трикутника за відомими координатами його вершин
A(x
1
; y
1
), B(x
2
; y
2
), C(x
3
; y
3
) обчислюється за формулою:
1223 2313
1
(( )( ) ( )( ))
2
Sxx
yy
xx
yy
. (2.5)
Одержане за допомогою цієї формули число необхідно взяти по
абсолютній величині.
Рис. 2.3.
О
–3
2
y
x
А
В
С
83
Розділ II. Аналітична геометрія
Із рівності трикут+
ників ONE i OMD маємо,
що OD = NE, а MD = OE.
Так як за умовою абсци+
са OD точки М дорівнює
а, а її ордината MD = b то
ми приходимо до виснов+
ку, що точка N має абсци+
су OE = MD = b, а орди+
нату NE = OD = a.
Отже, координатами
точки N служать числа b
та a: N(b; a).
Задача 2.3. Знайти відстань між точками M
1
(4; –5) і M
2
(7; –1).
Розв’язок. За формулою (2.1) для відстані d між двома точками,
якщо взяти в ній x
1
= 4; x
2
= 7; y
1
= –5; y
2
= –1, одержуємо:
2222
(7 4) ( 1 ( 5)) 3 4 9 16 25 5
d
.
Задача 2.4. Задана точка Р(3; 5; 2). Знайти координати точки,
що симетрична з точкою Р:
1) відносно початку координат;
2) відносно площини xOz;
3) відносно осі Oy.
Розв’язок.
1) Точка Р лежить в І октанті, симетрична їй точка відносно по+
чатку координат Р
1
буде знаходитися в VII октанті. Її координати –
Р
1
(–3; –5; –2).
2) Точка Р
2
, симетрична точці Р відносно площини xOz, буде зна+
ходитися в IV октанті, отже, її координата Р
2
(3; –5; 2).
3) Точка Р
3
, симетрична точці Р відносно осі Oy, буде знаходити+
ся в VІ октанті, отже, її координати Р
3
(–3; 5; –2).
Задача 2.5. Показати, що один із внутрішніх кутів трикутника
А(3; 5; 3), В((2; –1; 4), С(0; –2; 1) тупий.
Розв’язок. Знайдемо довжини сторін трикутника за формулою (2.2):
222
21 21 21
()()()
dxx yy zz
.
Oa DX
E
M
P
N
b
Y
Рис. 2.4.
84
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
АВ =
222
(2 3) ( 1 5) (3 4) 1 36 1 38
;
АС =
222
(0 3) ( 2 5) (1 3) 9 49 4 62
;
ВС =
222
(
02
)(
21
)(
14
)
419 14
.
Розглянемо співвідношення між числами, що виражають квадра+
ти сторін даного трикутника:
38 + 14 = 52, 62 > 52, 62 > 38 + 14,
тобто
АС
2
> AB
2
+ BC
2
.
Отже, сторона АС лежить проти тупого кута. Кут В – тупий.
Задача 2.6. На осі Oz знайти точку, рівновіддалену від двох то+
чок М(–2; 1; 4) і N(3; 0; 1).
Розв’язок. Точка, що лежить на осі Oz має координати Р(0; 0; z).
Знайдемо відстані МР і NP:
22 2 2
22
(0 2) (0 1) ( 4) 4 1 ( 4)
5816 821;
MP z z
zz zz
222 2
22
(0 3) (0 0) ( 1) 9 0 ( 1)
921 210.
NP z z
zz zz
Згідно умови, що MP = PN, одержуємо:
22
821 210
zz zz
.
Розв’язавши одержане рівняння, знаходимо аплікату точки Р:
z
2
–
8z + 21 = z
2
–2z + 10;
–6z = –11;
z = 11/6.
Р(0; 0; 11/6).
Задача 2.7. Знайти координати кінця В відрізка, якщо один
кінець відрізка — точка А(–5; –7), а середина відрізка — С(–9; –12).
Розв’язок. В формулах (2.4)
12 12
,
22
xx
yy
xy
,

85
Розділ II. Аналітична геометрія
координати середини відрізка позначено через x i y. За умовою за+
дачі x = –9; y = –12.
Координати одного кінця відрізка точки А в цих формулах: x
1
= –5;
y
1
= –7. Координати відрізка точки В (другого кінця відрізка) — ве+
личини невідомі, позначені через x
2
i y
2
.
Тоді за формулою (2.4) для визначення цих невідомих одержує+
мо два рівняння:
–9 =
2
5
2
x
; –12 =
2
7
2
y
.
Звідси:
–18 = –5 + x
2
i x
2
= –13;
–24 = –7 + y
2
i y
2
= –17.
В(–13; –17).
Задача 2.8. Відрізок М
1
М
2
, що з’єднує точки М
1
(2; 5) і М
2
(4; 9),
розділити в відношенні l = 1/3.
Розв’язок. Умова задачі вимагає знайти координати точки Р, що
ділить відрізок М
1
М
2
у відношенні l = 1/3.
Використовуючи формули (2.3), точку М
1
(2; 5) будемо вважати
початком відрізка, а точку М
2
(4; 9) — його кінцем. Тоді x i y — коор+
динати точки Р, які ми шукаємо, x
1
i y
1
– координати точки М
1
, x
2
i
y
2
— координати точки М
2
; l = 1/3. Отже, у нас x
1
= 2; x
2
= 4; y
1
= 5;
y
2
= 9. Маємо за формулами:
1
24
3
1
1
3
x
4
2
3
4
3
x
5
2
x
;
1
29
3
1
1
3
y
53
4
3
y
6
y
.
Точка Р має координати Р(5/2; 6).
Задача 2.9. Визначити координати кінця відрізка АВ, якщо відо+
мо, що його початок в точці А(–1; 2; 4) і точка М(2; 0; 2) відтинає від
нього третю частину.

86
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розв’язок. Точка М відтинає від відрізка АВ третю частину його
довжини, ділить його в відношенні l =
1
2
AM
MB
.
Використаємо формули поділу відрізка в заданому відношенні (2.3):
1
A
B
M
xx
x
O
O
,
1
A
B
M
y
y
y
O
O
,
1
A
B
M
zz
z
O
O
.
Підставивши в ці формули координати точок А і М:
1
1
2
2
1
1
2
B
x
;
1
2
2
0
1
1
2
B
y
;
1
4
2
2
1
1
2
B
z
,
та розв’язавши одержані рівняння, знайдемо:
311
2 1 , 4; 8
222
BB B
xx x
;
21 1
0 2 ; 2; 4
32 2
BB B
yy y
;
311
2 4 ; 1; 2.
222
BB B
zz z
В(8; –4; –2).
Задача 2.10. Задано дві вершини трикутника: А(–3; –2; 2),
В(4; 1; –2). Знайти третю вершину С, знаючи, що середина сторони
АС лежить на осі Oy, а середина сторони ВС — на площині xOz.
Розв’язок. Позначимо середину сторони АС буквою М. Так як вона
лежить на осі Oy, то її координати М(0; y
M
; 0). Середину сторони ВС
позначимо як N, яка лежить на площині xOz, N(x
N
; 0; z
N
). Скористав+
шись формулами поділу відрізка навпіл, одержимо:
2
A
C
M
xx
x
;
3
0
2
C
x
; х
с
= 3;
2
A
C
M
zz
z
;
2
0
2
C
z
; z
c
= –2;

87
Розділ II. Аналітична геометрія
2.1.5. Задачі для самостійного розв’язку
2.11. Встановити, які координати має точка симетрична точці
(–3; 5):
a) відносно осі Ох;
b) відносно осі Oy;
c) відносно початку координат;
d) відносно бісектриси І та ІІІ координатних кутів;
e) відносно бісектриси ІІ та IV координатних кутів.
2.12. На якій відстані від початку координат знаходяться точки:
M(3; 4), N(12; –5); P(7; –24); Q(–6; –8)?
2.13. Знайдіть периметр трикутника, якщо координати його вер+
шин А(–3; –6); В(4; –1); С(5; –2).
2.14. Визначити вид трикутника якщо координати його вершин
А(2; –5); В(–7; –4); С(–1; 6).
2.15. Точка, рухаючись рівномірно та прямолінійно, за 4 сек пе+
ремістилась із положення А(6; –7) в положення В(–4; 5). Де знахо+
дилась точка в момент часу 2 сек?
2.16. На осі ординат знайти точку, рівновіддалену від точок
М
1
(1; –3; 7) і М
2
(5; 7; –5).
2.17. Задано три послідовні вершини паралелограма: А(1; 1);
В(2; 2); С(3; –1). Знайти його четверту вершину D.
2.18. Задано дві вершини А(2; –3; –5), В(–1; 3; 2) паралелограма
ABCD і точка перетину його діагоналей М(4; –1; 7). Визначити коор+
динати двох інших вершин цього паралелограма.
2.19. Задано вершини трикутника А(3; 2; –1); В(5; –4; 7) і
С(–1; 1; 2). Обчислити довжину його медіани, що проведена із вер+
шини С.
2.20. Задано вершини трикутника А(1; –1; –3), В(2; –1; 3),
С(–4; 7; 5). Обчислити довжину бісектриси його внутрішнього кута
при вершині В.
1
; 0
22
BC C
N
y
yy
y
; y
c
= –1.
С(3; –1; 2).

88
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§2.2. Пряма лінія на площині
В прямокутній системі координат рівняння прямої на площині
задається одним із наступних видів.
1. Рівняння прямої з кутовим коефіцієнтом:
y = kx + b, (2.6)
де k — кутовий коефіцієнт прямої, тобто тангенс того кута, який
пряма утворює з додатним напрямом осі Ох, причому, цей кут відра+
ховується від осі Ох до прямої проти годинникової стрілки; b — ве+
личина відрізка, що відтинає пряма на осі ординат. При b = 0 рівнян+
ня (2.6) має вигляд y = kx, і відповідна йому пряма проходить через
початок координат.
Рівняння прямої з кутовим коефіцієнтом розв’язане відносно
поточної координати у.
2. Загальне рівняння прямої
Ах + Ву + С = 0. (2.7)
Окремі випадки загального рівняння прямої:
а) якщо С = 0, то рівняння (2.7) буде мати вигляд:
Ах + Ву = 0,
A
y
x
B
,
якщо
A
k
B
, то y = kx, і пряма, що визначається цим рівнянням,
проходить через початок координат, так, як координати початку ко+
ординат х = 0, у = 0 задовольняють цьому рівнянню.
б) якщо в загальному рівнянні (2.7) В = 0, то рівняння матиме
вигляд:
Ах + С = 0, або х =
A
C
= а.
Рівняння не містить змінної у, і цим рівнянням визначається
пряма, яка паралельна осі Оу.
в) якщо в загальному рівнянні (2.7) А = 0, то рівняння приймає
вигляд:
Ву + С = 0, або у =
B
C
= b.

89
Розділ II. Аналітична геометрія
Рівняння не містить змінної х, і цим рівнянням визначається
пряма, яка паралельна осі Ох.
Необхідно запам’ятати, якщо пряма паралельна якій+небудь ко+
ординатній вісі, то в її рівнянні відсутній член, який містить коорди+
нату, однойменну з цією віссю.
г) При С = 0 і А = 0 — рівняння (2.7) має вигляд Ву = 0 або у = 0.
Це рівняння вісі Ох.
д) При С = 0 і В = 0 рівняння (2.7) запишеться в вигляді Ах = 0
або х = 0. Це рівняння вісі Оу.
3. Рівняння прямої в відрізках на осях:
1
xy
ab
, (2.8)
де а — величина відрізку, який відтинає пряма на вісі Ох;
b — величина відрізку, який відтинає пряма на вісі Оу.
Кожний з цих відрізків відкладається від початку координат.
4. Якщо пряма має кутовий коефіцієнт k і проходить через зада+
ну точку М
0
(х
0
; у
0
), то її рівняння має вигляд:
у – у
0
= k (x – x
0
). (2.9)
Якщо в цьому рівнянні параметру k надавати різні значення, то
будемо одержувати різні прямі, які проходять через задану точку
(х
0
; у
0
). Тоді рівняння (2.9) дає пучок (в’язку) прямих з центром в
точці М
0
(х
0
; у
0
).
5. Якщо пряма проходить через дві задані точки М
1
(х
1
; у
1
) і
М
2
(х
2
; у
2
), то рівняння:
11
221
1
xx
yy
xx
yy
, (2.10)
називається рівнянням прямої, що проходить через дві задані точки
М
1
(х
1
; у
1
) і М
2
(х
2
; у
2
).
6. Якщо задано вектор
_
S
= {m; n}, паралельний прямій, і точку
М
0
(х
0
; у
0
) на цій прямій, то рівняння прямої можна записати у виг+
ляді:
00
xx
yy
mn
.
90
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Вектор
_
S
називається напрямним вектором прямої.
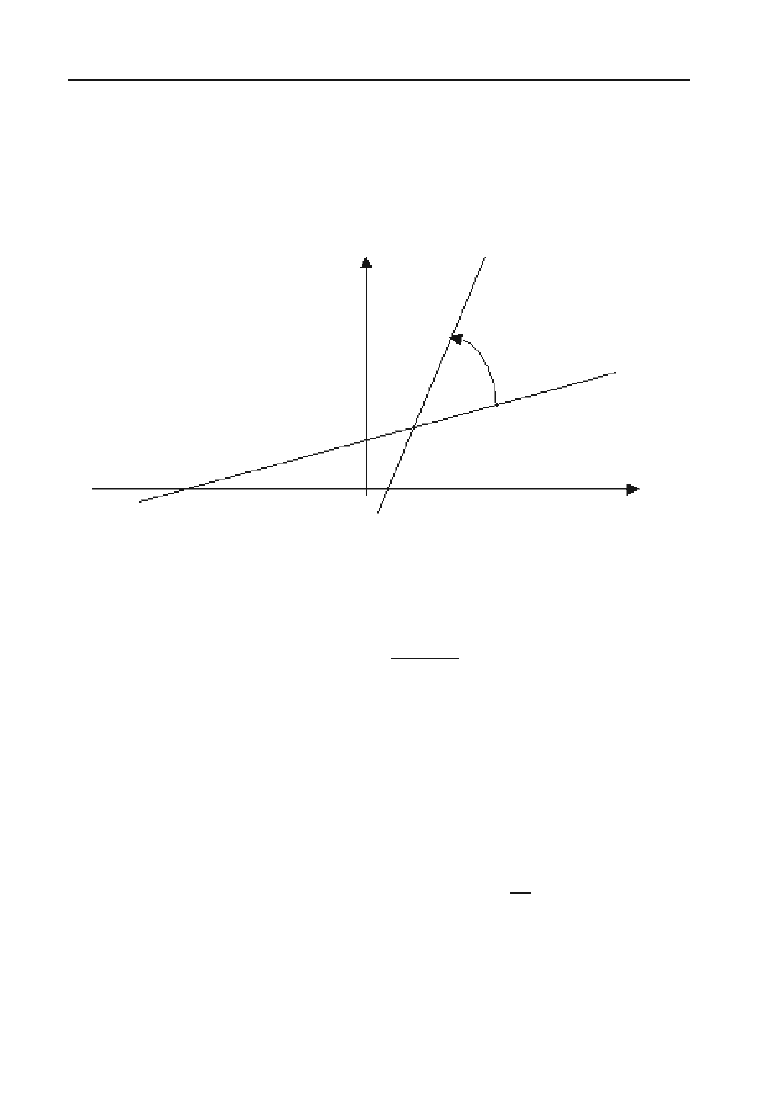
7. Кутом між прямими у = k
1
x + b
1
і y = k
2
x + b
2
називається кут,
на який необхідно повернути пряму (з кутовим коефіцієнтом k
1
) до
збігу її з другою прямою (з кутовим коефіцієнтом k
2
), проти годин+
никової стрілки.
Рис. 2.5.
І цей кут
M
обчислюється за формулою:
21
12
tg
1
kk
kk
M
. (2.11)
Необхідно звернути увагу на те, що в чисельнику дробу від куто+
вого коефіцієнта другої прямої віднімається кутовий коефіцієнт пер+
шої прямої.
Умова паралельності двох прямих:
k
1
= k
2
.
(2.12)
Умова перпендикулярності двох прямих:
k
1
k
2
= –1, або
2
1
1
k
k
. (2.13)
Якщо прямі задані рівняннями в загальному вигляді:
А
1
х + В
1
у + С
1
= 0 і А
2
х + В
2
у + С
2
= 0,
О X
Y
M
у
=
k
1
x
+
b
1
у
=
k
2
x
+
b
2
