Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

421
Розділ VI. Інтегральне числення
3
3
22
1
(1)
4
xdx
xx
³
=
3
3
22
6
((2sin ) 1)2cos
(2sin ) 4 (2sin )
ttdt
tt
S
S
³
=
3
3
2
6
(8sin 1)
4sin
tdt
t
S
S
³
=
= 2
3
6
sin
tdt
S
S
³
+
1
4
3
2
6
sin
dt
t
S
S
³
= –2cos t
3
6
S
S
–
1
4
ctg t
3
6
S
S
=
= –2(cos
3
S
– cos
6
S
) –
1
4
(ctg
3
S
– ctg
6
S
) = –2(
1
2
–
3
2
) –
–
1
4
(
3
3
–
3
) =
7
23
– 1.
Приклад 6.202. Обчислити
10
0
(3)sin5
x
xdx
S
³
.
Розв’язок. Для обчислення даного інтеграла використаємо фор+
мулу інтегрування частинами:
b
a
udv
³
= uv
b
a
–
b
a
vdu
³
.
(3), sin5
1
,sin5 cos5
5
ux dv xdx
du dx v xdx x
³
10
0
(3)sin5
x
xdx
S
³
= –
1
5
(x + 3)cos5x
2
0
S
+
1
5
10
0
(3)sin5
x
xdx
S
³
=
= –
1
5
(
10
S
+ 3)cos 5
10
S
+
1
5
(0 + 3)cos 5
0 +
1
25
sin 5x
2
0
S
=
422
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
=
1
5
(
30
10
S
)cos
2
S
+
3
5
cos 0 +
1
25
sin 5
10
S
–
1
25
sin 5
0 =
=
1
5
(
30
10
S
)0 +
3
5
1 +
1
25
1 –
1
25
0 =
3
5
+
1
25
=
16
25
= 0,64.
Приклад 6.203. Обчислити
1
0
arcsin
x
dx
³
.
Розв’язок.
2
arcsin ,
1
,
1
u x dv dx
du dx v x
x
1
0
arcsin
x
dx
³
= xarcsin x
1
0
–
1
2
0
1
xdx
x
³
= 1
arcsin 1 –
– 0
arcsin 0 +
2
1
x
1
0
=
2
S
– 1.
Приклад 6.204. Обчислити
1
0
arctg
xxdx
³
.
Розв’язок.
2
2
arcctg ,
,
2
1
uxdvxdx
dx x
du v xdx
x
³
Застосовуючи до заданого інтеграла формулу інтегрування час+
тинами, одержимо:
1
0
arctgxxdx
³
=
2
2
x
arctg x
1
0
–
1
2
2
0
2
1
xdx
x
³
=
1
2
4
S
–
1
2
1
2
2
0
11
1
x
dx
x
³
=
423
Розділ VI. Інтегральне числення
=
8
S
–
1
2
(
1
0
dx
³
–
1
2
0
1
dx
x
³
) =
8
S
–
1
2
(x
1
0
– arctg x
1
0
) =
8
S
–
1
2
(1 – 0 –
– arctg 1 + arctg 0) =
8
S
–
1
2
(1 –
4
S
) =
8
S
–
1
2
+
8
S
=
4
S
–
1
2
=
2
4
S
.
Приклад 6.205. Обчислити
2
1
ln
e
xdx
³
.
Розв’язок. Нехай
2
ln ,
1
2ln ,
u x dv dx
du x dx v x
x
2
1
ln
e
x
dx
³
= xln
2
x
1
e
–
1
1
2ln
e
x
xdx
x
³
= eln
2
e – 1ln
2
1 – 2
1
ln
e
x
dx
³
=
= e – 2
1
ln
e
xdx
³
=
ln ,
1
,
uxdvdx
du dx v x
x
= e – 2
1
ln
e
xdx
³
= e – 2(xln x
1
e
–
1
1
e
xdx
x
³
) = e – 2(eln e – 1ln 1 –
– x
1
e
) = e – 2e + 2e – 2 = e – 2.
Пригадаємо, що ln 1 = 0, ln e = 1.
424
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.7.2. Приклади для самостійного розв’язку
6.206.
5
0
13
xdx
x
³
. 6.207.
9
4
1
x
dx
x
³
.
6.208.
4
0
121
dx
x
³
. 6.209.
5
1
45
xdx
x
³
.
6.210.
ln 5
0
1
3
xx
x
ee
dx
e
³
. 6.211.
2
0
1sin cos
dx
x
x
S
³
.
6.212.
0
3
1
11
dx
x
³
. 6.213. cos
a
a
x
x
dx
a
³
.
6.214.
2
5
1
ln
x
dx
x
³
. 6.215.
4
2
0
tg
x
xdx
S
³
.
6.216.
2
1
ln( 1)
xx dx
³
. 6.217.
2
2
1
ln
e
x
dx
x
³
.
6.218.
1
2
0
x
³
e
–2x
dx. 6.219.
2
2
0
(1)sin2
x
xdx
S
³
.
6.220.
3
22
1
1
dx
xx
³
. 6.221.
2
2
2
1
4 x
dx
x
³
.
6.222.
1
2
0
ln(1 )
xxdx
³
.
425
Розділ VI. Інтегральне числення
§6.8. Геометричні застосування визначенних інтегралів
6.8.1.Обчислення площ плоских фігур
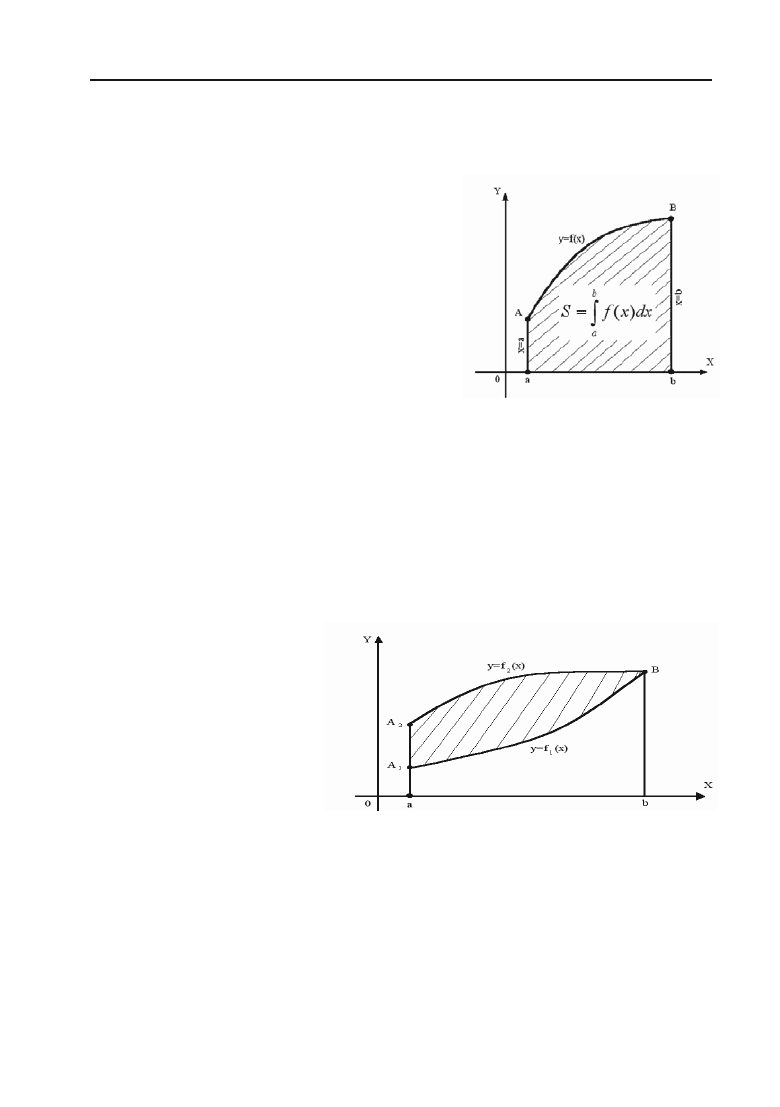
Площа плоскої фігури (рис. 6.1), що
обмежена неперервною кривою, рів+
няння якої в прямокутних координатах
має вигляд y = f(x), віссю Ox та двома
прямими x = a, x = b, (a < b), знахо+
диться за формулою:
()
b
a
Sfxdx
³
. (6.31)
Якщо функція f(x) скінчене число
раз змінює знак на відрізку [a; b], то відрізок [a; b], необхідно розді+
лити на частини, в кожній із яких функція зберігає один і той же
знак. При знаходжені площі фігури, що обмежена такою неперерв+
ною кривою, необхідно дотримуватись такого правила знаків: площі,
що знаходяться над віссю Ox, беруться зі знаком плюс, а площі, що
розміщені під віссю Ox, зі знаком мінус або обчислити інтеграл від
абсолютного значення функції.
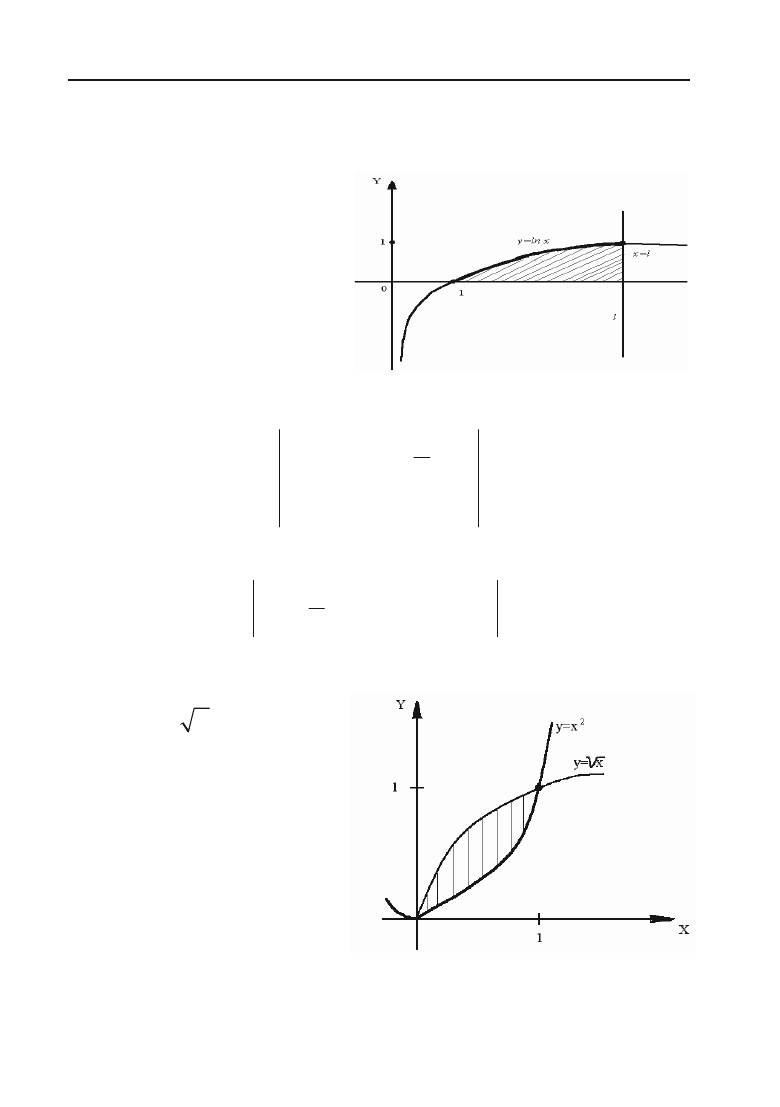
Якщо плоска фігура
обмежена двома непе+
рервними кривими, рів+
няння яких у прямокут+
них координатах y = f
1
(x)
і y = f
2
(x), причому
скрізь на відрізку [a; b],
f
2
(x)
t
f
1
(x), та двома
прямими x = a та x = b
(рис. 6.2), то площа виз+
начається за формулою:
21
() ()
b
a
Sfxfxdx
³
. (6.32)
Рис. 6.1.
Рис. 6.2.
426
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.8.1.1. Приклади розв’язання задач
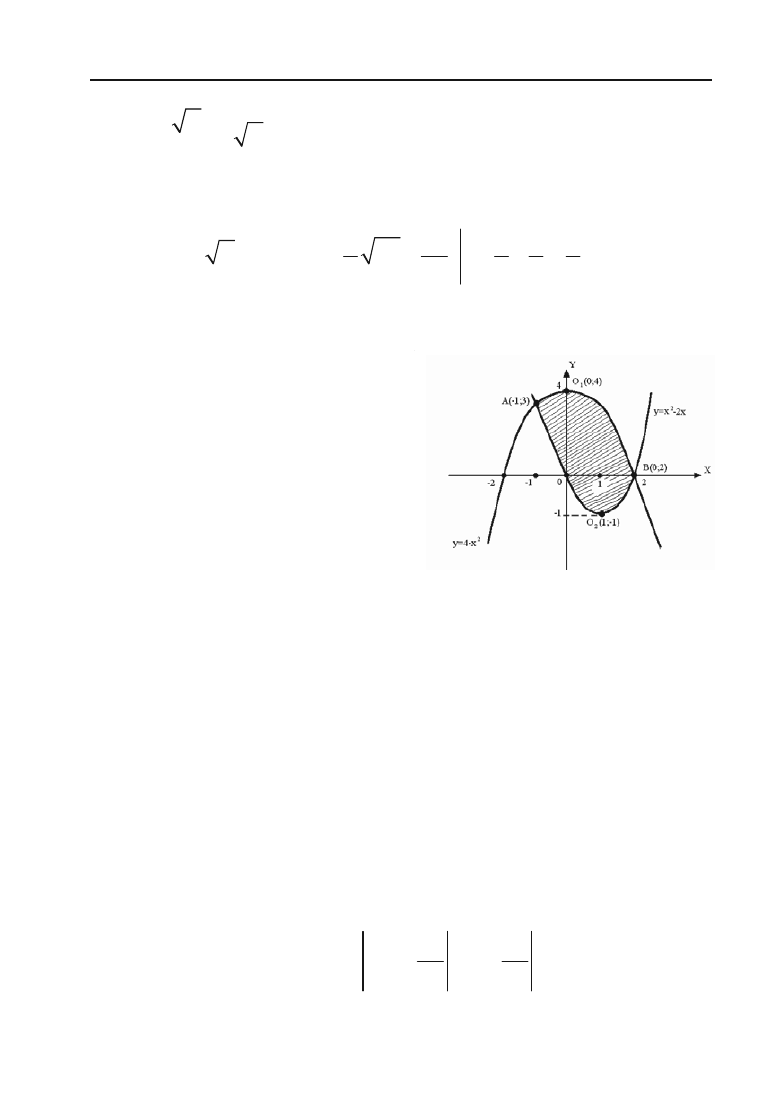
Задача 6.223.
Обчислити площу фігури, що обмежена лініями
y = ln x, x = l та віссю Ox.
Розв’язок. Побудуємо фі+
гуру. Межі інтегрування бачи+
мо із рис. 6.3: 1
d
x
d
l.
Використовуємо формулу
6.31, знаходимо площу фігури
1
ln
l
Sxdx
³
.
Інтегруємо частинами:
1
ln ,
,
uxdudx
x
dv dx V dx x
³
Отримали:
11
1
ln ln ln 1ln1 1 1
11
ll
ll
Sxdxxxxdxll xll
x
³³
(кв.од.)
Задача 6.224. Обчислити
площу фігури, що обмежена
лініями y =
x
і y = x
2
.
Розв’язок. Спочатку зобра+
зимо фігуру, площу якої по+
трібно знайти (рис. 6.4).
Знайдемо межі інтегру+
вання. Для цього необхідно
знайти точки перетину цих
парабол. Координати точок
перетину задовольняють
обом рівнянням, тому треба
розв’язати систему рівнянь
Рис. 6.3.
Рис. 6.4.
427
Розділ VI. Інтегральне числення
233
2
0
yx
xx xx x x
yx
°
®
°
¯
x
1
= 0, x
2
= 1.
Отже, 0
d
x
d
1, а площа фігури буде:
1
3
23
0
1
0
2211
()( )
33333
x
Sxxdx x
³
(кв.од.).
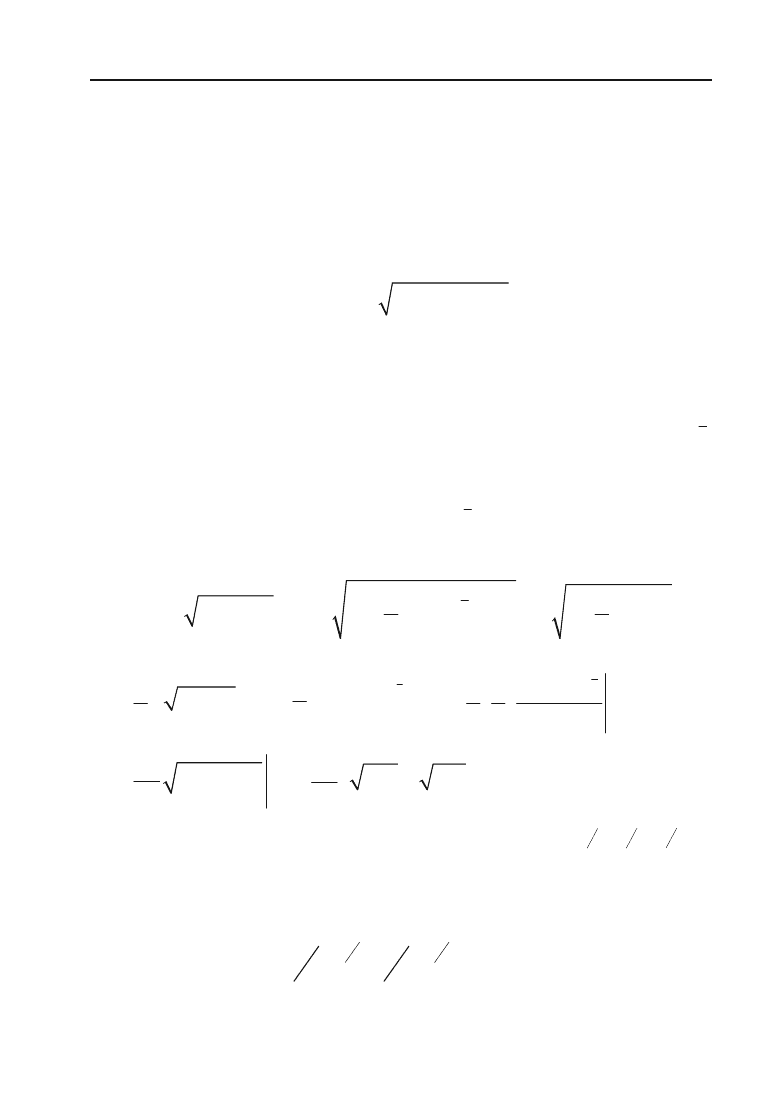
Задача 6.225. Обчислити площу фігури, що обмежена лініями
y = 4 – x
2
і y = x
2
– 2x.
Розв’язок. Побудуємо фігуру,
площу якої необхідно обчислити:
а) y = 4 – x
2
— є парабола, вер+
шина якої знаходиться в точці
O
1
(0; 4). Парабола перетинає вісь
Ox у точках (2; 0) і (–2; 0), а вісь
Oy у точці (0; 4).
б) y = x
2
– 2x — є парабола, вер+
шина якої знаходиться у точці
O
2
(1; –1). Парабола перетинає вісь
Ox у точках (0; 0) і (2; 0), а вісь Oy
у точці O(0; 0).
в) Визначимо точки перетину парабол. Розв’яжемо систему
рівнянь:
2
2
4
2
y
x
y
xx
°
®
°
¯
4 – x
2
= x
2
– 2x
2x
2
– 2x – 4 = 0, x
2
– x – 2 = 0.
Межі інтегрування: –1
d
x
d
2.
г) Визначимо площу фігури, використовуючи формулу 6.32.
222
22 2
111
(4 ) ( 2 ) (4 2 2 ) 4S x x x dx x x dx dx
³³³
–
22
2
11
22xdx xdx
³³
32
222
111
42 2 424(1)
32
xx
x
Рис. 6.5.

428
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.8.2. Обчислення довжини дуги кривої
1) Довжина дуги плоскої кривої, що визначена у прямокутних
координатах рівнянням y = f(x), знаходиться за формулою:
2
1(())
b
a
lfxdx
c
³
, (6.33)
де а і b — відповідно абсциси початку і кінця дуги.
6.8.1.2. Задачі для самостійного розв’язку
Обчислити площу фігур, що обмежені лініями. Зробити малюнки.
6.226. Параболою 4y = 8x – x
2
і прямою 4y = x + 6.
6.227. Параболою y = x
2
– 2 і прямою y = x.
6.228. Параболою y = 2x
2
з прямими x = 1 і x = 2 та віссю Ох.
6.229. Параболою y = 2x
2
+ 3x – 9 та віссю Ox.
6.230. Прямою x = 4, параболою y = 3x
2
– 6x і віссю Ox на
відрізку [0; 4].
6.231. Параболою y = (x + 2)
2
, прямою y = 4 – x та віссю Ox.
6.232. Гіперболою xy = 3 і прямою x + y = 4.
6.233. Параболами x
2
– 3y = 4 і x
2
+ y = 8.
6.234. Параболою y = 5x – 2x
2
та прямою y = 2x – 2.
6.235. Параболами x = 4 – y
2
і x = y
2
– 2y.
6.236. Параболами x = 8 – y
2
і x = y
2
.
6.237. Кривими
2
8
4
y
x
і
2
4
x
y
.
6.238. Параболою x = 2y
2
+ 6y і прямою x – y + 2 = 0.
6.239. Параболами y
2
– 2x = 2 і y
2
+ 2x = 6.
6.240. Параболами y = (x – 1)
2
і y
2
= x – 1.
3322
22
2(1)2(1)
33
16 2
84 419
33
(кв. од).
429
Розділ VI. Інтегральне числення
2) Якщо крива задана параметричними рівняннями:
()
()
x
t
y
t
M
W
½
¾
¿
,
причому
t
DE
dd
, а функції
()
t
M
і
()
t
W
мають неперервні похідні,
то довжина дуги:
22
() ()
tt
lx
y
dt
E
D
cc
³
. (6.34)
6.8.2.1. Приклади розв’язання задач
Задача 6.241.
Обчислити довжину дуги параболи
3
2
(1)yx
між точками A(2; –1) та B(5; –8).
Розв’язок. Знайдемо
1
2
3/2( 1)yx
c
. Підставимо в формулу
(6.33) і отримаємо:
55
1
22
2
22
39
1
()
1
((
1
))
1
(
1
)
24
B
A
X
AB
X
l
y
dx x dx x dx
c
³³ ³
=
=
5
2
1
95
2
xdx
³
=
1
2
5
2
1
(9 5)
2
xdx
³
=
3
2
5
2
11(9 5)
29 3/2
x
=
=
3
5
2
1
(9 5)
27
x
=
33
1
(40 13)
27
|
7,63 (лін.од).
Задача 6.242. Обчислити довжину дуги кривої
222
333
2xy
, де
0
d
x
d
2.
Розв’язок. Знайдемо
y
c
:
11
33
22
0
33
xyy
c
,
звідки
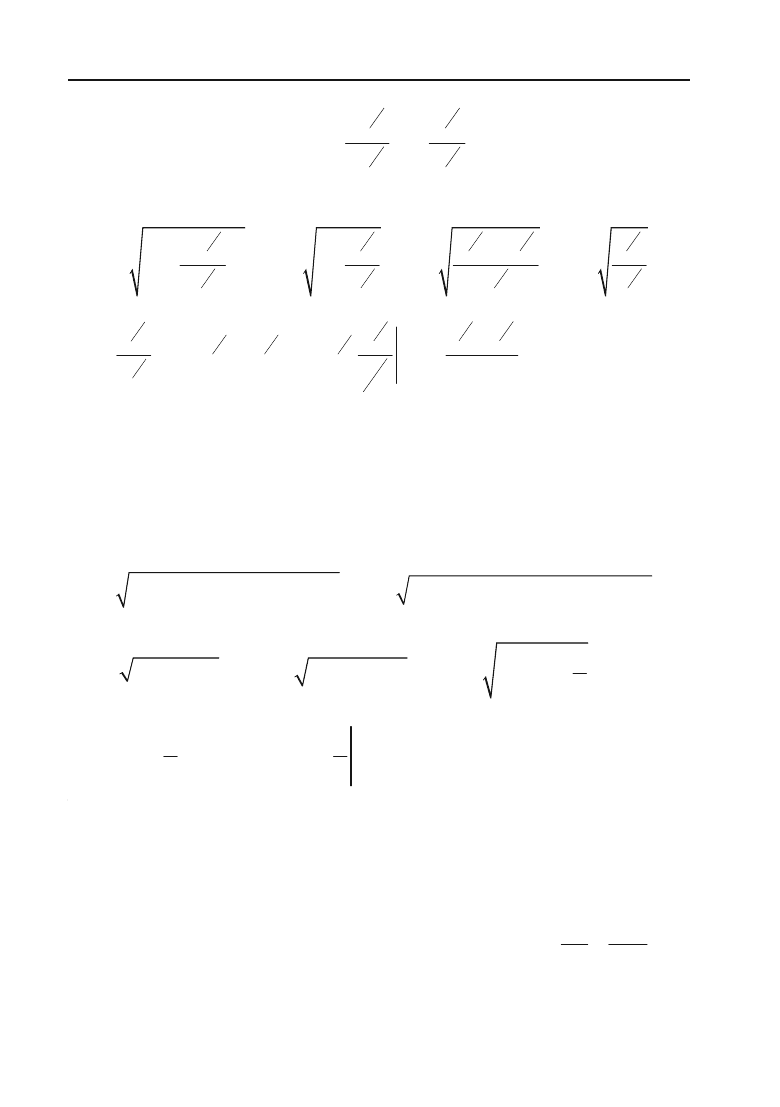
430
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
11
33
11
33
xy
y
y
x
c
.
Підставляємо у формулу (6.33) та отримуємо:
12222
2222
33333
2
1222
3 333
0000
2
1( ) 1
yyxy
ldxdxdxdx
x xxx
³³³³
1
2
3
1
3
0
2
dx
x
³
212
2
333
11 1
33 3
0
2
22
2233
2
02
3
x
xdx
³
(лін. од).
Задача 6.243. Обчислити довжину дуги кривої x = a(t – sin t),
y = a(1 – cos t), де
02t
S
dd
.
Розв’язок. Скористуємося формулою (6.34). Знайдемо:
(sin)
t
x
tt
c
, (1 cos )
t
y
t
c
.
Отримуємо:
22
2
22 22
00
(1 cos ) ( sin ) (1 2 cos cos sin )la tatdta tttdt
SS
³³
2
0
22cosatdt
S
³
2
0
2(1 cos )atdt
S
³
2
2
0
22sin
2
t
adt
S
³
=
2
0
2sin
2
t
adt
S
³
2
22cos
20
t
a
S
4
(
cos cos0
)
a
S
4
(
11
)
8aa
(лін. од.).
6.8.2.2. Задачі для самостійного розв’язку
6.244.
Обчислити довжину дуги кривої
2
ln
42
x
x
y
, де
12xdd
.
