Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


401
Розділ VI. Інтегральне числення
6.4.2. Інтеграли вигляду
³
(sin , cos )Rx xdx
Розглянемо інтеграли вигляду
(
sin , cos
)
Rx xdx
³
. Запис
R(sin x, cos x) означає, що над синусом і косинусом проводяться
тільки раціональні операції: додавання та віднімання, множення на
сталі величини, піднесення до цілого степеня як додатного, так і
від’ємного, ділення. Іншими словами, під символом R(sin x, cos x)
необхідно розуміти раціональну функцію синуса та косинуса.
Такі інтеграли приводяться до інтегралів від раціональної функції
нового аргументу t підстановкою, яку називають універсальною:
tg
2
x
= t, (
S
< x <
S
),
тоді
sin x =
2
2
1
t
t
, cos x =
2
2
1
1
t
t
, dx =
2
2
1 t
dt. (6.14)
Однак саме внаслідок універсальності ця підстановка часто при+
водить до складних інтегралів. Більш зручні наступні підстановки:
а) u = cos x, якщо R(–sin x; cos x) = –R(sin x; cos x);
б) u = sin x, якщо R(sin x; –cos x) = –R(sin x; cos x);
в) u = tg x, якщо R(–sin x; –cos x) = R(sin x; cos x).
=
1
2
4
cos
3
x
dx
³
–
1
2
8
cos
3
x
dx
³
=
1
2
3
4
44
cos
33
x
dx
³
–
–
1
2
3
8
88
cos
33
x
dx
³
=
3
8
sin
4
3
x –
3
16
sin
8
3
x + C.
6.4.2.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.130.
2sin cos
dx
x
x
³
.
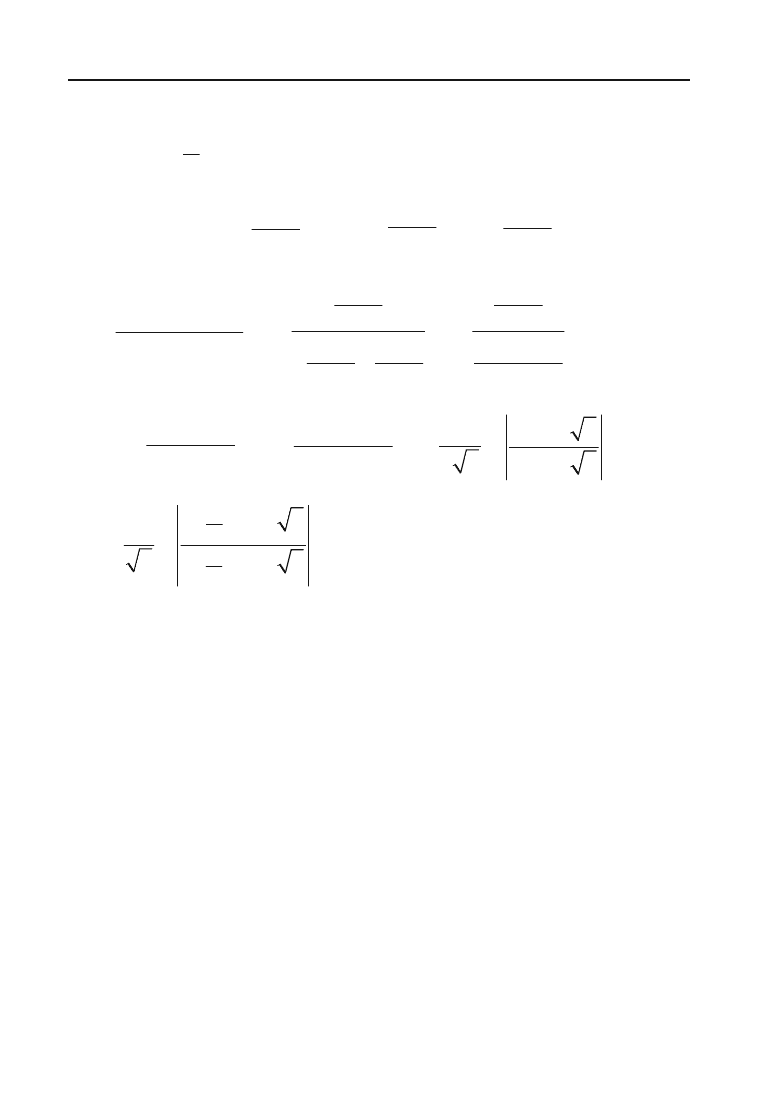
402
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.4.3. Інтеграли вигляду
³
sin cos
mn
x
xdx
I. Нехай хоча б один з показників степеня є непарне число. Не+
хай n = 2k + 1. В такому випадку підінтегральний вираз можна пере+
творити так:
sin
m
xcos
n
xdx = sin
m
xcos
2
k
+1
xdx = sin
m
xcos
2
k
xcosxdx =
= sin
m
x(cos
2
x)
k
cosxdx = sin
m
x(1 – sin
2
x)
k
cosxdx.
Застосуємо підстановку sinx = u, cosxdx = du.
І інтегральний вираз прийме вигляд u
m
(1 – u
2
)
k
du. Питання зво+
диться до інтегрування суми степеневих функцій.
Розв’язок. Використаємо універсальну тригонометричну підста+
новку t = tg
2
x
. Звідки
sin x =
2
2
1
t
t
, cos x =
2
2
1
1
t
t
, dx =
2
2
1 t
dt.
2sin cos
dx
xx
³
=
2
2
22
2
1
21
2
11
dt
t
tt
tt
³
=
2
2
2
2
1
41
1
dt
t
tt
t
³
=
= 2
2
41
dt
tt
³
= 2
2
(2)5
dt
t
³
= 2
1
25
ln
25
25
t
t
+ C =
=
1
5
ln
t
g
25
2
t
g
25
2
x
x
+ C.
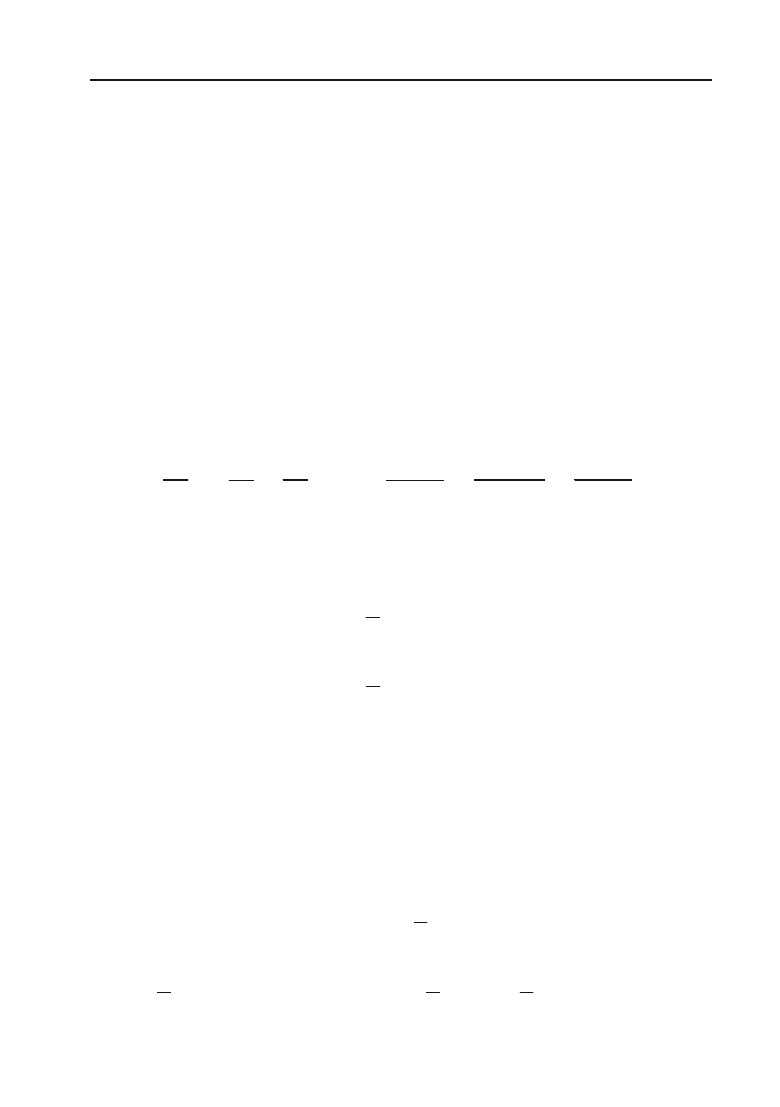
403
Розділ VI. Інтегральне числення
6.4.3.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.131.
54
sin cosxxdx
³
.
Розв’язок.
54
sin cosxxdx
³
=
44
sin sin cosxx xdx
³
=
22 4
(sin ) sin cosxxxdx
³
=
=
22 4
(1 cos ) cos sinxxxdx
³
.
Введемо підстановку: cos x = u; –sin xdx = du; sin xdx = –du.
22 4
(1 cos ) cos sin
xxxdx
³
=
22 4
(1 ) ( )uu du
³
=
= –
244
(1 2 )uuudu
³
= –
4
udu
³
+
6
2 udu
³
–
8
udu
³
=
=
5
5
u
+ 2
7
7
u
–
9
9
u
+ C = –
5
sin
5
x
+
7
2sin
7
x
–
9
sin
9
x
+ C.
II. Якщо m i n — обидва показники степеней парні числа.
Із тригонометрії відомо, що
sin
2
x =
1
2
(1 – cos 2x), (6.15)
cos
2
x =
1
2
(1 + cos 2x). (6.16)
Застосування цих формул дозволяє понизити степінь підінтег+
ральної функції в розглядуваних інтегралах.
Знайти інтеграли.
Приклад 6.132.
4
sin xdx
³
.
Розв’язок.
4
sin xdx
³
=
22
(sin )xdx
³
=
2
1
(1 cos 2 )
2
xdx
§·
¨¸
©¹
³
=
=
2
1
(1 2cos2 cos 2 )
4
xxdx
³
=
1
4
dx
³
–
1
2
cos2xdx
³
+

404
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
+
1
4
2
cos 2xdx
³
=
1
4
x –
1
4
sin2x +
1
4
1
(1 cos 4 )
2
xdx
³
=
=
1
4
x –
1
4
sin2x +
1
8
dx
³
+
1
8
cos4xdx
³
=
1
4
x –
1
4
sin2x +
+
1
8
x +
1
32
sin4x + C =
3
8
x –
1
4
sin2x +
1
32
sin4x + C.
6.4.4. Інтеграли вигляду
³
22
(sin cos )Rx, xdx
Інтеграли вигляду
22
(
sin ,cos
)
Rxxdx
³
, де R — раціональна фун+
кція над sin
2
x та cos
2
x. В такому випадку необхідно застосувати підста+
новку
tg x = z; sin
2
x =
2
2
1
z
z
; cos
2
x =
2
1
1 z
; dx =
2
1
dz
z
. (6.17)
6.4.4.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.133.
22
43cos 5sin
dx
xx
³
.
Розв’язок.
22
43cos 5sin
dx
xx
³
=
2
2
22
1
1
43 5
11
dz
z
z
zz
³
=
2
22
2
1
44 35
1
dz
z
zz
z
³
=
=
2
91
dz
z
³
=
1
3
arctg 3z + C =
1
3
arctg (3tg x) + C.
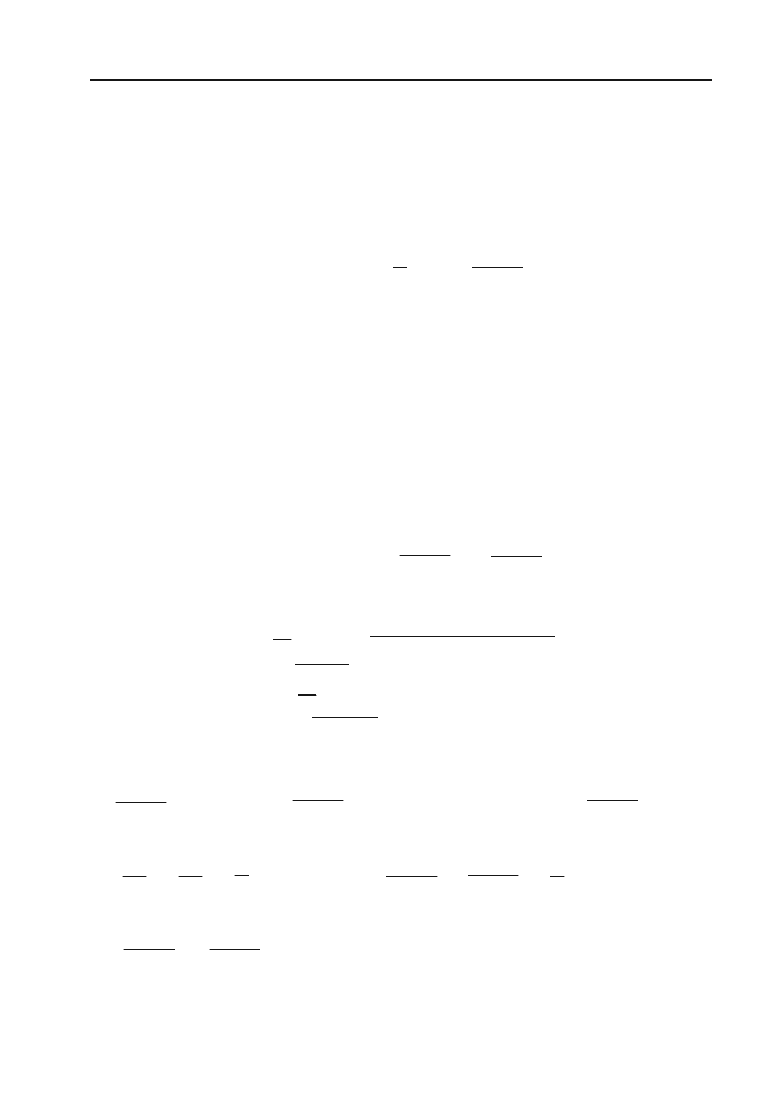
405
Розділ VI. Інтегральне числення
6.4.5. Інтеграли вигляду
³
(tg ctg )R x, x dx
Інтеграли вигляду
(
t
g
,ct
g)
Rxdx
³
, де R — раціональна функція
над tg x та ctg x. Даний інтеграл з допомогою підстановки:
tg x = z; ctg x =
1
z
; dx =
2
1
dz
z
, (6.18)
зводиться до інтегралу від дробово+раціональної функції.
6.4.5.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.134.
5
tg xdx
³
.
Розв’язок.
5
tg xdx
³
=
5
2
1
dz
z
z
³
=
5
2
1
zdz
z
³
;
5
2
1
zdz
z
³
=
3
2
()
1
z
zz dz
z
³
=
3
zdz
³
–
zdz
³
+
2
1
z
z
³
dz =
=
4
4
z
–
2
2
z
+
1
2
ln|z
2
+ 1| + C =
4
tg
4
x
–
2
tg
2
x
+
1
2
ln|tg
2
x + 1| + C =
=
4
tg
4
x
–
2
tg
2
x
– ln|cos x| + C.
z
5
|z
2
+ 1
z
5
+ z
3
|z
3
– z + z/(z
2
+ 1)
–z
3
–z
3
– z
z
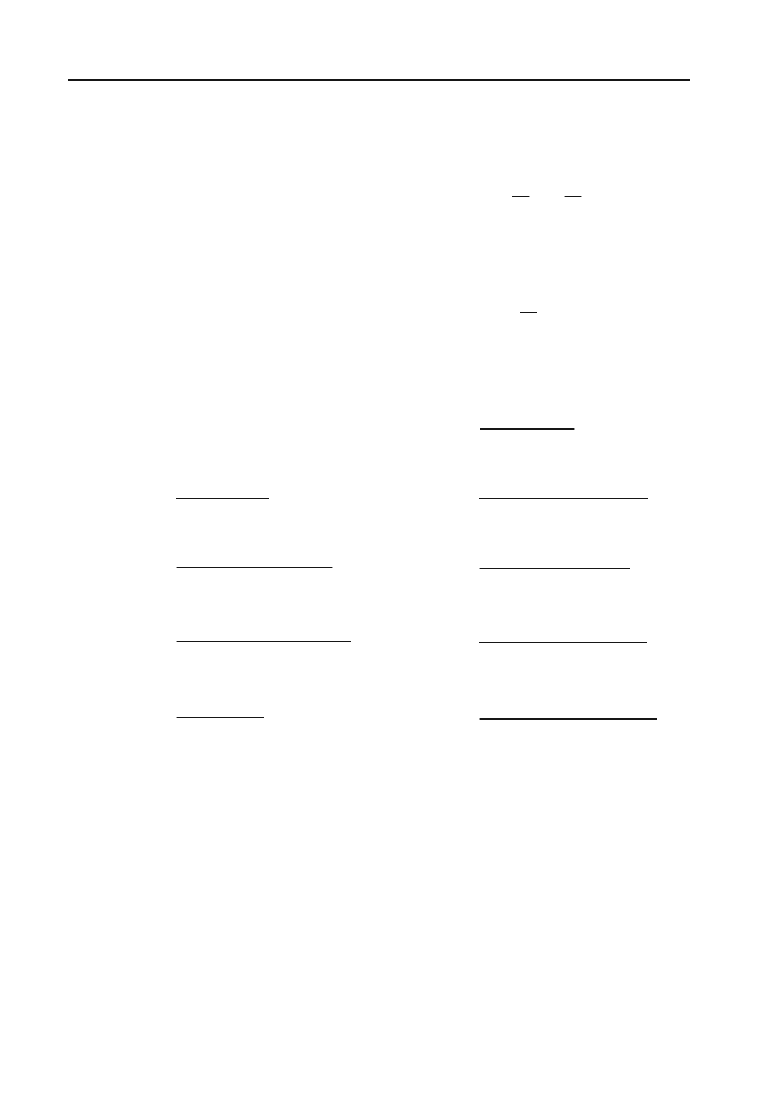
406
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.4.6. Приклади для самостійного розв’язку
Знайти інтеграли.
6.135.
sin6 cos2
xxdx
³
. 6.136.
cos cos
23
xx
dx
³
.
6.137.
sin3 sin5
xxdx
³
. 6.138.
3
sin
xdx
³
.
6.139.
5
cos xdx
³
. 6.140.
2
sin
4
x
dx
³
.
6.141.
2
cos 3
xdx
³
. 6.142.
3
sin 3
xdx
³
.
6.143.
4
tg
xdx
³
. 6.144.
23cos
dx
x
³
.
6.145.
54sin
dx
x
³
. 6.146.
3sin 2cos 1
dx
xx
³
.
6.147.
4tg 4ctg
dx
xx
³
. 6.148.
22
9tg
7sin cos
x
dx
xx
³
.
6.149.
(9 10tg )sin 2
dx
xx
³
. 6.150.
2
(2 tg )
(2sin 5cos )
xdx
xx
³
.
6.151.
74tg
dx
x
³
. 6.152.
22
(1 7 tg )
2sin cos 3
xdx
xx
³
.
407
Розділ VI. Інтегральне числення
§ 6.5. Інтегрування виразів, що містять ірраціональність
6.5.1. Інтеграли вигляду
³
5
(, ,..., )
mr
n
Rx x x dx
Розглянемо інтеграл
5
(, ,..., )
m
r
n
Rxx x dx
³
, де R — раціональна
функція своїх аргументів. Інтеграл такого вигляду знаходиться за до+
помогою підстановки:
x = t
k
; dx = kt
k
– 1
dt, (6.19)
де k — спільний знаменник дробів
m
n
, ...,
r
s
.
6.5.1.1. Розв’язання прикладів
Приклад 6.153.
Знайти інтеграл
2
3
4
x
dx
xx
³
.
Розв’язок. Спільний знаменних дробових показників
1
2
,
2
3
,
1
4
змінної х дорівнює 12. Виконаємо підстановку x = t
12
, dx = 12t
11
dt,
t =
12
x
. Одержимо:
2
3
4
x
dx
x
x
³
=
12
11
12 2 12
4
3
12
()
t
tdt
tt
³
=
611
83
12ttdt
tt
³
=
= 12
17
35
(1)
tdt
tt
³
= 12
14
5
1
tdt
t
³
.
Одержали неправильний дріб. Необхідно виділити цілу частину.
408
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.5.2. Інтеграли вигляду
, ,...,
mr
ns
ax b ax b
Rx dx
cx d cx d
§·
§·§·
¨¸
¨¸¨¸
¨¸
©¹©¹
©¹
³
Інтеграли вигляду
, ,...,
mr
ns
ax b ax b
Rx dx
cx d cx d
§·
§·§·
¨¸
¨¸¨¸
¨¸
©¹©¹
©¹
³
, де
ab
cd
z
приводяться до раціональної функції за допомогою підста+
новки
ax b
cx d
= t
k
, де k — спільний знаменник дробів
m
n
, ...,
r
s
.
12
14
5
1
tdt
t
³
= 12
4
94
5
()
1
t
tt dt
t
³
= 12
9
tdt
³
+ 12
4
tdt
³
+
+ 12
4
51
t
t
³
dt = 12
10
10
t
+ 12
5
5
t
+
12
5
ln|t
5
– 1| + C =
6
5
(
12
x
)
10
+
+
12
5
(
12
x
)
5
+
12
5
ln|(
12
x
)
5
– 1| + C =
6
5
5
6
x
+
12
5
5
12
x
+
+
12
5
ln|
5
12
x
– 1| + C.
t
14
|t
5
– 1
t
14
– t
9
|t
9
+ t
4
+ t
4
/(t
5
– 1)
t
9
t
9
– t
4
t
4
409
Розділ VI. Інтегральне числення
6.5.3. Інтеграли, що потребують тригонометричної підстановки
До інтегралів від функцій, що раціонально залежать від тригоно+
метричних функцій, приводяться інтеграли:
22
(, )Rx a x dx
³
— підстановкою x = a sin t; (6.20)
22
(, )Rx a x dx
³
— підстановкою x = a tg t; (6.21)
22
(, )Rx x a dx
³
— підстановкою x = a/cos t. (6.22)
6.5.2.1. Розв’язання прикладів
Приклад 6.154.
Знайти інтеграл
2
11
x
x
x
³
dx.
Розв’язок. Виконаємо підстановки t
2
=
1 x
x
, звідки
x =
2
1
1t
, dx =
22
2
(1)
tdt
t
.
2
11
x
x
x
³
dx =
22
22
2
(1)
(1)
tdt
t
t
³
= –2
2
tdt
³
= –2
3
3
t
+ C =
= C –
3
21
3
x
x
§·
¨¸
©¹
.
6.5.3.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.155.
22
4
x
xdx
³
.
Розв’язок. Застосовуємо підстановку x = a sin t, одержуємо
dx = 2cos tdt, і якщо sin t =
2
x
, то t = arcsin
2
x
.
410
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
22
4
x
xdx
³
=
22
(
2sin
)
44sin 2costttdt
³
=
22
4sin 4costtdt
³
=
= 4
2
sin 2tdt
³
= 4
1cos4
2
t
dt
³
= 2
dt
³
– 2
cos4tdt
³
=
= 2t –
1
2
sin4t + C = 2arcsin
2
x
–
1
2
sin4(arcsin
2
x
) + C =
= 2arcsin
2
x
+
4
x
(x
2
– 2)
2
4 x
+ C.
Приклад 6.156.
23
(36 )
dx
x
³
.
Розв’язок. Застосовуємо підстановку x = 6tg t, одержуємо
dx =
2
6
cos t
dt, і якщо x = 6tg t, то t = arctg
6
x
.
23
(
36
)
dx
x
³
=
2
23
6
cos
(36 36tg )
dx
t
t
³
=
3
6
6
2
3
cos
1
cos
dt
t
t
³
=
1
36
costdt
³
=
=
1
36
sin t + C =
1
36
sin(arctg
6
x
) + C =
1
36
2
36
x
x
+ C.
Приклад 6.157.
2
4
25
x
dx
x
³
.
Розв’язок. Застосовуємо підстановку
5
cos
x
t
, одержуємо
2
5sin
cos
tdt
dx
t
, якщо
5
cos
x
t
, cos t =
5
x
, t = arccos
5
x
.
