Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


391
Розділ VI. Інтегральне числення
=
2
A
ln|x
2
+ px + q| +
2
2
4
BAp
qp
arctg
2
2
4
xp
qp
+ C. (6.10)
Інтеграл від найпростішого дробу IV+го типу шляхом повторного
інтегрування частинами зводять до інтеграла від найпростішого дро+
бу типу III.
Інтеграл від дробово+раціональної функції
()
()
n
m
Px
dx
Qx
³
, де
()
()
n
m
Px
Qx
правильний дріб, можна знайти (виразити через елементарні
функції) шляхом розкладу на доданки, які завжди приводяться до
формул інтегрування. Будь+який
()
()
n
m
Px
Qx
правильний раціональний
дріб розкладається на суму найпростіших раціональних дробів, кое+
фіцієнти яких можна знайти методом невизначених коефіцієнтів.
Вигляд найпростіших дробів визначається коренями знаменника
()
m
Qx. Можливі наступні випадки:
1. Корені знаменника тільки дійсні та різні числа, тобто
Q
m
(x) = (x – a
1
)(x – a
2
)
…
(x – a
n
).
В цьому випадку правильний дріб
()
()
n
m
Px
Qx
розкладається на суму
найпростіших дробів 1+го типу:
12
12
()
......
()
nm
mm
Px A
AA
Qx xa xa xa
,
де A
1
, A
2
,…, A
n
— невизначені коефіцієнти, які знаходяться з тотож+
ності, що написана вище.
2. Корені знаменника тільки дійсні числа, причому деякі з них
кратні, тобто
Q
m
(x) = (x – a)
...
(x – b)
i
.

392
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.3.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.107.
2
32
22
28
xx
dx
x
xx
³
.
Розв’язок. Підінтегральна функція
2
32
22
28
xx
x
xx
— це правиль+
ний раціональний дріб, знаменник якого x
3
+ 2x
2
– 8x розкладається
на множники x(x – 2)(x + 4), тому даний дріб розкладається на суму
найпростіших дробів типу І:
Тоді правильний дріб
()
()
n
m
Px
Qx
розкладається на суму найпрості+
ших дробів 1+го та 2+го типів:
1
12
21
()
..... ......
()
() ()()
n ii
ii
m
Px B B
BB
A
Qx xa xb
xb xb xb
.
Де невизначені коефіцієнти A, …, B
1
, B
2
, …, B
i
–1
, B
i
знаходяться з
тотожності, що написана вище.
3. Корені знаменника дійсні числа, причому деякі з них кратні,
крім того знаменник містить квадратний тричлен, який не розкла+
дається на множники, тобто
Q
m
(x) = (x – a)(x – b)
i
(x
2
+ px + q).
В цьому випадку дріб
()
()
n
m
Px
Qx
розкладається на суму найпрості+
ших дробів І+го, ІІ+го та ІІІ+го типів
1
12
212
()
...
()
() ()()
nii
ii
m
Px B B
BB
AMxN
Qx xaxb
xb xb xb x pxq
,
де A, B
1
, B
2
, …, B
i
–1
, B
i
, M, N невизначені коефіціенти, які необхідно
знайти.

393
Розділ VI. Інтегральне числення
22
32
22 22
(2)(4) 2 4
28
x
xxxABC
xx x x x x
xxx
.
Невідомі коефіцієнти A, B, C будемо знаходити методом невиз+
начених коефіцієнтів. Для цього праву частину одержаної вище
рівності необхідно привести до спільного знаменника. Отримаємо
2(2)(4)(4)(2)
32
22
24
28
xx xx xx
xx A B C
xxx
x
xx
=
=
(2)(4) (4) (2)
(2)(4)
Ax x Bxx Cxx
xx x
=
=
222
28 4 2
(2)(4)
A
x Ax A Bx Bx Cx Cx
xx x
.
Знаменники в обох частинах рівні, тому і чисельники повинні
бути рівні, тобто
x
2
– 2x + 2 = Ax
2
+ 2Ax – 8A + Bx
2
+ 4Bx + Cx
2
– 2Cx,
x
2
– 2x + 2 = (A + B + C)x
2
+ (2A + 4B – 2C)x – 8A.
Остання рівність можлива лише тоді, коли коефіцієнти при од+
накових степенях х в обох частинах рівності рівні, тобто
2
0
x
x
x
1
242 2
82
ABC
ABC
A
½
°
¾
°
¿
Отримали систему рівнянь, з якої знаходимо невизначені коефі+
цієнти
4
5
3
2
4
BC
BC
°
°
®
°
°
¯
А =
1
4
,
113
,
612
BC
.
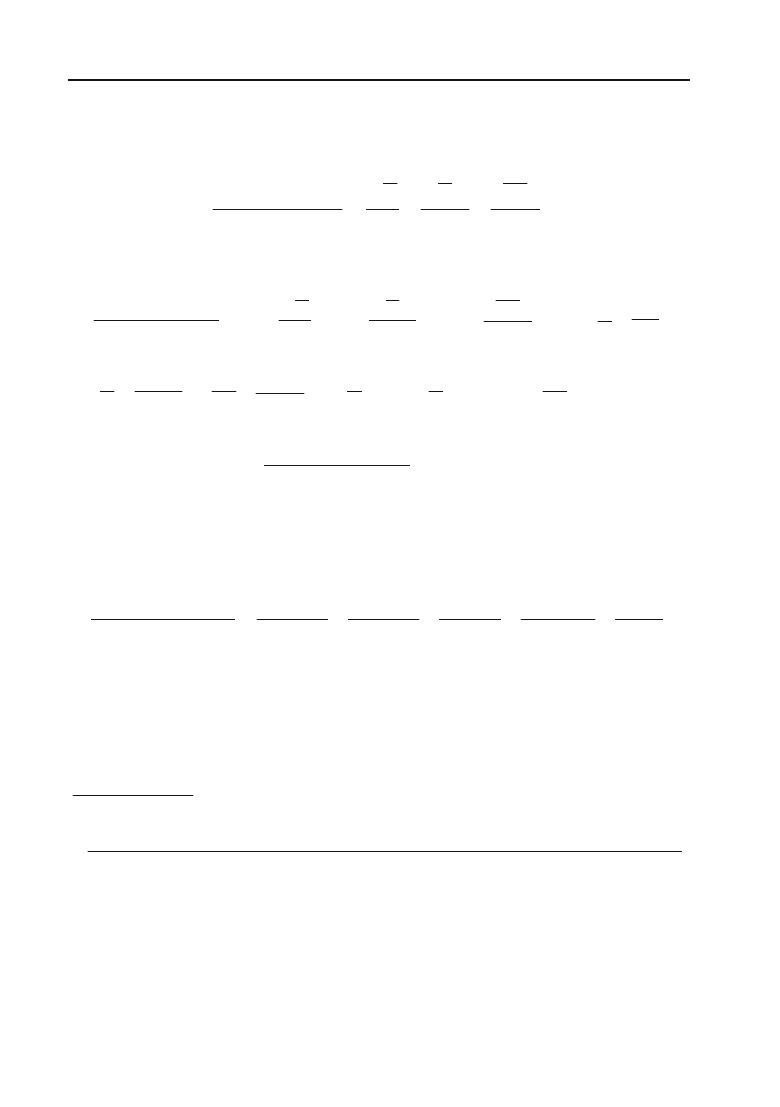
394
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Підставляємо знайдені значення A, B, C в схему розкладу і отри+
муємо розклад підінтегральної функції:
2
32
11 13
22
46 12
24
28
xx
x
xx
x
xx
.
Інтегруючи останню рівність маємо:
2
32
1
1
22
46
2
28
xx
dx dx dx
xx
x
xx
³³³
+
13
12
4x
³
dx =
1
4
dx
x
³
+
+
1
6
2
dx
x
³
+
13
12
4
dx
x
³
=
1
4
ln|x| +
1
6
ln|x – 2| +
13
12
ln|x + 4| + C.
Приклад 6.108.
2
32
258
(1)(2)
xx
dx
xx
³
.
Розв’язок. Підінтегральна функція — це правильний нескоротний
раціональний дріб, знаменник якого містить лише дійсні корені, тому
цей дріб розкладається на суму найпростіших дробів І+го та ІІ+го типу.
2
32 3 2 2
258
(1) 2(1)(2)(1)(1) (2)
x
xABCDE
xxxx x x x
.
Визначимо невідомі коефіцієнти A, B, C, D та E методом невиз+
начених коефіцієнтів та методом задання частинних значень, які
доцільно комбінувати. Праву частину рівності приведемо до спільного
знаменника, отримуємо:
2
32
22 2233
32
258
(1)(2)
( 2) ( 2) ( 1) ( 2) ( 1) ( 1) ( 1) ( 2)
(1)(2)
xx
xx
Ax Bx x Cx x Dx Ex x
xx
.
Знаменники в обох частинах рівні, тому і чисельники повинні
бути рівні:
2x
2
+ 5x – 8 = A(x + 2)
2
+ B(x + 2)
2
(x – 1) + C(x + 2)
2
(x – 1)
2
+
+ D(x –1)
3
+ E(x – 1)
3
(x + 2).

395
Розділ VI. Інтегральне числення
Нагадаємо, що отриманий вираз є тотожністю, а через це рівність
повинна зберігатися при будь+якому значенні х. При x = –2 отри+
муємо:
23
10
2( 2) 5( 2) 8 ( 2 1) 10 27
27
DDD
.
При x = 1.
22
1
21 51 8 (1 2) 1 9
9
AAA
.
Нам залишилось визначити коефіцієнти B, C, E. Тепер будемо
порівнювати коефіцієнти при однакових степенях х в лівій та правій
частинах рівності. Коефіцієнти при x
4
в лівій частині дорівнює
нулю(x
4
в лівій частині відсутній), а в правій C + E. Через це C + E = 0.
Вільний член в лівій частині дорівнює –8, а в правій
4A – 4B + 4C – D – 2E.
На основі цього отримуємо друге рівняння:
4A – 4B + 4C – D – 2E = –8,
в якому A та D відомі
110
(; )
927
AD
, маємо
97
22
27
BCE
.
Ми порівняли саме вільні члени, тому що це можливо зробити,
не виконуючи множення та піднесення до степені у правій частині
рівності.
Для того щоб отримати третє рівняння для визначення B, C і E,
знову повернемося до способу задання частинних значень.
Якщо x = 2, отримуємо:
2
2
2
+ 5
2 – 8 = 16A + 16B + 16C + D + 4E.
Знаючи, що
1
9
A
, а
10
27
D
, це рівняння прийме вигляд
77
44
27
BCE
.
Таким чином, для визначення B, C і E отримали систему рівнянь:
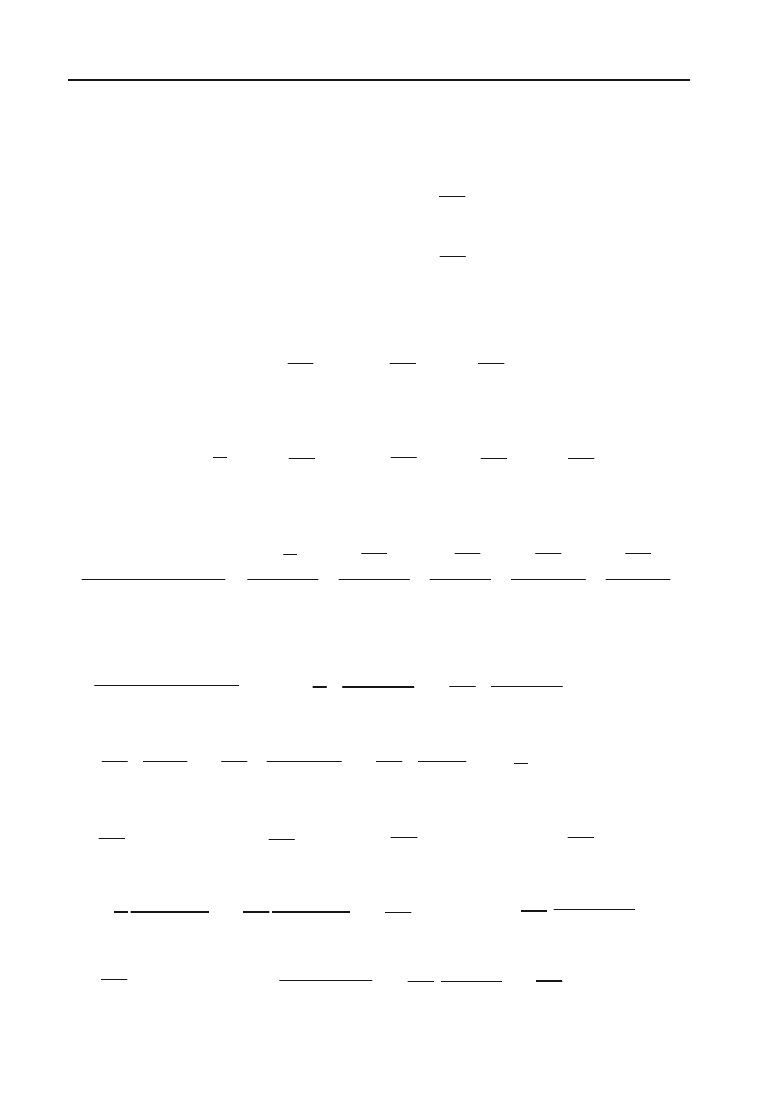
396
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
0
97
22
27
77
44
27
CE
BCE
BCE
°
°
°
®
°
°
°
¯
Розв’язавши систему, отримаємо:
29
27
B
,
13
27
C
,
13
27
E
.
Отже, маємо:
1
9
A
,
29
27
B
,
13
27
C
,
10
27
D
,
13
27
E
.
Тепер розклад підінтегральної функції має вигляд:
2
32 3 2 2
29 13 10 13
1
258
27 27 27 27
9
(1) (2)
(1)(2)(1)(1) (2)
xx
xx
xx x x x
.
Інтегруючи цю рівність, отримуємо:
2
32
258
(1)(2)
xx
dx
xx
³
= –
3
1
9
(1)
dx
x
³
+
2
29
27
(1)
dx
x
³
–
–
13
27 1
dx
x
³
+
10
27
2
(2)
dx
x
³
+
13
27 2
dx
x
³
= –
3
1
(1)
9
xdx
³
+
+
2
29
(1)
27
x
dx
³
–
13
27
ln|x – 1| +
10
27
2
(2)
x
dx
³
+
13
27
ln|x + 2| =
= –
2
1( 1)
92
x
+
1
29 ( 1)
27 1
x
–
13
27
ln|x – 1| +
10
27
1
(2)
1
x
+
+
13
27
ln|x + 2| + C =
2
1
18( 1)
x
–
29
27
1
(1)x
–
13
27
ln|x – 1| –

397
Розділ VI. Інтегральне числення
–
10
27( 2)x
+
13
27
ln|x + 2| + C.
Приклад 6.109.
32
4
421
.
xxx
dx
xx
³
Розв’язок. Підінтегральна функція – це правильний нескоротний
дріб, знаменник якого: x
4
+ x = x(x
3
+ 1) = x(x + 1)(x
2
– x + 1). Маємо,
що знаменник містить квадратний тричлен, який не розкладається
на множники, та два дійсних кореня x = 0 та x = –1, то даний дріб
розкладається на суму найпростіших дробів І+го та ІІІ+го типу
32 32
42 2
421 421
1
(1)( 1) 1
x
xx xxx ABMxN
xx
xx xx xx xx
.
Невідомі коефіцієнти A, B, M та N будемо шукати методом не+
визначених коефіцієнтів. Для цього праву частину рівності потрібно
привести до спільного знаменника, отримаємо:
32 2
32
42
(1)( 1)( )( )
421
(1)( 1)
x
A
xBxxMxNxx
xxx
xx xx xx
.
Знаменники в обох частинах рівні, тому і чисельники повинні
бути рівні, тобто:
x
3
+ 4x
2
– 2x + 1 = A(x
3
+ 1) + B
x
(x
2
– x + 1) + (Mx + N)(x
2
+ x) =
= (A + B + M)x
3
+ (–B + M + N)x
2
+ (B + N)x + A.
Прирівнюючи коефіцієнти при однакових степенях букви х ,ми
отримуємо систему рівнянь для знаходження коефіцієнтів A, B, M, N
3
2
0
x
x
x
x
1,
4,
2,
1.
ABM
BMN
BN
A
½
°
°
¾
°
°
¿
0,
4,
2,
1,
BM
BMN
BN
A
°
°
®
°
°
¯
2,
0,
2,
1.
M
N
B
A
°
°
®
°
°
¯
Отже, розклад підінтегральної функції приймає вигляд
32
42
4211220
1
1
xxx x
xx
x
xxx
.
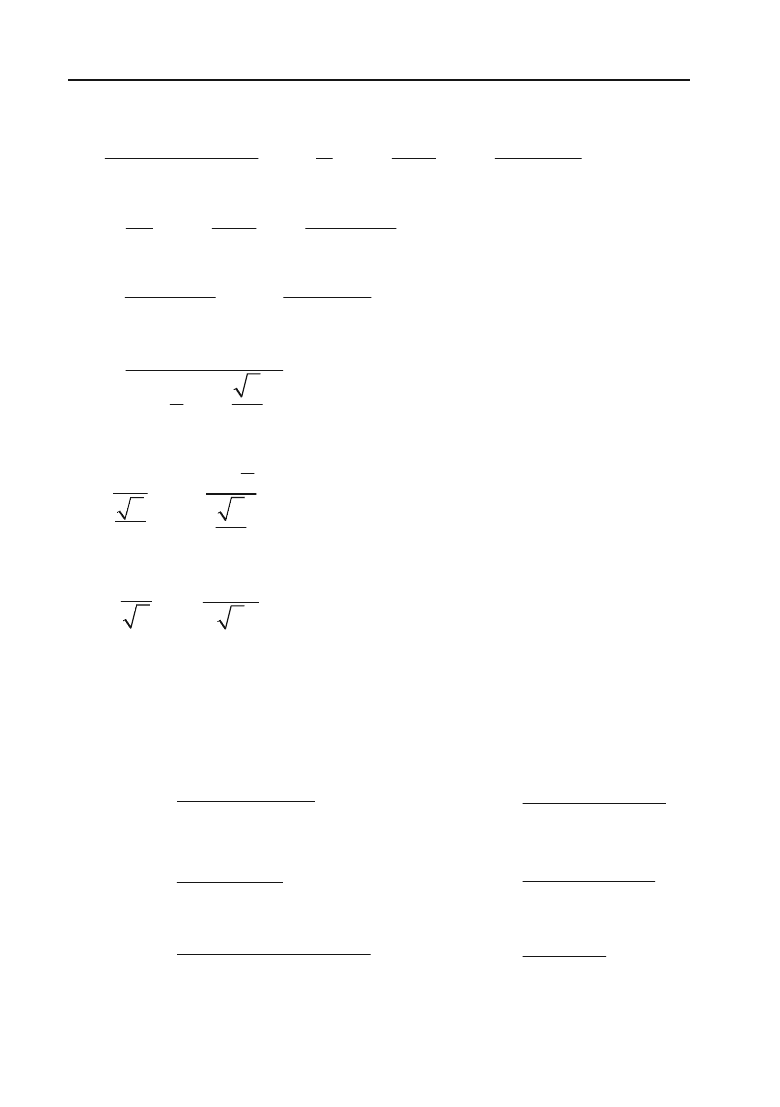
398
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.3.2. Приклади для самостійного розв’язку
Знайти інтеграли.
6.110.
( 1)(2 1)
xdx
xx
³
. 6.111.
32
673
dx
xxx
³
.
6.112.
54
3
8
4
xx
dx
xx
³
. 6.113.
2
32
38
44
x
dx
xxx
³
.
6.114.
42
223
(1)(2)(3)
xxx
dx
xxx
³
. 6.115.
32
2
2
x
dx
x
x
³
.
Інтегруючи цю рівність, отримаємо:
32
42
421 1 2 2
11
x
xx xdx
dx dx dx
xxxx xx
³³³³
=
=
dx
x
³
– 2
1
dx
x
³
+
2
211
1
x
dx
xx
³
= ln|x| – 2ln|x + 1| +
+
2
21
1
x
dx
xx
³
+
2
1
dx
xx
³
= ln|x| – 2ln|x+1| + ln|x
2
– x + 1| +
+
22
13
()()
22
dx
x
³
= ln|x| – 2ln|x + 1| + ln|x
2
– x + 1| +
+
1
3
2
arctg
1
2
3
2
x
+ C = ln|x| – 2ln|x + 1| + ln|x
2
– x + 1| +
+
2
3
arctg
21
3
x
+ C.
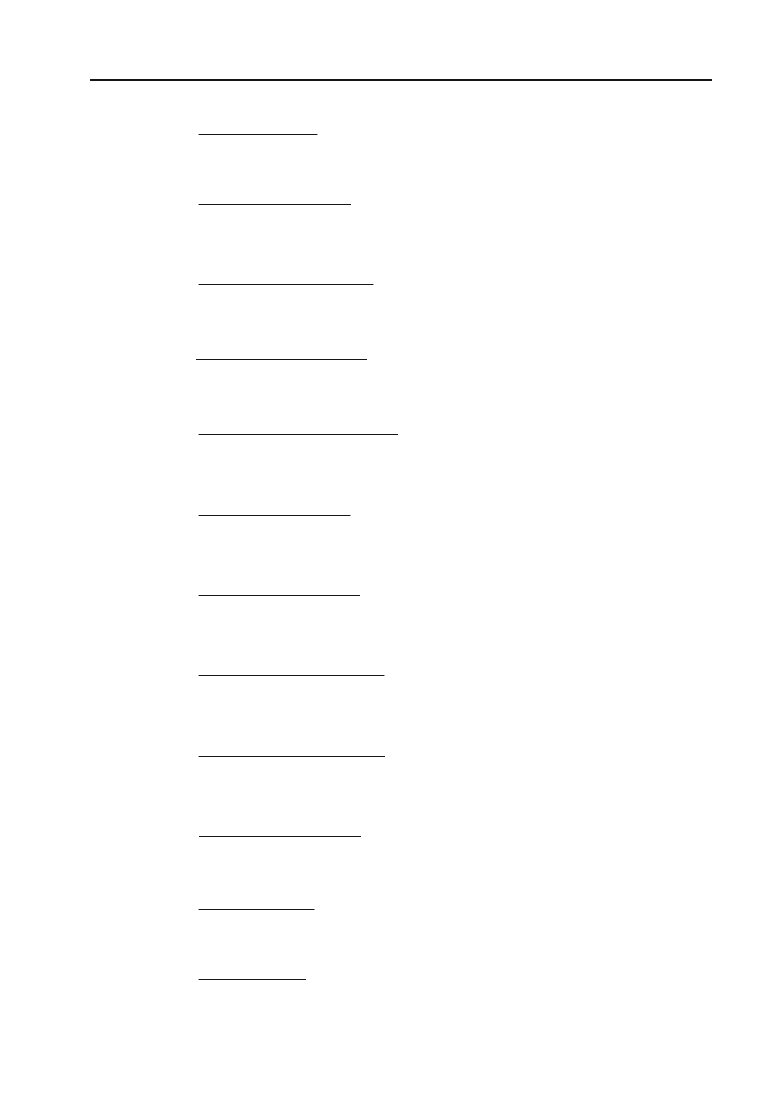
399
Розділ VI. Інтегральне числення
6.116.
2
32
251
2
xx
dx
xxx
³
.
6.117.
22
(3)(2)
dx
xx
³
.
6.118.
32
22
25 4
(1)(2)
xxx
dx
xx
³
.
6.119.
2
2
315
(1)( 413)
x
dx
xxx
³
.
6.120.
2
2
711
(1)( 610)
xx
dx
xxx
³
.
6.121.
2
22
2619
(1)(2)
xx
dx
xx
³
.
6.122.
2
22
(2 8 27)
(3)( 2)
xx
dx
xx
³
.
6.123.
2
22
(2 4 3)
(1)(2)
xx
dx
xx x
³
.
6.224.
2
22
472
(1)(4)
xx
dx
xx x
³
.
6.125.
2
32
(1)
331
xdx
xxx
³
.
6.226.
2
42
25
56
x
dx
xx
³
.
6.127.
3
51
32
x
dx
xx
³
.
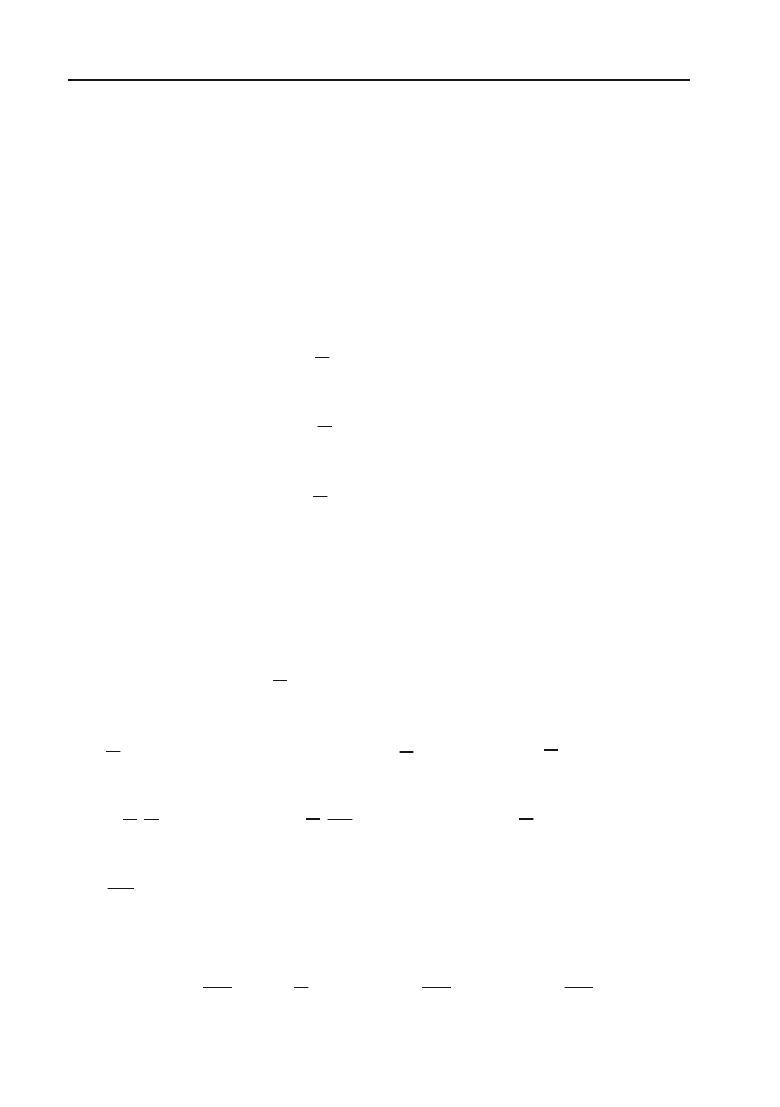
400
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§ 6.4. Інтегрування тригонометричних виразів
6.4.1. Інтеграли вигляду
³
sin coskx lxdx
;
³
cos coskx lxdx
;
³
sin sinkx lxdx
Інтеграли вигляду
sin coskx lxdx
³
;
cos coskx lxdx
³
;
sin sinkx lxdx
³
,
де l та k — дійсні числа, l
z
k, знаходяться за допомогою формул:
sinkx coslx =
1
2
(sin(k – l)x + sin(k + l)x); (6.11)
coskx coslx =
1
2
(cos(k – l)x + cos(k + l)x); (6.12)
sinkx sinlx =
1
2
(cos(k – l)x – cos(k + l)x). (6.12)
6.4.1.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.128.
sin3 cos7
xxdx
³
=
1
2
(
sin
(
37
)
sin
(
37
))
xxdx
³
=
=
1
2
(
sin
(
4
)
sin10
)
xxdx
³
=
1
2
sin4xdx
³
+
1
2
sin10xdx
³
=
=
1
2
1
4
sin4 4xdx
³
+
1
2
1
10
sin10 10xdx
³
=
1
8
cos 4x –
–
1
20
cos 10x + C.
Приклад 6.129.
2
sin2 sin
3
x
xdx
³
=
1
2
22
(cos(2 ) cos(2 ))
33
xx
xxdx
³
=
