Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


381
Розділ VI. Інтегральне числення
Одержали інтеграл, який позначали через
.
Таким чином,
=
1
b
e
ax
sin
bx +
2
a
b
e
ax
cos
bx –
2
2
a
b
.
Ми одержали рівняння з невідомою величиною
.
Перенесемо
останній
доданок в ліву частину рівняння, знайдемо:
+
2
2
a
b
=
1
b
e
ax
sin
bx +
2
a
b
e
ax
cos
bx.
Винесемо в лівій частині цього рівняння
за дужки:
22
2
ab
b
=
1
b
e
ax
(sin
bx +
a
b
e
ax
cos
bx
).
Звідки знаходимо значення інтегралу
.
=
cos
ax
ebxdx
³
=
2
22
1b
b
ba
e
ax
(sin
bx +
a
b
e
a
x
cos
bx
)
+ С =
=
22
ax
e
ab
(
b
sin
bx + a
cos
bx
)
+ С.
6.2.3.2. Приклади для самостійного розв’язку
Знайти інтеграли.
6.56.
2
ln x
dx
x
³
.
6.57.
2
x
xe dx
³
.
6.58.
3
lnxxdx
³
.
6.59.
cos3xxdx
³
.
6.60.
2
sin
x
dx
x
³
.
6.61.
sin
2
x
xxdx
³
.
6.62.
2
2
ln x
dx
x
³
.
6.63.
2
sin4
xxdx
³
.

382
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.2.4. Метод заміни змінної (метод підстановки)
Якщо заданий інтеграл
()
f
xdx
³
не може бути знайдений без+
посередньо за основними формулами, то введенням нової незалеж+
ної змінної в багатьох випадках вдається перетворити підінтеграль+
ний вираз
f
(
x
)
dx
. При цьому інтеграл зводиться до табличного або
до такого, спосіб обчислення якого відомий. Заміна змінної інтег+
рування і складає суть методу, що називається методом підстанов+
ки. Незалежну змінну замінюють за формулою
()
x
t
M
, де
()
t
M
—
диференційована функція аргументу
t
. Після цього знаходять
dx =
()
t
M
c
dt
, і інтеграл
()
f
xdx
³
приводять до
(() ()
ttdt
MM
c
³
.
()
f
xdx
³
=
(() ()
ttdt
MM
c
³
=
()
Ftdt
³
.
(6.7)
Якщо одержаний інтеграл з новою змінною інтегрування
t
буде
знайдено, то перетворивши результат до змінної
х
, використовуючи
формулу
()
xt
M
, одержимо шуканий вираз заданого інтеграла.
6.64.
2
2
x
xe dx
³
.
6.65.
23
x
xe dx
³
.
6.66.
2
cosxxdx
³
.
6.67.
2
ln
(
1
)
xxdx
³
.
6.68.
2
2
arctg
1
xx
dx
x
³
.
6.69.
2
2
5
x
xdx
³
.
6.70.
cosln xdx
³
.
6.71.
3
sin2
x
exdx
³
.
6.72.
arct
g
41xdx
³
.
6.73.
22
(
3
)
ln
(
3
)
xxdx
³
.
6.74.
2
ln
(
16 9
)
xdx
³
.
6.75.
3
sin 3
cos 3
xx
dx
x
³
.
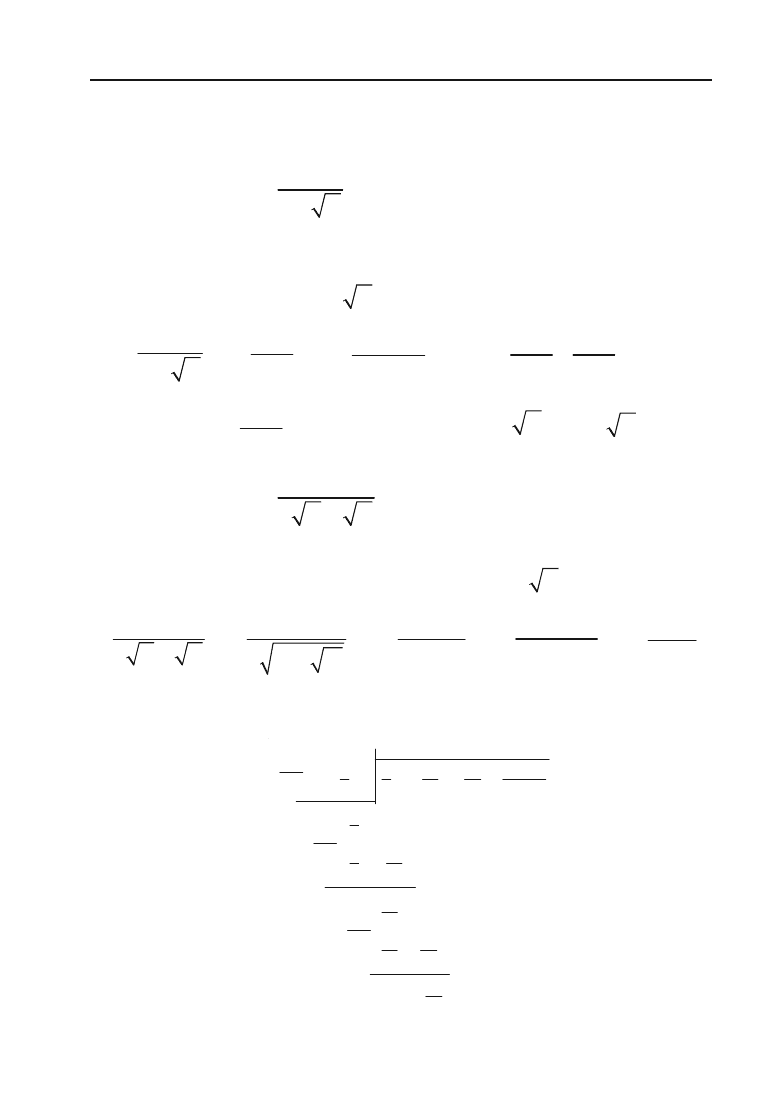
383
Розділ VI. Інтегральне числення
6.2.4.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.76.
2
dx
x
³
.
Розв’язок.
Замість змінної
х
введемо нову змінну
t
так, щоб поз+
бутися квадратного кореня
x = t
2
,
dx =
2
tdt, t =
x
.
2
dx
x
³
=
2
2
tdt
t
³
=
2
22
2
t
t
³
dt =
2
22
22
t
tt
§·
¨¸
©¹
³
dt =
= 2
dt
³
–
4
2
dt
t
³
=
2
t –
4ln
|t +
2
| + C =
2
x
–
4ln
|
x
+
2
| + C.
Приклад 6.77.
3
4
dx
x
x
³
.
Розв’язок.
Вводимо підстановку
x = t
6
так, щоб добувалися квад+
ратний та кубічний корені. Тоді
dx =
6
t
5
dt
,
t =
6
x
.
Маємо:
3
4
dx
xx
³
=
5
66
3
6
4
tdt
tt
³
=
6
5
32
4
tdt
tt
³
= 6
5
2
(4 1)
tdt
tt
³
= 6
3
41
tdt
t
³
.
Під знаком інтеграла одержали неправильний дріб, виділимо цілу
частину і правильний дріб. Для цього поділимо
t
3
на 4
t +
1.
t
3
4t + 1
t
3
+
1
4
t
2
1
4
t
2
–
1
16
t +
1
64
+
1/64
41t
1
4
t
2
1
4
t
2
–
1
16
t
1
16
t
1
16
t +
1
64
–
1
64

384
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Повернемося до інтегралу
6
3
41
tdt
t
³
=
6
2
111164
4166441
tt dt
t
§·
¨¸
©¹
³
=
6
4
2
tdt
³
–
6
16
tdt
³
+
+
6
64
dt
³
–
6
64
41
dt
t
³
=
3
3
23
t
–
2
3
82
t
+
3
32
t –
3
32
1
4
ln
|
4
t +
1
| + C.
Повернемося до змінної
x = t
6
, де
t
=
6
x
.
3
4
dx
xx
³
=
3
6
1
()
2
x
–
2
6
3
()
16
x
+
6
3
32
x
–
3
128
ln
|
4
6
x
+
1
| + C =
=
1
2
x
–
3
3
16
x
+
6
3
32
x
–
3
128
ln
|
4
6
x
+
1
| + C.
Приклад 6.78.
ln tg
sin cos
x
dx
x
x
³
.
Розв’язок.
Нехай
t =
ln tg
x
, тоді
dt =
2
11
tg
cos
x
x
dx =
sin cos
dx
xx
.
Розглядаємо:
ln tg
sin cos
x
dx
xx
³
=
lntg
sin cos
dx
x
xx
³
=
tdt
³
=
2
2
t
+ C =
=
2
(ln tg )
2
x
+ C.
6.2.4.2. Приклади для самостійного розв’язку
6.79.
1
2
x
dx
xx
³
.
6.80.
1
dx
x
³
.
6.81.
3
x
dx
x
x
³
.
6.82.
23
4
x
dx
x
x
³
.
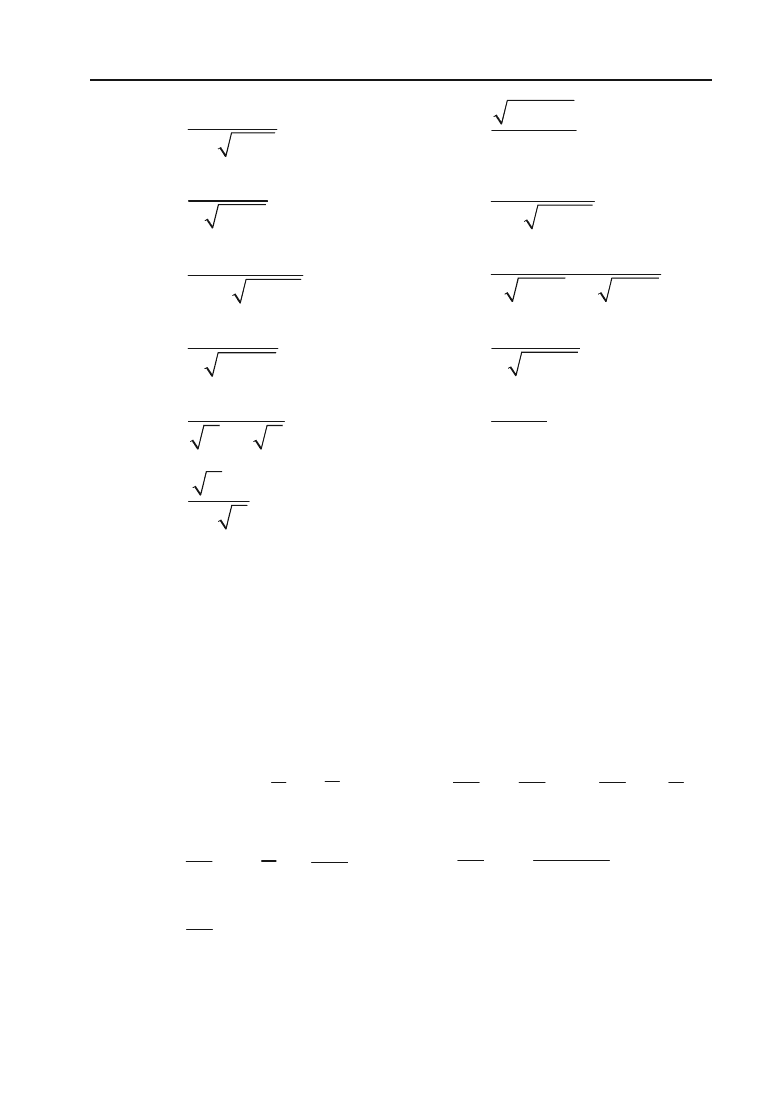
385
Розділ VI. Інтегральне числення
6.83.
3
11
dx
x
³
.
6.84.
1ln
ln
x
dx
x
x
³
.
6.85.
14
3
x
xx
³
dx
.
6.86.
3
251
dx
x
³
.
6.87.
3
3213
dx
x
³
.
6.88.
3
2434
dx
xx
³
.
6.89.
(4 )
25
x
dx
x
x
³
.
6.90.
2
51
x
dx
xx
³
.
6.91.
3
4
dx
x
x
³
.
6.92.
ln
dx
xx
³
.
6.93.
1
x
dx
x
³
.
6.2.5. Інтеграли від функцій, що містять квадратний
тричлен в знаменнику дробу
Для знаходження інтегралів від функцій, що містять квадратний
тричлен, для перетворення їх до формул інтегрування необхідно
спочатку виділити повний квадрат із квадратного тричлена, в резуль+
таті чого він перетвориться на квадратний двочлен.
ax
2
+ bx + c = a
(
x
2
+
b
a
x +
c
a
)
= a
(
x
2
+
2
x
2
b
a
+
2
2
b
a
§·
¨¸
©¹
–
2
2
b
a
§·
¨¸
©¹
+
c
a
)=
= a
((
x +
2
b
a
)
2
+
c
a
–
2
2
4
b
a
)
= a
((
x +
2
b
a
)
2
+
2
2
4
4
ac b
a
)
=
= a
((
x +
2
b
a
)
2
r
k
2
)
.
Подальше інтеграли вказаних видів можна звести до формул
інтегрування.
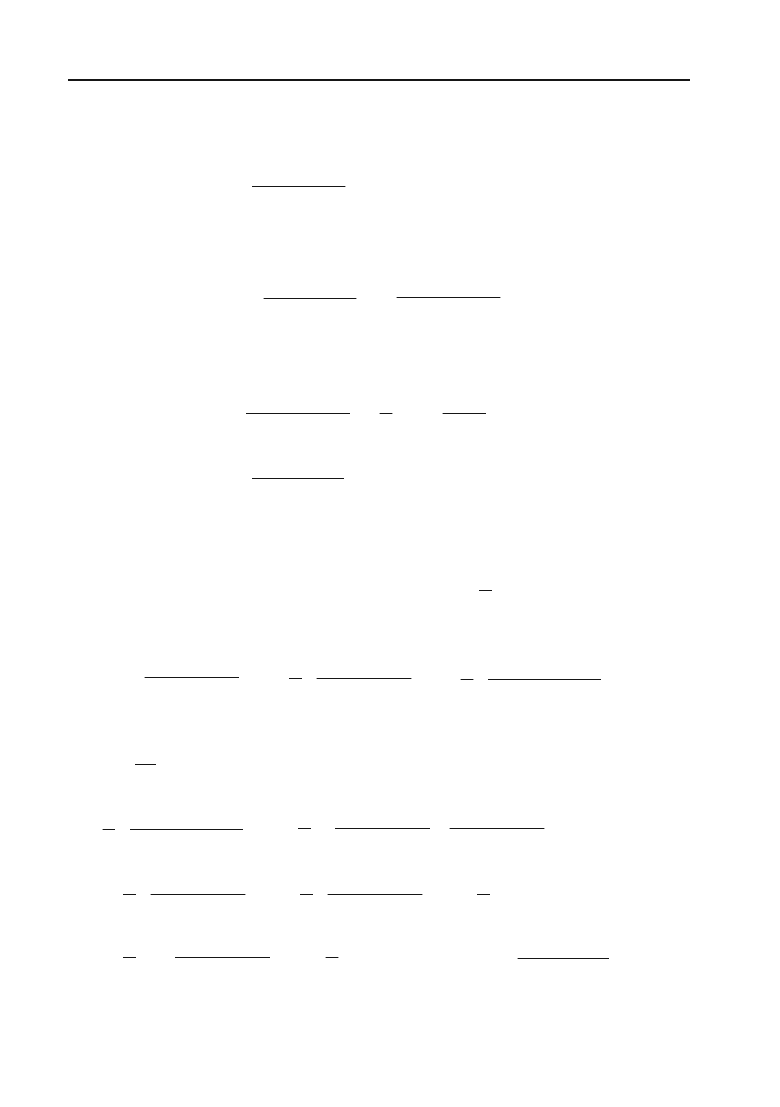
386
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.2.5.1. Розв’язання прикладів
Знайти інтеграли.
Приклад 6.94.
2
48
dx
x
x
³
.
Розв’язок.
Виділимо із квадратного тричлена повний квадрат
x
2
+
4
x
+ 8
= x
2
+
2
2
x +
2
2
–
2
2
+
8
=
(
x +
2)
2
+
4
=
(
x +
2)
2
+
2
2
.
2
48
dx
x
x
³
=
22
(
2
)
2
dx
x
³
.
Позначимо
x +
2
= v, a =
2,
тоді
dx = dv.
Використаємо формулу
(10) основних формул інтегрування:
22
(
2
)
2
dx
x
³
=
1
2
arctg
2
2
x
+ C.
Приклад 6.95.
2
3
25
x
dx
x
x
³
.
Розв’язок.
Нехай
t = x
2
–
2
x –
5,
звідки
dt =
(2
x –
2)
dx.
Щоб
одержати в чисельнику (2
x –
2)
dx,
спочатку вираз (
х +
3) помножи+
мо на 2, а потім поділимо на 2. Одержали
1
2
(2
х +
6), а потім від
одержаного виразу віднімемо 2, та додамо таке ж число:
2
3
25
x
dx
x
x
³
=
2
12(3)
2
25
x
dx
x
x
³
=
2
12 622
2
25
x
dx
x
x
³
.
Розіб’ємо на доданки так, щоб перший інтеграл зводився до фор+
мули
dt
t
³
=
ln
|t| + C.
2
12 622
2
25
x
dx
x
x
³
=
22
122 62
2
25 25
x
dx
xx xx
§·
¨¸
©¹
³
=
=
2
122
2
25
x
dx
x
x
³
+
2
18
2
25
dx
x
x
³
=
1
2
ln
|x
2
–
2
x –
5
| +
+
1
2
8
2
8
25
dx
x
x
³
=
1
2
ln
|x
2
– 2
x –
5| + 4
2
25
dx
x
x
³
.
В останньому інтегралі виділимо повний квадрат:
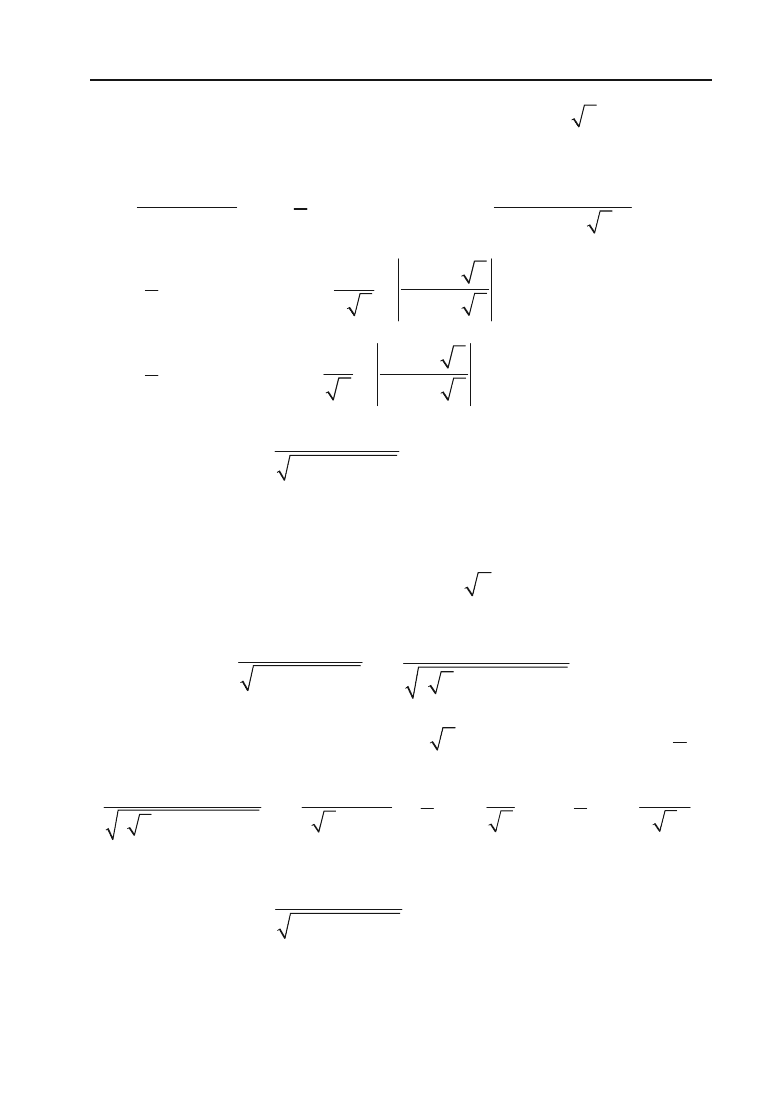
387
Розділ VI. Інтегральне числення
x
2
–
2
x –
5
= x
2
–
2
x +
1 – 1 – 5
= (
x –
1)
2
–
2
6
.
та застосуємо формулу (11).
2
3
25
x
dx
xx
³
=
1
2
ln
|x
2
–
2
x –
5
| +
4
22
(1)(6)
dx
x
³
=
=
1
2
ln
|x
2
–
2
x –
5
| +
4
1
26
ln
16
16
x
x
+ C =
=
1
2
ln
|x
2
–
2
x –
5
| +
2
6
ln
16
16
x
x
+ C.
Приклад 6.96.
2
26 9
dx
xx
³
.
Розв’язок.
Перетворимо тричлен 2
–
6
х –
9
х
2
, виділивши повний
квадрат:
2 – 6
х –
9
х
2
=
–(9
x
2
+
6
x –
2)
= –
((3
x
)
2
+
2
3
x +
1 – 1 – 2)
=
= –((3
x
+ 1)
2
–
3)
=
3 – (3
x
+ 1)
2
=
(
3
)
2
–
(3
x +
1)
2
.
Маємо
2
26 9
dx
xx
³
=
22
(3) (3 1)
dx
x
³
.
Позначимо через
u =
3
x +
1,
a =
3
, звідки 3
dx = du
,
dx =
1
3
du
22
(
3
)(
31
)
dx
x
³
=
22
1/3
(3)
du
u
³
=
1
3
arcsin
3
u
+ C =
1
3
arcsin
31
3
x
+
+ C.
Приклад 6.97.
2
53
410
x
dx
xx
³
.
Розв’язок.
Квадратний тричлен
x
2
+
4
x +
10
= t
, звідси
dt =
(2
x +
4)
dx.
Перетворимо чисельник так, щоб він містив вираз
dt =
(2
x +
4)
dx.
388
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
(5
x +
3)
=
5
2
(
2
5
(5
x +
3)
=
5
2
(2
x +
6
5
)
=
5
2
(2
x +
4 +
6
5
– 4)
=
=
5
2
((2
x
+ 4)
–
14
5
)
=
5
2
(2
x +
4) – 7
.
2
53
410
x
dx
xx
³
=
2
5/2
(
24
)
7
410
x
dx
xx
³
=
5
2
2
24
410
x
dx
xx
³
–
–
7
2
410
dx
xx
³
=
5
2
2
24
410
x
dx
xx
³
–
7
2
(
2
)
6
dx
x
³
=
=
5
2
dt
t
³
–
7ln
|x +
2
+
2
410xx
| + C =
5
2
1/2
t
–
–
7ln
|x +
2
+
2
410xx
| + C =
5
2
410xx
–
–
7ln
|x +
2
+
2
410xx
| + C.
6.2.5.2. Приклади для самостійного розв’язку
Знайти інтеграли.
6.98.
2
710
dx
xx
³
.
6.99.
2
445
dx
xx
³
.
6.100.
2
964
dx
xx
³
.
6.101.
2
41
445
x
dx
xx
³
.
6.102.
2
2
712
x
dx
xx
³
.
6.103.
2
43
dx
xx
³
.
6.104.
2
26 9
dx
xx
³
. 6.105.
2
(3 1)
22
xdx
xx
³
.
6.106.
2
(3)
32
xdx
xx
³
.

389
Розділ VI. Інтегральне числення
§ 6.3. Поняття раціонального дробу.
Інтегрування раціональних дробів
Дріб
()
()
n
m
Px
Qx
називається
раціональним
, якщо його чисельник
P
n
(
x
) та знаменник
Q
m
(
x
) є многочлени. Раціональний дріб називаєть+
ся
правильним
, якщо найвищий показник степеня його чисельника
n
менший від найвищого степеня знаменника
m
. У противному випад+
ку дріб називається
неправильним
. Інтегруються лише правильні
дробі. Неправильний раціональний дріб, у якого степінь чисельника
вищий або дорівнює степені знаменника, можна діленням чисельни+
ка на знаменник представити його у вигляді суми многочлена та
правильного раціонального дробу, в якого степінь чисельника ниж+
чий за степінь знаменника.
Наприклад.
Задано неправильний дріб
4
2
445
21
xx
xx
.
Поділимо чисельник на знаменник:
Отримали:
4
2
445
21
xx
x
x
= 4
x
2
+ 8
x
+ 12 +
2
12 7
21
x
xx
.
Найпростішими раціональними дробами І, ІІ, ІІІ та ІV
називають
правильні дроби вигляду:
I.
2
A
x
.
4x
4
– 4x + 5
«
x
2
– 2x + 1
—
4x
4
– 8x
3
+ 4x
2
«
4x
2
+ 8x + 12
8x
3
– 4x
2
– 4x + 5
—
8x
3
– 16x
2
+ 8x
12x
2
– 12x + 5
—
12x
2
– 24x + 12
12x – 7
390
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
II.
()
k
A
xa
, (
k
t
2, ціле додатне число).
III.
2
Ax B
xpxq
,
2
(0)
4
p
q
.
VI.
2
()
k
Ax B
xpxq
, (
k
t
2, ціле додатне число і
2
0
4
p
q
).
Умова
2
0
4
p
q
означає, що квадратний тричлен
x
2
+ px + q
не
має дійсних коренів і на множники не розкладається.
Розглянемо інтегрування найпростіших раціональних дробів.
Інтеграли від найпростіших раціональних дробів І+го та ІІ+го типів
знаходять методом безпосереднього інтегрування.
І.
ln
Adx
dx A A x a C
xa xa
³³
. (6.8)
ІІ.
1
1
()
()
1
() (1)()
k
k
k k
AxaA
dx A x a dx A C
k
xa k xa
³³
. (6.9)
При інтегруванні найпростішого дробу ІІІ+го типу необхідно ви+
конати перетворення.
ІІІ.
22
(2 ) ( )
22
AAp
xp B
Ax B
dx dx
x pxq x pxq
³³
=
=
2
(2 )
2
Axp
dx
xpxq
³
+ (
В –
2
Ap
)
2
dx
xpxq
³
=
=
2
A
|
ln
x
2
+ px + q| +
2
2
BAp
2
2
()( )
4
2
dx
pp
xq
³
=
=
2
A
|
ln
x
2
+ px + q|
+
2
2
BAp
2
1
4
2
qp
arctg
2
2
4
2
p
x
qp
+ C =
