Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

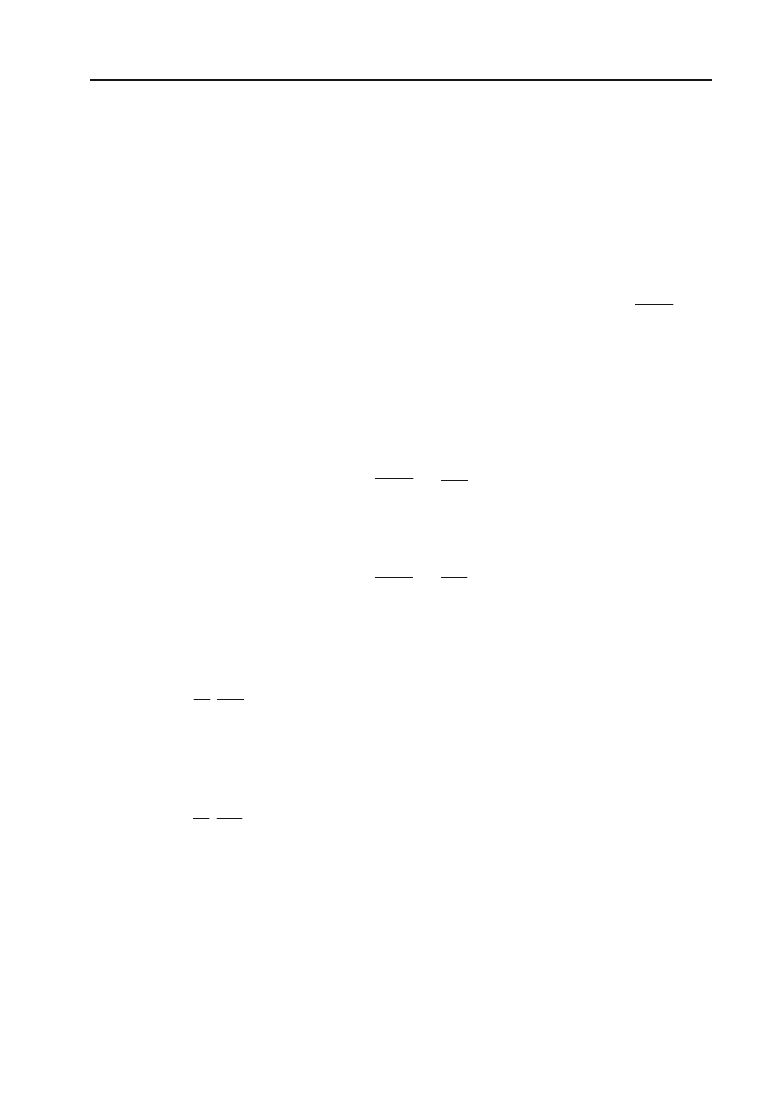
361
Розділ V. Диференціальне числення функції багатьох змінних
§5.4. Економічні задачі, що зводяться до використання
функцій багатьох змінних
Приведемо економічне тлумачення поняття частинних похідних.
Розглянемо виробничу функцію
z = f
(
x
,
y
),
яка виражає витрати
виробництва в залежності від кількості двох видів продукції
х
та
у
,
що випускається. Нехай чинник
х
змінився на
'
х
, тоді виробнича
функція зміниться на
y
z'
= f(x +
'
x
,
y) – f
(
x
,
y
)
.
Вираз
x
z
x
'
'
ви+
ражає середній приріст виробничої функції на одиницю приросту
чинника
х
, або середні витрати виробництва на одиницю продукції
х
. Здійснимо граничний перехід при
'
х
o
0. Отримаємо граничні
витрати виробництва на одиницю продукції
х
:
0
lim
x
'o
x
z
x
'
'
=
дz
дx
.
Провівши аналогічні міркування з чинником
у
, одержимо:
0
lim
y'o
y
z
y
'
'
=
дz
дy
.
Еластичність виробничої функції
z = f
(
x
,
y
) відносно чинників
виробництва
х
та
у
встановлюється так:
Е
х
(
z
)
=
x
z
дz
дx
вказує приблизно відсотковий приріст виробничої
функції (зниження) відповідно до приросту чинника
х
на 1% за умо+
ви, що чинник
у
не змінюється;
Е
у
(
z
)
=
y
z
дz
дy
вказує приблизно відсотковий приріст виробничої
функції відносно до приросту чинника
у
на 1% за умови, що чинник
х
не змінюється.
Якщо виробнича функція встановлює залежність випуску
у
від
n
виробничих чинників
х
1
,
х
2
, .
..
,
х
n
у вигляді
у = f
(
х
1
,
х
2
, ... ,
х
n
), то
диференціальними характеристиками такої функції є:
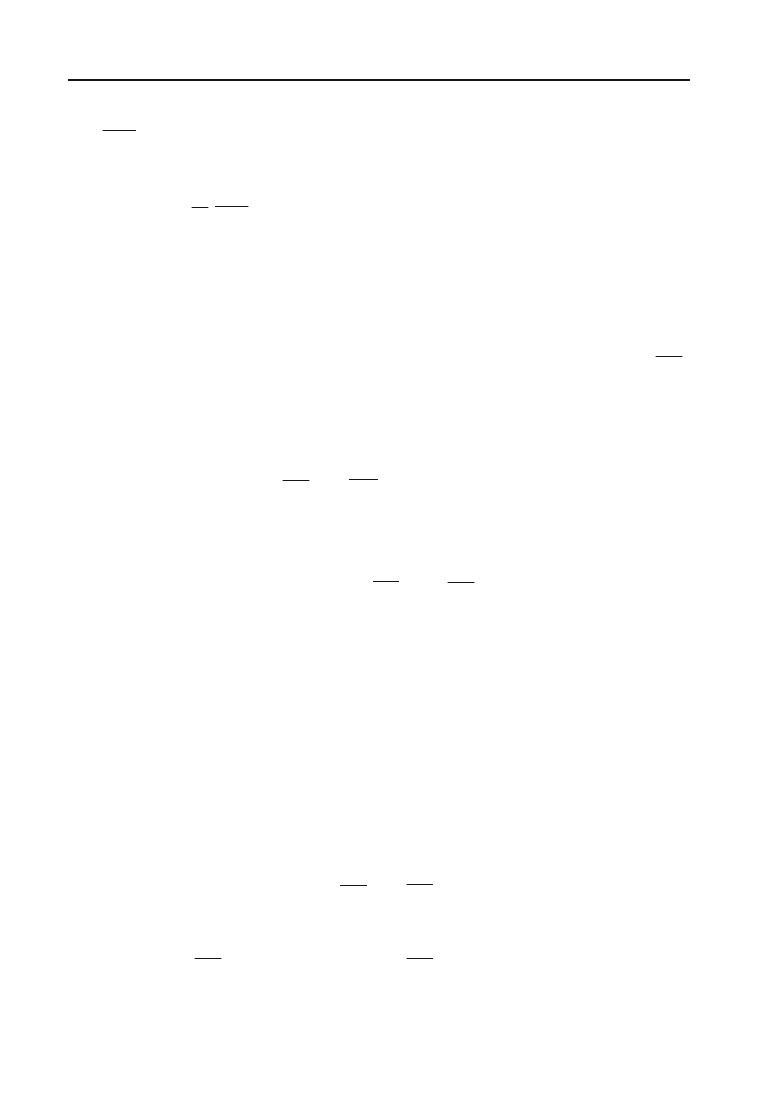
362
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
5.4.1. Розв’язання прикладів
Приклад 5.69.
Потік пасажирів
z
виражається функцією
z =
2
x
y
,
де
х
— число жителів,
у
— відстань між містами. Знайти частинні
похідні і пояснити їхній зміст.
Розв’язок.
Похідна
дz
дx
=
2
x
y
показує, що при одній і тій же
відстані між містами збільшення потоку пасажирів пропорційне под+
воєному числу жителів. Похідна
дz
дy
=
2
2
x
y
показує, що при одній
і тій же чисельності жителів збільшення потоку пасажирів обернено
пропорційне квадрату відстані між містами.
Приклад 5.70.
Для випуску деякого товару визначена виробнича
функція
f
(
x
,
y
)
=
20
х +
10
у –
2
у
2
+
4
х
2
+
3
ху
, де
х
та
у
— чинники
виробництва. Визначити: а) закон зміни виробничої функції; б) ела+
стичність функції за кожним чинником; в) коефіцієнт еластичності
за чинниками при
х =
1,
у =
1
.
Розв’язок.
а) Щоб визначити зміну виробничої функції за чинниками
х
і
у
,
треба знати частинні похідні
дf
дx
та
дf
дy
.
дf
дx
= 20 + 8
х +
3
у
;
дf
дy
=
10 – 4
у
+ 3
х.
i
дy
дx
— гранична ефективність чинника
х
і
;
i
x
E
(
у
)
=
x
y
i
дy
дx
—
еластичність випуску
у
відносно чинника
х
і
.

363
Розділ V. Диференціальне числення функції багатьох змінних
б) Використавши означення еластичності функції за чинником,
знайдемо:
E
x
(
z
)
=
x
z
дz
дx
=
x
z
(20 + 8
x
+ 3
y
);
E
y
(
z
)
=
y
z
дz
дy
=
y
z
(10 – 4
y
+ 3
x
);
де
z =
20
х +
10
у –
2
у
2
+
4
х
2
+
3
ху
.
в) Обчислимо коефіцієнти еластичності при
х =
1,
у =
1.
Знайдемо спочатку значення виробничої функції при
х =
1,
у
= 1
.
E
x
(
z
)
=
20 8 3
35
=
31
35
|
0,89;
E
y
(
z
)
=
10 4 3
35
=
9
35
|
0,26.
Отже, із зростанням чинника
х
на 1% відбувається відносне зро+
стання заданої виробничої функції приблизно на 0,89% (за умови
стабільності чинника
у
). При зростанні чинника
у
на 1% і незмінності
чинника
х
виробнича функція зростає приблизно на 0,26%. Таким
чином, найбільше впливає на виробничу функцію
z = f
(
x
,
y
) чинник
х
.
Зауважимо, що від’ємне значення коефіцієнта еластичності по+
казує зменшення виробничої функції при зростанні відповідного
чинника. наприклад, якщо
E
x
(
z
) = –0,08 і
z = f
(
x
,
y
) — функція випус+
ку продукції, то зростання чинника
х
на 1% призводить до зниження
випуску продукції на 0,08%.
Приклад 5.71.
Нехай виробнича функція
z =
2
x
2
y
+ 3
xy
2
+ x
3
, де
х
— витрати живої праці,
у
— витрати уречевленої праці. Знайти
E
x
(
z
)
і
E
y
(
z
) в точці (1; 1).
Розв’язок.
Наближений відсотковий приріст функції
z
, що відпо+
відає приросту незалежних змінних
х
і
у
на 1%, визначимо за фор+
мулами:
E
x
(
z
)
=
x
z
дz
дx
та
E
y
(
z
)
=
y
z
дz
дy
.
Обчислимо частинні похідні функції
z
по
х
і по
у
:

364
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
дz
дx
=
4
ху +
3
у
2
+
3
х
2
;
дz
дy
=
2
х
2
+
6
ху
.
Тоді
E
x
(
z
)
=
22
223
(4 3 3 )
23
x
xy y x
x
yxyx
;
E
y
(
z
)
=
2
223
(2 6 )
23
y
xxy
x
yxyx
.
Знайдемо значення
E
x
(
z
) і
E
y
(
z
) в заданій точці (1; 1):
E
x
(
z
)
=
10
6
|
1,67;
E
y
(
z
)
=
8
6
|
1,33.
Із зростанням витрат живої праці на 1% обсяг виробництва
збільшиться приблизно на 1,67%, а із зростанням витрат уречевленої
праці на 1% обсяг виробництва збільшиться приблизно на 1,33%.
Приклад 5.72.
Фірма виробляє два види товарів
G
1
i
G
2
і продає
їх за ціною 1000 грош. од. та 800 грош. од відповідно. Обсяги випус+
ку товарів
Q
1
i
Q
2
. Функція витрат має вигляд:
С =
2
Q
1
2
+
2
Q
1
Q
2
+ Q
2
2
.
Знайти такі значення
Q
1
i
Q
2
, за яких прибуток, отриманий
фірмою, максимальний. Знайти цей прибуток.
Розв’язок.
Сумарний прибуток від продажу товарів
G
1
i
G
2
буде:
R =
1000
Q
1
+
800
Q
2
.
Прибуток, який отримає фірма, позначимо
П
. Він являє собою
різницю між прибутком
R
і витратами
С
, а саме:
П = R – C =
(1000
Q
1
+
800
Q
2
)
–
(2
Q
1
2
+
2
Q
1
Q
2
+ Q
2
2
);
П(Q
1
,
Q
2
)
=
1000
Q
1
+
800
Q
2
–
2
Q
1
2
–
2
Q
1
Q
2
– Q
2
2
.
Треба Знайти максимум цієї функції. Для знаходження стаціо+
нарних точок знаходимо частинні похідні першого порядку від
функції
П
(
Q
1
,
Q
2
) і прирівняємо їх до нуля:

365
Розділ V. Диференціальне числення функції багатьох змінних
1
дП
дQ
=
1000 – 4
Q
1
– 2
Q
2
,
2
дП
дQ
=
800 – 2
Q
1
– 2
Q
2
.
12
12
1000 4 2 0
800 2 2 0
QQ
QQ
®
¯
Розв’язавши систему, знайдемо
Q
1
= 100,
Q
2
= 300.
Отже, стаціонарна точка
М
0
(100; 300).
А =
2
2
1
дП
дQ
0
M
=
– 4;
В=
2
12
дП
дQ дQ
0
M
=
– 2;
С =
2
2
2
дП
дQ
0
M
= – 2.
А
< 0,
'
= AC – B
2
=
–4(–2) – 4 = 4 > 0
.
Тому точка
М
0
(100; 300) є точкою максимуму. Максимальний
прибуток досягається при обсягах виробництва
Q
1
= 100,
Q
2
= 300.
Знайдемо суму максимального прибутку:
П
(100; 300) = 1000
100 + 800
300 – 2
100
2
– 2100300 – 300
2
=
= 170000 грош. од.
В економічних дослідженнях часто ставиться задача порівняння
чинників і показника, прийнятого за функцію. У цьому випадку
доцільно залежність між функціональною ознакою і чинниками –
аргументами
х
1
,
х
2
, ... ,
х
р
виражати у вигляді степеневої функції
z = A
1
1
x
D
2
2
x
D
…
i
i
x
D
…
p
p
x
D
,
тоді показник степеня
i
D
є показником еластичності
z
по
х
і
. Наприк+
лад, обсяг виробництва в тисячах грошових одиниць в залежності від
деяких виробничих чинників
х
1
,
х
2
,
х
3
,
х
4
представлений функцією
z =
2,98(
х
1
)
0,39
(
х
2
)
0,48
(
х
3
)
0,18
(
х
4
)
–0,09
.
Коефіцієнти еластичності
1
D
= 0,39,
2
D
= 0,48,
3
D
= 0,18,
4
D
=
– 0,09
показують, що на темпи підвищення обсягу виробництва найбільше
впливає чинник
х
2
. У разі збільшення
х
2
на 1% випуск продукції
зростає на 0,48%. Збільшення ж
х
4
на 1% призводе до зниження ви+
пуску продукції на 0,09%.

366
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
5.4.2. Задачі для самостійного розв’язку
5.73.
Фірма реалізує частину товару на внутрішньому ринку, а
іншу частину поставляє на експорт. Зв’язок ціни товару
Р
1
і його
кількості
Q
1
, проданого на внутрішньому ринку, описується кривою
попиту за рівнянням
Р
1
+ Q
1
= 500
.
Аналогічно для експорту ціна
Р
2
і кількість
Q
2
також зв’язані співвідношенням (рівнянням кривої
попиту) 2
Р
1
+
3
Q
2
=
720. Сумарні витрати визначаються виразом
С
= 50000
+
20(
Q
1
+ Q
2
). Яку цінову політику повинна проводити
фірма, щоб прибуток був максимальним?
5.74.
Фірма виробляє два види товарів
G
1
i
G
2
в кількості
Q
1
і
Q
2
відповідно. Функція витрат має вигляд
С =
10
Q
1
+ Q
1
Q
2
+
10
Q
2
, а
криві попиту для кожного товару
Р
1
=
50 –
Q
1
+ Q
2
,
Р
2
= 30 + 2
Q
1
–
Q
2
,
де
Р
1
,
Р
2
— ціна одиниці товару видів
G
1
i
G
2
відповідно. Крім того,
фірма зв’язана обмеженнями на загальний обсяг виробництва товарів
G
1
i
G
2
, її квота складає 15
одиниць, тобто
Q
1
+ Q
2
= 15
.
Знайти мак+
симальний прибуток, що може бути досягнутий за цієї умови.
5.75.
Задана виробнича функція
z = z
(
x
,
y
), що дає залежність
між обсягом виробництва
z
і витратами живої праці
х
та уречевленої
праці
у
. Знайти: а)закон зміни виробничої функції за кожним із чин+
ників
х
та
у
; б) еластичність функції за кожним із чинників; в) кое+
фіцієнти еластичності по витратах живої та уречевленої праці при
х =
1,
у
= 1. Зробити висновки. Розв’язати задачу для наступних
функцій:
1)
z
(
x
,
y
)
= xy
3
–
3
x
2
y
3
+
2
y
4
–
120
y
;
2)
z =
ln(
x
3
+
2
y
3
);
3)
z = e
xy
;
4)
z
(
x
,
y
)
= –x
3
+
2
xy –
4
x –
8
y.
5.76.
На виробництві використовується два види ресурсів у
кількості
х
1
і
х
2
одиниць. Вартість одиниці кожного ресурсу складає
1 та 2 грош. од. Для придбання ресурсів виділено 10000 грош. од
.
Визначити оптимальні витрати ресурсів, що мають забезпечити
підприємству досягнення максимального прибутку, якщо відомо, що
сумарний прибуток
z
підприємства залежить від витрат ресурсів
наступним чином:
z =
2
x
1
+
10
x
2
– x
2
2
.

367
Розділ V. Диференціальне числення функції багатьох змінних
5.77.
Задана виробнича функція, що залежить від декількох
чинників:
z =
0,84(
x
1
)
0,624
(
х
2
)
–0,38
(
х
3
)
0,706
.
Провести аналіз впливу
відносних приростів чинників
х
1
,
х
2
,
х
3
на темпи зміни виробничої
функції.
5.78.
Фірма вирішила щомісяця асигнувати 100 тис. грош. од.
на виробництво деякої продукції. Середня заробітна платня по
фірмі складає 2000 грош.од.,
а вартість одиниці сировини дорів+
нює 1000 грош. од. Визначити, яку кількість робітників
R
і яку
кількість сировини
С
необхідно мати фірмі для отримання найб+
ільшого обсягу продукції
Q
, якщо відомо, що обсяг прямо про+
порційний кількості робітників і кількості сировини з коефіцієн+
том пропорційності 5.

368
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розділ VI. Інтегральне числення
§6.1. Первісна функція. Невизначений інтеграл.
Таблиця невизначених інтегралів
Знаходження функції
F
(
x
) по відомому її диференціалу
dF
(
x
)
= f
(
x
)
dx
(або по відомій її похідній
()
Fx
c
= f
(
x
))
,
тобто дія, обернена дифе+
ренціюванню, називається
інтегруванням
, а шукана функція
F
(
x
)
—
первісною функцією від заданої функції f(x)
.
Будь+яка неперервна функція
f
(
x
), має нескінчену множину
різних первісних функцій, які відрізняються одна від другої сталим
доданком: якщо
F
(
x
) є первісна від
f
(
x
), тобто якщо
()
Fx
c
= f
(
x
), то
і
F
(
x
)
+ С
, де
С
— довільна стала, є також первісна від
f
(
x
), так як
(() )
Fx C
c
=
()
Fx
c
= f
(
x
)
.
Загальний вираз
F
(
x
)
+ С
сукупності
всіх первісних від функції
f
(
x
) називається
невизначеним інтегра,
лом від цієї функції
і позначається знаком
:
³
()fxdx
³
= F
(
x
)
+ С
, якщо
d
(
F
(
x
)
+ С
)
= f
(
x
)
dx.
(6.1)
Властивості невизначеного інтеграла:
1.
() ()
x
fxdx fx
c
³
або
() ()d f xdx f xdx
³
.
(6.2)
2.
()Fxdx
c
³
= F(x) + С
або
()Fxdx
³
= F
(
x
)
+ С.
(6.3)
3.
()kf x dx
³
=
()kfxdx
³
, (6.4)
тобто сталий множник можна виносити за знак інтеграла.
4.
123
(() () ())fx fx fxdx
³
=
1
()fxdx
³
+
2
()fxdx
³
–
3
()fxdx
³
, (6.5)
тобто інтеграл від алгебраїчної суми дорівнює алгебраїчній сумі інтег+
ралів від всіх доданків.

369
Розділ VI. Інтегральне числення
6.1.1. Основні формули інтегрування
1.
n
vdv
³
=
1
1
n
v
n
+ C
,
1n z
.
1.
c
dv
³
= v + C
.
2.
dv
v
³
=
ln
|v| + C.
3.
sin vdv
³
= –
cos
v + C
.
4.
cos vdv
³
= sin
v + C.
5.
2
cos
dv
v
³
=
tg
v + C
.
6.
2
sin
dv
v
³
= –
ctg
v + C.
7.
tg vdv
³
=
– ln
|
cos
v| + C.
8.
tgcvdv
³
=
ln
|
sin
v| + C.
9.
v
adv
³
=
ln
v
a
a
+ C.
9.
c
v
edv
³
= e
v
+ C.
10.
22
dv
va
³
=
1
a
arctg
v
a
+ C.
11.
22
dv
va
³
=
1
2a
ln
va
va
+ C.
11 .
c
22
dv
av
³
=
1
2a
ln
av
av
+ C.
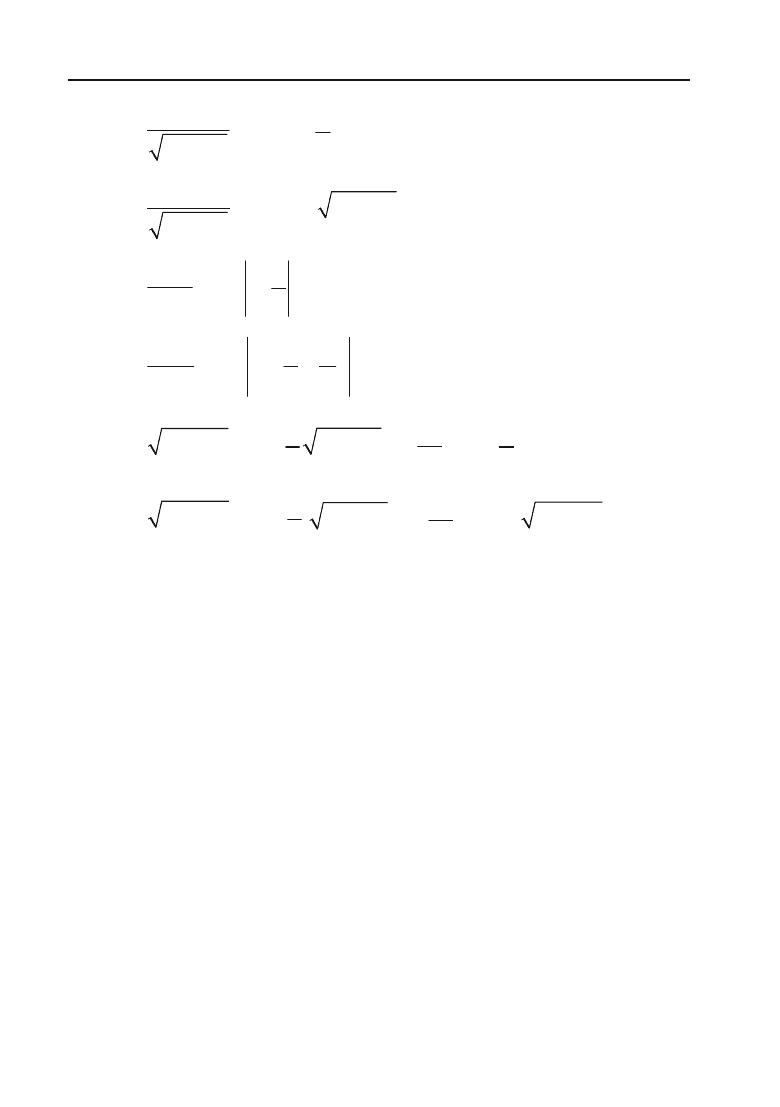
370
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
12.
22
dv
av
³
=
arcsin
v
a
+ C.
13.
22
dv
var
³
=
ln
|
22
vvar
| + C.
14.
sin
dv
v
³
=
ln
tg
2
v
+ C.
15.
cos
dv
v
³
=
ln
tg
24
v
S
§·
¨¸
©¹
+ C.
16.
22
avdv
³
=
22
2
v
av
+
2
2
a
arcsin
v
a
+ C.
17.
22
vadvr
³
=
2
v
22
var
r
2
2
a
ln
|
22
vvar
| + C.
В цих формулах
а
— стала,
v
— незалежна змінна або будь+яка
(диференційовна) функція від незалежної змінної.
