Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

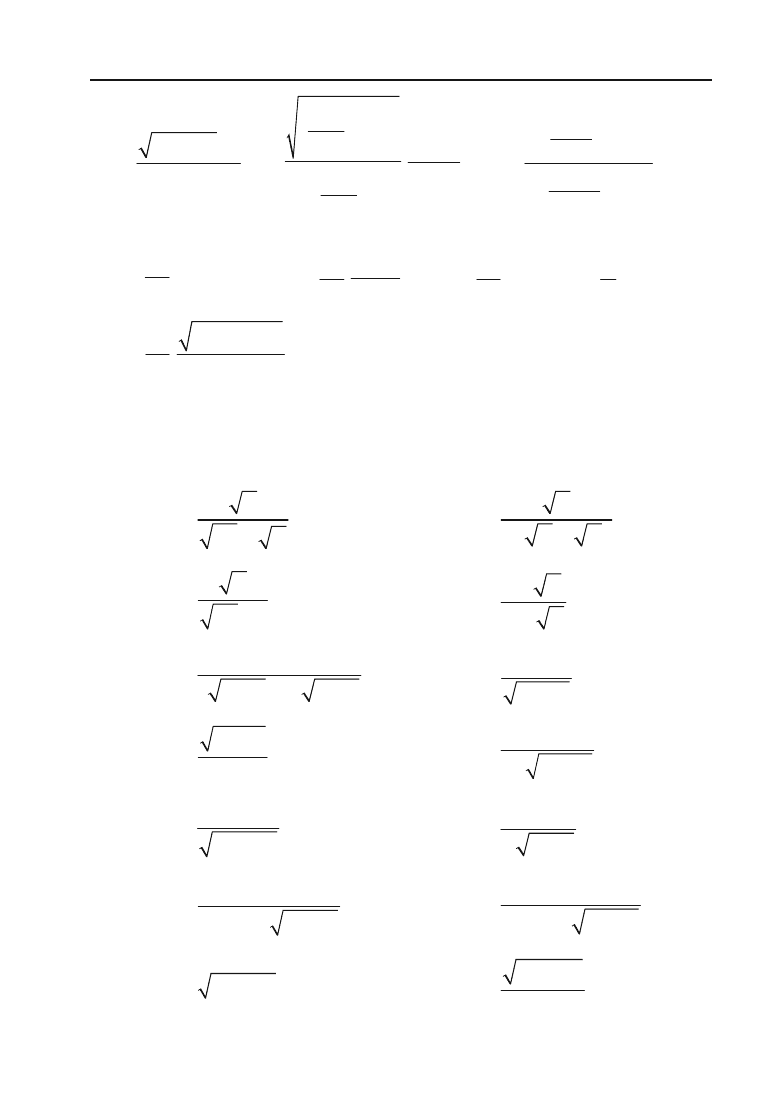
411
Розділ VI. Інтегральне числення
2
4
25xdx
x
³
=
2
4
5
25
cos
5
cos
t
t
§·
¨¸
©¹
§·
¨¸
©¹
³
2
5sin
cos
t
t
dt =
2
42
4
sin
5sin
cos
1
5cos
cos
t
tdt
t
t
t
³
=
=
1
25
2
sin costtdt
³
=
1
25
3
sin
3
t
+ C =
1
75
sin
3
(arccos
5
x
) + C =
=
1
75
23
3
(25)x
x
+ C.
6.5.4. Приклади для самостійного розв’язку
Знайти інтеграли:
6.158.
3
23
x
dx
xx
³
. 6.159.
3
3
()
x
dx
xx x
³
.
6.160.
3
4
1
x
dx
x
³
. 6.161.
4
1 x
dx
xx
³
.
6.162.
4
(31)3
dx
xx
³
. 6.163.
1
21
x
dx
x
³
.
6.164.
2
4
1 x
dx
x
³
. 6.165.
22
9
dx
xx
³
.
6.166.
2
2
25
xdx
x
³
. 6.167.
3
8
dx
xx
³
.
6.168.
2
22
(4 ) 4
xdx
xx
³
. 6.169.
22
(9 ) 9
dx
xx
³
.
6.170.
2
16 xdx
³
. 6.171.
2
4
36x
dx
x
³
.

412
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§ 6.6. Визначений інтеграл. Властивості визначеного
інтеграла. Формула НьютонаAЛейбтіца
Якщо функція f(x) неперервна на відрізку [a; b] (де а < b), і якщо:
1) розбити цей відрізок довільним чином на n частинних відрізків
довжиною
1
x
'
,
2
x
'
, ...,
n
x
'
;
2) вибрати на кожному частинному відрізку по одній довільній
точці
1
H
,
2
H
, ...,
n
H
;
3) обчислити значення функції f(x) у вибраних точках;
4) скласти суму
f(
1
H
)
1
x
'
+ f(
2
H
)
2
x
'
+ ... + f(
n
H
)
n
x
'
=
1
()
n
ii
i
f
x
H
'
¦
,
то вона називається інтегральною сумою f(x) на відрізку [a; b].
Якщо по різному ділити відрізок [a; b] на n частинних відрізків і
по+різному вибирати на них по одній точці
i
H
, то можна для будь+
якої неперервної заданої функції f(x) і будь+якого заданого відрізка
[a; b] скласти нескінчену множину різних інтегральних сум. При
цьому виявляється, що всі ці різні інтегральні суми при необмеже+
ному зростанні n при прямуванні до нуля найбільшої із довжин ча+
стинного відрізка, мають одну і ту ж границю. Ця границя всіх інтег+
ральних сум функції f(x) на відрізку [a; b] називається
визначеним
інтегралом від f(x) в межах від а до b
та позначається
()
b
a
fxdx
³
.
6.6.1. Найпростіші властивості визначеного інтеграла
1. При перестановці меж інтегрування знак інтегралу змінюється
на протилежний:
()
b
a
fxdx
³
= – ()
a
b
f
xdx
³
. (6.23)

413
Розділ VI. Інтегральне числення
2. Інтеграл з однаковими межами дорівнює нулю:
()
a
a
fxdx
³
= 0.
3. Відрізок інтегрування можна розбити на частини:
()
b
a
fxdx
³
=
()
c
a
fxdx
³
+ ()
b
c
f
xdx
³
. (6.24)
4. Інтеграл від алгебраїчної суми функцій дорівнює сумі інтег+
ралів від кожного доданку:
123
(() () ())
b
a
f
xfxfxdx
³
=
1
()
b
a
f
xdx
³
+
2
()
b
a
f
xdx
³
–
3
()
b
a
f
xdx
³
. (6.25)
5. Постійний множник k можна виносити за знак інтеграла:
()
b
a
kf x dx
³
= k
()
b
a
f
xdx
³
. (6.26)
6. Якщо функція y = f(x) неперервна на відрізку [a; b] (де a < b),
то знайдеться таке значення
[
[a; b], що виконується рівність:
()
b
a
f
xdx
³
= f(
[
)(b – a) (теорема про середнє). (6.27)
Для обчислення визначеного інтеграла, коли можна знайти
відповідний невизначений інтеграл, служить формула Ньютона+
Лейбніца:
()
b
a
fxdx
³
= F(x)
b
a
= F(b) – F(a), (6.28)
— визначений інтеграл дорівнює різниці значень невизначеного інтег+
рала при верхній та нижній межах інтегрування.
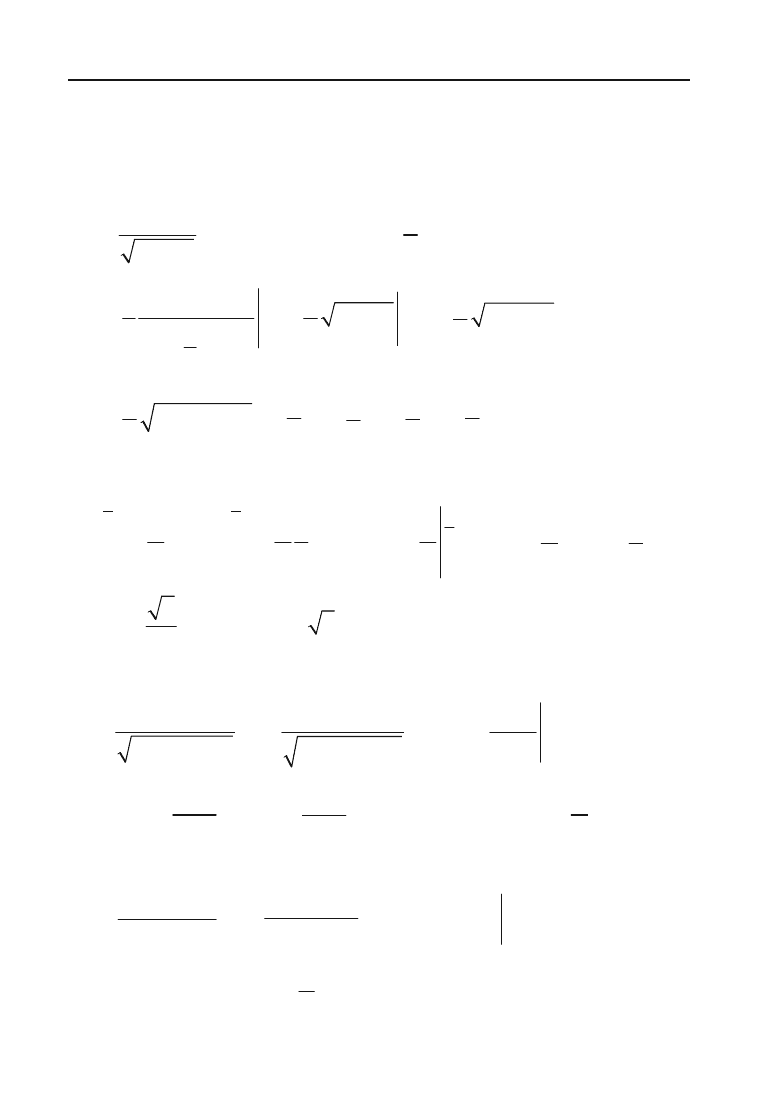
414
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.6.2. Розв’язання прикладів
Обчислити інтеграли.
Приклад 6.172.
7
1
34
dx
x
³
=
7
1/2
1
(3 4)xdx
³
=
7
1/2
1
1
(
34
)
3
3
x
dx
³
=
=
1/2 1
7
1
1(3 4)
1
3
1
2
x
=
7
1
2
34
3
x
=
2
37 4
3
–
–
2
3(1) 4
3
=
2
3
5 –
2
3
1 =
8
3
= 2
2
3
.
Приклад 6.173.
2
0
sin
2
x
dx
S
³
= 2
2
0
1
sin
22
x
dx
S
³
= –2cos
2
0
2
x
S
= –2cos
4
S
+ 2cos
0
2
=
= –2
2
2
+ 2
1 = 2 –
2
.
Приклад 6.174.
5
2
2
54
dx
xx
³
=
5
2
2
9( 2)
dx
x
³
= arcsin
5
2
2
3
x
=
= arcsin
52
3
– arcsin
22
3
= arcsin 1 – arcsin 0 =
2
S
.
Приклад 6.175.
0
2
1
22
dx
xx
³
=
0
2
1
(
1
)
1
dx
x
³
= arctg(x + 1)
0
1
=
= arctg 1 – arctg 0 =
4
S
.
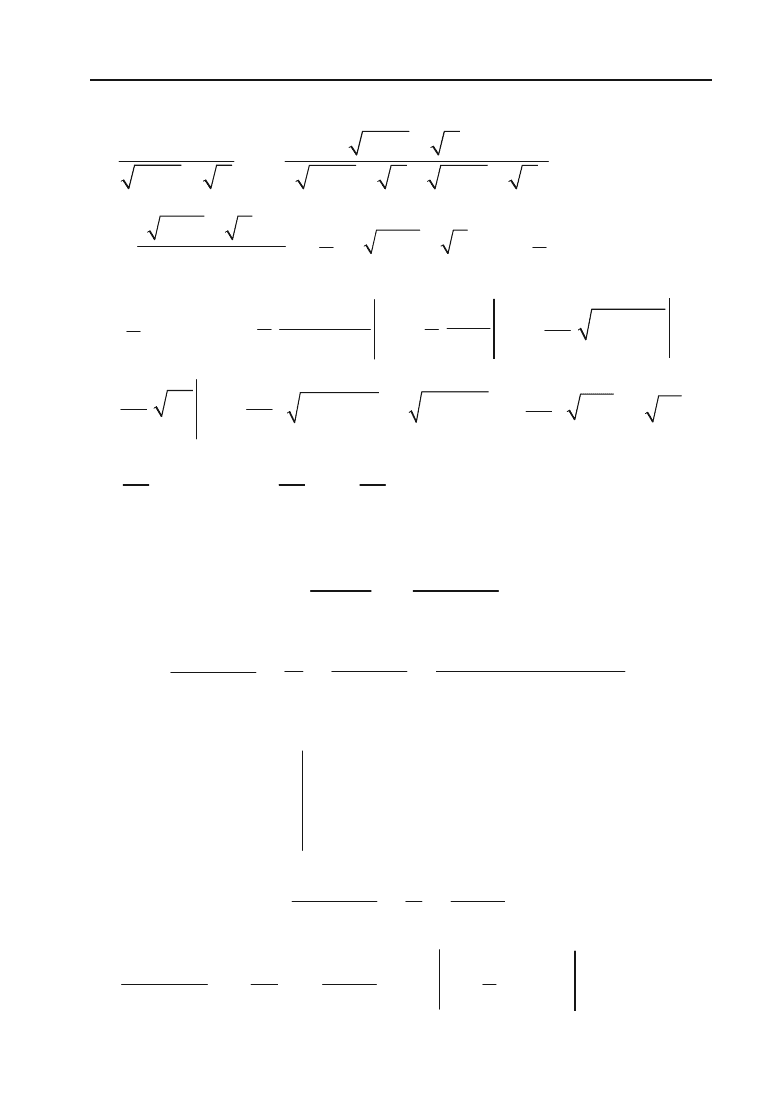
415
Розділ VI. Інтегральне числення
Приклад 6.176.
16
0
9
dx
xx
³
=
16
0
(9)
(9)(9)
xxdx
x
xx x
³
=
=
16
0
(9)
9
xxdx
xx
³
=
1
9
16
0
(9)xxdx
³
=
1
9
16
1/2
0
(9)xdx
³
+
+
1
9
16
1/2
0
xdx
³
=
1
9
3/2
16
0
(9)
3/2
x
+
1
9
3/2
16
0
3/2
x
=
2
27
3
16
0
(9)x
+
+
2
27
3
16
0
x
=
2
27
(
3
(
16 9
)
–
3
(0 9)
) +
2
27
(
3
16
–
3
0
) =
=
2
27
(125 – 27) +
2
27
64 =
2
27
162 = 12.
Приклад 6.177.
2
3
1
dx
xx
³
=
2
2
1
(1 )
dx
xx
³
;
2
1
(1 )xx
=
A
x
+
2
1
Mx N
x
=
22
2
(1 )
A
Ax Mx Nx
xx
;
A + Ax
2
+ Mx
2
+ Nx = 1;
2
0
x
x
x
0
0
1
AM
N
A
½
°
¾
°
¿
1,
0,
1.
M
N
A
2
1
(1 )
x
x
=
1
x
–
2
1
x
x
;
2
2
1
(1 )
dx
xx
³
=
2
1
dx
x
³
–
2
2
1
1
x
dx
x
³
= ln|x|
2
1
–
1
2
ln|1+ x
2
|
2
1
= ln2 – ln1 –

416
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.6.3. Приклади для самостійного розв’язання
Обчислити інтеграли.
6.178.
3
32
2
(2 5)
xx dx
³
. 6.179.
2
3
2
(4)
xxdx
³
.
6.180.
1
3
2
(
11 5
)
dx
x
³
. 6.181.
13
4
5
2
(3 )
dx
x
³
.
6.182.
9
4
1
1
y
dy
y
³
. 6.183.
1
2
0
45
dx
xx
³
.
6.184.
3
2
2
1
xdx
x
³
. 6.185.
4
6
2
cos
dx
x
S
S
³
.
6.186.
2
2
0
3
4
x
dx
x
³
. 6.187.
2
2
1
54
dx
xx
³
.
6.188.
0
sin cos
22
xx
dx
S
³
. 6.189.
0
3
cos cos
22
xx
dx
S
³
.
6.190.
1
2
0,5
82
dx
xx
³
. 6.191.
31
2
0
32
dx
x
x
³
.
6.192.
2
2
1cos
dx
x
S
S
³
. 6.193.
2
2
1
1
sin
dx
x
x
S
S
³
.
–
1
2
ln5 +
1
2
ln2 =
3
2
ln2 –
1
2
ln5 =
1
2
(ln8 – ln5) =
1
2
ln
8
5
.

417
Розділ VI. Інтегральне числення
6.194.
4
2
0
sin
cos
x
dx
x
S
³
. 6.195.
2
2
0
sin 2
xdx
S
³
.
6.196.
2
3
2
cos cos
x
xdx
S
S
³
. 6.197.
3
2
2
232
dx
xx
³
.
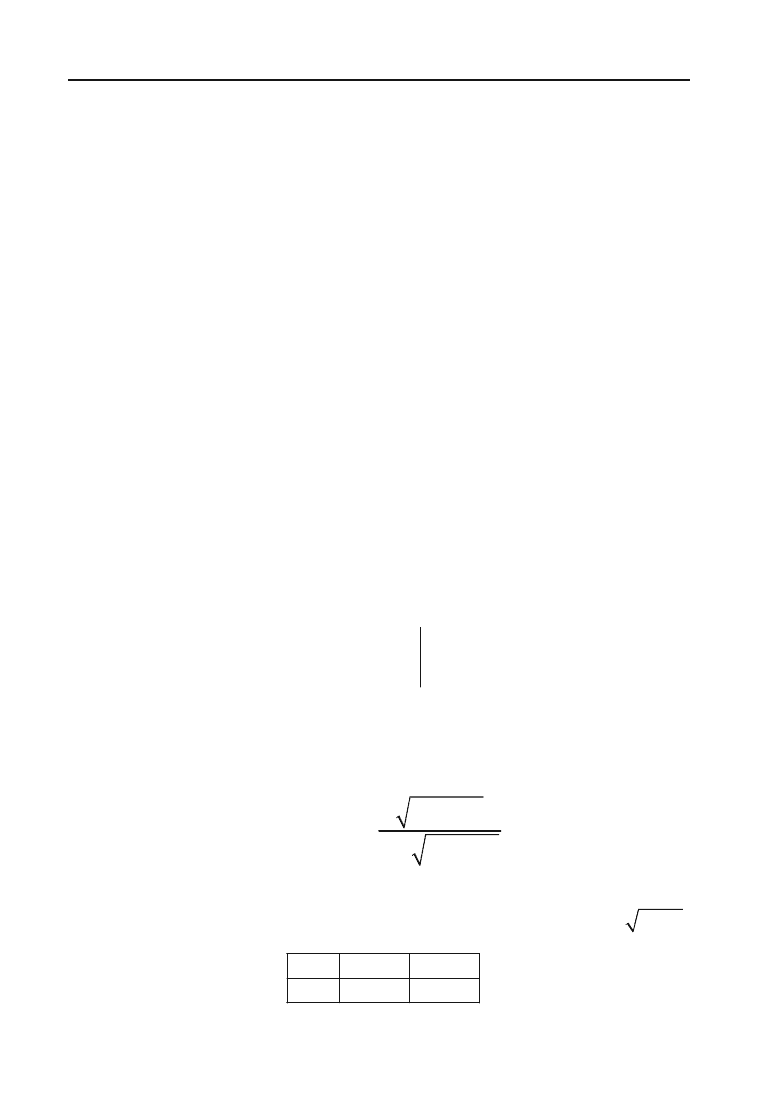
418
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.7.1. Розв’язання прикладів
Приклад 6.198. Обчислити
29
2
3
2
3
3
(2)
3(2)
x
dx
x
³
.
Розв’язок. Введемо підстановку x – 2 = t
3
, x = t
3
+ 2, dx = 3t
2
dt.
Знайдемо нові межі інтегрування, використовуючи рівняння t =
3
2x
:
§ 6.7. Методи підстановки та інтегрування частинами
у визначеному інтегралі
Для обчислення багатьох визначених інтегралів необхідно замі+
няти змінну інтегрування. При цьому, якщо визначений інтеграл
()
b
a
f
xdx
³
перетворюється за допомогою підстановки x =
()
t
M
в
інший інтеграл, з новою змінною t, то задані межі x
1
= a i x
2
= b
заміняються новими межами t
1
=
D
i t
2
=
E
, які визначаються із
вибраної підстановки, тобто із рівнянь a =
()
M
D
, b =
()
M
E
. Якщо
()t
M
c
і
(())
f
t
M
неперервні та відрізку [
D
;
E
], то
()
b
a
fxdx
³
=
(()) ()
ft tdt
E
D
MM
c
³
. (6.29)
Якщо підінтегральний вираз у визначеному інтегралі можна пред+
ставити в вигляді добутку двох співмножників u та dv, то для обчис+
лення визначеного інтегралу необхідно скористатися формулою інтег+
рування частинами у визначеному інтегралі:
b
a
udv
³
= uv
b
a
–
b
a
vdu
³
. (6.30)
x 3 29
t 1 3
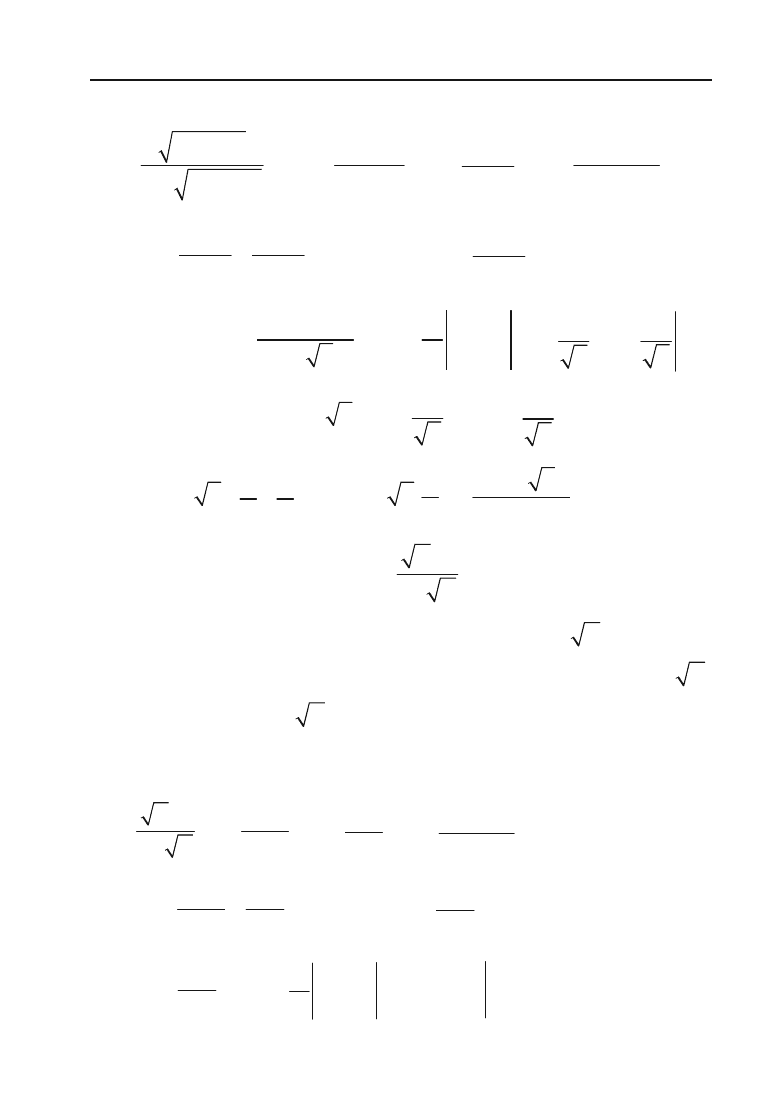
419
Розділ VI. Інтегральне числення
Одержуємо
29
2
3
2
3
3
(2)
3(2)
x
dx
x
³
=
3
22
2
1
3
3
ttdt
t
³
= 3
3
4
2
1
3
tdt
t
³
= 3
3
4
2
1
99
3
t
dt
t
³
=
= 3
3
4
22
1
99
33
t
dt
tt
§·
¨¸
©¹
³
= 3
3
2
2
1
9
(
3
)
3
tdt
t
³
= 3
3
2
1
tdt
³
–
– 9
3
1
dt
³
+ 27
3
22
1
9
(3)
dt
t
³
= 3
3
3
31
t
– 9t
3
1
+
27
3
arctg
3
1
3
t
=
= 27 – 1 – 27 + 9 + 9
3
(аrctg
3
3
– arctg
1
3
) =
= 8 + 9
3
36
SS
§·
¨¸
©¹
= 8 + 9
3
6
S
=
16 3 3
2
S
.
Приклад 6.199. Обчислити
4
1
1
xdx
x
³
.
Розв’язок. Введемо підстановку x = t
2
, dx = 2tdt,
x
= t.
Знайдемо нові межи інтегрування використовуючи рівність t =
x
.
Спочатку в рівність t =
x
підставимо нижню межу інтегрування х = 1,
а потім верхню х = 4, і одержуємо: при х = 1
t = 1; при x = 4
t = 2. Нові межі інтегрування 1
d
t
d
2. Переходимо до обчислення:
4
1
1
xdx
x
³
=
2
1
2
1
ttdt
t
³
= 2
2
2
1
1
tdt
t
³
= 2
2
2
1
11
1
t
dt
t
³
=
= 2
2
2
1
11
11
t
dt
tt
§·
¨¸
©¹
³
= 2
2
1
1
1
1
tdt
t
§·
¨¸
©¹
³
= 2
2
1
tdt
³
– 2
2
1
dt
³
+
+ 2
2
1
1
1
dt
t
§·
¨¸
©¹
³
= 2
2
2
21
t
– 2t
2
1
+ 2ln|t+1|
2
1
= 4 – 1 – 4 + 2 +
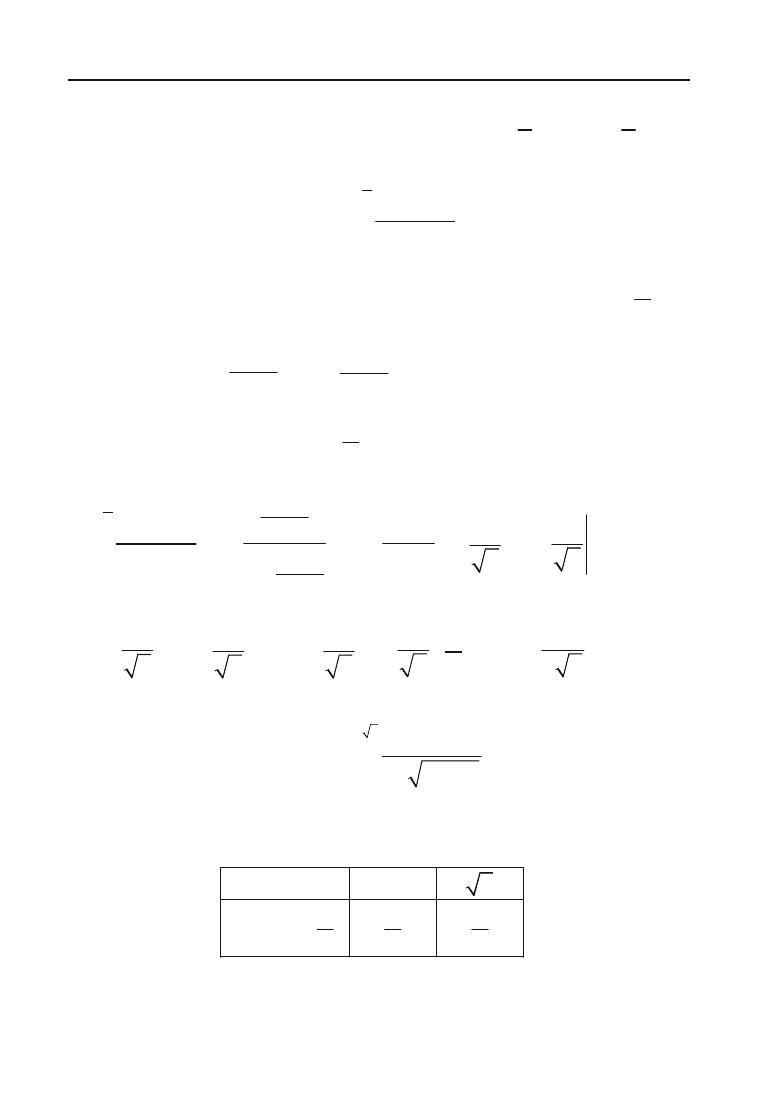
420
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
+ 2ln 3 – 2ln 2 = 1 + 2(ln 3 – ln 2) = 1 + 2ln
3
2
= 1 + ln
9
4
.
Приклад 6.200. Обчислити
2
0
2cos
dx
x
S
³
.
Розв’язок. Замінюючи змінну за допомогою підстановки tg
2
x
= t,
знайдемо cos x =
2
2
1
1
t
t
, dx =
2
2
1
dt
t
, та нові межі інтегрування t
1
= 0
при x
1
= 0, та t
2
= 1 при х
2
=
2
S
.
2
0
2cos
dx
x
S
³
=
1
2
2
0
2
2
1
1
2
1
dt
t
t
t
³
= 2
1
2
0
3
dt
t
³
=
2
3
arctg
1
0
3
t
=
=
2
3
(arctg
1
3
– arctg
0
3
) =
2
3
(
6
S
– 0) =
33
S
.
Приклад 6.201. Обчислити
3
3
22
1
(1)
4
x
dx
x
x
³
.
Розв’язок. Введемо підстановку x = 2sin t. Одержуємо dx = 2cos tdt,
та нові межі інтегрування:
x 1
3
t = arcsin
2
x
6
S
3
S
