Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


451
Розділ VI. Інтегральне числення
За першою формулою прямокутників (4.43) одержуємо:
2
1
dx
x
³
|
0,1(у
0
+ у
1
+ ... + у
9
) = 0,1
7,1877 = 0,71877.
За другою формулою прямокутників (6.43) одержуємо:
2
1
dx
x
³
|
0,1(у
1
+ у
2
+ у
3
+ ... + у
10
) = 0,1
6,68773 = 0,66877.
За формулою трапеції (6.44) одержуємо:
2
1
dx
x
³
|
0,1(
10,5
2
+ 6,18773) = 0,69377.
За формулою Сімпсона (6.45) маємо:
2
1
dx
x
³
|
0,1
3
(у
0
+ у
10
+ 2(у
2
+ у
4
+ у
6
+ y
8
) + 4(y
1
+ y
3
+ у
5
+ y
7
+ у
9
) =
=
0,1
3
(1
0,5 + 2
2,72818 + 43,45955) = 0,6931.
В дійсності
ln 2
=
2
1
dx
x
³
= 0,6931472 (з точністю до сьомого знаку).
Таким чином, при поділі відрізка [0; 1] на 10 частин за форму+
лою Сімпсона ми одержали п’ять вірних знаків; за формулою тра+
пецій — лише три вірних знака; а за формулою прямокутника ми
можемо ручатися тільки за перший знак.
x
1
y
x
x
1
y
x
x
0
= 1,0 y
0
= 1,0000 x
6
= 1,6 y
6
= 0,62500
x
1
= 1,1 y
1
= 0,90909 x
7
= 1,7 y
7
= 0,58824
x
2
= 1,2 y
2
= 0,83333 x
8
= 1,8 y
8
= 0,55556
x
3
= 1,3 y
3
= 0,76923 x
9
= 1,9 y
9
= 0,52632
x
4
= 1,4 y
4
= 0,71429 x
10
= 2,0 y
10
= 0,5000
x
5
= 1,5 y
5
= 0,66667

452
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.10.5. Приклади для самостійного розв’язання
Знайти наближене значення інтегралів методами трапецій і
Сімпсона.
6.286.
1,7
0,1
dx
x
³
.
6.287.
1
0
arctg x
dx
x
³
.
Знайти наближене значення інтеграла методом Сімпсона.
6.288.
2
1
0
x
edx
³
.

453
Розділ VI. Інтегральне числення
§ 6.11. Невласні інтеграли. Інтеграл ЕйлераAПуассона
6.11.1. Поняття і різновиди власних інтегралів
Згідно з теоремою існування визначеного інтеграла цей інтеграл
існує, якщо виконані умови:
1) відрізок інтегрування [
a; b] скінчений;
2) підінтегральна функція
f(x) неперервна або обмежена і має
скінчену кількість точок розриву.
Якщо хоч би одна із цих умов не виконується, то визначений
інтеграл називають невласним. Якщо не виконується перша умова,
тобто
b =
f
; або а =
f
; або а =
f
і b =
f
, то інтеграли назива+
ють
невласними інтегралами з нескінченими межами. Якщо не вико+
нується лише друга умова, то підінтегральна функція
f(x) має точки
розриву на відрізку [
a; b]. В цьому випадку
()
b
a
fxdx
³
називають не
власним інтегралом від розривної функції, необмеженої в точках
відрізку інтегрування
.
6.11.2. Дослідження невласних інтегралів
Дослідження невласних інтегралів проводять шляхом викорис+
тання граничного переходу у визначеному інтегралі.
Інтеграли з необмеженими межами визначають так:
()
a
f
xdx
f
³
=
lim ( )
b
b
a
fxdx
of
³
;
()
b
fxdx
f
³
=
lim ( )
b
a
a
fxdx
of
³
;
()
f
xdx
f
f
³
=
()
c
f
xdx
f
³
+
()
c
f
xdx
f
³
=
lim ( )
c
a
a
f
xdx
of
³
+
lim ( )
b
b
c
f
xdx
of
³
.
Якщо вказані границі існують (будуть скінченими числами), то
відповідний інтеграл називають
збіжним, і він дорівнює своїй гра+
ниці. Якщо якась границя не існує або дорівнює нескінченності, то
інтеграл називають
розбіжним.
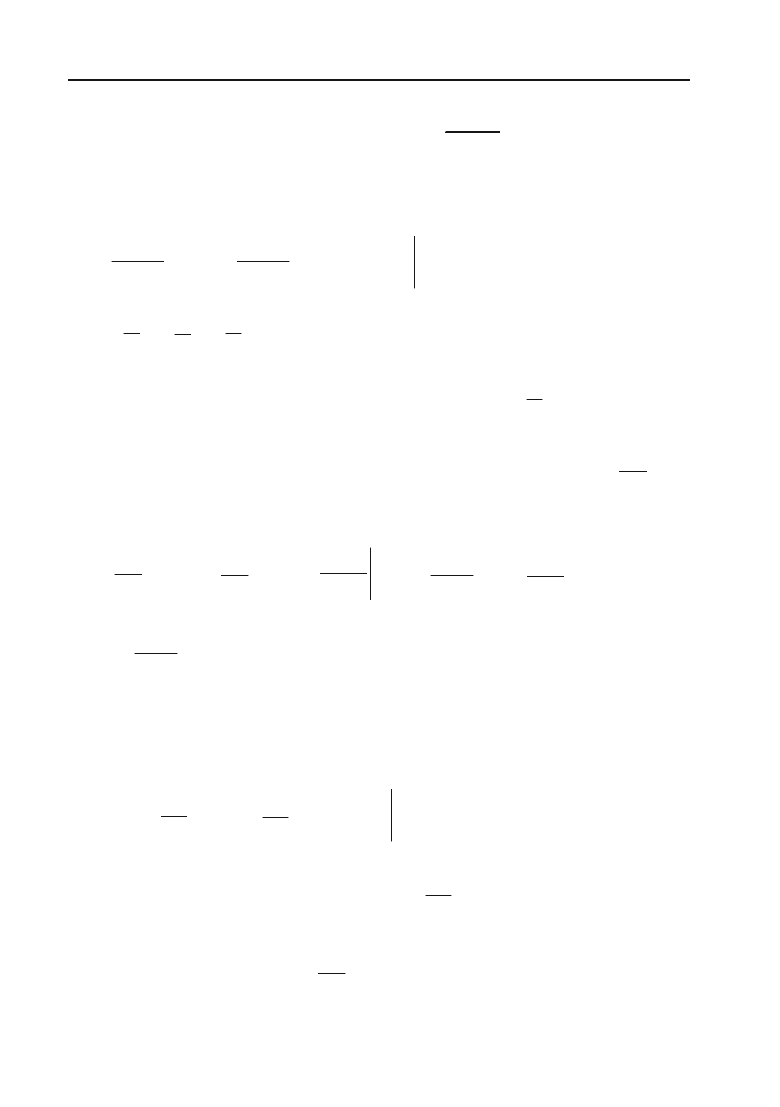
454
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 6.289. Обчислити інтеграл
2
1
1
dx
x
f
³
або встановити його
розбіжність.
Розв’язок. Згідно з означенням невласного інтеграла маємо:
2
1
1
dx
x
f
³
=
2
1
lim
1
b
b
dx
x
of
³
=
lim
bof
arctg x
1
b
=
lim
bof
(arctg b – arctg 1) =
=
2
S
–
4
S
=
4
S
.
Отже, цей інтеграл існує, збіжний і дорівнює
4
S
.
Приклад 6.290. Встановити збіжність або розбіжність
1
p
dx
x
f
³
.
Розв’язок. Згідно з означенням невласного інтеграла маємо:
1
p
dx
x
f
³
=
1
lim
b
p
b
dx
x
of
³
=
lim
bof
1
1
1
p
b
x
p
= –
1
1
p
(
lim
b
of
1
1
p
b
– 1) =
=
1
, 1
1
, 1
p
p
p
!
°
®
°
f
¯
.
Отже, при р > 1 інтеграл збіжний, а при p < 1 — розбіжний.
Розглянемо випадок
р = 1.
1
dx
x
f
³
=
1
lim
b
b
dx
x
of
³
=
lim
bof
ln|x|
1
b
=
lim
bof
ln b + ln 1 =
f
.
Таким чином, при
р = 1 інтеграл
1
dx
x
f
³
— розбіжний.
Одержали, що інтеграл
1
p
dx
x
f
³
збіжний при p>1, і розбіжний при p
d
1.

455
Розділ VI. Інтегральне числення
Приклад 6.291. Обчислити
x
edx
f
f
³
або встановити його роз+
біжність.
Розв’язок. Дослідимо на збіжність інтеграли
0
x
edx
f
³
і
0
x
edx
f
³
.
0
x
edx
f
³
=
0
lim
x
a
a
edx
of
³
=
lim
aof
е
х
0
a
=
lim
aof
(е
0
– е
а
) = 1,
тобто, перший інтеграл збігається до 1.
Але
0
x
edx
f
³
=
lim
bof
0
b
x
edx
³
=
lim
bof
(е
b
– 1) =
f
,
тобто
0
x
edx
f
³
є розбіжним. Отже, і інтеграл
x
edx
f
f
³
є розбіжним.
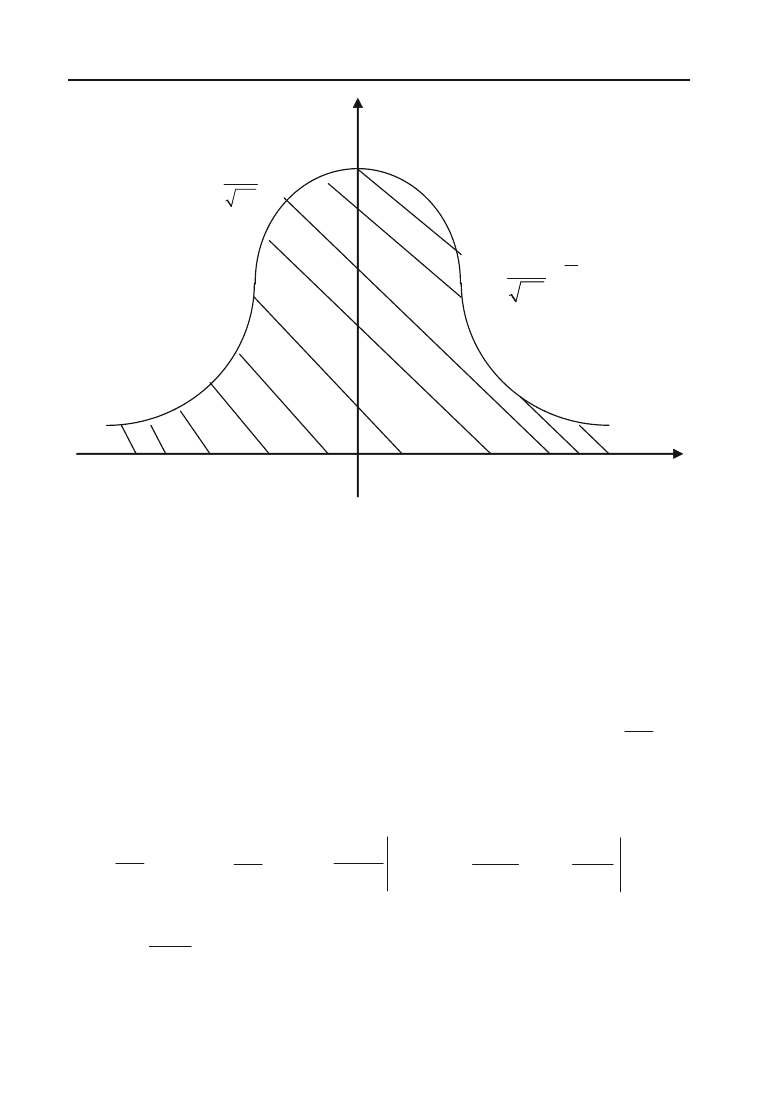
В курсі теорії ймовірностей зустрічається невласний інтеграл
2
2
x
edx
f
f
³
, що називається інтегралом ЕйлераПуассона. Доведено, що
2
2
x
edx
f
f
³
=
2
S
, іншими словами площа S під кривою Гаусса
2
2
1
2
x
y
e
S
на інтервалі (
f
;
f
) дорівнює 1 (див. рис. 6.14).
У випадку необмеженої на [
a; b] функції f(x) її точки розриву
можуть бути на лівому кінці або на правому кінці, або в середині
проміжку інтегрування [
a; b]. У цих випадках невласні інтеграли
визначаються так:
()
b
a
fxdx
³
=
0
lim ( )
bе
е
a
f
xdx
o
³
;
()
b
а
f
xdx
³
=
0
lim
()
b
е
aе
f
xdx
o
³
;
456
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
()
и
а
f
xdx
³
=
'
'0
lim
()
cе
е
a
f
xdx
o
³
+
'' 0
''
lim ( )
b
е
cе
fxdx
o
³
.
Якщо вказані границі існують, то відповідний інтеграл назива+
ють
збіжним. У протилежному випадку інтеграл називають розбіж
ним.
Приклад 6.292. Встановити збіжність, або розбіжність
1
0
p
dx
x
³
.
Розв’язок. Функція необмежена при x = 0. Згідно з означенням
невласного інтеграла маємо:
1
0
p
dx
x
³
=
1
0
0
lim
p
е
е
dx
x
o
³
=
0
lim
е
o
1
1
0
1
p
е
x
p
=
1
1p
(
0
lim
е
o
1
1
p
х
1
0 е
) =
=
1
, 1
1
, 1
p
p
p
°
®
°
f t
¯
.
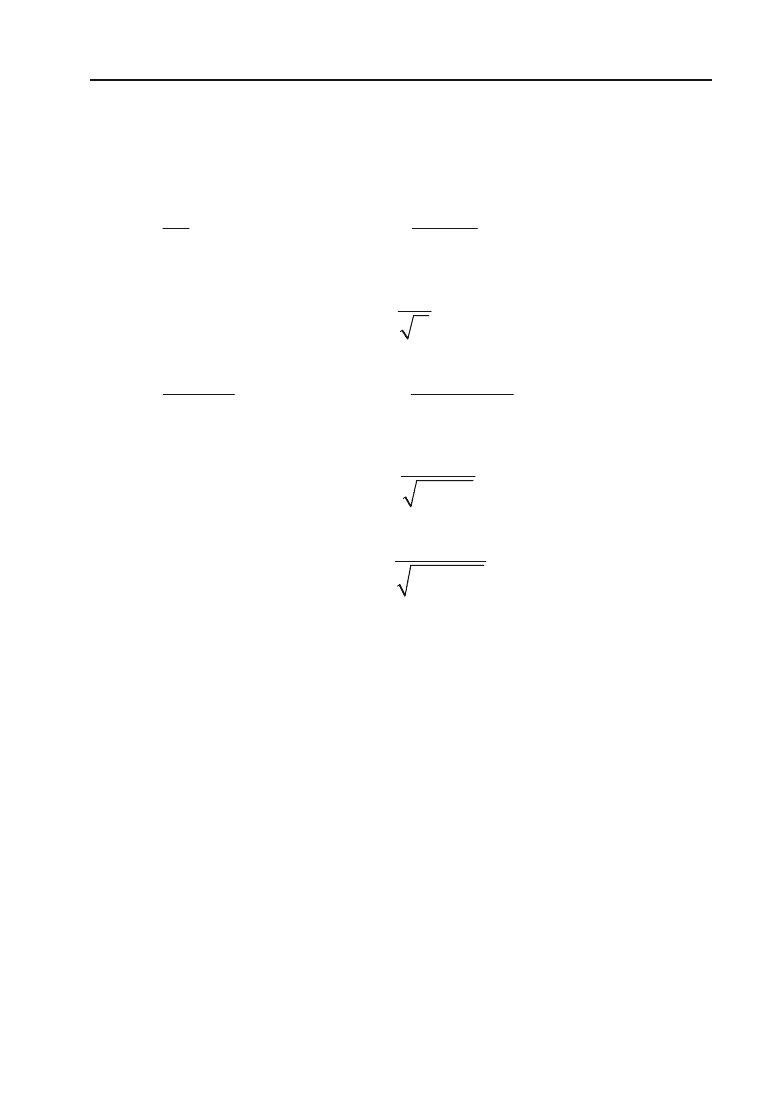
S = 1
1
2
S
Y
2
2
1
2
x
ye
S
0 X
Рис.6.14.
457
Розділ VI. Інтегральне числення
6.11.3. Приклади для самостійного розв’язку
6.294. Обчислити невласні інтеграли (або встановити їх розбіж+
ність):
а)
3
1
dx
x
f
³
;б)
1/2
2
0
ln
dx
xx
³
;
в)
2
0
x
edx
f
³
;г)
1
3
0
dx
x
³
;
д)
3
2
0
(1)
dx
x
³
;ж)
2
22
dx
xx
f
f
³
;
з)
1
0
ln xdx
³
;и)
3
2
3
2
4
x
dx
x
³
;
і)
0
x
xe dx
f
³
;ї)
6
2
3
2
(5 )
dx
x
³
.
458
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§ 6.12. Поняття про подвійний інтеграл
Подвійним інтегралом від функції f(x, y) по області
V
нази+
вається границя, до якої прямує інтегральна сума
1
(,)
n
ii i
i
fxy
V
'
¦
при необмеженому зростанні числа малих площадок
i
V
'
та при
умові, що кожна з них стягується в точку.
6.12.1. Обчислення подвійного інтеграла
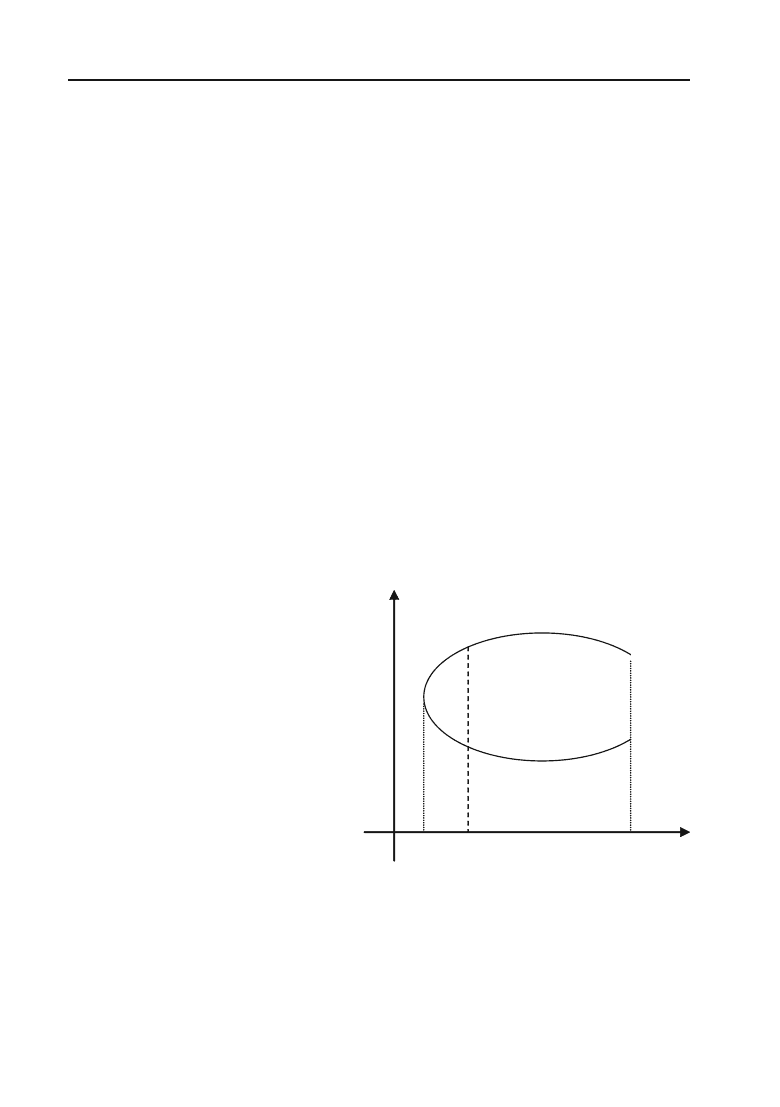
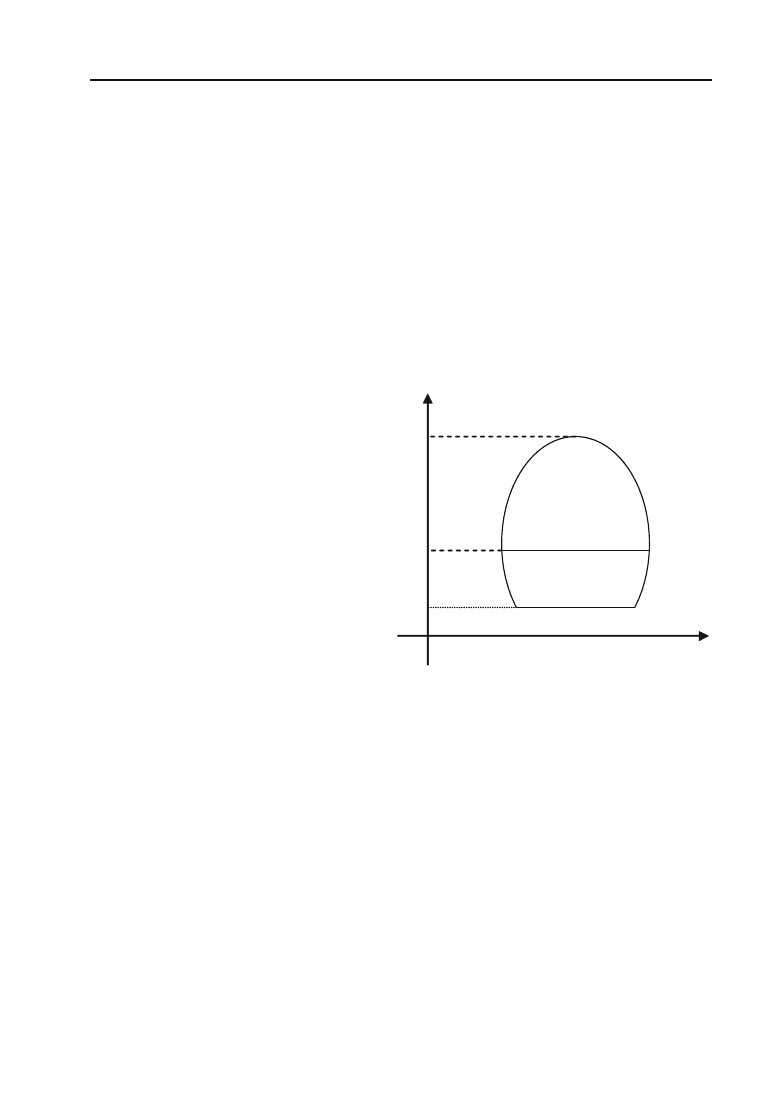
1. Якщо область інтегрування
V
обмежена кривою, яку будь+яка
пряма, що паралельна осі
Оу, перетинає не більше ніж в двох точках
(рис. 6.15), то подвійний інтеграл області
V
обчислюється за фор+
мулою:
(,)
f
xydxdy
V
³³
=
2
1
()
()
(,)
x
b
ax
dx f x y dy
M
M
³³
. (6.46)
Інтеграл в правій частині
цієї формули називається по+
вторним. В формулі (6.46)
інтеграл
2
1
()
()
(,)
x
x
f
xydy
M
M
³
нази+
вається
внутрішнім. Тут межі
інтегрування є функції змінної
х. При обчисленні внутрішнь+
ого інтегралу в підінтегральній
функції потрібно
х розглядати
як величину сталу, а
у —
змінну. В результаті першого
(внутрішнього) інтегрування одержуємо функцію аргументу
х. Після
того, як ця функція визначена
2
1
()
()
() (,)
x
x
Фx f xydy
M
M
³
, необхідно ви+
Рис. 6.15.
0 а х b X
1
()yx
M
K
L
2
()yx
M
Y
V
459
Розділ VI. Інтегральне числення
конати зовнішнє (друге) інтегрування
()
b
a
Фxdx
³
. В результаті цього
другого інтегрування одержуємо уже не функцію, а число.
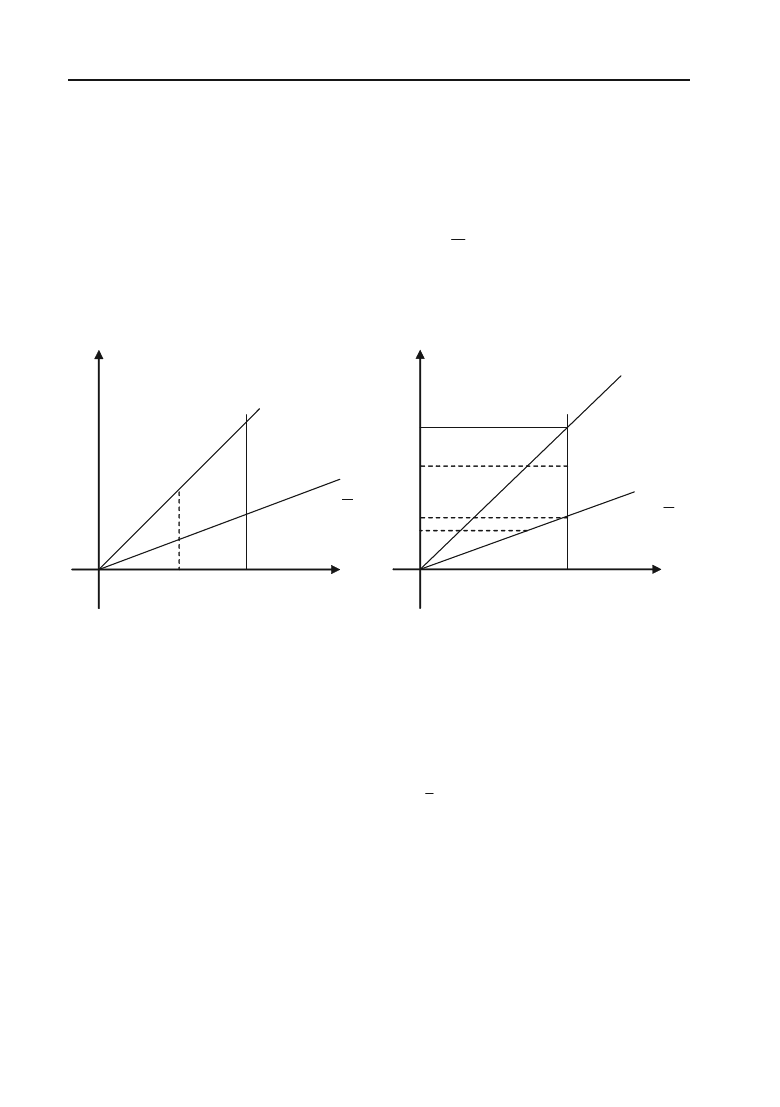
2. Якщо область інтегрування
V
обмежена кривою, яку будь+яка
пряма, що паралельна осі
Ох, перетинає не більше ніж в двох точках
(рис. 6.16), то подвійний інтеграл області
V
обчислюється за фор+
мулою:
(,)
f
xydxdy
V
³³
=
2
1
()
()
(,)
y
d
cy
dy f x y dx
M
M
³³
. (6.47)
Інтеграл в правій частині
цієї формули називається
по
вторним
. В формулі (6.47)
інтеграл
2
1
()
()
(,)
y
y
f
xydx
M
M
³
нази+
вається
внутрішнім. Тут межі
інтегрування є функції змінної
у. При обчисленні внутрішнь+
ого інтегралу в підінтегральній
функції потрібно
у розглядати
як величину сталу, а
х —
змінну. В результаті першого
(внутрішнього) інтегрування одержуємо функцію аргументу
у. Після
того, як ця функція визначена
2
1
()
()
() (,)
y
y
Фy fxydx
M
M
³
, необхідно ви+
конати зовнішнє (друге) інтегрування
()
d
c
Фydy
³
.
В результаті цього другого інтегрування одержуємо уже не фун+
кцію, а число.
Доведено, що якщо підінтегральна функція неперервна в області
V
, то результат інтегрування не залежить від порядку інтегрування.
Y
d
y
c
0
M N
X
1
()xy
M
2
()xy
M
Рис. 6.16.
460
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
6.12.2. Приклади розв’язання задач
Задача 6.295. Обчислити подвійний інтеграл
33
()
x
ydxdy
V
³³
,
якщо область
V
обмежена лініями y =
1
2
x; y = x; x = 4. Цей же
інтеграл обчислити, змінивши порядок інтегрування.
Розв’язок. Зобразимо на рисунку область
V
.
Контур цієї області перетинається будь+якою прямою, яка пара+
лельна осі
Оу, в двох точках. Використаємо спочатку формулу (6.46).
33
()
x
ydxdy
V
³³
=
4
0
dx
³
33
1
2
()
x
x
x
ydy
³
.
Тут у повторному інтегралі внутрішнє інтегрування виконується
по змінній
у, а зовнішнє — по х. Межі інтегрування в повторному
інтегралі одержано так: область
V
проектуємо на вісь Ох. Одержали
відрізок [0; 4]. Тим самим були визначені нижня 0 межа і верхня
межа — 4 зміни змінної
х у зовнішньому інтегралі. Потім на відрізку
[0; 4] осі
Ох вибрана довільна точка х, через яку проведена пряма,
що паралельна осі
Оу, і на ній відрізок MN, який знаходиться в об+
ласті
V
. Область
V
обмежена знизу прямою y = x, а зверху — пря+
0 х 4 Х
Y
C
B
N
M
y =
1
2
x
y = x
0 4 Х
Y
C
B
y =
1
2
x
y = x
4
2
2
V
1
V
A
Рис. 6.17.
