Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

461
Розділ VI. Інтегральне числення
мою у = х. Змінна у змінюється в області
V
від її значень x на нижній
частині контуру
ОВС до її значень х на верхній частині контуру
(рівняння ліній, що обмежують область
V
, повинні бути розв’язані
відносно тієї змінної, по якій обчислюється внутрішній інтеграл).
Обчислення необхідно починати з внутрішнього інтеграла
33
1
2
()
x
x
xydy
³
, в якому величина х повинна розглядатися як стала.
33
1
2
()
x
x
xydy
³
= (x
3
y +
4
4
y
)
1
2
x
x
= x
3
(x –
1
2
x) +
1
4
x
4
(1 –
1
16
) =
47
64
x
4
.
Відмітимо, що одержали функцію змінної х, як це повинно було
бути. Обчислюємо тепер зовнішній інтеграл:
4
4
0
47
64
xdx
³
=
47
64
5
4
0
5
x
=
47
64
5
4
5
=
752
5
.
Отже,
33
()x y dxdy
V
³³
=
4
0
dx
³
33
1
2
()
x
x
xydy
³
=
752
5
.
Обчислимо знову той же подвійний інтеграл, змінивши порядок
інтегрування і внутрішнє інтегрування будемо виконувати по змінній
х, а зовнішнє — по змінній у.
Із малюнка видно, що ліва частина контуру області
V
— одна
лінія, а саме
у = х, а його права частина складається із двох ліній ОВ
і ВС, що визначена різними рівняннями (ОВ) y =
1
2
x; (ВС) х = 4. в
такому випадку область необхідно розбити на частини так, щоб
кожна із них праворуч обмежувалась тільки однією лінією, тобто,
лінією, що визначена одним аналітичним виразом. Такими частина+
ми будуть
1
V
— ОАВ і
2
V
— АВС. Область
V
являється сумою об+
ластей
1
V
і
2
V
. Інтеграл можна представити як суму інтегралів:
462
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
33
()
x
ydxdy
V
³³
=
1
33
()xydxdy
V
³³
+
2
33
()xydxdy
V
³³
.
Так як тепер внутрішні будуть обчислюватися по змінній
х, то
рівняння ліній, що обмежують кожну із цих областей
1
V
і
2
V
по+
винні бути розв’язані відносно цієї змінної. Розв’язавши рівняння
ліній, що обмежують області
1
V
і
2
V
відносно змінної х, одержує+
мо, що область
1
V
обмежена лініями: 1) х = у; 2) х = 2у; 3) у = 2.
Точка
В має координати (4; 2). Область обмежена лініями: 1) у = 2;
2)
х = у; 3) х = 4. Спроектувавши кожну із цих областей
1
V
і
2
V
на
вісь
Оу, одержимо межі зовнішніх інтегралів: в першому інтегралі —
0 і 2, а в другому інтегралі — 2 і 4. Вибравши на відрізку [0; 2] дов+
ільну точку
у і провівши через неї пряму, яка паралельна осі Ох,
бачимо, що в області
1
V
змінна х змінюється від її значень, рівних
у на лівій частині контуру (тобто на ОА) до її значень 2у на його
правій частині(тобто на
ОВ). Таким чином, при інтегруванні по об+
ласті
1
V
у внутрішньому інтегралі межами будуть у та 2у. Маємо:
1
33
1
()x y dxdy
V
³³
=
2
0
dy
³
2
33
()
y
y
xydx
³
.
При обчисленні внутрішнього інтеграла змінна
у повинна вважа+
тися величиною сталою (а межі інтегрування є функції змінної
у, тоб+
то знову таки тієї змінної, яка при інтегруванні залишається сталою).
Обчислення починаємо з внутрішнього інтеграла:
2
33
()
y
y
x
ydx
³
= (
4
4
x
+ у
3
х)
2
0
=
1
4
((2у)
4
– у
4
) + у
3
(2у – у) =
19
4
у
4
.
Необхідно замітити, що одержали функцію змінної у, тобто тієї
змінної, за якою обчислюється зовнішній інтеграл. Підставляємо
одержаний вираз під знак інтеграла:
2
4
1
0
19
4
y
dy
³
=
19
4
5
2
0
5
y
=
152
5
.
463
Розділ VI. Інтегральне числення
Межі зовнішнього інтеграла при інтегруванні по області
2
V
були
визначені вище: змінна
у в цій області змінюється на відрізку [2; 4],
тобто від 2 до 4. Щоб визначити, в яких межах в цій області змінюєть+
ся змінна
х візьмемо на відрізку [2; 4] довільну точку, проведемо через
неї пряму, яка паралельна осі
Ох, і бачимо, що на лівій частині АС
контуру області
2
V
х має значення, рівні у, а на ВС — правій його
частині
х = 4. Таким чином в області
2
V
межами інтегрування по х
будуть у і 4, а
2
33
2
()x y dxdy
V
³³
=
4
2
dy
³
4
33
()
y
xydx
³
.
Внутрішній інтеграл (в ньому
у – величина стала).
4
33
()
y
xydx
³
= (
4
4
x
+ у
3
х)
4
y
=
1
4
(4
4
– у
4
) + у
3
(4 – у) = 64 + 4у
3
–
5
4
у
4
.
Зверніть увагу! Одержана функція змінної у, тобто тієї змінної,
по котрій обчислюється зовнішній інтеграл. Підставляємо одержа+
ний вираз під знак зовнішнього інтеграла:
4
34
2
2
5
(
64 4
)
4
yy
d
y
³
= (64у + у
4
–
1
4
у
5
)
4
2
= 120.
Шуканий інтеграл дорівнює сумі інтегралів:
=
1
+
2
=
152
5
+ 120 =
752
5
.
Так як підінтегральна функція (х
3
+ у
3
) — неперервна, то резуль+
тати співпали: вони не залежать від порядку інтегрування.
Із цього прикладу видно, що вибір порядку інтегрування не бай+
дужий. Вибравши раціонально порядок інтегрування можна скоро+
тити обчислення.
Задача 6.296. Обчислити подвійний інтеграл
33
()
x
yd
V
V
³³
,
якщо область інтегрування
V
, є трикутник, який обмежений прями+
ми
у = 0; х = 2; у = х/2.
464
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
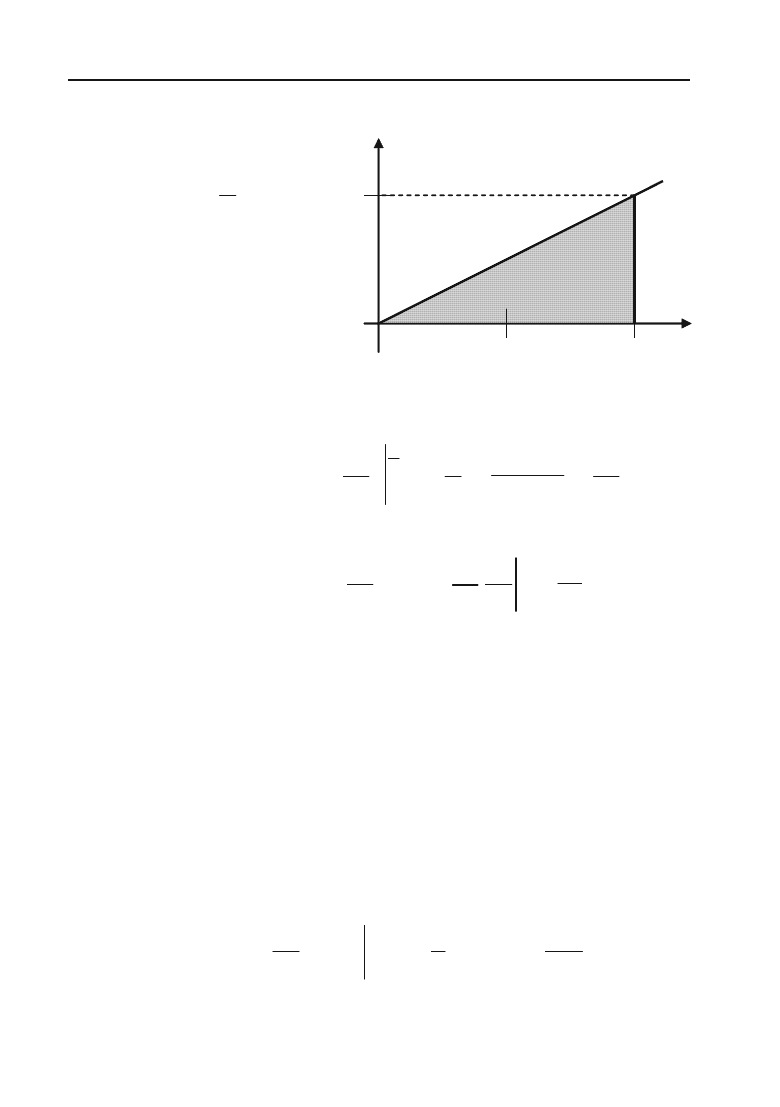
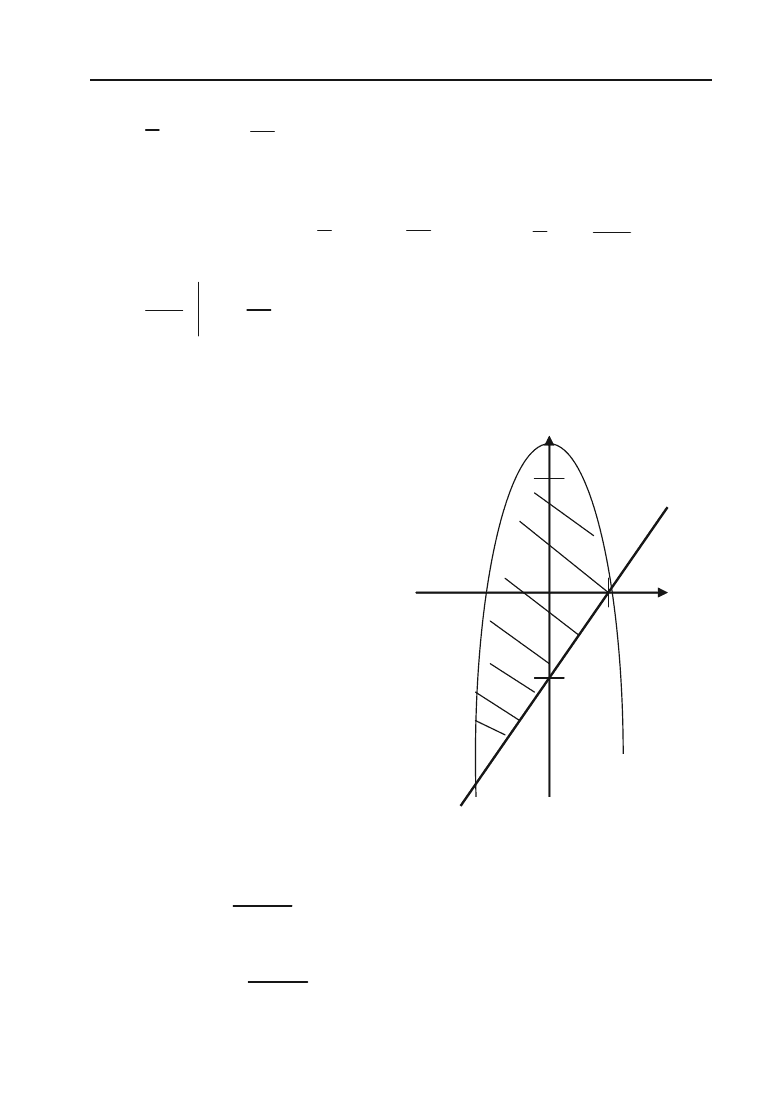
Розв’язок. Побудуємо область
V
.
02;
0.
2
x
x
y
dd
°
®
dd
°
¯
33
()
x
yd
V
V
³³
=
=
2
0
dx
³
/2
22
0
()
x
xydy
³
.
Обчислимо внутрішній
інтеграл, в якому
х вважаємо сталою.
/2
22
0
()
x
xydy
³
= (x
2
y +
3
3
y
)
2
0
x
= x
2
2
x
+
3
(/2)
3
x
=
13
24
x
3
.
Отже,
33
()
x
yd
V
V
³³
=
2
3
0
13
24
x
dx
³
=
13
24
4
2
0
4
x
=
13
6
.
Використаємо для обчислення подвійного інтегралу
33
()
x
yd
V
V
³³
формулу (6.47), межі інтегрування будуть:
01;
22.
y
yx
dd
®
dd
¯
33
()
x
yd
V
V
³³
=
1
0
dy
³
2
22
2
()
y
x
ydx
³
.
Так як
2
22
2
()
y
xydx
³
= (
3
3
x
+ у
2
х)
2
2
y
= (
8
3
+ 2у
2
) – (
3
8
3
y
+ 2у
3
) =
0 1 2 Х
Y
1
y = x/2
x = 2
Рис. 6.18.
465
Розділ VI. Інтегральне числення
=
8
3
+ 2у
2
–
14
3
у
3
,
то
33
()
x
yd
V
V
³³
=
1
23
0
814
2
33
yy
d
y
§·
¨¸
©¹
³
= (
8
3
у +
3
2
3
y
–
–
4
7
6
y
)
1
0
=
13
6
.
Задача 6.297. Знайти площу фігури, що обмежена лініями
у = 4 – х
2
, 3х – 2у – 6 = 0, за допомогою подвійного інтеграла.
Розв’язок. Якщо фігура, обме+
жена лініями, рівняння яких
віднесені до прямокутної системи
координат, то площа такої фігури
обчислюється за формулою
Sdxdy
V
³³
. Побудуємо цю фігу+
ру. Лінія
у = 4 – х
2
— парабола,
лінія 3
х – 2у – 6 = 0 є пряма (рис.
6.19).
Розв’язавши систему рівнянь
2
4,
3260,
yx
xy
®
¯
знайдемо координати точок пере+
тину параболи з прямою
2
4,
36
,
2
y
x
x
y
°
®
°
¯
36
2
x
= 4 – х
2
; 2x
2
+ 3x – 14 = 0;
Y
4
y
= x
/
2
y = (3x–6)/2
0 B X
C
A
–3
Рис. 6.19.
y = 4 – x
2
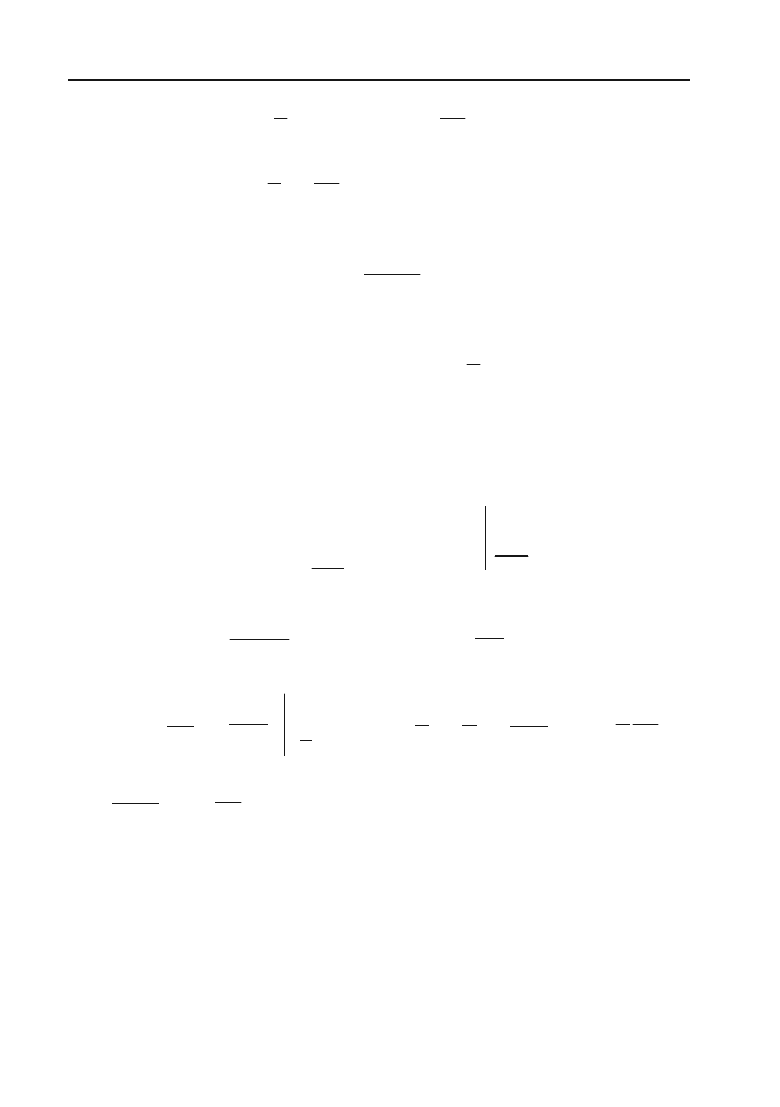
466
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
x
1
=
7
2
; x
2
= 2; y
1
=
33
4
; y
2
= 0.
Маємо точки
А(
7
2
;
33
4
) і В(2; 0).
Необхідно обчислити площу фігури
АВС. В області АВС змінна
у змінюється від значень
у =
36
2
x
на прямій АВ до значення
у = 4 – х
2
на параболі АСВ. (Знайдено межі для внутрішнього інтег+
рування). Змінна
у змінюється від х
А
=
7
2
до х
В
= 2. (Знайдено
межі для зовнішнього інтегрування). Таким чином, за формулою
S =
ABC
dxdy
³³
одержуємо:
S =
ABC
dxdy
³³
=
2
7/2
dx
³
2
4
36
2
x
x
dy
³
=
2
7/2
dx
³
у
2
36
2
4
x
x
=
=
2
2
7/2
36
(4 )
2
x
xdx
³
=
2
2
7/2
3
(7 )
2
x
x
dx
³
=
= (7х –
3
3
x
–
2
3
4
x
)
2
7
2
= (7
2+ 7
7
2
–
8
3
–
343
24
– 3 +
349
44
) =
=
1331
48
= 27
35
48
(кв. од).
6.12.3. Задачі для самостійного розв’язку
Задача 6.298. Обчислити задані подвійні інтеграли, для яких за+
дана прямокутна область інтегрування
D в дужках.
а)
D
x
ydxdy
³³
; (0
d
x
d
1; 0
d
y
d
2);

467
Розділ VI. Інтегральне числення
б)
xy
D
edxdy
³³
; (0
d
x
d
1; 0
d
y
d
1);
в)
2
2
1
D
x
dxdy
y
³³
; (0
d
x
d
1; 0
d
y
d
1).
Задача 6.299. Обчислити подвійний інтеграл
2
2
y
dxdy
x
V
³³
, де об+
ласть
V
обмежена лініями у =
1
3
х; у =
x
; х = 1.
Задача 6.300. Обчислити подвійний інтеграл
()
x
ydxdy
V
³³
, де
область
V
обмежена лініями: х = 0; у =
3
2
х (х
t
0); у = 4 – (х – 1)
2
.
Цей же інтеграл обчислити, змінивши порядок інтегрування.
Задача 6.301. Обчислити подвійний інтеграл
2
()
x
ydxdy
V
³³
,
де область
s обмежена лініями: у =
1
2
х; у = 2х; ху = 2 (х > 0).
Задача 6.302. Подвійним інтегралом обчислити площі фігур, що
задані лініями:
а)
xy = 4; y = x; x = 4;
б)
y
2
= 4 + x; x + 3y = 0;
в)
y = ln x; x – y = 1; y = –1;
г)
y = x + 2; y
2
= x; –2
d
y
d
2;
д)
y = sin x; y = cos x; x = 0;
ж) 3
x
2
= 25y; 5y
2
= 9x.

468
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розділ VIІ. Диференційні рівняння
Рівняння виду:
(,)
dy
fxy
dx
(7.1)
називається
диференційним рівнянням 1,го порядку, яке розв’яза+
не відносно похідної, де
f(х, у) задана і неперервна функція в деякій
області площини
хОу.
Якщо в частковому випадку
1
(,) ()
f
xy f x
{
, то рівняння (7.1)
матиме вигляд:
1
()
dy
fx
dx
, (7.2)
звідки
1
()
y
fxdxC
³
, (7.3)
тобто знаходження розв’язку рівняння (7.2) зводиться до обчислен+
ня інтегралу (7.3).
Загальним розв’язком рівняння (7.1) називається функція
(
,
)
y
xC
M
, (7.4)
яка задовольняє рівняння (7.1) при довільному
С, тобто:
(, )
(,(, ))
dxC
fx xC
dx
M
M
.
При конкретному значенні С = С
0
розв’язок
0
(, )
y
xC
M
нази+
вається
частковим. Якщо загальний розв’язок записаний в неявному
вигляді
F(х, у, С) = 0, то його називають загальним інтегралом дифе
ренційного рівняння
(7.1), а при С = С
0
— частковим інтегралом. Іноді
шукають не загальний розв’язок рівняння (7.1), а розв’язок, який
задовольняє умову
0
0
|
xx
y
y
. (7.5)

469
Розділ VII. Диференційні рівняння
§ 7.1. Рівняння з відокремленими змінними
Рівняння з відокремленими змінними це рівняння вигляду:
()()
y
fxgy
c
. (7.7)
Якщо
() 0gyz
, то його можна записати у вигляді:
()
()
dy
fxdx
gy
, (7.8)
і тоді говорять, що ми змінні відокремили. В загальному випадку
рівняння (7.1) є частковим випадком рівняння
f
1
(x, y)dx + f
2
(x, y)dy = 0. (7.9)
Рівняння (7.9) називають
рівнянням записаним в диференціалах і
воно є більш зручним для розв’язання. Оскільки змінні
х і у входять
в (7.9) симетрично, тому одну довільну змінну приймаємо за неза+
лежну, а другу за функцію.
Геометрично умова (7.5) означає, що шукається розв’язок (7.1),
який би проходив через точку (
х
0
, у
0
).Ця задача називається задачею
Коші.
Може трапитись, що існує розв’язок рівняння (7.1), який не
належить сім’ї розв’язків (7.4), такий розв’язок називається особли+
вим. Якщо рівняння (7.1) помножити на
dх і проінтегрувати по х
обидві частини (7.1), то одержимо:
(,)
y
fxydx C
³
, (7.6)
і може здатися, що формулою (7.6) відразу дається загальний розв’я+
зок (7.1), але це не так, тому що інтеграл
у за формулою (7.6) не
можна шукати, оскільки ми не знаємо як у залежить від
х.
Тому природно спочатку вказати методику розв’язання частко+
вих випадків рівняння (7.1).
7.1.1. Розв’язання прикладів
Приклад 7.1. Розв’язати рівняння xdx + ydy = 0.
Розв’язок.
В цьому рівнянні змінні відокремлені. Інтегруючи
обидві частини рівняння, одержимо:

470
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
22
222
xyC
,
або
х
2
+ у
2
= С,
і загальним інтегралом даного рівняння буде сім’я кіл з центром в
початку координат.
Приклад 7.2. Розв’язати рівняння
dy y
dx x
.
Розв’язок. Очевидно, що
0
y
{
буде розв’язком цього рівняння.
Нехай
0
y
z
. Тоді приведене рівняння можна записати у вигляді
dy dx
y
x
.
Інтегруючи, одержимо:
ln
|y| = ln |x| + ln C, або у = Сх.
Ми знайшли загальний розв’язок рівняння. При С = 0 загальний
розв’язок запишеться у вигляді:
у = 0.
Отже, значення у = 0 не буде особливим розв’язком цього рівняння.
Приклад 7.3. Розв’язати рівняння
y
c
= (х – у)
2
+ 1.
Розв’язок.
Тут легко здогадатися, яку потрібно зробити заміну
змінних, щоб звести це рівняння до рівняння з відокремленими
змінними. Робимо заміну
х – у = z. Продиференціюємо цю рівність
по
х, вважаючи, що у і z – функції від х.
1
–
y
c
=
z
c
,
y
c
= 1 –
z
c
.
І задане рівняння запишеться у вигляді:
1
–
z
c
= z + 1,
z
c
= –z,
0
z
z
,
dz
dx
z
,
ln
|z| = –x + ln C,
