Киселёв Ю.Н. Оптимальное управление
Подождите немного. Документ загружается.

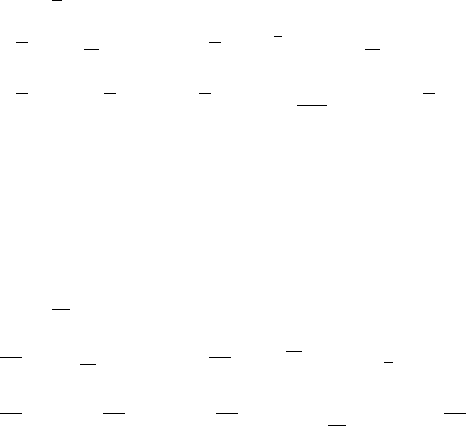
и множества управляемости
Z(t) ≡ Z(t, t
1
,M
1
)=e
(t−t
1
)A
M
1
+
t
1
t
e
(t−s)A
(−У) ds =
= e
(t−2π)A
M
1
+ S
2π−t
(0) = e
tA
M
1
+ S
2π−t
(0), 0 t 2π,
см. раздел 3.11.
При t =0имеем:
X(0) = S
π
(0) = M
0
,Z(0) = M
1
+ S
2π
(0),
X(0)
"
Z(0) = {x(0)} =
π
0
,ψ(0) =
1
0
(см. рисунок 13.19).
При t =
π
2
имеем:
X
π
2
= S
3π
2
(0),Z
π
2
= e
π
2
A
M
1
+ S
3π
2
(0),
X
π
2
"
Z
π
2
=
x
π
2
=
0
−3π
2
,ψ
π
2
=
0
−1
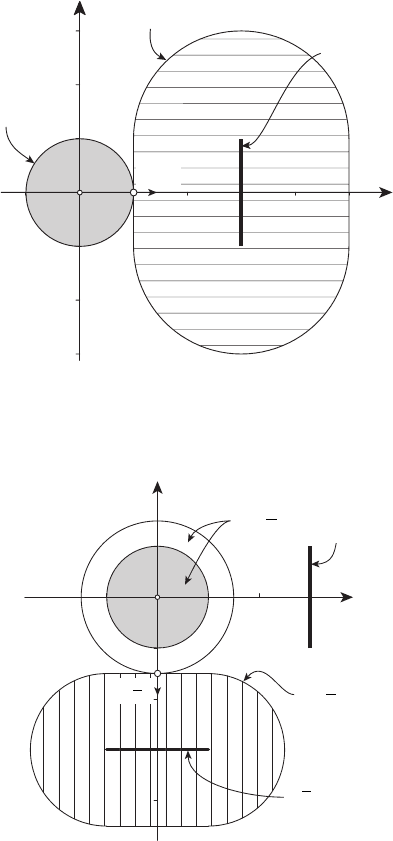
(см. рисунок 13.20).
При t = π имеем:
X(π)=S
2π
(0),Z(π)=e
πA
M
1
+ S
π
(0),e
πA
M
1
= −M
1
,
X(π)
"
Z(π)={x(π)} =
−2π
0
,ψ(π)=
−1
0
(см. рисунок 13.21).
При t =
3π
2
имеем:
X
3π
2
= S
5π
2
(0),Z
3π
2
= e
3π
2
A
M
1
+ S
π
2
(0),
X
3π
2
"
Z
3π
2
=
x
3π
2
=
0
5π
2
,ψ
3π
2
=
0
1
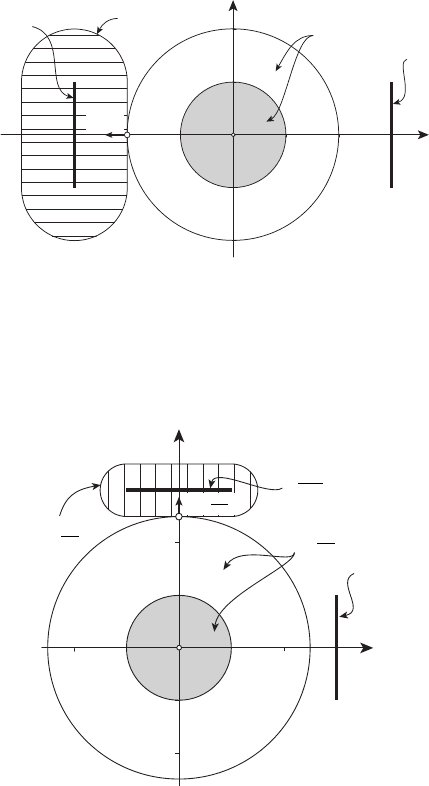
(см. рисунок 13.22).
Наконец, при t =2π имеем:
X(2π)=S
3π
(0),Z(2π)=M
1
,
X(2π)
"
Z(2π)={x(2π)} =
3π
0
,ψ(2π)=
1
0
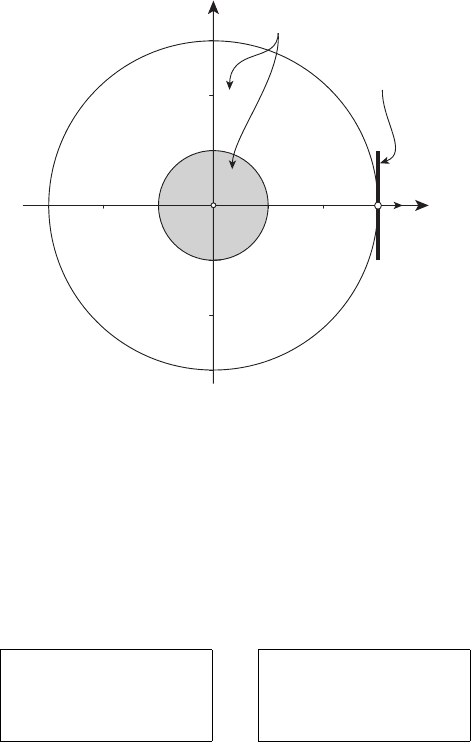
(см. рисунок 13.23).
141
x
1
x
2
0
π
2π
3π
−π
π
2π
3π
4π 5π
−π
−2π
−3π
M
0
M
1
X(0)
Z(0)
ψ(0)
Рисунок 13.19
x
1
x
2
0
−π
π
2π
3π
π
−π
−2π
−3π
−4π
M
0
M
1
X
π
2
Z
π
2
ψ
π
2
e
π
2
A
·M
1
Рисунок 13.20
142
x
1
x
2
0
−π
π
2π
−2π
π
2π
3π
−π
−2π
−3π−4π
M
0
M
1
X(π)
Z(π)
ψ(π)
e
πA
M
1
Рисунок 13.21
x
1
x
2
0
−π
π
2π
3π
−2π
π 2π 3π
−π
−2π
M
0
M
1
X
3π
2
Z
3π
2
ψ
3π
2
e
3πA
2
M
1
Рисунок 13.22
143
x
1
x
2
0
π 2π 3π
−π
2π3π
π
2π
3π
−π
−2π
−3π
M
0
M
1
= Z(2π)
ψ(2π)
X(2π)
Рисунок 13.23
3.14 Достаточные условия оптимальности в форме
принципа максимума с усиленными условиями
трансверсальности
В разделе 3.11 доказана теорема о необходимых условиях опти-
мальности в форме принципа максимума Понтрягина
M
0
, M
1
∈ conv Ω(E
n
)
пара (x(t),u(t))
оптимальна
=⇒
пара (x(t),u(t))
удовлетворяет
принципу максимума
Как показывают примеры (см. раздел 3.13, примеры 13.2, 13.4), об-
ратное утверждение неверно (т.е. пара (x(t),u(t)), удовлетворяю-
щая принципу максимума, может оказаться неоптимальной). Поэтому
важную роль играют теоремы о достаточных условиях оптимальности,
в которых содержится утверждение о том, что выполнение принци-
па максимума плюс некоторых дополнительных условий гарантирует
оптимальность рассматриваемой пары (x(t),u(t)), t
0
t t
1
.Роль
упомянутых дополнительных условий заключается в том, что они не
144
позволяют множеству достижимости X(t) ранее момента времени t
1
пересекаться с множеством конечных состояний M
1
.Теоремыодо-
статочных условиях оптимальности не предполагают выпуклости ком-
пактов M
0
, M
1
.
Теорема 14.1 (достаточных условиях оптимальности в фор-
ме принципа максимума с усиленными условиями трансверсаль-
ности).
Пусть
1) M
0
, M
1
∈ Ω(E
n
);
2) пара (x(t),u(t)) удовлетворяет принципу максимума Понтрягина
на отрезке [t
0
,t
1
] с сопряжённой переменной ψ(t);
3) с этой же сопряжённой переменной ψ(t) выполняется неравен-
ство
(x(t), −ψ(t)) >c(M
1
, −ψ(t)) ∀t ∈ [t
0
,t
1
) (1)
(усиленное условие трансверсальности на множестве M
1
).
Тогда пара (x(t),u(t)), t
0
t t
1
, оптимальна по быстродействию.
2 Условие (1) равносильно следующему
(x(t),ψ(t)) + c(M
1
, −ψ(t)) < 0 ∀t ∈ [t
0
,t
1
). (2)
Так как пара (x(t),u(t)) удовлетворяет принципу максимума, то, при-
влекая формулу (12) из раздела 3.11, условие (2) можно записать в
виде
c(X(t),ψ(t)) + c(M
1
, −ψ(t)) < 0 ∀t ∈ [t
0
,t
1
). (3)
Из условия (3) следует, что
X(t)
"
M
1
= ∅ ∀t ∈ [t
0
,t
1
) (4)
(применить первую часть свойства 14
0
опорных функций, раздел 2.5).
Условие (4) показывает, что объект неуправляем из M
0
в M
1
налюбом
отрезке [t
0
,t],гдеt<t
1
.Таккакx(t
1
) ∈ M
1
, x(t
1
) ∈ X(t
1
),то
x(t
1
) ∈ X(t
1
)
"
M
1
,т.е.
X(t
1
)
"
M
1
= ∅. (5)
Соотношения (4), (5) доказывают оптимальность пары (x(t),u(t)),
t
0
t t
1
.
145
Утверждение (4) вскрывает роль усиленного условия трансверсаль-
ности (1) в сочетании с принципом максимума. Принцип максимума
без дополнительного условия (1) не может гарантировать выполнение
геометрического условия (4) (см. пример 13.4, раздел 3.13).
Приведём примеры применения теоремы о достаточных услови-
ях оптимальности с усиленными условиями трансверсальности. Об-
ратимся к примеру 13.3 из раздела 3.13, в котором построена па-
ра (x(t),u(t)), 0 t t
1
, удовлетворяющая принципу максимума
с сопряжённой переменной ψ(t):
x(t)=(2π − t)
cos t
−sin t
,u(t)=ψ(t)=
−cos t
sin t
,t
1
= π.
Левая часть неравенства (1) в этом примере принимает вид
(x(t), −ψ(t)) = (2π − t)
cos
2
t +sin
2
t
=2π − t,
а его правая часть –
c(M
1
, −ψ(t)) = π−ψ(t)≡π,
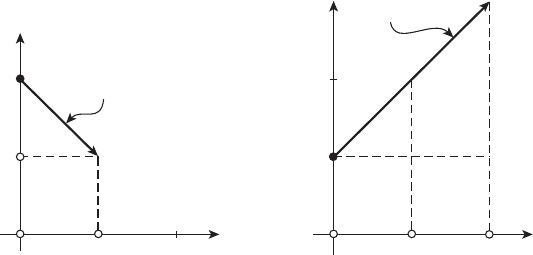
и, очевидно,
2π − t>π ∀t<t
1
= π,
(см. рисунок 14.1), т.е. выполнено усиленное условие трансверсаль-
ности (1); следовательно, пара (x(t),u(t)), 0 t π,оптимальна
(в разделе 3.13 вывод об оптимальности этой пары был сделан на
основании других соображений).
Замечание 14.1. Утверждение рассмотренной выше теоремы со-
храняется, если заменить условие (1) условием
(x(t),ψ(t)) >c(M
0
,ψ(t)) ∀t ∈ (t
0
,t
1
] (6)
(усиленное условие трансверсальности на множестве M
0
). Дей-
ствительно, условие (6) равносильно следующим:
c(M
0
,ψ(t)) + (x(t), − ψ(t)) < 0,
c(M
0
,ψ(t)) + c(Z(t), − ψ(t)) < 0,
M
0
"
Z(t)=∅,
∀t ∈ (t
0
,t
1
].
146
0
π
π
2π
2π
t
y
y =2π − t
0
π
π
2π
2π
t
y
y = π + t
Рисунок 14.1 Рисунок 14.2
Последние соотношения вместе с условием M
0
"
Z(t
0
) = ∅ приводят
к заключению об оптимальности пары (x(t),u(t)), t
0
t t
1
.
В некоторых примерах удобнее проверять условие (6) вместо усло-
вия (1). Обратимся к примеру 13.5 из раздела 3.13, в котором построе-
напара(x(t),u(t)), 0 t t
1
, удовлетворяющая принципу максимума
с сопряжённой переменной ψ(t):
x(t)=(π + t)
−cos t
sin t
,u(t)=ψ(t)=
−cos t
sin t
,t
1
= π.
Проверим выполнение усиленного условия трансверсальности в фор-
ме (6):
(x(t),ψ(t)) = π + t,
c(M
0
,ψ(t)) = π,
π + t>π ∀t ∈ (0,π],
(см. рисунок 14.2). Следовательно, построенная в этом примере па-
ра (x(t),u(t)), 0 t π, оптимальна.
Аналогичным образом проверяется условие (6) в примере 13.6 из
раздела 3.13, где t
0
=0, t
1
=2π,
x(t)=(π + t)
cos t
−sin t
,u(t)=ψ(t)=
cos t
−sin t
,
(x(t),ψ(t)) = π + t, c(M
0
,ψ(t)) = π,
π + t>π ∀t ∈ (0, 2π].
147
3.15 Локальная управляемость и её применения
В разделе 3.10 введено понятие управляемости объекта на задан-
ном отрезке времени [t
0
,t
1
] из множества M
0
в множество M
1
;управ-
ляемость равносильна условию
X(t
0
,t
1
,M
0
)
"
M
1
= ∅.
3.15.1 Локальная управляемость
Рассмотрим управляемый объект
˙x = Ax + u; У = У
U
; M
1
∈ Ω(E
n
);
пусть [t, t
1
] – заданный отрезок времени, t<t
1
.
Определение 15.1. Объект называется локально управляемым на
заданном отрезке времени [t, t
1
] на множестве M
1
, если существует
такое число ε>0, что для любой точки y ∈ M
1
+ S
ε
(0) объект явля-
ется управляемым на отрезке времени [t, t
1
] из одноточечного множе-
ства M
0
= {y} на множество M
1
. Другими словами, объект локально
управляем на отрезке времени [t, t
1
] на множестве M
1
,если
∃ε>0: M
1
+ S
ε
(0) ⊂ Z(t, t
1
,M
1
). (1)
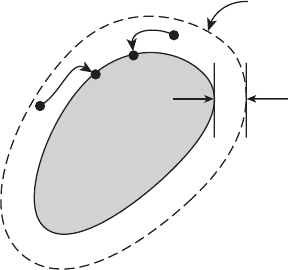
Это определение схематически иллюстрирует рисунок 15.1.
M
1
y
y
ε
M
1
+ S
ε
(0)
y, y
∈ M
1
+ S
ε
(0)
Рисунок 15.1
148
Из определения локальной управляемости в форме (1) вытекает
следующее необходимое условие локальной управляемости:
∃ε>0: c(M
1
,ψ)+εψ c(Z(t, t
1
,M
1
),ψ) ∀ψ ∈ E
n
. (2)
Из (2) следует, что
c(M
1
,ψ) <c(Z(t, t
1
,M
1
),ψ) ∀ψ ∈ S. (3)
В случае выпуклости компакта M
1
условия (2) и (3) являются не толь-
ко необходимыми, но и достаточными условиями локальной управляе-
мости (см. раздел 2.5, свойство 11
◦
опорных функций и следствие из
этого свойства).
3.15.2 Теорема о достаточных условиях оптимальности в форме
принципа максимума Понтрягина с условием локальной
управляемости
Теорема 15.1. Пусть
1) M
0
, M
1
∈ Ω(E
n
);
2) пара (x(t),u(t)) удовлетворяет принципу максимума Понтрягина
на отрезке [t
0
,t
1
];
3) объект локально управляем на множестве M
1
на любом отрезке
времени [t, t
1
], t
0
t<t
1
.
Тогда пара (x(t),u(t)), t
0
t t
1
, оптимальна.
2 Доказательство этой теоремы сводится к применению теоремы
раздела 3.14. По условию 3) данной теоремы (локальная управляе-
мость) для любого t ∈ [t
0
,t
1
)
∃ε>0: M
1
+ S
ε
(0) ⊂ Z(t) ≡ Z(t, t
1
,M
1
).
Отсюда на основании первой части свойства 11
0
и свойства 5
0
опор-
ных функций из раздела 2.5, следует, что
c(M
1
,ψ)+εψ c(Z(t),ψ) ∀ψ ∈ E
n
. (4)
Положим в (4) ψ = −ψ(t),гдеψ(t) – та сопряжённая переменная, с ко-
торой пара (x(t),u(t)) удовлетворяет принципу максимума (см. усло-
вие 2) данной теоремы); в результате этого последовательно получаем
c(M
1
, −ψ(t)) + ε−ψ(t) c(Z(t), −ψ(t)),
c(M
1
, −ψ(t)) <c(Z(t), −ψ(t)),t∈ [t
0
,t
1
). (5)
149
Привлекая лемму об эквивалентной формулировке принципа макси-
мума (раздел 3.11, подраздел 3.11.5), перепишем условие (5) в форме
c(M
1
, −ψ(t)) < (x(t), −ψ(t)),t∈ [t
0
,t
1
).
Последнее условие совпадает с усиленным условием трансверсально-
сти в форме (1), раздел 3.14. Теперь утверждение данной теоремы об
оптимальности пары (x(t),u(t)), t
0
t t
1
,вытекаетизтеоремы14.1
о достаточных условиях оптимальности с усиленным условием транс-
версальности на множестве M
1
.
Доказанная теорема часто оказывается более удобной для практи-
ческого применения при решении конкретных задач по сравнению с
теоремой 14.1.
3.15.3 Локальная управляемость в начало координат
Рассмотрим частный случай множества конечных состояний объ-
екта M
1
= {0}, состоящего из одной точки – начала координат про-
странства E
n
. Задача приведения объекта в начало координат часто
встречается в приложениях. Условие локальной управляемости в на-
чало координат на отрезке [t, t
1
] принимает следующий вид (см. (1)):
∃ε>0: S
ε
(0) ⊂ Z(t, t
1
, {0}). (6)
Условие (6) можно представить в форме
0 ∈ int Z(t, t
1
, {0}),
т.е. точка 0 ∈ E
n
является внутренней точкой множества управляе-
мости Z(t, t
1
, {0}) (см. рисунок 15.2).
В рассматриваемом случае M
1
= {0} множество управляемости
(см. раздел 1.3) допускает следующее представление
Z(t, t
1
, {0})=
t
1
t
e
(t−s)A
(−У) ds.
Поэтому вопрос о локальной управляемости в начало координат сво-
дится к вопросу о том, является ли точка 0 ∈ E
n
внутренней точ-
кой множества, определяемого интегралом. В следующем подразде-
ле 3.15.4 излагаются необходимые и достаточные условия для того,
150
