Киселёв Ю.Н. Оптимальное управление
Подождите немного. Документ загружается.

1.1.7 Линейная задача быстродействия
Линейная задача быстродействия является частным случаем зада-
чи оптимального управления (10) при условии (9) и в предположении
линейности функции f:
˙x = Ax + u, (12)
x(t
0
) ∈ M
0
,x(t
1
) ∈ M
1
, (13)
J = t
1
− t
0
→ min
u(·)∈У
U
. (14)
Здесь x =
⎛
⎜
⎝
x
1
.
.
.
x
n
⎞
⎟
⎠
– вектор фазовых координат; x ∈ E
n
,
A =(a
ij
) – матрица системы (считаем её независящей от време-
ни t),
u =
⎛
⎜
⎝
u
1
.
.
.
u
n
⎞
⎟
⎠
– вектор управления; u ∈ E
n
.
Класс допустимых управлений
У = У
U
=
u(t)
1) принимает значения из компакта U
2) задан характер зависимости u от t
.
Компакт U называется областью управления.
M
0
– множество начальных состояний объекта,
M
1
– множество конечных состояний объекта,
J = t
1
−t
0
– критерий качества управления (время перехода из M
0
в M
1
).
Линейная задача быстродействия (12)-(14) задаётся набором ис-
ходных данных
{A, M
0
,M
1
, У = У
U
,t
0
} (15)
и состоит в нахождении допустимого управления u = u(t),перево-
дящего объект из M
0
в M
1
по траекториям уравнения (12) за ми-
нимальное время. Управление u(t), решающее эту задачу, называется
оптимальным по быстродействию, а соответствующая этому управ-
лению траектория x(t) называется оптимальной по быстродействию
траекторией.
11
Решить задачу быстродействия (12)-(14) означает, что нужно по
набору исходных данных (15) найти оптимальную пару (x(t),u(t)),
t
0
t t
1
.
Векторное дифференциальное уравнение (12) равносильно системе
˙x
i
=
n
j=1
a
ij
x
j
+ u
i
,i=1,...,n.
1.1.8 Два простейших примера
Пример 1.1. Управляемое движение материальной точки по прямой
под действием ограниченной внешней силы (задача о тележке).
Рассмотрим материальную точку массы m, которая движется по
прямой (ось y) (см. рисунок 1.2), без трения под действием ограни-
ченной внешней силы, направленной вдоль оси y.
0
¯
f(t)
y
m
Рисунок 1.2
Геометрическое положение материальной точки описывается коор-
динатой y = y(t). На основании второго закона Ньютона запишем
дифференциальное уравнение движения точки
m¨y = f (t),
т.е.
¨y = v(t), (16)
где v(t)=
f(t)
m
– управление. Считаем заданными начальные усло-
вия y(0) = a (начальное положение точки), ˙y(0) = b (начальная ско-
рость точки). Дальнейшее движение точки зависит от выбора управ-
ления v(t), которое при m =1совпадает с f(t).Пустьуправлениеv(t)
подчинено ограничению
|v(t)| 1.
Рассмотрим задачу о переводе точки из начального положения a
при начальной скорости b в положение y =0с нулевой скоростью.
12
Этот перевод осуществляется за счёт выбора управления v(t).Требу-
ется выполнить этот перевод за кратчайшее время.
Полагая y = x
1
, ˙y = x
2
, v = u
2
,перейдёмотдифференциального
уравнения (16) второго порядка к следующей системе дифференци-
альных уравнений
˙x
1
= x
2
,
˙x
2
= u
2
.
В данном примере размерность фазового пространства равна 2, фа-
зовым пространством служит фазовая плоскость x
1
,x
2
. Множество
начальных состояний M
0
=
a
b
состоит из одной точки
a
b
,
множество конечных состояний M
1
=
0
0
– начало координат,
x =
x
1
x
2
–фазовыйвектор,A =
01
00
,областьуправления
U =
u =
u
1
u
2
u
1
=0
|u
2
| 1
– отрезок. Таким образом, мы получи-
ли линейную задачу быстродействия в стандартной форме (12)-(14).
Пример 1.2. Управляемое движение математического маятника
под действием ограниченной внешней силы.
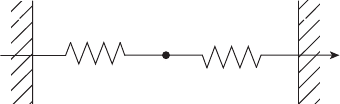
Рассмотрим движение тяжёлого шарика массы m под воздействием
упругой силы пружины и внешней силы f(t) (рисунок 1.3). Задача
рассматривается без учёта силы трения.
0
y
m
Рисунок 1.3
Движение шарика происходит вдоль оси y. В состоянии равнове-
сия шарик имеет координату y =0.Привлекаяфизическиезаконы–
второй закон Ньютона и закон Гука (упругая сила пропорциональна
отклонению от положения равновесия и направлена в сторону положе-
ния равновесия) – запишем дифференциальное уравнения движения
m¨y = −ky + f(t),
13
где положительный коэффициент k характеризует жёсткость пружи-
ны. Полагая ω
2
= k/m, v(t)=f(t)/m,приходимкуравнению
¨y + y = v(t) (17)
(здесь мы для упрощения считаем ω
2
=1, |v(t)| 1). Пусть заданы
начальные условия y(0) = a, ˙y(0) = b. Рассмотрим задачу о ско-
рейшем успокоении маятника под действием ограниченной внешней
силы v(t).
Полагая y = x
1
, ˙y = x
2
,v= u
2
, от уравнения (17) переходим к
системе
˙x
1
= x
2
,
˙x
2
= −x
1
+ u
2
.
Как и в предыдущем примере, здесь n =2,
M
0
=
a
b
,M
1
=
0
0
,
U =
u =
u
1
u
2
u
1
=0
|u
2
| 1
,x=
x
1
x
2
,
но теперь матрица системы имеет вид
A =
01
−10
.
Мы опять пришли к постановке линейной задачи быстродействия в
стандартной форме.
Решение этих примеров описывается в разделах 3.13, 3.16.
1.2 Некоторые сведения из теории обыкновенных
дифференциальных уравнений
При изучении линейной теории оптимального управления важную
роль играет формула Коши для решения линейной системы. В 1.2
приводится обоснование формулы Коши для линейных систем с по-
стоянными коэффициентами, изучается экспоненциал матрицы, рас-
смотрены примеры.
14
1.2.1 Формула Коши для решения начальной задачи в случае ли-
нейной системы обыкновенных дифференциальных урав-
нений
Скалярный случай (n =1). Рассмотрим задачу Коши
˙x = ax + u(t),x(t
0
)=x
0
, (1)
где x = x(t) – неизвестная скалярная функция аргумента t, u(t) –
известная непрерывная функция, a – заданное число, x
0
–заданное
начальное условие, t – независимая переменная (время), t
0
–началь-
ный момент времени.
Решение задачи Коши (1) определяется следующей формулой:
x(t)=e
(t−t
0
)a
⎛
⎝
x
0
+
t
t
0
e
−(s−t
0
)a
u(s) ds
⎞
⎠
. (2)
В этом можно убедиться непосредственной проверкой. Действи-
тельно, функция (2) удовлетворяет начальному условию x(t
0
)=x
0
и
является решением дифференциального уравнения, так как
˙x(t)=ae
(t−t
0
)a
⎛
⎝
x
0
+
t
t
0
e
−(s−t
0
)a
u(s) ds
⎞
⎠
+ e
−(t−t
0
)a
e
(t−t
0
)a
u(t)=
= ax(t)+u(t).
Формула (2) называется формулой Коши.
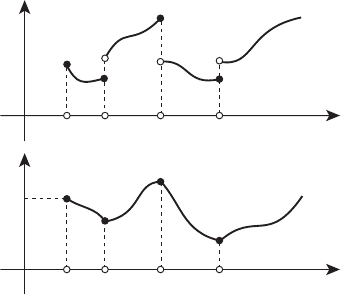
Замечание 2.1. Если u(t) – кусочно-непрерывная функция со скач-
ками в точках τ
1
,...,τ
s
, то формулой (2) определяется непрерыв-
ная кусочно-дифференцируемая функция x(t), которая удовлетворя-
ет дифференциальному уравнению ˙x(t)=ax(t)+u(t) ∀t = τ
1
,...,τ
s
;
производная ˙x(t) вточкахτ
1
,...,τ
s
имеет конечные скачки (см. ри-
сунок 2.1).
Общий случай (n>1). Рассмотрим задачу Коши
˙x = Ax + u(t),x(t
0
)=x
0
. (3)
Здесь
x =
⎛
⎜
⎝
x
1
.
.
.
x
n
⎞
⎟
⎠
,A=
⎛
⎝
a
11
... a
1n
... ... ...
a
n1
... a
nn
⎞
⎠
,u(t)=
⎛
⎜
⎝
u
1
(t)
.
.
.
u
n
(t)
⎞
⎟
⎠
,x
0
=
⎛
⎜
⎝
x
01
.
.
.
x
0n
⎞
⎟
⎠
;
15
0
0
t
t
x
u
t
0
t
0
τ
1
τ
1
τ
2
τ
2
τ
s
τ
s
x = x(t)
u = u(t)
Рисунок 2.1
x = x(t)– неизвестная векторная функция, u(t) – заданная непрерыв-
ная векторная функция, A – постоянная квадратная матрица, x
0
–
вектор начальных условий. Решение
x(t)=
⎛
⎜
⎝
x
1
(t)
.
.
.
x
n
(t)
⎞
⎟
⎠
задачи Коши (3) определяется формулой
x(t)=e
(t−t
0
)A
⎛
⎝
x
0
+
t
t
0
e
−(s−t
0
)A
u(s) ds
⎞
⎠
, (4)
или
x(t)=e
(t−t
0
)A
x
0
+
t
t
0
e
(t−s)A
u(s) ds. (5)
Формулы (4), (5) называются формулами Коши. В однородном
случае (u(t)=0)решение задачи Коши ˙x = Ax, x(t
0
)=x
0
,опреде-
ляется формулой
x(t)=e
(t−t
0
)A
x
0
. (6)
16
В формулах (4)-(6) участвует матричная функция e
(t−t
0
)A
,назы-
ваемая экспоненциалом матрицы A. В разделе 1.2.2 вводится поня-
тие экспоненциала, изучаются его основные свойства. После этого
нетрудно обосновать формулу Коши.
1.2.2 Экспоненциал постоянной квадратной матрицы. Его ос-
новные свойства. Обоснование формулы Коши
Рассмотрим квадратную матрицу n-ого порядка
D =
⎛
⎝
d
11
... d
1n
... ... ...
d
n1
... d
nn
⎞
⎠
D =
(D)
ij
n
i,j=1
, (D)
ij
= d
ij
,i,j=1,...,n.
Напомним известную из математического анализа формулу
e
t
=1+
t
1!
+
t
2
2!
+ ...+
t
k
k!
+ ... =
∞
k=0
t
k
k!
.
Этот степенной ряд сходится при всех t.
Определим теперь экспоненциал e
D
матрицы D,положив
e
D
= E +
1
1!
D +
1
2!
D
2
+ ...+
1
k!
D
k
+ ... =
∞
k=0
1
k!
D
k
. (7)
Здесь 0! = 1; D
O
= E – единичная матрица n-го порядка.
Таким образом, экспоненциал определён как сумма матричного ря-
да (7), члены которого являются квадратными матрицами порядка n.
Экспоненциал e
D
–квадратнаяматрицапорядкаn. Сходимость
матричного ряда (7) понимается в смысле поэлементной сходимости,
т.е.
(e
D
)
ij
=(E)
ij
+
1
1!
(D)
ij
+
1
2!
(D
2
)
ij
+ ...+
1
k!
(D
k
)
ij
+ .... (8)
ВслучаеD = tA,гдеt – скалярный множитель (в приложениях
t –время),A –(n × n)-матрица, получаем
e
tA
= E +
t
1!
A +
t
2
2!
A
2
+ ...+
t
k
k!
A
k
+ ... (9)
17

Теорема 2.1 (об основных свойствах экспоненциала).
1) Для любой (n×n)-матрицы D существует экспоненциал e
D
(схо-
дится матричный ряд (7), т.е. сходятся n
2
числовых рядов (8));
2) если A, B – две перестановочные (AB = BA) (n × n)-матрицы,
то
e
A
· e
B
= e
A+B
;
3) матрица e
D
невырождена, причём её обратная матрица опреде-
ляется равенством
e
D
−1
= e
(−D)
;
4) пусть D = tA; матричная функция e
tA
непрерывно дифференци-
руема, причём
d
dt
e
tA
= Ae
tA
= e
tA
A.
2 Доказательство.
1) Докажем сходимость числовых рядов (8) для любой матрицы D.
Для этого оценим общий член рядов (8). Пусть
|(D)
ij
| d, i, j =1,...,n.
Тогда
D
2
ij
=
n
α=1
(D)
iα
(D)
αj
nd
2
,
D
3
ij
n
2
d
3
,
...................................
индукция
D
k
ij
n
k−1
d
k
,
...................................
Отсюда получаем оценку общего члена ряда (8):
1
k!
(D
k
)
ij
1
n
(nd)
k
k!
. (10)
18
Теорема сравнения для числовых рядов, сходимость ряда
∞
k=1
1
n
(nd)
k
k!
=
e
nd
− 1
n
и неравенство (10) позволяют сделать заключение о сходимости
всех n
2
рядов (8), причём эти ряды сходятся абсолютно. Итак, эк-
поненциал e
D
определен для любой матрицы D.
2) Пусть AB = BA.Тогда
(A + B)
2
=(A + B)(A + B)=A
2
+ AB + BA + B
2
= A
2
+2AB+B
2
,
(A + B)
3
= A
3
+3A
2
B +3AB
2
+ B
3
,
.......................................................................
(A + B)
m
= A
m
+ mA
m−1
B + ...+ mAB
m−1
+ B
m
=
=
m
k=0
m!
k!(m − k)!
A
k
B
m−k
=
k+l=m
k, l0
m!
k! l!
A
k
B
l
, (11)
т.е. для перестановочных матриц A, B имеет место формула бинома
Ньютона,
m!
k!(m − k)!
– биномиальные коэффициенты. Привлекая (7),
(11), получаем:
e
A
· e
B
(7)
=
∞
k=0
1
k!
A
k
·
∞
l=0
1
l!
B
l
=
∞
k=0
∞
l=0
m!
k! l!
A
k
B
l
=
=
∞
m=0
1
m!
⎛
⎜
⎝
k+l=m
k, l0
m!
k! l!
A
k
B
l
⎞
⎟
⎠
=
∞
m=0
1
m!
(A + B)
m
(7)
= e
A+B
.
Задача 2.1. Привести примеры матриц A, B, для которых
e
A
· e
B
= e
A·B
.
3) Невырожденность экпоненциала и формула для его обращения
вытекают из части 2) рассматриваемой теоремы. Действительно, в
силу перестановочности матриц D и (−D) получаем:
e
D
· e
−D
= e
D−D
= e
O
= E, e
D
· e
−D
= E.
19
4) Докажем, что матричная функция e
tA
непрерывно дифферен-
цируема по аргументу t,т.е.каждыйеёэлемент(e
tA
)
ij
– непрерывно
дифференцируемая функция аргумента t.Таккак
e
tA
ij
=
∞
k=0
t
k
k!
(A
k
)
ij
(12)
– сумма степенного ряда относительно аргумента t (радиус сходимо-
сти этого ряда равен ∞), и степенные ряды можно дифференцировать
сколько угодно раз, причём при дифференцируемости радиус сходи-
мости не изменяется, то функции (12) аналитические. Следовательно,
существует производная
d
dt
(e
tA
),причём
d
dt
e
tA
=
d
dt
E + tA +
t
2
2!
A
2
+ ...+
t
k
k!
A
k
+ ...
=
= A + tA
2
+ ...+
t
k−1
(k − 1)!
A
k
+ ... =
= A
E + tA + ...+
t
k−1
(k − 1)!
A
k−1
+ ...
= Ae
tA
= e
tA
A.
Таким образом,
d
dt
e
tA
= Ae
tA
,e
tA
t=0
= E. (13)
Это свойство экcпоненциала позволяет проверить справедливость
формулы Коши при n>1 (подобно тому, как это было сделано выше
при n =1). Действительно, для векторной функции x(t), определяе-
мойформулой(4),выполняетсяначальноеусловиеx(t
0
)=x
0
и, кроме
того,
˙x(t)=Ae
(t−t
0
)A
⎛
⎝
x
0
+
t
t
0
e
−(s−t
0
)A
u(s) ds
⎞
⎠
+
+ e
(t−t
0
)A
e
−(t−t
0
)A
u(t)=Ax(t)+u(t),
т.е. функция (4) является решением задачи Коши (3).
Итак, доказана
20
