Киселёв Ю.Н. Оптимальное управление

Подождите немного. Документ загружается.

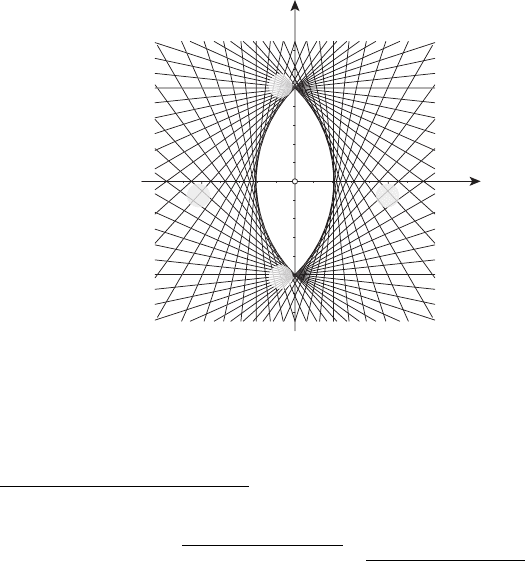
что выпуклый компакт F ⊂ E

может быть получен как пересече-

ние всех полупространств Π

,когдавекторψ пробегает единичную

сферу S:

F =

(

ψ∈S

, Π

= {x ∈ E

:(x, ψ)  c(F, ψ)}.

Так как каждое из опорных полупространств описывается с помощью

опорной функции c(F, ψ) компакта F ,тонаэтомпутимыприходим

к возможности аналитического описания выпуклых компактов при

помощи их опорных функций.

−1

Рисунок 5.1 б)

Эти геометрические соображения полезно иметь в виду при изу-

чении материала раздела 2.5.

и (−1, 0),выпуклымN-угольником. Можно показать, что опорная функция лунки

определяется формулой

c(L, ψ)=

)

+3ψ



− ψ



−

|ψ

+ ψ

| + |ψ

− ψ

При выполнении расчёта и создании рисунка 5.1 б) количество опорных прямых выбра-

но равным 60: наблюдается высокое качество приближения множества L пересечением

опорных полуплоскостей. В двух угловых точках лунки опорная прямая определяется

неединственным образом.

2.5.2 Определение опорной функции ограниченных множеств

Пусть F – ограниченное множество, лежащее в некотором ша-

ре S

(0) пространства E

, ψ – вектор пространства E

Определение 5.1. Опорной функцией множества F называется

функция, определяемая равенством

c(F, ψ)=sup

f∈F

(f,ψ). (1)

Опорная функция любого ограниченного множества принимает ко-

нечные значения при любом векторе ψ ∈ E

. Действительно,

|(f,ψ)|  f ψ,

(f,ψ)  ψ sup

f∈F

f, (2)

где число |F | =sup

f∈F

f,называемоемодулем множества F ,непре-

восходит R.Отсюдавытекаетоценка

c(F, ψ)  |F |ψ. (3)

Ясно также, что

|c(F, ψ)|  |F |ψ.

Замечание 5.1. Множество F может быть незамкнутым и невы-

пуклым.

Рассмотрим несколько примеров.

Пример 5.1. Рассмотрим на плоскости E

множество F = S

(0) –

круг радиуса 1 с центром в начале координат – и найдём его опорную

функцию:

c(F, ψ)= sup

f1

(f,ψ) = max

f1

(f,ψ)=ψ =

)

+ ψ

Пример 5.2. Рассмотрим на плоскости E

множество

F =

x ∈ E

: x

+ x

< 1

– открытый круг радиуса 1 с центром в начале координат – и найдём

его опорную функцию:

c(F, ψ)= sup

f<1

(f,ψ)=ψ =

)

+ ψ

Пример 5.3. Рассмотрим на плоскости E

множество

F = S ≡

x ∈ E

: x

+ x

– окружность радиуса 1 с центром в начале координат – и найдём её

опорную функцию:

c(F, ψ)= sup

f=1

(f,ψ) = max

f=1

(f,ψ)=ψ =

)

+ ψ

В рассмотренных выше трёх примерах различные множества име-

ют одну и ту же опорную функцию. Множества из примеров 5.1, 5.2

(замкнутый, открытый круги) связаны между собой: первое множе-

ство является замыканием второго. Имеется связь и между множе-

ствами из примеров 5.1 и 5.3: единичный круг S

(0) является наи-

меньшей выпуклой оболочкой окружности S.

Пример 5.4. Найдём опорную функцию множества

F =

x ∈ E

: |x

|  1, |x

|  1

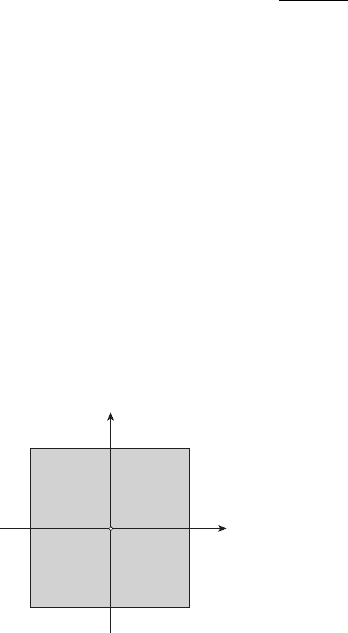
(квадрата, см. рисунок 5.2). Имеем

c(F, ψ) = max

f∈F

(f,ψ) = max

|1, |f

|1

+ f

)=|ψ

| + |ψ

−1

Рисунок 5.2

Упражнение 5.1. Выяснить, является ли опорная функция мно-

жеств из примеров 5.1–5.4 дифференцируемой функцией аргумента

ψ =(ψ

,ψ

Обсудим геометрический смысл опорной функции. Пусть F –ком-

пакт, c(F, ψ) – его опорная функция, а вектор ψ ∈ S,т.е.ψ =1,

c(F, ψ) = max

f∈F

(f,ψ)=(f

,ψ), f

∈ F (см. рисунок 5.3).

000

,ψ) < 0(f

,ψ)=0(f

,ψ) > 0

Рисунок 5.3

Опорная функция c(F,ψ)=(f

,ψ) равна наибольшей величине

проекций векторов f ∈ F на единичный вектор ψ.Знак(f

,ψ) харак-

теризует взаимное расположение множества F иточки0 относительно

опорной гиперплоскости Γ

:если(f

,ψ) > 0,токомпактF иначало

координат 0 расположеныпооднусторонуотопорнойгиперплоско-

сти Γ

, рисунок 5.3 а); если (f

,ψ)=0,то0 ∈ Γ

, рисунок 5.3 б);

если (f

,ψ) < 0,токомпактF иначалокоординат0 расположены по

разные стороны от опорной гиперплоскости Γ

, рисунок 5.3 в). При

ψ ∈ S опорная функция c(F, ψ) равна расстоянию от начала коорди-

нат до опорной гиперплоскости Γ

, причём расстоянию приписывается

определённый знак.

2.5.3 Cвойства опорных функций

Здесь будут рассмотрены 10 простейших свойств опорной функ-

ции.

Свойство1

◦

(опорная функция замыкания множества):

а) пусть F ∈ Ω(E

),тогда

c(F, ψ) = max

f∈F

(f,ψ);

б) пусть F – ограниченное множество, лежащее в пространстве E

F – замыкание множества F ,тогда

c(F, ψ)=c(

F,ψ).

2 В силу непрерывности скалярного произведения (f,ψ) (по аргу-

менту f ) для компактного множества F максимум скалярного про-

изведения (f,ψ) достигается в некоторой точке f

∈ F (теорема

Вейерштрасса), поэтому вместо точной верхней грани (sup)вформу-

ле (1) можно записать знак максимума (max), что доказывает утвер-

ждение а). Утверждение б) вытекает из определений опорной функ-

ции, замыкания множества и непрерывности скалярного произведе-

ния (f, ψ). 

Свойство 1

◦

можно проиллюстрировать примерами 5.1, 5.2.

Свойство 2

◦

(положительная однородность опорной функции

по второму аргументу):

c(F, λψ)=λc(F, ψ) ∀λ  0,ψ∈ E

2 Имеем:

c(F, λψ)=sup

f∈F

(f,λψ)=sup

f∈F

λ (f,ψ)=

= λ sup

f∈F

(f,ψ)=λc(F, ψ). 

Для множества F = S

(0) из примера 5.1 c(F,ψ)=

+ ψ

Пусть λ  0, ψ =(ψ

,ψ

),тогдаλψ =(λψ

,λψ

) и

c(F, λψ)=

(λψ

)

+(λψ

)

= λ

)

+ ψ

= λc(F, ψ) .

Проверить выполнение свойства 2

◦

для множества из примера 5.4.

Упражнение 5.2. Являютсялифункции

f(ψ

,ψ

)=ψ

+ ψ

,g(ψ

,ψ

)=1+

)

+ ψ

опорными функциями некоторого компакта F ∈ Ω(E

Свойство 3

◦

(полуаддитивность по второму аргументу):

c(F, ψ

+ ψ

)  c(F, ψ

)+c(F, ψ

) ∀ψ

,ψ

∈ E

2 Пусть

F – замыкание ограниченного множества F .Тогдамно-

жество

F ∈ Ω(E

).Привлекаясвойство1

◦

,получаем:

c(F, ψ

+ ψ

)=c(F,ψ

+ ψ

) = max

f∈F

(f,ψ

+ ψ

)=(f

,ψ

+ ψ

= {f

∈ F } =(f

,ψ

)+(f

,ψ

)  max

f∈F

(f,ψ

) + max

f∈F

(f,ψ

= c(

F,ψ

)+c(F,ψ

)=c(F, ψ

)+c(F, ψ

) . 

Упражнение 5.3. Доказать выпуклость опорной функции c(F, ψ)

по второму аргументу (использовать определение выпуклости функ-

ции и свойства 2

◦

, 3

◦

опорных функций). Проверить выполнение этого

утверждения в примере 5.1.

Свойство 4

◦

(условие Липшица по второму аргументу):

|c(F, ψ

) − c(F, ψ

)|  |F |·ψ

− ψ

∀ψ

,ψ

∈ E

;

здесь |F | =sup

f∈F

f – модуль множества F ; множитель |F | играет

роль константы Липшица.

2 Используя свойство 3

◦

,получаем:

c(F, ψ

)=c(F, (ψ

− ψ

)+ψ

)  c(F, ψ

− ψ

)+c(F, ψ

) .

Отсюда, привлекая неравенство (2), находим:

c(F, ψ

) − c(F, ψ

)  |F |·ψ

− ψ

.

Поменяв роли векторов ψ

и ψ

в предыдущих рассуждениях, прихо-

дим к неравенству

c(F, ψ

) − c(F, ψ

)  |F |·ψ

− ψ

.

Из двух последних неравенств вытекает двойное неравенство

−|F |·ψ

− ψ

  c(F, ψ

) − c(F, ψ

)  |F |·ψ

− ψ

,

т.е.

|c(F, ψ

) − c(F, ψ

)|  |F |·ψ

− ψ

. 

Следствие из свойства 4

◦

. Опорная функция c(F, ψ) непрерывна

по второму аргументу:

c(F, ψ



) → c(F, ψ),ψ



→ ψ.

Свойство 5

◦

(опорная функция линейно преобразованного мно-

жества):

пусть D – квадратная матрица n-го порядка, тогда

c(DF, ψ)=c(F, D

∗

ψ) ∀ψ ∈ E

где D

∗

– матрица, полученная из матрицы D транспонированием.

2 Свойство 5

◦

вытекает из определений опорной функции, опера-

ции линейного преобразования множества и свойств скалярного про-

изведения

c(DF, ψ)= sup

x∈DF

(x, ψ)= {x ∈ DF ⇔ x = Df, f ∈ F }

=sup

f∈F

(Df, ψ)=sup

f∈F

(f,D

∗

ψ)=c(F, D

∗

ψ) . 

В частном случае матрицы D = αE,гдеα –число,E – единичная

матрица, множество

DF =(αE)F = αF ,

и на основании свойства 5

◦

c(αF, ψ)=c(F, αψ) .

Если число α  0, то, привлекая свойство 2

◦

,получаем

c(αF, ψ)=α · c(F, ψ) ∀α  0,ψ∈ E

Итак, имеет место

Свойство 6

◦

(положительная однородность по первому аргу-

менту):

c(αF, ψ)=α · c(F, ψ) ∀α  0,ψ∈ E

Свойство 7

◦

(аддитивность по первому аргументу):

c(F

+ F

,ψ)=c(F

,ψ)+c(F

,ψ) .

2 Используя определения опорной функции и операции алгебраи-

ческого сложения множеств, получаем

c(F

+ F

,ψ)= sup

x∈F

(x, ψ)=

{x ∈ F

+ F

⇔ x = f

+ f

∈ F

}

=sup

∈F

+ f

,ψ)= sup

∈F

,ψ)+ sup

∈F

,ψ)=

= c(F

,ψ)+c(F

,ψ) . 

Свойство 8

◦

(опорная функция объединения множеств):

а) c(F

∪ F

,ψ) = max{c(F

,ψ),c(F

,ψ)},

б) для семейства {F

} равномерно ограниченных множеств, зави-

сящих от параметра λ, принадлежащего некоторому множеству Λ

(∃R>0: |F

|  R ∀λ ∈ Λ), имеет место формула



λ∈Λ

,ψ



=sup

λ∈Λ

c(F

,ψ) .

2 Вслучаеа)получаем

c(F

∪ F

,ψ)= sup

x∈F

∪F

(x, ψ) = max{sup

x∈F

(x, ψ), sup

x∈F

(x, ψ)} =

= max{c(F

,ψ),c(F

,ψ)}.

В случае б) множество

λ∈Λ

ограничено (оно принадлежит ша-

ру S

(0))и



λ∈Λ

,ψ



=sup

x∈

λ∈Λ

(x, ψ)=sup

λ∈Λ

sup

x∈F

(x, ψ)=sup

λ∈Λ

c(F

,ψ) . 

Свойство 9

◦

(опорная функция неотрицательной линейной ком-

бинации множеств):

пусть λ

, λ

– неотрицательные числа, F

, F

– ограниченные мно-

жества, лежащие в пространстве E

,тогда

c(λ

+ λ

,ψ)=λ

c(F

,ψ)+λ

c(F

,ψ) ∀ψ ∈ E

2 Свойство 9

◦

вытекает из свойств 7

◦

и 6

◦

. 

Свойство 10

◦

(совпадение опорных функций множества и его

наименьшей выпуклой оболочки):

c(F, ψ)=c(conv F, ψ) ∀ψ ∈ E

. (4)

2 В разделе 2.4 доказано, что conv F = H ≡

m0

,где

= F, F

m+1

λ∈[0,1]

{λF

+(1− λ)F

},m=0, 1,...

Привлекая свойство 8

◦

б), можно записать

c(conv F, ψ)=c

⎛

⎝

m0

,ψ

⎞

⎠

=sup

m0

c(F

,ψ) . (5)

Покажем, что

c(F

,ψ)=c(F, ψ),m=0, 1,... (6)

Тогда из (5), (6) вытекает утверждение (4) свойства 10

◦

. Ясно, что

c(F

,ψ)=c(F, ψ).ДалееF

λ∈[0,1]

{λF

+(1− λ)F

} и, используя

свойства 8

◦

б) и 9

◦

,получаем

c(F

,ψ)= sup

λ∈[0,1]

c(λF

+(1− λ)F

,ψ)=

=sup

λ∈[0,1]

{λc(F

,ψ)+(1− λ)c(F

,ψ)} =sup

λ∈[0,1]

c(F

,ψ)=c(F

,ψ) .

Итак, равенство (6) верно при m =0, 1; его справедливость для

любого номера m устанавливается индукцией. 

Мы изучили первую группу свойств (свойства 1

◦

– 10

◦

)опорных

функций. Далее рассмотрены примеры нахождения опорных функций

некоторых множеств. При разборе этих примеров привлекаются изу-

ченные выше свойства опорных функций.

2.5.4 Примеры

Пример 1. Найти опорную функцию множества

= S

(0) = {x ∈ E

: x  1}∈Ω(E

)

(единичного шара в пространстве E

). Так как

(f,ψ)  f ·ψ, (f, ψ)



ψ

= ψ,

то

c(F

,ψ) = max

f1

(f,ψ)=ψ =

)

+ ...+ ψ

Пример 2. Найти опорную функцию множества

= S

(0) ∈ Ω(E

)

(шара радиуса r  0 с центром в начале координат). Замечая, что

(0) = r · S

(0) и, используя свойство 6

◦

и результат примера 1,

получаем:

c(F

,ψ)=c(r · S

(0),ψ)=r · c(S

(0),ψ)=rψ.

Пример 3. Найти опорную функцию множества

= {a}∈Ω(E

состоящего из одной точки a ∈ E

. По определению опорной функции

c(F

,ψ)=(a, ψ)=a

+ ...+ a

Пример 4. Найти опорную функцию множества

= S

(a) ∈ Ω(E

)

(шара радиуса r  0 сцентромвточкеa ∈ E

). Привлекая равенство

(a)={a}+ S

(0), свойство 7

◦

и результат примеров 2, 3, получаем:

c(F

,ψ)=c({a},ψ)+c(S

(0),ψ)=

=(a, ψ)+r ψ = a

+ ...+ a

+ r

)

+ ...+ ψ

Установленное соотношение будет использовано при дальнейшем из-

ложении курса.

Пример 5. Найти опорную функцию множества

= {−v, v},v∈ E

состоящего из двух точек −v и v. Используя определение опорной

функции, получаем

c(F

,ψ) = max

(−v, ψ), (v, ψ)

= |(v, ψ)|.

Пример 6. Найти опорную функцию множества



−1







∈ Ω(E

состоящего из двух точек (−1, 0)

∗

и (1, 0)

∗

. По определению опорной

функции находим

c(F

,ψ) = max{−ψ

,ψ

} = |ψ

Пример 7. Найти опорную функцию множества

x ∈ E

: |x

|  1,x