Киселёв Ю.Н. Оптимальное управление
Подождите немного. Документ загружается.

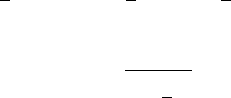
ки из начального состояния x
0
при помощи любого управления u
2
(t)
типа II, см. рисунок 13.2, фазовая точка никогда (при любом выборе
точки переключения τ) не попадет в начало координат, см. пунк-
тирную кривую II на рисунке 13.5. Если же, начиная движение из
начального состояния x
0
, использовать управление u
2
(t) типа I, см.
рисунок 13.2, то на начальном интервале u
2
(t)=−1, t ∈ (0,τ),идви-
жение фазовой точки будет происходить по параболе семейства (9),
проходящей через точку x
0
, см. кривую I на рисунке 13.5. Эта парабо-
ла I пересекается с линией AO вточкеy
0
. В момент τ,когдафазовая
точка попадает в точку y
0
, изменим знак управления u
2
(t),положив
u
2
(t)=+1. Тогда фазовая точка продолжит движение из точки y
0
по линии AO вверх и через некоторое конечное время попадает в на-
чало координат. При переключении управления u
2
(t) до попадания в
точку y
0
, либо после прохождения точки y
0
, управление типа I не
приводит к попаданию фазовой точки в начало координат.
В случае расположения начальной точки x
0
ниже линии AOB,
называемой линией переключения, задача попадания в начало ко-
ординат при помощи управлений u
2
(t), удовлетворяющих принципу
максимума, решается аналогичным образом при помощи управлений
типа II, см. рисунок 13.5.
Итак, для любой точки x
0
фазовой плоскости существует пара
(x(t),u(t)), удовлетворяющая принципу максимума Понтрягина, при-
чём эта пара единственна. Из сказанного в начале раздела 3.13 сле-
дует оптимальность построенной пары.
Найдем оптимальное время T (x
0
)=T (a, b) перехода из точки
x
0
=
a
b
в начало координат. Пусть точка x
0
лежит выше линии
переключения AOB.Тогда
T (a, b)=τ
x
0
y
0
+ τ
y
0
0
,
где τ
x
0
y
0
– время движения из точки x
0
вточкуy
0
,аτ
y
0
0
–время
движения из точки y
0
в начало координат.
Для нахождения координат точки y
0
рассматриваем систему урав-
нений
x
1
=
1
2
x
2
2
,x
1
= −
1
2
x
2
2
+ a +
1
2
b
2
,
инаходимординату(x
2
)
y
0
точки y
0
:
(x
2
)
y
0
= −
/
a +
1
2
b
2
.
121
Теперь находим
τ
x
0
y
0
=(x
2
)
x
0
− (x
2
)
y
0
= b +
/
a +
1
2
b
2
,
τ
y
0
0
=(x
2
)
0
− (x
2
)
y
0
=
/
a +
1
2
b
2
,
T (a, b)=b +2
/
a +
1
2
b
2
.
Если точка x
0
=
a
b
лежит ниже линии переключения AOB,то
(проверить!)
T (a, b)=−b +2
/
−a +
1
2
b
2
.
Окончательно,
T (a, b)=
⎧
⎨
⎩
b +2
)
a +
1
2
b
2
, если x
0
лежит выше линии AOB,
−b +2
)
−a +
1
2
b
2
, если x
0
лежит ниже линии AOB.
(10)
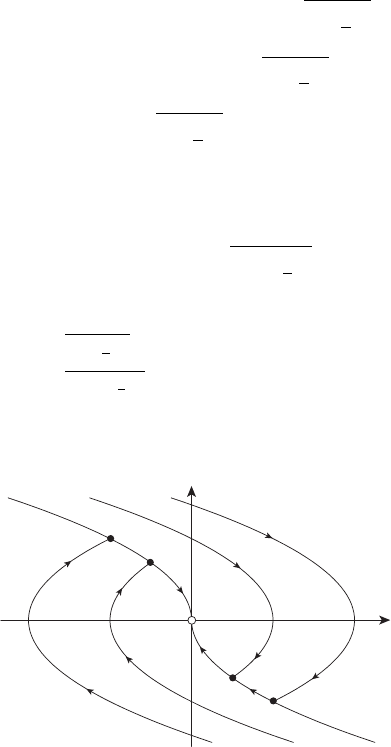
Вид оптимальных траекторий для различных начальных точек x
0
по-
казан на рисунке 13.6.
x
1
x
2
0
u
2
=+1
u
2
= −1
A
B
Рисунок 13.6
Выпишем формулы для оптимального управления u
2
(t) иопти-
мальной траектории (в случае точки x
0
=
a
b
, лежащей выше линии
122

AOB):
u
2
(t)=
−1, если 0 t<τ(a, b),
+1, если τ(a, b) <t T (a, b),
(11)
τ(a, b)=b +
/
a +
1
2
b
2
,T(a, b)=b +2
/
a +
1
2
b
2
,
x(t)=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
a + bt +
t
0
(t − s) u
2
(s) ds
b +
t
0
u
2
(s) ds
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠
, 0 t T (a, b).
Из рисунка 13.6 видим, что оптимальное управление
u
2
= v(x)=v(x
1
,x
2
)=
⎧
⎪
⎨
⎪
⎩
−1,
если точка x лежит выше
линии AOB или на BO,
+1,
если точка x лежит ниже
линии AOB или на AO.
(12)
Формулой (11) оптимальное управление определяется как функ-
ция времени t (или, как говорят, в программной форме, в форме про-
граммы). Формулой (12) оптимальное управление определяется как
функция фазовых координат объекта (или, как принято говорить, в
форме синтеза или в форме обратной связи). Знание управления в
форме синтеза важно для построения оптимальных регуляторов. При
подстановке управления (12) в уравнения движения объекта получаем
систему
˙x
1
= x
2
,
˙x
2
= v(x
1
,x
2
),
(13)
траектории которой изображены на рисунке 13.6. Система (13) нели-
нейна. Для реализации управляемого движения с использованием
синтезирующей функции v(x
1
,x
2
) к объекту необходимо присоеди-
нить измерительные устройства для нахождения текущих значений
фазового вектора x =(x
1
,x
2
).
В заключение рассмотрим изохроны рассматриваемого управля-
емого объекта, т.е. линии уровня функции оптимального времени
T (x
1
,x
2
), определяемой формулой (10). Семейство изохрон опреде-
ляется уравнением
T (x
1
,x
2
)=T, (14)
123

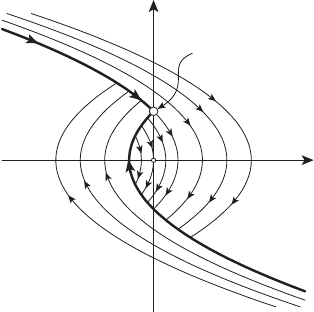
где T 0 – параметр. При T =0уравнению (14) удовлетворяет
единственная точка (0, 0).ПриT>0 вид изохрон изображён на ри-
сунке 13.7.
x
1
x
2
0
T (x
1
,x
2
)=T
A
B
R
P
Q
S
T
−T
Рисунок 13.7
Для всех точек x
0
, лежащих на линии PQRSP (рисунок 13.7),
определяемой уравнением (14), оптимальное время перехода из x
0
в
начало координат одинаково и равно T .ДугаPQR изохроны, лежа-
щая выше линии переключения AOB, является частью параболы
x
1
= −
(x
2
+ T )
2
4
+
T
2
2
, (15)
ветви которой направлены влево, а её вершина совпадает с точкой
P (
T
2
2
, −T ), лежащей на линии AO.ДугаRSP изохроны, лежащая
ниже линии переключения AOB, является частью параболы
x
1
=
(x
2
− T )
2
4
−
T
2
2
, (16)
ветви которой направлены вправо, а её вершина совпадает с точкой
R(
−T
2
2
,T), лежащей на линии BO. Параболы (15) и (16) пересекаются
вточкахP и R, причем пересечение происходит под ненулевым углом.
Изохрона PQRSP вточкахP и R имеет изломы.
Упражнение 13.2. Получить уравнения (15), (16), привлекая (10),
(14). Построить изохроны при T =
1
2
, 2, 4.
124
Упражнение 13.3. Доказать непрерывность функции T (x
1
,x
2
),
определяемой соотношением (10). Проверить, что функция T (x
1
,x
2
)
недифференцируема на линии переключения AOB.
Упражнение 13.4. Выяснить, какая существует связь между изо-
хронами и множествами управляемости.
Пример 13.2. Этот пример отличается от примера 13.1 только за-
данием множества M
1
=
0
1
. Вид оптимальных траекторий в приме-
ре 13.2 показан на рисунке 13.8, где AM
1
B – линия переключения.
Упражнение 13.5. Для примера 13.2 построить аналитическое
представление функции T (x
1
,x
2
), равной оптимальному времени пе-
рехода из начальной точки M
0
=
x
1
x
2
в конечную точку M
1
=
0
1
.
ЯвляетсялифункцияT (x
1
,x
2
) непрерывной? Построить изохроны.
x
1
x
2
0
u
2
=+1
u
2
= −1
A
B
M
1
Рисунок 13.8
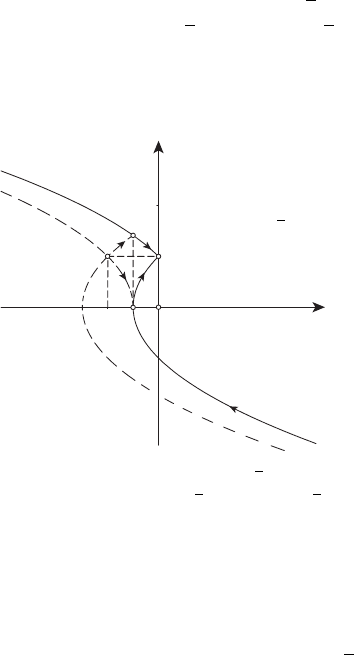
Рассмотрим более подробно задачу перехода из начальной точки
C
−1
1
в конечную точку M
1
0
1
за минимальное время (см. ри-
сунок 13.9). Точка C лежит на параболе семейства (9), проходящей
через точку E
−1/2
0
, в которой линия переключения пересекает
ось x
1
. Для начальной точки C существуют две траектории, удовле-
125
творяющие принципу максимума:
CDM
1
∼ u
2
(t)=
+1, 0 t
√
2 − 1,
−1,
√
2 − 1 <t 2(
√
2 − 1),
CEM
1
∼ u
2
(t)=
−1, 0 t 1,
+1, 1 <t 2.
x
1
x
2
0−1
2
A
B
C
D
E
M
1
C
−1
0
D
−1/2
√
2
E
−1/2
0
CDM
1
∼ u
2
(t)=
+1, 0 t<
√
2 − 1
−1,
√
2 − 1 <t 2(
√
2 − 1)
CEM
1
∼ u
2
(t)=
−1, 0 t<1
+1, 1 <t 2
Рисунок 13.9
Время перехода по траектории CDM
1
,равное2(
√
2 − 1) ≈ 0.82,
меньше времени перехода по траектории CEM
1
, равного 2. Опти-
мальной по быстродействию траекторией является траектория CDM
1
.
Рассмотренный пример показывает, что выполнения принципа мак-
симума, который, напомним, обоснован как необходимое условие оп-
тимальности (раздел 3.11), не всегда влечёт оптимальность. В разде-
лах 3.14, 3.15 проводится изучение достаточных условий оптималь-
ности. Ценность принципа максимума не снижается и в тех случа-
ях, когда пара (x(t),u(t)), удовлетворяющая принципу максимума,
неединственна. Принцип максимума позволяет выделить, вообще го-
воря, отдельные траектории, из которых дополнительным анализом
126
могут быть отобраны оптимальные. Так, в примере 13.2 с начальной
точкой C
−1
1
выделены траектории CDM
1
и CEM
1
,причёмпо-
следняя оказалась неоптимальной.
Упражнение 13.6. Указать начальные точки x
0
впримере13.2,
для которых неединственна пара (x(t),u(t)), удовлетворяющая прин-
ципу максимума.
Пример 13.3. Найти оптимальное управление и оптимальную тра-
екторию в линейной задаче быстродействия, в которой n =2, t
0
=0,
A =
01
−10
,U= S
1
(0),
M
0
= S
π
3π
0
,M
1
= S
π
(0),
т.е. в задаче
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
˙x
1
= x
2
+ u
1
,
˙x
2
= −x
1
+ u
2
,
x(0) ∈ M
0
,x(t
1
) ∈ M
1
,
u ∈ U = {u ∈ E
2
: u
2
1
+ u
2
2
1};
t
1
→ min .
(17)
Здесь u =
u
1
u
2
, x =
x
1
x
2
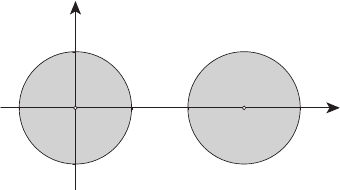
, область управления U является кру-
гом S
1
(0) радиуса 1 с центром в начале координат, множества M
0
,
M
1
являются кругами радиуса π (рисунок 13.10).
0
x
1
x
2
−π
−π
π
π
2π
3π
4π
M
0
M
1
Рисунок 13.10
Оптимальная пара
(x(t),u(t)), 0 t t
1
; x(t
0
) ∈ M
0
,x(t
1
) ∈ M
1
, (18)
127

удовлетворяет принципу максимума Понтрягина
а) (u(t),ψ(t)) = c(U, ψ(t)),t∈ [0,t
1
],
б) (x(t
0
),ψ(t
0
)) = c(M
0
,ψ(t
0
)),
в) (x(t
1
), −ψ(t
1
)) = c(M
1
, −ψ(t
1
)),
с некоторой сопряжённой переменной
ψ(t)=e
−tA
∗
ψ(0),ψ(0) ∈ S. (19)
Мы покажем, что пара (18), удовлетворяющая принципу максимума
а), б), в), существует и единственна. Кроме того, будет описана про-
цедура нахождения такой пары.
Выпишем опорные функции множеств U, M
0
, M
1
:
c(U, ψ)=ψ,c(M
0
,ψ)=3πψ
1
+ πψ,c(M
1
,ψ)=πψ. (20)
Привлекая первую из формул (20), запишем условие максимума а) в
форме
(u(t),ψ(t)) = ψ(t), u(t) 1,
откуда следует, что
u(t)=
ψ(t)
ψ(t)
. (21)
Так как
вслучаематрицыA =
01
−10
выполняется равенство
ψ(t) = ψ(0) и ψ(0) ∈ S,тоψ(t)≡1. Поэтому формулу (21)
можно записать в форме
u(t)=ψ(t), 0 t t
1
. (22)
Подчеркнём, что момент времени t
1
> 0 нам неизвестен; начальная
точка x(0) и конечная точка x(t
1
) траектории x(t) нам также пока
неизвестны; неизвестна пока и сопряжённая переменная ψ(t).
Из условия трансверсальности б) следует, что точка x(0) лежит
на границе круга M
0
и связана с вектором ψ(0) ∈ S соотношением
x(0) =
3π
0
+ πψ(0). (23)
128
0
x
1
x
2
π
2π
3π
4π
M
0
M
1
x(0)
x(t
1
)
ψ(0)
−ψ(t
1
)
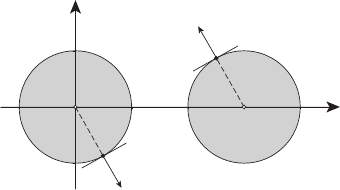
Рисунок 13.11
Из условия трансверсальности в) следует, что точка x(t
1
) лежит на
границе круга M
1
и связана с вектором ψ(t
1
) ∈ S соотношением
x(t
1
)=−πψ(t
1
). (24)
Геометрический смысл формул (23), (24) указан на рисунке 13.11.
Используя формулу Коши и соотношения (19), (22), (23), запишем
траекторию x(t) вформе
x(t)=e
tA
⎛
⎝
x(0) +
t
0
e
−sA
u(s) ds
⎞
⎠
=
%
формулы (19), (22), (23)
&
= e
tA
⎧
⎨
⎩
3π
0
+ πψ(0) +
t
0
e
−sA
e
−sA
∗
ψ(0) ds
⎫
⎬
⎭
=
%
e
−sA
e
−sA
∗
= E
&
= e
tA
3π
0
+(π + t)ψ(0)
,
таким образом,
x(t)=e
tA
3π
0
+(π + t) ψ(0)
, (25)
в частности,
x(t
1
)=e
t
1
A
3π
0
+(π + t
1
) ψ(0)
.
Привлекая последнюю формулу и формулу (19), запишем теперь усло-
129
вие(24)вформе:
e
t
1
A
3π
0
+(π + t
1
) ψ(0)
= −πe
−t
1
A
∗
ψ(0). (26)
Умножение равенства (26) на матрицу e
t
1
A
∗
иприведениеподобных
членов даёт
3π
0
= −(2π + t
1
) ψ(0). (27)
Принимая во внимание соотношения ψ(0) =1, t
1
> 0 исравнивая
модули векторов, стоящих в левой и правой частях равенства (27),
приходим к уравнению 3π = |2π + t
1
|,изкоторогонаходится
t
1
= π. (28)
Из (27), (28) получаем, что
ψ(0) =
−1
0
. (29)
Из формулы Коши (19) при t = t
1
с учётом (28), (29) находим
ψ(t
1
)=e
−t
1
A
∗
ψ(0) = e
−πA
∗
ψ(0) = −Eψ(0) =
1
0
. (30)
Теперь по формулам (23), (24) находим начальную и конечную точку
траектории x(t):
x(0) =
3π
0
+ π
−1
0
=
2π
0
, (31)
x(t
1
)=−π
1
0
=
−π
0
; (32)
по формуле (25) находим траекторию x(t):
x(t)=e
tA
3π
0
+(π + t)
−1
0
=
=(2π − t) e
tA
1
0
=(2π − t)
cos t
−sin t
, (33)
130
