Киселёв Ю.Н. Оптимальное управление
Подождите немного. Документ загружается.

достижимости и управляемости выражены в терминах исходных дан-
ных рассматриваемой линейной задачи быстродействия.
Свойство 3
◦
(о компактности и выпуклости множеств X(t),
Z(t)):
• если M
0
, M
1
∈ Ω(E
n
),тоX(t), Z(t) ∈ Ω(E
n
);
• если же M
0
, M
1
∈ conv Ω(E
n
),тоX(t), Z(t) ∈ conv Ω(E
n
).
2 Действительно, множества X(t) и Z(t), в соответствии с форму-
лами (1), (2), являются алгебраической суммой двух множеств. Вто-
рые слагаемые (интегралы) по теореме 6.2 являются выпуклыми ком-
пактами. Первые слагаемые, представляющие собой линейное преоб-
разование компактов M
0
, M
1
, являются компактами (проверить, что
умножение матрицы на компакт даёт компакт; умножение матрицы
на выпуклый компакт приводит к выпуклому компакту). Алгебраи-
ческая сумма двух компактов является компактом; алгебраическая
сумма двух выпуклых компактов является выпуклым компактом. Эти
соображения приводят к обоснованию свойства 3
◦
.
Замечание 8.1. Для одноточечных множеств M
0
, M
1
множест-
ва X(t), Z(t) являются выпуклыми компактами.
Свойство 4
◦
(непрерывная зависимость множеств X(t), Z(t) от
времени t):
h (X(t
),X(t)) → 0,h(Z(t
),Z(t)) → 0 при t
→ t.
Упражнение 8.1. Доказать свойство 4
◦
, привлекая формулы (1),
(2) и теорему 6.3 раздела 2.6.
3.9 Сопряжённое уравнение. Сопряжённая перемен-
ная. Лемма о сопряжённой переменной
Рассмотрим линейное дифференциальное уравнение
˙x = Ax + u(t),x∈ E
n
. (1)
Уравнение
˙
ψ = −A
∗
ψ (2)
называется сопряжённым уравнением для уравнения (1). Здесь
ψ =
⎛
⎜
⎝
ψ
1
.
.
.
ψ
n
⎞
⎟
⎠
91

– неизвестная n-мерная векторная функция аргумента t, A
∗
–матри-
ца, полученная транспонированием из матрицы A,входящейвуравне-
ние (1). Уравнение (2) является линейным однородным. Оно, очевидно,
имеет тривиальное решение ψ(t) ≡ 0. Это нулевое решение сопряжён-
ного уравнения нас не интересует в контексте изучения необходимых
условий оптимальности. Решение сопряжённого уравнения можно за-
писать с помощью формулы Коши:
ψ(t)=e
−(t−t
0
)A
∗
ψ(t
0
) (3)
(вектор начальных условий задан в момент времени t
0
).Всилуневы-
рожденности экспоненциала (раздел 1.2)
ψ(t) =0 ∀t ⇐⇒ ψ(t
0
) =0
т.е. тривиальное решение ψ(t) ≡ 0 уравнения (2) получаем только при
нулевом начальном условии ψ(t
0
)=0.
Определение 9.1. Любое нетривиальное решение ψ(t) сопряжён-
ного уравнения (2) будем называть сопряжённой переменной.
Для получения сопряжённой переменной ψ(t) следует решить со-
пряжённое уравнение (2) с некоторым ненулевым начальным услови-
ем.
Если начальное условие задано в момент времени t
1
, то вместо
формулы (3) получаем формулу
ψ(t)=e
−(t−t
1
)A
∗
ψ(t
1
). (4)
В дальнейшем изложении существенно используется следующая
лемма.
Лемма о сопряжённой переменной. Пусть t
0
<t
1
, t ∈ [t
0
,t
1
],
X(t) ≡ X(t
0
,t,M
0
) – множество достижимости, Z(t) ≡ Z(t, t
1
,M
1
) –
множество управляемости. Для любой сопряжённой переменной ψ(t)
имеют место следующие равенства
c(X(t),ψ(t)) = c(M
0
,ψ(t
0
)) +
t
t
0
c(U, ψ(s)) ds , (5)
c(Z(t), −ψ(t)) = c(M
1
, −ψ(t
1
)) +
t
1
t
c(U, ψ(s)) ds ; (6)
92
кроме того, справедливы соотношения
(x(t),ψ(t)) = (x(t
0
),ψ(t
0
)) +
t
t
0
(u(s),ψ(s)) ds , (7)
(x(t), −ψ(t)) = (x(t
1
), −ψ(t
1
)) +
t
1
t
(u(s),ψ(s)) ds , (8)
где ˙x(t)=Ax(t)+u(t) для почти всех t ∈ [t
0
,t
1
],т.е.вформу-
лах (7), (8) x(t) – любая траектория, отвечающая управлению u(t).
2 Равенства (5)-(8) устанавливаются непосредственной проверкой.
Проверим сначала равенство (7). На основании формулы Коши
x(t)=e
(t−t
0
)A
⎛
⎝
x(t
0
)+
t
t
0
e
−(s−t
0
)A
u(s) ds
⎞
⎠
,ψ(t)=e
−(t−t
0
)A
∗
ψ(t
0
).
Тогда скалярное произведение фазовой и сопряжённой переменных
допускает следующее преобразование:
(x(t),ψ(t)) =
⎛
⎝
e
(t−t
0
)A
x(t
0
)+
t
t
0
e
−(s−t
0
)A
u(s) ds
,e
−(t−t
0
)A
∗
ψ(t
0
)
⎞
⎠
=
=
⎛
⎝
x(t
0
)+
t
t
0
e
−(s−t
0
)A
u(s) ds, ψ(t
0
)
⎞
⎠
=
=(x(t
0
),ψ(t
0
)) +
t
t
0
(u(s),e
−(s−t
0
)A
∗
ψ(t
0
)) ds =
=(x(t
0
),ψ(t
0
)) +
t
t
0
(u(s),ψ(s)) ds.
Формула (7) доказана.
Проверимформулу(8).НаоснованииформулыКоши
x(t)=e
(t−t
1
)A
⎛
⎝
x(t
1
)+
t
t
1
e
−(s−t
1
)A
u(s) ds
⎞
⎠
,ψ(t)=e
−(t−t
1
)A
∗
ψ(t
1
).
93
Тогда
(x(t), −ψ(t)) =
=
⎛
⎝
e
(t−t
1
)A
⎛
⎝
x(t
1
)+
t
t
1
e
−(s−t
1
)A
u(s) ds
⎞
⎠
, −e
−(t−t
1
)A
∗
ψ(t
1
)
⎞
⎠
=
=(x(t
1
), −ψ(t
1
)) +
t
1
t
(u(s),e
−(s−t
1
)A
∗
ψ(t
1
)) ds =
=(x(t
1
), −ψ(t
1
)) +
t
1
t
(u(s),ψ(s)) ds.
Формула (8) доказана.
Проверим теперь формулу (5). Используя формулы (5) раздела 3.8,
и(3)раздела3.9,имеем
c(X(t),ψ(t)) = c(X(t),ψ)
ψ=ψ(t)
= c(M
0
,ψ(t
0
)) +
t
t
0
c(U, ψ(s) ds.
Для доказательства формулы (6) следует воспользоваться форму-
лами (6) раздела 3.8 и (4) раздела 3.9. Лемма о сопряжённой пере-
менной доказана.
Замечание 9.1. Опорная функция множества достижимости X(t)
на сопряжённой переменной ψ(t),т.е.функция
f(t) ≡ c(X(t),ψ(t)) = c(M
0
,ψ(t
0
)) +
t
t
0
c(U, ψ(s) ds,
непрерывна по аргументу t вместе со своей производной
˙
f(t)=c(U, ψ(t)).
Опорная функция множества управляемости Z(t) на сопряжённой пе-
ременной ψ(t),т.е.функция
ϕ(t) ≡ c(Z(t), −ψ(t)) = c(M
1
, −ψ(t
1
)) +
t
1
t
c(U, ψ(s) ds,
94

непрерывна по аргументу t вместе со своей производной
˙ϕ(t)=−c(U, ψ(t)).
3.10 Управляемость. Критерий управляемости. Ос-
новная лемма
В разделе 3.10 вводится понятие управляемости, рассматривается
критерий управляемости. С помощью критерия управляемости дока-
зывается так называемая основная лемма, которая будет использова-
на при выводе необходимых условий оптимальности в форме принципа
максимума Понтрягина (раздел 3.11).
Рассматривается управляемый объект, описываемый уравнением
˙x = Ax + u.
Задан класс допустимых управлений У = У
U
, множества M
0
, M
1
,
U, M
0
,M
1
∈ Ω(E
n
) идвачисла t
0
,t
1
; t
0
<t
1
.
Поставим вопрос: можно ли при помощи какого-нибудь допустимо-
го управления u(·) ∈ У, определённого на отрезке времени [t
0
,t
1
],
перевести объект из множества M
0
на множество M
1
:
x(t
0
) ∈ M
0
,x(t
1
) ∈ M
1
?
При положительном ответе на этот вопрос говорят об управляемо-
сти объекта. Исследование управляемости не связано с каким-либо
критерием качества процесса управления (например, со временем пе-
рехода). Отрезок времени [t
0
,t
1
] считается заданным.
Определение 10.1. Объект называется управляемым на задан-
ном отрезке времени [t
0
,t
1
] из множества M
0
вмножествоM
1
,
если существует допустимое управление u(·) ∈ У и отвечающая это-
му управлению траектория x(·) (т.е. ˙x(t)=Ax(t)+u(t) для почти всех
t ∈ [t
0
,t
1
]) сначальнымусловиемx(t
0
) ∈ M
0
такая, что x(t
1
) ∈ M
1
.
Из определения множества достижимости ясно, что объект управ-
ляем на заданном отрезке [t
0
,t
1
] из M
0
в M
1
тогда и только тогда,
когда множество достижимости X(t
1
) ≡ X(t
0
,t
1
,M
0
) пересекается с
множеством M
1
:
Управляемость на [t
0
,t
1
]
из M
0
в M
1
⇐⇒ X(t
0
,t
1
,M
0
)
"
M
1
= ∅ (1)
95
Так как X(t
1
), M
1
∈ Ω(E
n
), то, на основании утверждения (1) и пер-
вой части свойства 14
0
опорных функций (см. раздел 2.5), получаем
необходимое условие управляемости в форме
c(X(t
1
),ψ)+c(M
1
, −ψ) 0 ∀ψ ∈ E
n
,ψ=0, (2)
которое можно переписать, заменив ψ на ψ(t
1
),ввиде
c(X(t
1
),ψ(t
1
)) + c(M
1
, −ψ(t
1
)) 0 ∀ψ(t
1
) ∈ E
n
,ψ(t
1
) =0. (3)
Так как ψ(t
1
) =0, то этот ненулевой вектор в (3) можно рассмат-
ривать как значение сопряжённой переменной в момент времени t
1
.
Тогда, привлекая при t = t
1
формулу (5) раздела 3.9 из леммы о
сопряжённой переменной, условие (3) можно переписать в форме
c(M
0
,ψ(t
0
)) +
t
1
t
0
c(U, ψ(s)) ds + c(M
1
, −ψ(t
1
)) 0, (4)
причём условие (4) должно выполняться для любой сопряжённой пе-
ременной ψ(s):
ψ(s)
s=t
0
= ψ(t
0
),ψ(s)
s=t
1
= ψ(t
1
).
Итак, получено необходимое условие управляемости в форме (4) (пер-
вая часть следующей теоремы).
Теорема (критерий управляемости).
1) При M
0
, M
1
∈ Ω(E
n
) условие (4) является необходимым услови-
ем управляемости объекта на заданном отрезке времени [t
0
,t
1
]
из M
0
в M
1
.
2) При M
0
, M
1
∈ conv Ω(E
n
) условие (4) является необходимым
и достаточным условием управляемости объекта на заданном
отрезке времени [t
0
,t
1
] из M
0
в M
1
.
2 Часть 1) этой теоремы доказана выше. Для доказательства ча-
сти 2) остаётся проверить, что в случае выпуклых компактов M
0
,
M
1
условие (4) влечёт управляемость. Условие (4) равносильно усло-
вию (3), а условие (3) может быть записано в форме (2), т.е.
c(X(t
1
),ψ)+c(M
1
, −ψ) 0 ∀ψ ∈ E
n
.
96
Последнее условие и выпуклость компактов X(t
1
), M
1
наосновании
следствия из свойства 14
◦
раздела 2.5, влекут соотношение
X(t
1
)
"
M
1
= ∅,
равносильное управляемости, см. формулу (1). Критерий управляемо-
сти установлен.
Другая формулировка критерия управляемости. Перепишем
условие управляемости (4), заменив там сопряжённую переменную
по формуле (3) раздела 3.9:
c(M
0
,ψ(t
0
)) +
t
1
t
0
c(U, e
−(s−t
0
)A
∗
ψ(t
0
)) ds+
+ c(M
1
, −e
−(t
1
−t
0
)A
∗
ψ(t
0
)) 0 ∀ψ(t
0
) ∈ E
n
.
Введём функцию
Φ
0
(ψ)=c(M
0
,ψ)+
t
1
t
0
c(U, e
−(s−t
0
)A
∗
ψ) ds + c(M
1
, −e
−(t
1
−t
0
)A
∗
ψ) (5)
(функция управляемости). Положим
m
0
= min
ψ∈S
Φ
0
(ψ).
Ясно, что условие управляемости (4) равносильно каждому из следу-
ющих условий:
Φ
0
(ψ) 0 ∀ψ ∈ E
n
, (6)
Φ
0
(ψ) 0 ∀ψ ∈ S, (6
)
m
0
0. (6
)
Неравенства (6), (6
), (6
) являются другой формой условия управля-
емости (4) в терминах функции управляемости (5). Условия управля-
емости в форме (6
), (6
) удобны при рассмотрении конкретных при-
меров. Чтобы установить неуправляемость, достаточно указать такой
вектор
˜
ψ ∈ S,длякоторогоΦ
0
(
˜
ψ) < 0.
Упражнение 10.1. Записать условие управляемости в терминах
функции управляемости
Φ
1
(ψ)=c(M
0
,e
−(t
0
−t
1
)A
∗
ψ)+
t
1
t
0
c(U, e
−(s−t
1
)A
∗
ψ) ds+c(M
1
, −ψ). (7)
97
Какая связь существует между функциями управляемости (5) и (7)?
Пример 10.1. Пусть n =2, t
0
=0
A =
01
−10
,U= S
1
(0),
M
0
= S
π
3π
0
,M
1
= S
π
0
0
.
Исследовать управляемость объекта из M
0
в M
1
на отрезках времени
а) [0,π/2],б)[0,π],в)[0, 2π].
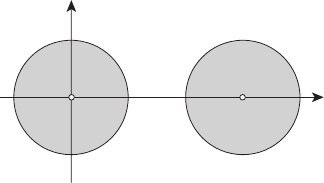
Множества M
0
, M
1
(см. рисунок 10.1) – выпуклые компакты, и
условие (6
) является необходимым и достаточным условием управ-
ляемости.
0
x
1
x
2
−π
−π
π
π 2π 3π
4π
M
0
M
1
Рисунок 10.1
Для решения вопроса об управляемости найдём функцию управляе-
мости Φ
0
(ψ) на отрезке [0,t
1
].Имеем:
c(M
0
,ψ)=3πψ
1
+ πψ,c(M
1
,ψ)=πψ,c(U, ψ)=ψ;
e
−(s−t
0
)A
∗
= e
−sA
∗
=
cos s sin s
−sin s cos s
,
c(U, e
−(s−t
0
)A
∗
ψ)=e
−sA
∗
ψ = ψ,
c(M
1
, −e
−(t
1
−t
0
)A
∗
ψ)=πe
−t
1
A
∗
ψ = πψ.
Находим теперь функцию управляемости (5)
Φ
0
(ψ)=
3πψ
1
+ πψ
+
t
1
0
ψ ds + πψ =3πψ
1
+(2π + t
1
) ψ
98

ичисло
m
0
= min
ψ=1
Φ
0
(ψ)=t
1
− π.
Условие управляемости (6
) принимает вид
t
1
− π 0.
Таким образом, на отрезке [0,t
1
] объект управляем при t
1
π и
неуправляем при 0 <t
1
<π. В частности, на отрезке [0,
π
2
] объект
неуправляем, а на отрезках [0,π], [0, 2π] объект управляем.
В примере 10.1 вопрос об управляемости был решён аналитиче-
скими средствами на основе критерия управляемости. Чтобы выяс-
нить геометрические причины управляемости или неуправляемости
на данном отрезке, мы в примере 10.2 изучим динамику множества
достижимости X(t)=X(0,t,M
0
) объекта из примера 10.1.
Пример 10.2. Найти множество достижимости X(t) для объекта
из примера 10.1 в произвольный момент времени t 0.
Привлекая формулу (5) раздела 3.8, (t
0
=0)
c(X(t),ψ)=c(M
0
,e
tA
∗
ψ)+
t
0
c(U, e
(t−s)A
∗
ψ) ds, (8)
найдём опорную функцию множества достижимости X(t).Имеем:
c(M
0
,ψ)=3πψ
1
+ πψ,
e
tA
∗
ψ =
cos t −sin t
sin t cos t
ψ
1
ψ
2
=
ψ
1
cos t − ψ
2
sin t
ψ
1
sin t + ψ
2
cos t
,
c(M
0
,e
tA
∗
ψ)=3π(ψ
1
cos t − ψ
2
sin t)+πe
tA
∗
ψ =
=(3π cos t)ψ
1
+(−3π sin t)ψ
2
+ πψ, (9)
t
0
c(U, e
(t−s)A
∗
ψ
) ds = t ψ. (10)
Тогда подстановка (9), (10) в (8) даёт
c(X(t),ψ)=(3π cos t)ψ
1
+(−3π sin t)ψ
2
+(π + t) ψ =
= c(S
r(t)
(a(t)),ψ), (11)
99
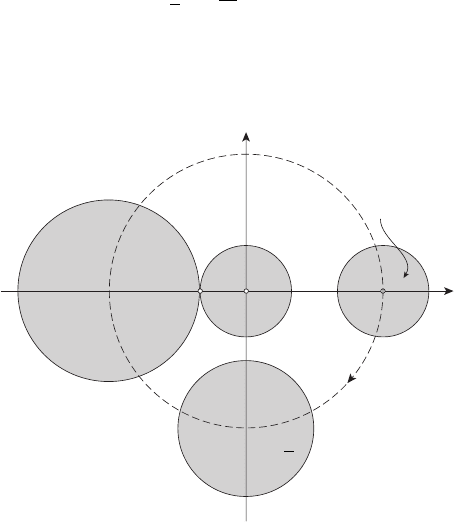
где r(t)=π + t, a(t)=3π
cos t
−sin t
. Из (11) следует, что
X(t)=S
r(t)
(a(t)),
т.е. множество достижимости X(t) является кругом радиуса r(t)=
π + t, центр которого a(t) движется по окружности радиуса 3π в
направлении вращения часовой стрелки (см. рисунок 10.2).
Ясно, что
X(t)
t=0
= S
π
3π
0
= M
0
,
X(t)
t=
π
2
= S
3π
2
0
−3π
,
X(t)
t=π
= S
2π
−3π
0
.
0
x
1
x
2
−π
−π
−3π
−3π
−5π
−5π
π
π 2π
3π
3π
4π
M
0
M
1
X(0) = M
0
X
π
2
X(π)
Рисунок 10.2
100
