Киселёв Ю.Н. Оптимальное управление

Подождите немного. Документ загружается.

x(t)

ψ(t)

−ψ(t)

X(t)

Z(t)

ψ(t)

Рисунок 11.4

3.12 Теорема существования оптимального управле-

ния

При доказательстве теоремы существования оптимального управ-

ления в линейной задаче быстродействия предполагается компакт-

ность множеств M

, M

(выпуклости этих множеств не требует-

ся) и существенно используется компактность множества достижи-

мости X(t) и его непрерывная зависимость от времени t (см. раз-

дел 3.8); кроме того, предполагается управляемость объекта из M

в M

на некотором конечном отрезке времени [t

,T].

В случае выпуклости компактов M

, M

доказательство теоремы

сильно упрощается (см. ниже замечание 12.1).

Теорема 12.1. Пусть

1) M

, M

∈ Ω(E

);

2) класс допустимых управлений У состоит из функций, интегри-

руемых по Лебегу;

3) на некотором конечном отрезке времени [t

,T] объект управляем

из M

в M

Тогда в классе допустимых управлений У существует оптимальное

управление u(t), t

 t  t

, t

 T , для рассматриваемой линейной

задачи быстродействия.

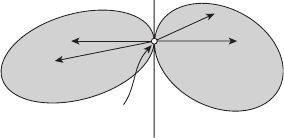
2 Пусть X(t)=X(t

,t,M

) – множество достижимости. По тре-

тьему условию теоремы

X(T )

= ∅, (1)

т.е. множество X(T ) имеет хотя бы одну общую точку с множе-

ством M

(см. рисунок 12.1).

111

X(T )

Рисунок 12.1

Рассмотрим множество

I = {t ∈ [t

,T]: X(t)

= ∅}.

Это множество непусто, так как T ∈ I,см.(1),иограниченоснизу

числом t

.Положим

=infI.

Из определения числа t

следует, что

X(t)

= ∅ при t

 t<t

. (2)

Мы покажем ниже, что

X(t

)

= ∅. (3)

Выполнение соотношений (2) и (3) означает оптимальность време-

ни t

. Из (3) и определения множества достижимости X(t

) следует

существование допустимого управления u(t), t

 t  t

,переводя-

щего объект из множества M

на множество M

. Это управление и

является оптимальным управлением для рассматриваемой линейной

задачи быстродействия.

Итак, остаётся доказать утверждение (3). Это доказательство опи-

рается на следующую лемму.

Лемма 12.1. Существует такая точка x

∗

∈ M

,что

∀ε>0 x

∗

∈ X(t

)+S

(0).

2 Возьмём последовательность {T

} такую, что

 t

→ t

при k →∞,X(T

)

= ∅ ∀k.

112

Возможность выбора такой последовательности {T

} вытекает из оп-

ределения числа t

. Существует такая точка x

∈ E

,что

∈ X(T

)

∀k. (4)

Так как x

∈ M

∀k,иM

– компакт, то из последовательности {x

}

можно выбрать сходящуюся к некоторой точке x

∗

∈ M

подпоследо-

вательность. Не изменяя обозначений, будем считать, что

→ x

∗

∈ M

,k→∞. (5)

Из непрерывной зависимости множества достижимости X(t) от вре-

мени t (свойство 4

◦

, раздел 3.8) и предельного соотношения T

→ t

(k →∞) следует, что

h(X(T

),X(t

)) → 0,k→∞. (6)

Из (5), (6) следует, что для любого числа ε>0

1) ∃k

= k

(ε) > 0: ∀k  k

x

∗

− x

 

т.е.

∀k  k

∗

∈{x

} + S

(0); (7)

2) ∃k

= k

(ε) > 0: ∀k  k

h(X(T

),X(t

)) 

и поэтому в силу определения расстояния Хаусдорфа

∀k  k

X(T

) ⊂ X(t

)+S

(0). (8)

Полагая k

= max{k

} и привлекая соотношения (7), (4), (8), по-

лучим (считая номер k  k

)

∗

(7)

∈{x

} + S

(0)

(4)

⊂ X(T

)+S

(0)

(8)

⊂ X(t

)+S

(0) + S

(0) =

= X(t

)+S

(0). (9)

Лемма 12.1 доказана. 

Покажем, в заключение, что утверждение (3) следует из доказан-

ной леммы 12.1. Действительно, положив ε =

, m =1, 2,...,имеем

∗

∈ M

и x

∗

∈ X(t

(0),m=1, 2,...

113

По определению алгебраической суммы двух множеств точку x

∗

мож-

но представить в виде

∗

= ξ

, где ξ

∈ X(t

), ψ

  1. (10)

В силу компактности множества достижимости X(t

) из последова-

тельности {ξ

} можно выбрать подпоследовательность, сходящуюся

к некоторой точке ξ

∗

∈ X(t

). Не изменяя обозначений, будем счи-

тать, что ξ

→ ξ

∗

, m →∞. Тогда предельный переход при m →∞

в (9) даёт x

∗

= ξ

∗

∈ X(t

), т.е. доказано соотношение (3), так как

∗

∈ X(t

) иодновременноx

∗

∈ M

. 

Замечание 12.1. В случае выпуклости компактов M

, M

тео-

рема существования оптимального управления доказывается намного

проще. Действительно, в силу выпуклости компактов X(T

) (свой-

ство 3

◦

,раздел3.8)иM

,условие

X(T

)

= ∅

на основании следствия из свойства 14

◦

раздела 2.5 равносильно усло-

вию

c(X(T

),ψ)+c(M

, −ψ)  0 ∀ψ ∈ S.

Перейдём в последнем неравенстве к пределу, устремив k к бесконеч-

ности (при каждом фиксированном ψ ∈ S). Тогда, используя свойство

непрерывности опорной функции по первому аргументу и условие (6),

получим неравенство

c(X(t

),ψ)+c(M

, −ψ)  0 ∀ψ ∈ S,

которое, в силу следствия из свойства 14

◦

раздела 2.5, равносильно

условию (3), что завершает доказательство теоремы существования в

случае M

, M

∈ conv Ω(E

3.13 Примеры применения необходимых условий оп-

тимальности для решения линейных задач быст-

родействия

Теорема о необходимых условиях оптимальности в форме прин-

ципа максимума Понтрягина (раздел 3.11) и теорема существования

оптимального управления (раздел 3.12) позволяют в рассмотренных

114

ниже примерах построить оптимальные решения. Здесь мы пользу-

емся следующей схемой рассуждений: если существует единственная

пара (x(t),u(t)), t

 t  t

, удовлетворяющая принципу максимума

Понтрягина, то эта пара является оптимальной. Действительно, нали-

чие такой пары обеспечивает управляемость объекта на отрезке [t

]

и (на основании теоремы из раздела 3.12) существование оптималь-

ного управления. Оптимальная пара должна удовлетворять принципу

максимума Понтрягина (теорема из раздела 3.11, подраздел 3.11.4), и

в силу единственности пары (x(t),u(t)), удовлетворяющей принципу

максимума, эта пара (x(t),u(t)) оптимальна.

В примерах 13.1, 13.2 множества M

, M

состоят из одной точки



при этом условия трансверсальности б), в) выполняются автомати-

чески и в анализе задачи участия не принимают



. В примере 13.1 па-

ра (x(t),u(t)), удовлетворяющая принципу максимума, единственна.

В примере 13.2 рассмотрена ситуация, когда пара (x(t),u(t)),удовле-

творяющая принципу максимума, неединственна; это обстоятельство

позволяет поставить вопрос об изучении достаточных условий оп-

тимальности (см. разделы 3.14, 3.15). Рассмотрены также примеры,

требующие привлечения условий трансверсальности.

Пример 13.1. Задача быстродействия для тележки. Рассмотрим

линейную задачу быстродействия при n =2, t

=0,

A =





,U=

u ∈ E

: u

=0, |u

|  1









т.е. следующую задачу

⎧

⎪

⎨

⎪

⎩

˙x

= x

(0) = a, x

(0) = b,

˙x

= u

)=0,x

)=0,

|  1,u∈ U = {u ∈ E

: u

=0, |u

|  1},

→ min .

(задача быстродействия для тележки, движущейся без трения под

действием ограниченной внешней силы). Множество M

начальных

состояний состоит из одной точки x





, а множество M

ко-

нечных состояний состоит из одной точки, совпадающей с началом

координат фазовой плоскости. Требуется перевести рассматриваемый

115

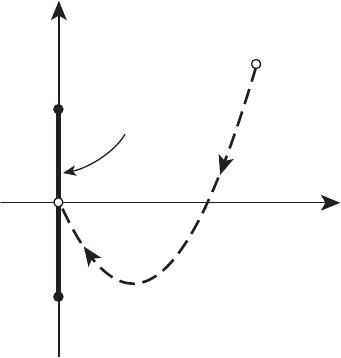
управляемый объект из точки x

в начало координат при помощи до-

пустимого управления за минимальное время. Область управления U

имеет форму отрезка (см. рисунок 13.1).

−1





Рисунок 13.1

Для решения этой задачи применяем принцип максимума Понтря-

гина



условие максимума а); условия трансверсальности б), в), кото-

рые для одноточечных множеств выполняются автоматически, в ре-

шении задачи участия не принимают



Пусть u(t)=



(t)



– оптимальное управление. Оно удовлетво-

ряет условию максимума

а) (u(t),ψ(t)) = c(U, ψ(t)) (1)

с некоторой сопряжённой переменной ψ(t)=



(t)



.Таккак

c(U, ψ)=|ψ

|,ψ=





то условие (1) принимает вид

(t) ψ

(t)+u

(t) ψ

(t)=|ψ

(t)|. (2)

116

Так как u(t) ∈ U,тоu

(t)=0,иусловие(2)можнозаписатьвформе

(t) ψ

(t)=|ψ

(t)|. (3)

Из (3) получаем, что

(t)= 1, если ψ

(t) > 0,

(t)=−1, если ψ

(t) < 0,

−1  u

(t)  1, если ψ

(t)=0.

(4)

Впоследнемслучае(ψ

(t)=0)управление u

(t) условием максиму-

ма (3) не определяется однозначно. Найдём сопряжённую переменную

ψ(t)=e

−tA

∗

ψ(0) =



−t 1







−tψ

+ ψ



;

здесь ψ(0) =





=0– вектор начальных значений сопряжённой

переменной. Таким образом,

(t) ≡ ψ

,ψ

(t)=−tψ

+ ψ

. (5)

Функция ψ

(t) линейно зависит от времени t и имеет не более одного

корня. Поэтому управление u

(t) однозначно определяется сопряжён-

ной переменной при всех t,крометогоt,длякоторогоψ

(t)=0,

см. (4). Итак,

(t)=sign ψ

(t). (6)

Принцип максимума, таким образом, позволил нам установить следу-

ющее очень важное качественное свойство оптимального управления



см. (6)



: оптимальное управление u

(t) является кусочно-постоянной

функцией времени t, принимающей значения ±1 и имеющей не более

одной точки переключения. В зависимости от начальных значений со-

пряжённой переменной ψ

, ψ

управление u

(t), определяемое фор-

мулой (6), может иметь только один из следующих типов (см. рису-

нок 13.2):

I. u

(t)=



−1, 0  t<τ

+1,τ<t

(одна точка переключения τ),

II. u

(t)=



+1, 0  t<τ

−1,τ<t

(одна точка переключения τ),

117

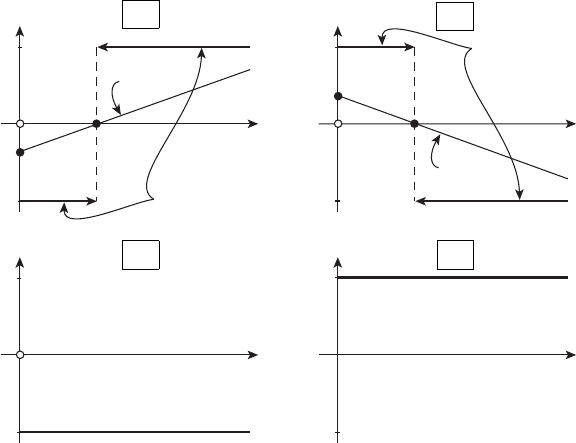
III. u

(t) ≡−1 (точек переключения нет),

IV. u

(t) ≡ +1 (точек переключения нет).

+1 +1

−1

−1 −1

−1

ττ

(t)

u = u

(t)

u = u

(t)

(t)=−1

(t)=+1

III IV

Рисунок 13.2

Упражнение 13.1. Выяснить, при каких условиях на ψ

, ψ

ре-

ализуется каждый из четырёх типов I–IV управления u

(t), t  0.

В точке переключения τ = ψ

/ψ

управление u

(t) условием

максимума не определяется однозначно, см. (4).

Таким образом, оптимальное управление u

(t) может иметь только

один из указанных четырех типов I–IV. Нам пока неизвестно, какой

именно тип оптимального управления u

(t) соответствует заданному

начальному состоянию объекта x

Чтобы решить последний вопрос, мы найдём сначала траектории

рассматриваемой управляемой системы при u

=+1,т.е.системы



˙x

= x

˙x

=+1.

(7)

118

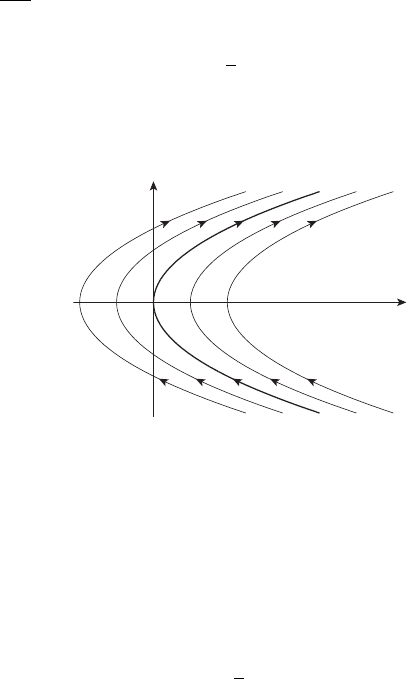
Имеем

= x

, откуда

+ c

, (8)

где c

– постоянная интегрирования. Уравнением (8) определяется

семейство парабол, изображённых на рисунке 13.3.

< 0 c

=0 c

> 0

Рисунок 13.3

Движение фазовой точки системы (7) по параболам семейства (8)

происходит снизу вверх при возрастании времени t, в силу того, что

˙x

=1> 0; направление движения фазовой точки с ростом времени t

отмечено на рисунке 13.3 стрелками.

При u

= −1 вместо семейства парабол (8) получаем семейство

парабол

= −

+ c

, (9)

изображённых на рисунке 13.4. Движение фазовой точки по парабо-

лам семейства (9) происходит сверху вниз, в силу того, что теперь

˙x

= −1 < 0.

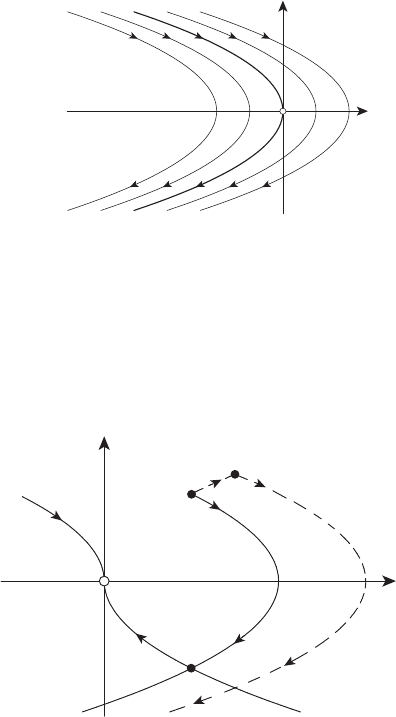
Поставим вопрос: из каких точек фазовой плоскости можно по-

пасть в начало координат за конечное время при помощи постоянного

управления u

(t) ≡ +1, т.е. по траекториям (8) системы (7)? Рассмот-

рение рисунка 13.3 позволяет получить следующий ответ: такие точки

расположены на части AO параболы семейства (8), проходящей через

начало координат (c

=0), см. рисунок 13.5.

119

< 0 c

=0 c

> 0

Рисунок 13.4

Те точки фазовой плоскости, из которых можно попасть в начало

координат за конечное время при помощи постоянного управления

(t) ≡−1, заполняют часть BO параболы семейства (9), проходящей

через начало координат (c

=0), см. рисунок 13.5.

=+1

= −1

Рисунок 13.5

Из точек фазовой плоскости, не лежащих на линии AOB,попасть

в начало координат при помощи постоянных управлений u

≡ +1 или

≡−1 невозможно (проверить!).

Рассмотрим теперь случай, когда точка x

(начальное состояние

объекта) расположена выше линии AOB. При движении фазовой точ-

120