Киселёв Ю.Н. Оптимальное управление
Подождите немного. Документ загружается.

и по формулам (22), (19) находим управление u(t):
u(t)=ψ(t)=e
−tA
∗
ψ(0) =
=
cos t sin t
−sin t cos t
−1
0
=
−cos t
sin t
. (34)
Таким образом, пара (18), удовлетворяющая принципу максимума,
единственна и определяется формулами (33), (34), (28). Следователь-
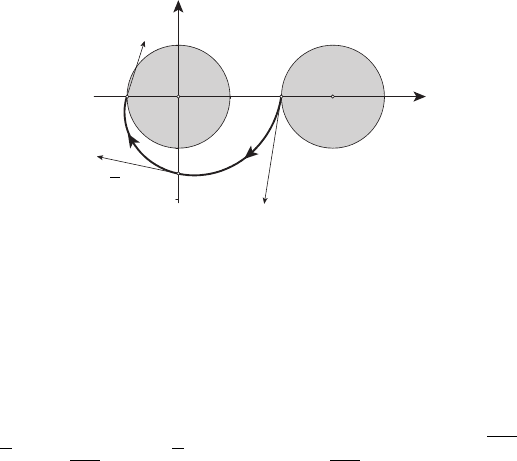
но, найденная пара (x(t),u(t)), 0 t π, оптимальна. Вид оптималь-
ной траектории показан на рисунке 13.12 жирной линией.
0
x
1
x
2
π
π
2π
3π
4π
−π
−π
M
0
M
1
˙x(0)
˙x
π
2
˙x(π)
Рисунок 13.12
При построении оптимальной траектории полезно учесть соотно-
шения:
x(0) =
2π
0
, ˙x(0) =
01
−10
2π
0
+
−1
0
=
−1
−2π
,
x
π
2
=
0
−3π
2
, ˙x
π
2
=
01
−10
0
−3π
2
+
0
1
=
−3π
2
1
,
x(π)=
−π
0
, ˙x(π)=
01
−10
−π
0
+
1
0
=
1
π
.
Итак, мы показали, решая пример 13.3, как может быть найдена
пара (18), удовлетворяющая принципу максимума. Приведём сейчас
другое решение этого же примера, опираясь на геометрические сооб-
ражения. Мы знаем, что для рассматриваемого управляемого объекта
множество достижимости X(t)=X(0,t,M
0
) является кругом (см.
131

раздел 3.10):
X(t)=S
r(t)
(a(t)),r(t)=π + t, a(t)=3π
cos t
−sin t
.
Круг X(t) при 0 t<t
1
= π не имеет общих точек с множе-
ством M
1
,априt = t
1
= π множество достижимости X(t) впервые
коснётся множества M
1
вточке
−π
0
:
X(π)
"
M
1
=
−π
0
.
Следовательно, t
1
= π – оптимальное время, x(t
1
)=
−π
0
– конеч-
ная точка оптимальной траектории; тогда, в силу условия трансвер-
сальности в),
ψ(t
1
)=−
1
π
x(t
1
)=
1
0
;
далее,
ψ(0) = e
−(0−t
1
)A
∗
ψ(t
1
)=e
πA
∗
ψ(t
1
)=−ψ(t
1
)=
−1
0
.
По найденному вектору ψ(0) из условия трансверсальности б) нахо-
дим x(0) =
2π
0
. Нахождение оптимальной пары (x(t),u(t)) произ-
водится, как указано выше, см. (33), (34).
В заключение обратимся к геометрической интерпретации сопря-
жённой переменной ψ(t), множества достижимости X(t)=X(0,t,M
0
)
и множества управляемости Z(t)=Z(t, π, M
1
):
X(t)=S
π+t
(a(t)),Z(t)=S
2π−t
(0),X(t)
"
Z(t)={x(t)}.
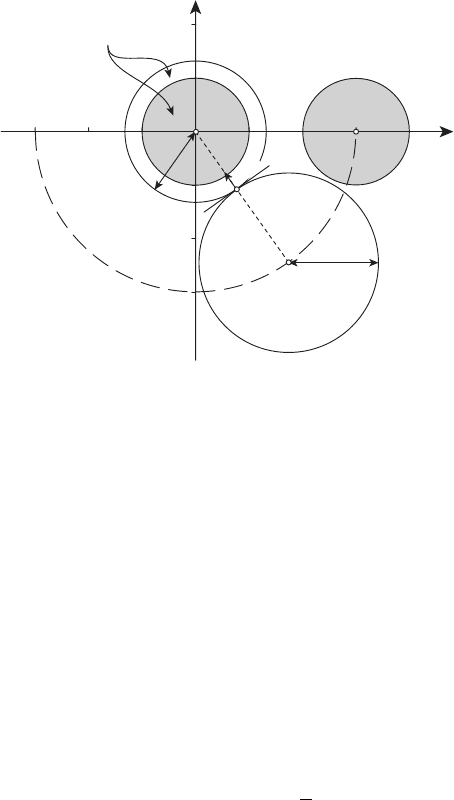
Расположение этих множеств и вектора ψ(t) указано на рисунке 13.13.
Пример 13.4 (неединственность экстремального процесса).
Рассмотрим линейную задачу быстродействия при n =2, t
0
=0,
A =
01
−10
,U= S
R
(0),M
0
= S
R
0
a
0
,M
1
=
0
−a
,
132
x
1
x
2
π
2π
3π 4π
−3π
M
0
M
1
X(t)
Z(t)
ψ(t)
a(t)
π+t
2π−t
Рисунок 13.13
где R = ρ/π, R
0
, a – положительные параметры,
2a
2
>R
2
0
. (35)
Условие (35) показывает, что круг M
0
несодержитточкиM
1
.
Здесь множество достижимости
X(t)=S
R
0
+tR
a cos t
−a sin t
,t 0,
является кругом, причём точка M
1
оказывается на границе множест-
ва X(t) в такие моменты времени t>0, которые являются корнями
уравнения
2a
2
(1 − sin t)=
R
0
+
t
π
ρ
2
. (36)
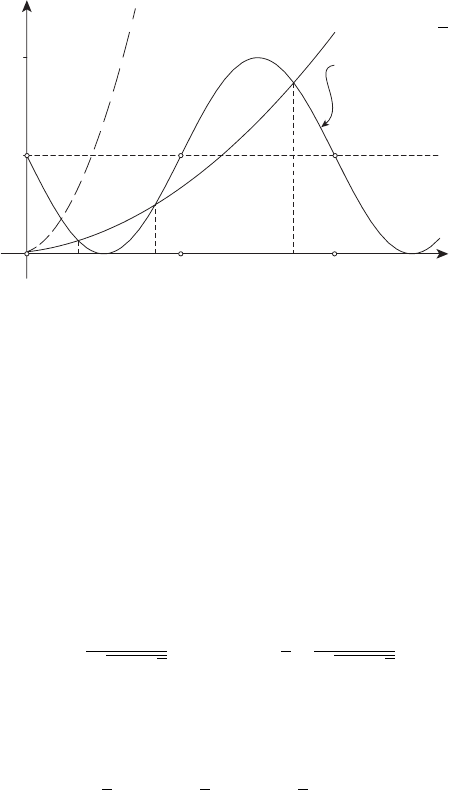
На рисунке 13.14 построены графики функций, стоящих в левой и
правой частях уравнения (36).
При условии (35) уравнение (36) всегда имеет хотя бы один поло-
жительный корень. При достаточно больших значениях параметра ρ
133
t
1
t
2
t
3
0
π
2π
t
y
R
2
0
2a
2
4a
2
y =
R
0
+
t
π
ρ
2
y =2a
2
(1 − sin t)
Рисунок 13.14
уравнение (36) имеет единственный положительный корень (см. пунк-
тирную кривую на рисунке 13.14). При уменьшении ρ у этого уравне-
ния появляются другие положительные корни. Пусть t
1
– наименьший
положительный корень уравнения (36). В момент времени t
1
множе-
ство достижимости X(t) впервые захватывает точку M
1
: t
1
–опти-
мальное время в примере 13.4. Оптимальное решение может быть
найденопосхеме,использованнойвпредыдущемпримере.
Рассмотрим ситуацию когда уравнение (36) имеет несколько поло-
жительных корней. Например, при
ρ =2
1 −
1
*
2+
√
3
a, R
0
=
1
3
5
*
2+
√
3
− 2
a (37)
корни уравнения (36) не зависят от a, и это уравнение имеет ровно
три положительных корня
t
1
=
1
3
π, t
2
=
5
6
π, t
3
≈
7
4
π − 0.05, (38)
причём
t
1
≈ 1.047197551,t
2
≈ 2.617993878,t
3
≈ 5.443787543.
Далее считаем a =1. В этом случае множество достижимости впер-
134
вые захватывает точку M
1
при t = t
1
:
X(t)
"
M
1
= ∅ при 0 t<t
1
,
X(t
1
)
"
M
1
= M
1
= ∅.
При t
1
<t<t
2
точка M
1
расположена внутри круга X(t). В момент
времени t
2
множество достижимости X(t) отрывается от точки M
1
:
X(t
2
)
"
M
1
= M
1
= ∅,
X(t)
"
M
1
= ∅ при t
2
<t<t
3
.
Наконец, в момент времени t
3
множество достижимости X(t) опять
накрывает точку M
1
,ивдальнейшемточкаM
1
лежит внутри X(t):
X(t
3
)
"
M
1
= M
1
= ∅,
X(t)
"
M
1
= M
1
= ∅ при t
3
<t.
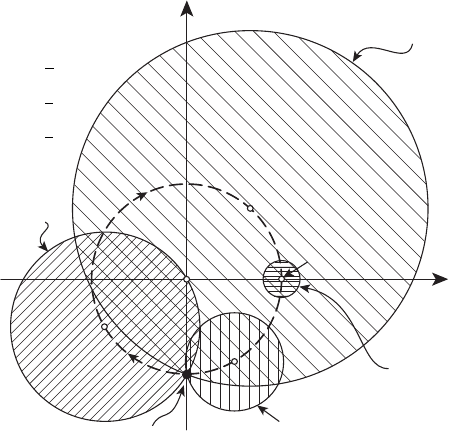
На рисунке 13.15 показаны множества достижимости X(t) при t = t
1
,
t
2
, t
3
.
Упражнение 13.7. В примере 13.4 построить оптимальную пару
(x(t),u(t)), 0 t t
1
.
Упражнение 13.8. Показать, что в случае (37), (38) на каждом
из отрезков [0,t
1
], [0,t
2
], [0,t
3
] может быть построена пара (x(t),u(t)),
удовлетворяющая принципу максимума. В каждом из этих случаев
построить траекторию x(t), соединяющую множество M
0
смноже-
ством M
1
.
Пример 13.5. Решить линейную задачу быстродействия, в которой
n =2, t
0
=0,
A =
01
−10
,U= S
1
(0),M
0
= S
π
(0),M
1
= S
π
3π
0
.
Этот пример отличается от примера 13.3 только выбором множеств
M
0
, M
1
.
Найдём пару (x(t),u(t)), 0 t t
1
, удовлетворяющую принципу
максимума с сопряжённой переменной ψ(t), ψ(0) ∈ S.Изусловия
максимума а) следует, что
u(t)=ψ(t), (39)
135
a =1
t
1
=
π
3
t
2
=
5
6
π
t
3
≈
7
4
π
0
x
1
x
2
M
0
M
1
a
X(t
1
)
X(t
2
)
X(t
3
)
Рисунок 13.15
а из условий трансверсальности б), в) получаем
x(0) = πψ(0), (40)
x(t
1
)=
3π
0
− πψ(t
1
). (41)
Привлекая формулу Коши и соотношения (39), (40), получаем
x(t)=e
tA
⎛
⎝
x(0) +
t
0
e
sA
u(s) ds
⎞
⎠
=(π + t) e
tA
ψ(0), (42)
в частности, при t = t
1
имеем:
x(t
1
)=(π + t
1
) e
t
1
A
ψ(0). (43)
136
Из (43), (41) получаем:
(π + t
1
) e
t
1
A
ψ(0) =
3π
0
− πe
−t
1
A
∗
ψ(0).
Отсюда с учётом равенства e
t
1
A
= e
−t
1
A
∗
следует, что
(2π + t
1
) e
t
1
A
ψ(0) =
3π
0
. (44)
Так как ψ(0) = e
t
1
A
ψ(0) =1, то из (44) вытекает, что 2π+t
1
=3π,
т.е.
t
1
= π. (45)
Из (44), (45) находим
ψ(0) = e
−πA
1
0
=
−10
0 −1
1
0
=
−1
0
. (46)
Из (40), (41), (46) получаем начальную и конечную точки траекто-
рии x(t):
x(0) = πψ(0) =
−π
0
,
x(t
1
)=
3π
0
− π
1
0
=
2π
0
.
Наконец, находим:
x(t)=(π + t) e
tA
ψ(0) = (π + t)
−cos t
sin t
,
u(t)=ψ(t)=e
−tA
∗
ψ(0) =
−cos t
sin t
,
⎫
⎪
⎪
⎬
⎪
⎪
⎭
0 t t
1
= π. (47)
Итак, найдена пара (x(t),u(t)), 0 t t
1
, см. (47), удовлетворя-
ющая принципу максимума. Эта пара единственна, и поэтому опти-
мальна. Оптимальная траектория x(t) изображена жирной линией на
рисунке 13.16.
137
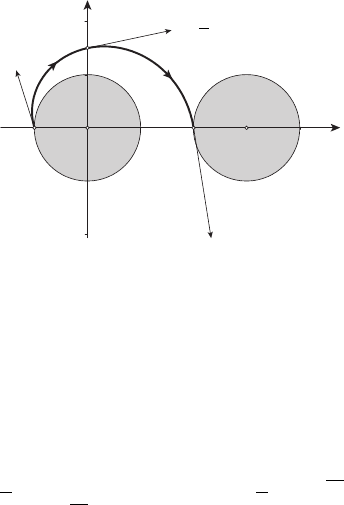
0
x
1
x
2
π
π
2π
3π
4π
−π
−π
M
0
M
1
˙x(0)
˙x
π
2
˙x(π)
Рисунок 13.16
При построении оптимальной траектории полезно учесть соотно-
шения
x(0) =
−π
0
, ˙x(0) =
−1
π
,
x
π
2
=
0
3π
2
, ˙x
π
2
=
3π
2
1
,
x(π)=
2π
0
, ˙x(π)=
1
−2π
.
Упражнение 13.9. Изучить динамику множества достижимос-
ти X(t) в примере 13.2 и на этой основе дать геометрическое объясне-
ние неоптимальности траектории CEM
1
, удовлетворяющей принципу
максимума.
Пример 13.6. Решить линейную задачу быстродействия, в которой
n =2, t
0
=0, U = S
1
(0),
A =
01
−10
,M
0
= S
π
(0),M
1
= {x ∈ E
2
: x
1
=3π, |x
2
| π}.
Множество достижимости X(t)=X(0,t,M
0
)=S
π+t
(0) впервые
прикоснётся к множеству M
1
вмоментвремениt = t
1
=2π вточке
x(t
1
)=
3π
0
,причёмψ(t
1
)=
1
0
(см. рисунок 13.17).
138
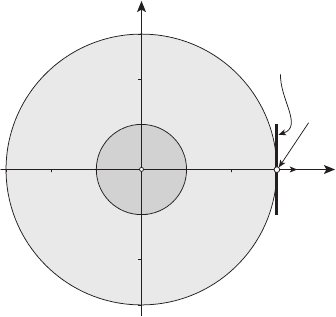
Имеют место следующие соотношения:
ψ(t)=e
−tA
∗
ψ(0),
u(t
1
)=ψ(2π)=ψ(0) =
1
0
,
u(t)=ψ(t); x(0) = πψ(0);
x(t
1
), −ψ(t
1
)
= −3πψ
1
(t
1
)+π |−ψ
2
(t
1
)|,
x(0) =
π
0
– начальная точка траектории x(t),
x(t
1
)=
3π
0
– конечная точка траектории x(t),
x(t)=(π + t) e
tA
ψ(0) = (π + t)
cos t
−sin t
,
u(t)=ψ(t)=
cos t
−sin t
,
здесь 0 t t
1
=2π.
x
1
x
2
0
π 2π 3π
−π
M
0
M
1
x(2π)
ψ(2π)
X(2π)
Рисунок 13.17
Оптимальная траектория в примере 13.6 изображена на рисунке
139
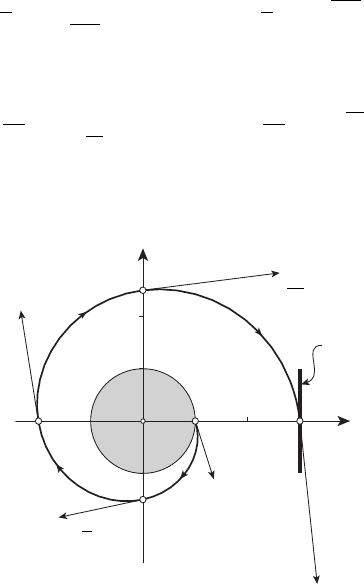
13.18;
x(0) =
π
0
, ˙x(0) =
1
π
,
x
π
2
=
0
−3π
2
, ˙x
π
2
=
−3π
2
−1
,
x(π)=
−2π
0
, ˙x(π)=
−1
2π
,
x
3π
2
=
0
5π
2
, ˙x
3π
2
=
5π
2
1
,
x(2π)=
3π
0
, ˙x(2π)=
1
−3π
.
x
1
x
2
π
π
0
2π 3π
−π
−π
−2π
M
0
M
1
˙x(0)
˙x
π
2
˙x(π)
˙x
3π
2
˙x(2π)
Рисунок 13.18
В заключение рассмотрим в примере 13.6 геометрическую интер-
претацию сопряжённой переменной ψ(t), множества достижимости
X(t) ≡ X(0,t,M
0
)=S
π+t
(0)
140
