Киселёв Ю.Н. Оптимальное управление
Подождите немного. Документ загружается.

x
1
x
2
0
−1
−2
−4
1
2
3
O
−3
O
−1
O
1
M
1
N
1
N
2
x
0
τ
t
1
− τ
u
2
= −1
u
2
= −1
I
−+
P
1
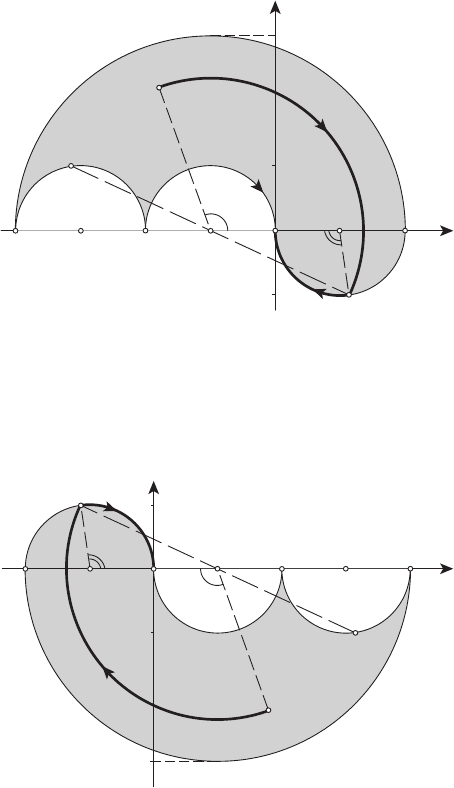
Рисунок 16.5
x
1
x
2
0
−1
−3
1
3
O
−1
O
1
M
1
M
3
N
1
x
0
τ
t
1
− τ
u
2
= −1
u
2
=+1
I
+−
Рисунок 16.6
161
область I
+−+
отвечает управлениям вида
u
2
(t)=
⎧
⎪
⎨
⎪
⎩
+1, 0 t<τ
1
,
−1,τ
1
<t<τ
2
= τ
1
+ π,
+1,τ
2
<t t
1
,
0 <τ
1
<π, 0 <t
1
− τ
2
<π;
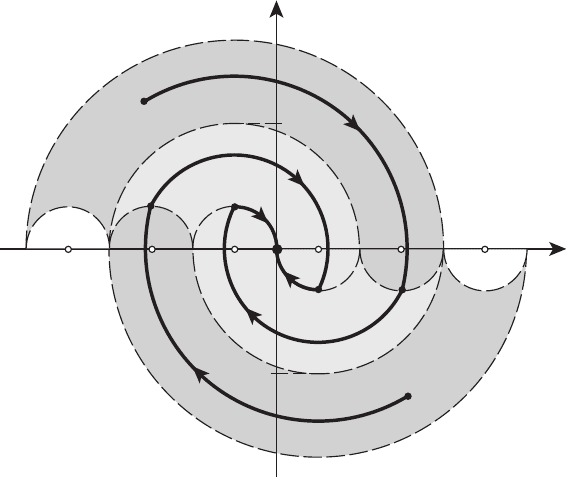
(см. рисунок 16.7).
x
1
x
2
0
−1
−3
−3
−4
1
3
3
5
O
−1
O
1
M
1
M
2
M
3
N
1
N
2
N
3
x
0
I
−+
I
+−
I
−+−
I
+−+
Рисунок 16.7
Для описания окончательного результата на фазовой плоскости
выделяется линия
...N
3
N
2
N
1
OM
1
M
2
M
3
...,
162
называемая линией переключения. Определим функцию
v(x
1
,x
2
)=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
−1, если точка (x
1
,x
2
) лежит выше
линии переключения ...N
2
N
1
OM
1
M
2
...
или на кривой N
1
O;
+1, если точка (x
1
,x
2
) лежит ниже
линии переключения или на кривой M
1
O.
Любая оптимальная траектория состоит из дуг окружностей с цен-
тром в точке O
−1
, лежащих выше линии переключения, где u
2
= −1,
и из дуг окружностей с центром в точке O
1
, лежащих ниже линии
переключения, где u
2
=+1.Функцияv(x
1
,x
2
) реализует синтез оп-
тимального управления (см. рисунок 16.8).
x
1
x
2
0
O
1
O
−1
M
1
M
2
M
3
M
4
N
1
N
2
N
3
N
3
u
2
= −1
u
2
=+1
Рисунок 16.8
Переход в начало координат возможен из любой точки x
0
=
a
b
фазовой плоскости. Построенные траектории, удовлетворяющие прин-
163
ципу максимума, оптимальны по быстродействию, см. раздел 3.15,
пример 15.1. Пример 16.1 подробно рассмотрен в книге [1].
Упражнение 16.1. Построить семейство изохрон в примере 16.1.
Пример 16.2. Построить синтез в начало координат для объекта
˙x
1
= x
2
,
˙x
2
= x
1
+ u
2
, |u
2
| 1.
(5)
Особенность рассматриваемой задачи заключается в том, что по-
падание в начало координат возможно не из любых начальных состоя-
ний x
0
фазовой плоскости, а лишь из начальных состояний, лежащих
вполосе
|x
1
+ x
2
| < 1.
Рассматриваемая система (5) при u
2
=0принимает вид
˙x
1
= x
2
,
˙x
2
= x
1
.
(6)
Система (6) имеет единственное положение равновесия (0, 0) типа
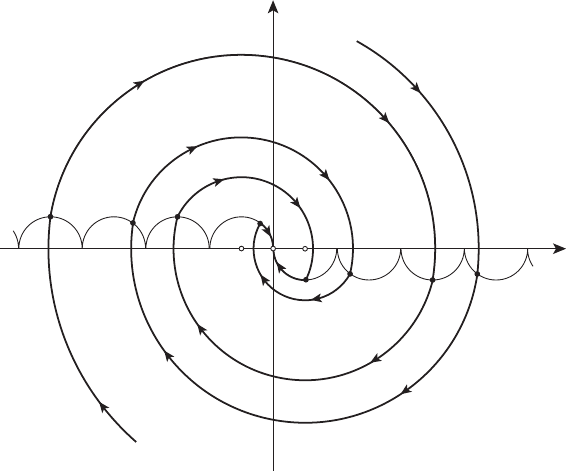
седло (неустойчиво по Ляпунову). Фазовые траектории этой системы
изображены на рисунке 16.9.
На основании принципа максимума приходим к выводу, что управ-
ление u
2
(t), удовлетворяющее принципу максимума, принимает лишь
значения ±1 и имеет не более одной точки переключения. Оптималь-
ные траектории рассматриваемой системы склеиваются из траекторий
системы (5) при u
2
=+1и u
2
= −1. Последние получаются из тра-
екторий системы (5), изображённых на рисунке 16.9, путём перено-
са положения равновесия в точки (−1, 0) и (+1, 0) соответственно.
Окончательный вид оптимальных траекторий в примере 16.2 показан
нарисунке16.10.
Синтезирующая функция
v(x
1
,x
2
)=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
−1, если точка (x
1
,x
2
) лежит выше линии переклю-
чения AOB вполосе|x
1
+ x
2
| < 1 инаBO,
+1, если точка (x
1
,x
2
) лежит ниже линии переклю-
чения AOB вполосе|x
1
+ x
2
| < 1 инаAO,
определена в полосе |x
1
+ x
2
| < 1.
Упражнение 16.2. Провести полное обоснование решения при-
мера 16.2. Показать, что из любой точки x
0
фазовой плоскости, не
164
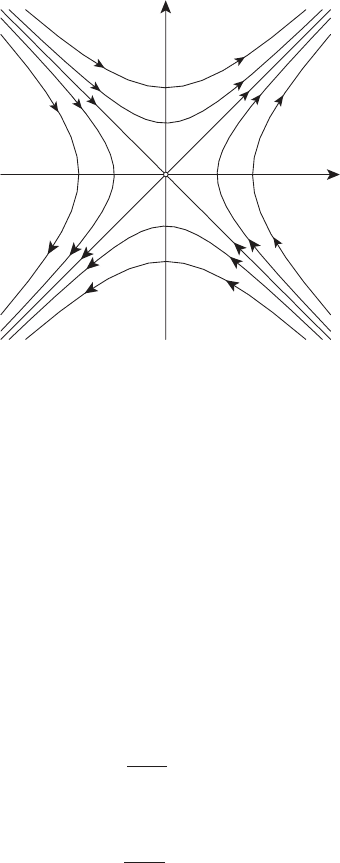
x
1
x
2
0
Рисунок 16.9
принадлежащей полосе |x
1
+ x
2
| < 1, невозможно попасть в начало
координат при помощи допустимого управления.
Упражнение 16.3. Построить семейство изохрон в примере 16.2.
Пример 16.3. Решить линейную задачу быстродействия
˙x = u, x, u ∈ E
n
,M
0
= {x
0
},M
1
= {0},U= S
1
(0),t
0
=0,
t
1
→ min .
Показать, что оптимальное время
t
1
опт
= x
0
,
оптимальное управление
u
опт
(t)=−
x
0
x
0
, 0 t x
0
,
а оптимальная траектория
x
опт
(t)=
1 −
t
x
0
x
0
, 0 t x
0
.
Найти сопряжённую переменную, участвующую в формулировке
принципа максимума.
165
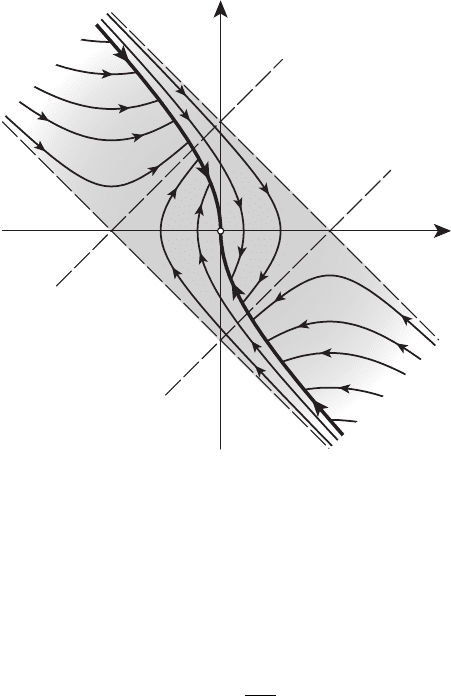
x
1
x
2
0
1
1
−1
−1
A
B
u
2
=+1
u
2
= −1
Рисунок 16.10
При n =2на рисунке 16.11 показаны оптимальные траектории,
ведущие в начало координат.
Упражнение 16.4. Установить единственность оптимального уп-
равления в примере 16.3. Показать, что синтезирующая функция v(x)
определяется формулой
v(x)=−
x
x
.
Упражнение 16.5. Построить синтез в примерах
a) ˙x = u; x, u ∈ E
2
; M
1
= S
1
(0),U= K ≡
x ∈ E
2
|x
1
| 1
|x
2
| 1
;
б) ˙x = u; x, u ∈ E
2
; M
1
= K, U = S
1
(0);
в) ˙x = u; x, u ∈ E
2
; M
1
= K, U = K;
г) ˙x = u; x, u ∈ E
2
; M
1
= S
1
(0),U= S
1
(0).
Исследовать вопрос о единственности решения, провести обоснова-
166
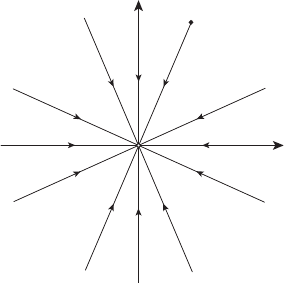
x
1
x
2
0
x
0
Рисунок 16.11
ние оптимальности.
167

4 Линейная задача быстродействия с “глад-
кой” областью управления. Численные
методы решения линейной задачи быст-
родействия
4.17 Теорема об опорной точке строго выпуклого
компакта и градиенте его опорной функции.
Теоремы единственности
Рассмотрим в пространстве E
n
непустой выпуклый компакт
U ∈ conv Ω(E
n
).
Этот компакт однозначно определяется своей опорной функцией
3
c(ψ) = max
u∈U
(u, ψ),ψ∈ E
n
. (1)
Возьмём любой отличный от нуля вектор ψ
0
∈ E
n
. Гиперплоскость
Γ
ψ
0
=
%
x ∈ E
n
:(x, ψ
0
)=c(ψ
0
)
&
называется опорной гиперплоскостью компакта U внаправлении
вектора ψ
0
. Множество
H
ψ
0
= U
"
Γ
ψ
0
называется опорным множеством компакта U в направлении век-
тора ψ
0
, см. рисунок 17.1.
Ясно, что
H
ψ
0
=
%
u ∈ U :(u, ψ
0
)=c(ψ
0
)
&
= ∅, (2)
т.е. опорное множество H
ψ
0
состоит из тех точек u ∈ U, на кото-
рых в соотношении (1) при ψ = ψ
0
достигается максимум. Опорное
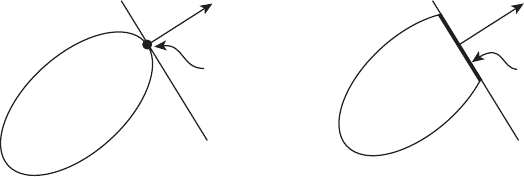
множество H
ψ
0
может состоять из одной точки, см. рисунок 17.1 а);
множество H
ψ
0
, изображённое на рисунке 17.1 б), состоит более чем
из одной точки.
3
Опорная функция (1), естественно, зависит от множества U;аргументU вобозна-
чении опорной функции здесь и ниже, для сокращения записи, будем опускать, если
из контекста понятно, об опорной функции какого множестве идёт речь.
168
U
U
ψ
0
ψ
0
Γ
ψ
0
Γ
ψ
0
H
ψ
0
H
ψ
0
а) б)
Рисунок 17.1
Определение 17.1. Выпуклый компакт U ∈ conv Ω(E
n
) называется
строго выпуклым в направлении ненулевого вектора ψ
0
∈ E
n
,если
опорное множество H
ψ
0
компакта U состоит из единственной точки.
Определение 17.2. Выпуклый компакт U ∈ conv Ω(E
n
) называется
строго выпуклым, если он является строго выпуклым в направлении
любого ненулевого вектора ψ
0
∈ E
n
.
Упражнение 17.1. Выяснить, какие из выпуклых компактов U яв-
ляются строго выпуклыми:
а) U = {u ∈ E
n
: u 1}≡S
1
(0) – единичный шар;
б) U = {u ∈ E
2
: |u
1
| 1, |u
2
| 1} –квадрат;
в) U = {u ∈ E
n
: u
∗
Qu 1} – компакт, ограниченный эллипсоидом,
Q = Q
∗
> 0 – симметричная положительно определённая матрица;
г) U =conv{a, b} – отрезок, соединяющий точки a и b; a, b ∈ E
n
.
Задача нахождения опорного множества возникает, например, при
использовании принципа максимума, и является некоторым элемен-
том решения задачи оптимального управления. Во многих примерах с
простым множеством U (отрезок, параллелепипед, шар и т.п.) задача
нахождения опорного множества решается, исходя из наглядных гео-
метрических соображений. Рассмотрим сейчас вопрос об аналитиче-
ском описании опорного множества H
ψ
0
для любого строго выпуклого
компакта. Следующая теорема содержит аналитическое условие стро-
гой выпуклости в терминах опорной функции c(ψ) и конструктивное
описание опорной точки при помощи градиента опорной функции.
Теорема 17.1. Пусть U ∈ conv Ω(E
n
), c(ψ) – опорная функция
169

выпуклого компакта U , H
ψ
0
– опорное множество компакта U вна-
правлении ненулевого вектора ψ
0
∈ E
n
.
A) Если в точке ψ
0
существует градиент c
(ψ
0
) опорной функ-
ции c(ψ), то опорное множество H
ψ
0
состоит из единственной
точки h
0
,причёмh
0
= c
(ψ
0
), т.е. опорная точка h
0
совпадает с
градиентом опорной функции в точке ψ
0
.
B) Если опорное множество H
ψ
0
выпуклого компакта U состоит
из единственной точки h
0
, то опорная функция c(ψ) имеет в
точке ψ
0
градиент c
(ψ
0
),причёмc
(ψ
0
)=h
0
.
2 Проверим сначала утверждение A). Возьмём произвольную точ-
ку u
0
∈ H
ψ
0
идокажем,что
u
0
= c
(ψ
0
). (3)
Этим будет закончено доказательство утверждения A).Чтобыустано-
вить (3), рассмотрим вспомогательную функцию
G(ψ)=c(ψ) − (ψ, u
0
).
Она удовлетворяет условиям
G(ψ
0
)=0, (4)
G(ψ) 0 ∀ψ ∈ E
n
. (5)
Равенство (4) вытекает из определения множества H
ψ
0
, см. (2). Нера-
венство (5) следует из определения опорной функции, см. (1), так как
u
0
∈ H
ψ
0
⊂ U. Условия (4), (5) влекут неравенство
G(ψ) G(ψ
0
) ∀ψ ∈ E
n
,
это означает, что функция G(ψ) имеет минимум в точке ψ
0
.Кроме
того, в точке ψ
0
функция G(ψ) имеет градиент
G
(ψ
0
)=c
(ψ
0
) − u
0
. (6)
Необходимое условие минимума G
(ψ
0
)=0, в силу (6), приводит к
равенству (3). Утверждение A) доказано.
Докажем теперь утверждение B) теоремы 17.1. Для этого сначала
установим существование такого вектора g ∈ E
n
,что
lim
λ→+0
c(ψ
0
+ λχ) − c(ψ
0
)
λ
=(χ, g) (7)
170
