Киселёв Е.С. Теплофизика правки шлифовальных кругов с применением СОЖ
Подождите немного. Документ загружается.


85
p
1
=
p
s
−
)
4
(
8
1
ж
ив
жs1
кж
s
rr
G
rr
HG
⋅⋅
⋅+⋅⋅
⋅⋅⋅
′
⋅
π
βµα
ρπ
, (92)
где
р
s
−
давление СОЖ на выходе из торцевого насадка, Па.
Для сечения на торцевой поверхности круга
р
1
=
р
s
.
Решив системы уравнений (91) и (92) при заданных давлениях
р
s
и
р
2
и размерах
r
1
,
r
2
,
r
s
методом последовательных приближений, определяют
G
ж
, а затем, используя
выражение (88),
−
радиальную скорость фильтрации
υ
r
.
2.1.3. Тепловое и гидродинамическое взаимодействие СОЖ с
кругом и правящим инструментом вне зоны их контакта
В тех случаях, когда СОЖ к зонам правки и шлифования движется сквозь поро-
вое пространство круга, используют однотемпературную модель взаимодействия жид-
кости с кругом как пористой средой, т.е.
Т
ж
=
Т
кр
.
Однако, если СОЖ подают к контактным зонам по внешним трактам (свободно
падающей или напорной струей к зоне резания и другими способами), для расчета
контактных температур необходимо определить коэффициенты теплопередачи от
жидкости к кругу
α
5
и от жидкости к алмазу правящего инструмента
α
2
. Кроме того,
для выполнения достаточно точных теплофизических расчетов необходимы сведения
о местонахождении и протяженности участков круга и правящего инструмента, нахо-
дящихся в контакте с СОЖ, а также значения коэффициента теплопередачи от воздуха,
приводимого в движение вращающимся шлифовальным кругом, к поверхностям круга
и правящего инструмента.
Наиболее просто коэффициенты теплопередачи от жидкости и воздуха определя-
ются с использованием эмпирических уравнений подобия.
Участок
АВ
круга (рис. 28) рассматриваем как участок пластины, продольно об-
текаемый потоком СОЖ с относительной скоростью
u
0
= (
ω
⋅ R
к
−
W
ж
) ,
где
W
ж
−
скорость истечения СОЖ из сопла:
W
ж
=
c
F
Q
; (93)
F
c
−
площадь выходного сечения сопла, м
2
.
Определим число Рейнольдса Re
"
:
µ
ρ
ν
АВ0жАВ0
""
"
⋅⋅
=
uu
Re
= (94)
где
"
АВ
- длина дуги
АВ
.
86
Если Re
"
≤
10
5
, то можно
определить коэффициент
теплопередачи в условиях обтекания
пластины ламинарным потоком по
эмпирическому уравнению подобия [96,
164, 166]:
250
430
50
Pr
Pr
PrRe660uN
,
w
f
,
f
,
f
f
,
⋅⋅=
"
, (95)
где
f
ff
f
f
f
C
;
ж
ж
ж
АВ
5
РruN
λ
µ
λ
α
=
⋅
=
"
;
f
f
u
;
C
νλ
µ
АВ0
жw
жww
w
ReРr
"
"
==
.
Параметры, в обозначениях
которых имеется индекс
f
, выбирают по тем-
пературе СОЖ на выходе из сопла, а
параметры с индексом
W
−
по
средней температуре поверхности круга на участке
АВ
;
α
5
−
среднее на участке
АВ
значение коэффициента теплопередачи, Вт/(м
2
⋅
К).
Если Re > 10
5
, то расчет ведут по эмпирическому уравнению подобия, получен-
ному для турбулентного режима течения:
250
43080
Pr
Pr
PrRe03610uN
,
w
f
,
f
,
ff
,
⋅⋅⋅=
"
. (96)
Расчетную схему для определения коэффициента теплопередачи от СОЖ к пра-
вящему инструменту примем как для случая поперечного обтекания цилиндра. Сред-
нее по поверхности правящего инструмента, обтекаемой СОЖ, значение коэффициен-
та теплопередачи
α
2
определим по эмпирическому уравнению подобия [96, 164, 166]:
250
w
nm
dcd
Pr
Pr
PrReuN
,
f
fff
L
⋅⋅⋅=
, (97)
где Re
f
d
=
f
W
ν
жd
;
f
f
d
ж
2
d
uN
λ
α
⋅
=
,
где
d
−
эквивалентный диаметр правящего инструмента, м;
L
c
,
m
,
n
−
числовые коэф-
фициенты, выбираемые в зависимости от диапазона чисел Re
f
d
: при Re
f
d
= 5 ... 10
3
;
L
c
=
0,5;
m
= 0,5;
n
= 0,38; при Re
f
d
> 10
3
L
c
= 0,25;
m
= 0,6;
n
= 0,43.
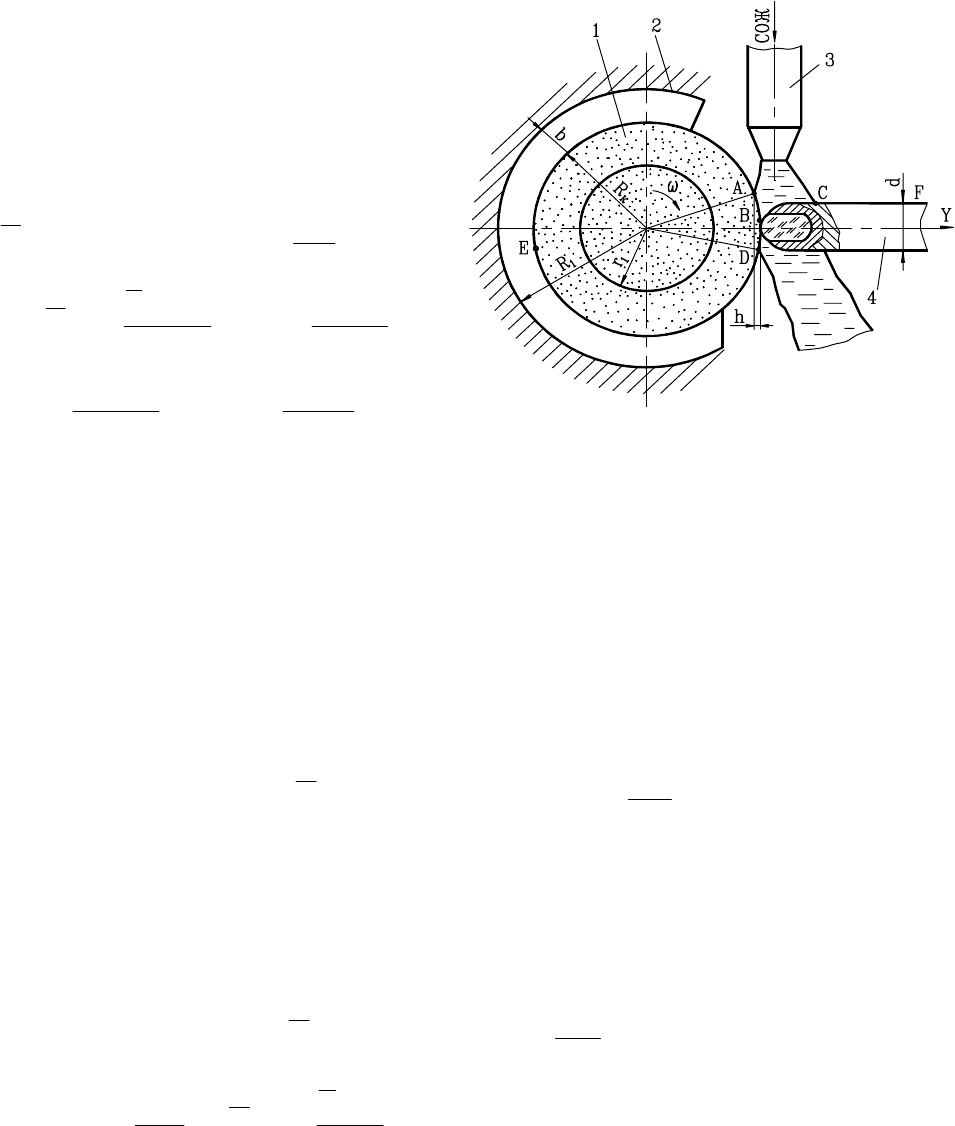
Для определения коэффициентов теплопередачи от воздуха к поверхности круга и
правящего инструмента считаем заданными приведенные на рис. 28
Рис. 28. Расчетная схема для определения ко-
эффициентов теплопередачи: 1
−
шлифоваль-
ный круг; 2
−
защитный кожух; 3
−
сопло для
подачи СОЖ; 4
−
правящий инструмент;
h
−
толщина пропитанного жидкостью слоя круга

87
размеры, частоту вращения круга, изменения скоростей воздушных потоков, генери-
руемых вращающимся кругом, вдоль координаты
Y
[
W
(
Y
)].
Для выбора эмпирических уравнений подобия воспользуемся данными работ
[96, 166]. Определим среднее значение коэффициента теплопередачи
α
6
от от воздуха,
приводимого в движение вращающимся кругом, к поверхности
АЕД
круга (см. рис.
28).
Уравнение подобия, обобщающее имеющиеся опытные данные [96, 166] по теп-
лопередаче от воздуха к поверхности вращающегося цилиндра, окруженного непод-
вижным кожухом, имеет вид:
для ламинарного режима течения (при
Т
a
< 41,2)
))1(
)(2
Nu
1
к3
1
к3
−
−
⋅+
⋅
=
R(bln
Rb
,
где
b
3
=
R
1
−
R
к
−
величина зазора между внутренней стенкой кожуха и рабочей по-
верхностью круга, м;
Т
а
=
в
ν
ω
⋅
b
3
1,5
⋅
R
к
0,5
−
число Тейлора;
в
36
2
Nu
λ
α
b⋅
=
−
число Нуссельта.
При расчетах теплофизические характеристики воздуха, необходимые для опре-
деления коэффициента теплопередачи
α
6
, примем для средней температуры воздуха в
зазоре
2
21
tt
t
f
+
=
,
где
t
1
−
температура на периферии круга, К;
t
2
−
температура на внутренней поверхно-
сти защитного кожуха, К.
Если известна поверхностная плотность теплового потока круга q
1
, коэффициент
теплопередачи
α
6
можно определить для данных условий по разнице температур (
t
1
−
t
2
):
21
1
6
tt
q
−
=
α
. (98)
Для ламинарного течения воздуха с макровихрями (при 41,2
≤
Т
a
≤
10
4
)
Nu = 0,42 (
T
a
2
⋅
Pr)
0,25
, (99)
где Pr = 0,7
−
число Прандтля для воздуха.
Для турбулентного режима течения воздуха с макровихрями (
Т
а
> 10
4
)
Nu = 0,032 (
T
a
2
⋅
Pr)
0,33
. (100)
По найденному значению Nu искомый коэффициент теплопередачи
α
6
найдем из
соотношения

88
3
в
6
2
Nu
b
λ
α
⋅
=
.
(101)
Определим коэффициент
α
4
теплопередачи от воздуха к корпусу правящего ин-
струмента по его максимальному значению, соответствующему условиям вынужден-
ного (поперечное обтекание воздухом цилиндра) и свободного (теплопередача от го-
ризонтального цилиндра) движения. В данном случае
α
4
−
это среднее значение ко-
эффициента теплопередачи на участке
СF
поверхности правящего инструмента (см.
рис. 28).
Число Нуссельта для условий вынужденного движения, показанных на рис. 28,
можно вычислить по зависимости
вf
f
d
λ
α
⋅
=
4
d
Nu . (102)
В то же время число Нуссельта можно определить с использованием чисел Рей-
нольдса Re
f
d
и Прандтля Pr
f
:
Nu =
L
c
⋅
nm
d
Pr
ff
Re ⋅
, (103)
где Re
f
d
=
f
d)Y(W
в
ν
;
λ
в
f
,
ν
в
f
−
соответственно коэффициенты теплопроводности и кине-
матической вязкости воздуха для температуры
t
f
;
W
(
Y
)
−
скорость воздуха вдоль коор-
динаты
Y
(по направлению продольной оси правящего инструмента), м/с;
L
c
,
m
,
n
−
ко-
эффициенты [96, 166].
Для Re
f
d
= 5 ... 10
3
L
c
= 0,5,
m
= 0,5,
n
= 0,38.
Для Re
f
d
> 10
3
L
c
= 0,25,
m
= 0,6,
n
= 0,43.
Коэффициент теплопередачи
d
ff
вd
4
uN
λ
α
⋅
=
. (104)
Для условий свободного движения число Нуссельта можно вычислить, исполь-
зовав одну из двух зависимостей:
вm
4
m
uN
λ
α
d⋅
=
; (105)
1
n
mc1m
Pr)(GruN
⋅=
L
, (106)
где Pr
m
,
λ
вm
−
соответственно число Прандтля и коэффициент теплопроводности для
воздуха при температуре
2
w
m
f
tt
t
+
=
;
t
dg
m
∆β
ν
⋅⋅
⋅
=
m
2
3
Gr
−
число Грасгофа, (107)

89
где
g
= 9,81
−
ускорение свободного падения, м/с
2
;
ν
m
−
кинематическая
вязкость воздуха при температуре t
m
, м/с;
mm
m
273
11
tT
+
==
β
−
коэффициент объемно-
го расширения воздуха, К
-1
;
∆
t
= (
t
w
−
t
f
)
−
температурный напор, К;
t
w
−
температура
поверхности правящего инструмента в рассматриваемом сечении по оси
Y
, К;
L
c1, n1
−
числовые коэффициенты, выбираемые для наших условий по данным работ [96,
166]:
при (Gr
⋅
Pr)
m
= 10
-3
... 5
⋅
10
2
L
c1
= 1,18,
n
1
= 0,125;
при (Gr
⋅
Pr)
m
= 5
⋅
10
2
... 2
⋅
10
7
L
c1
= 0,54.
n
1
= 0,25;
при (Gr
⋅
Pr)
m
= 2
⋅
10
7
...10
13
C
1
= 0,135,
n
1
= 0,33.
Коэффициент теплопередачи
α
4
для условий свободного движения
d
mвm
4
Nu
λ
α
⋅
=
. (108)
В дальнейшие расчеты закладывается большее значение
α
4
из найденных по за-
висимостям (104) и (108).
2.1.4. Тепловое и гидродинамическое взаимодействие СОЖ
с кругом и правящим инструментом в зоне правки
Результаты анализа работ [35 – 37, 42, 165] позволяют утверждать, что основным
путем транспортирования СОЖ в контактные зоны при шлифовании и правке является
поровое пространство шлифовального круга.
Образующийся в зоне контакта круга с алмазом тепловой поток можно рассчи-
тать по следующему выражению [118]:
Q
=
P
zn
⋅
ω
⋅
R
к
. (109)
В свою очередь
Q
=
Q
к
+
Q
a
, (110)
где
Q
к
,
Q
a
−
тепловой поток, отводимый соответственно в круг и в правящий инстру-
мент, Вт.
Q
к
в свою очередь разделяется на две составляющие: тепловой поток
Q
к1
, по-
глощаемый СОЖ, находящейся в поверхностном слое круга, Вт; тепловой поток
Q
к2
,
передаваемый вглубь круга, Вт:
Q
к
=
Q
к1
+
Q
к2
. (111)
Значения
Q
к2
и
Q
a
можно найти численным интегрированием дифференциальных
уравнений теплопроводности круга (71), (80) и алмаза (60). Поэтому для получения
математической модели теплового и гидродинамического взаимодействия СОЖ, круга
и правящего инструмента в зоне их контакта необходимо прежде всего определить
значение
Q
к1
.
При подаче СОЖ к зоне правки поливом толщина
h
слоя круга, пропитанного
жидкостью (см. рис. 28), определяется из условия равенства капиллярного напора

90
жидкости
∆
Р
к
и напора
∆
Р
ц
,
обусловленного действием центробежных
сил на жидкость, находящуюся во вращающемся круге:
к
2
кс
ц
0
n
0
к
2
cos
2
R
hV
Р;
R
Р
⋅⋅
=⋅=
ρ
∆θ
σ
∆
. (112)
Из (112) при условии
∆
Р
к
=
∆
Р
ц
следует ранее приведенная зависимость (37) для
определения глубины пропитки
h
вращающегося круга при подаче СОЖ поливом.
В дальнейшем будем рассматривать круг как пористое тело, имеющее две зоны:
I
зона: 0
≤
2
r
i
≤
(2
R
к
−
2
h
)
−
круг с порами, заполненными воздухом (
r
i
−
текущий ра-
диус круга). Для этой зоны все теплофизические свойства круга определяют по зави-
симостям, приведенным в пунктах 2.1.1
−
2.1.3, как для сухого круга без пор;
II
зона:
2
R
к
−
2
h
<2
r
i
≤
2
R
к
−
круг с порами, заполненными СОЖ. Соответственно, все тепло-
физические свойства круга можно определить по зависимостям, приведенным в пара-
графах 2.1
−
2.3, как для круга, пропитанного СОЖ.
Тепловое состояние круга можно оценить по результатам численного интегри-
рования рабочих уравнений и краевых условий, приведенных в пункте 2.1.1. По ре-
зультатам расчета находим радиус
R
s
расположения точки, в которой температура кру-
га достигает температуры кипения СОЖ Т
s
.
Если окажется, что (
R
к
−
R
s
)
≤
h
, то в точке
r
=
R
s
формируются собственные гра-
ничные условия:
r
=
R
s
;
T
=
T
s
. (113)
При этом величину
Q
к1
определим методом последовательных приближений по
соотношению
Q
к1
=
q
к1
⋅
F
к
, (114)
где
q
к1
=
q
к
−
q
Rs
;
q
к
−
поверхностная плотность теплового потока на периферии круга
радиусом
R
к
, Вт/м
2
:
q
к
=
к
к
F
Q
;
q
Rs
−
поверхностная плотность теплового потока на радиусе круга
r
=
R
s
, Вт/м
2
:
r
t
q
∂
∂
λ
кRs
−=
;
F
к
−
номинальная площадь контакта круга с алмазом, м
2
.
В случае использования в качестве правящего инструмента алмазного карандаша
величину
Q
к
удобнее вычислить по зависимости
Q
к1
= 2
π
⋅R
к
⋅n
x
⋅d
a
⋅
ρ
ж
⋅П
⋅
L
⋅
ω
⋅
∆
, (115)
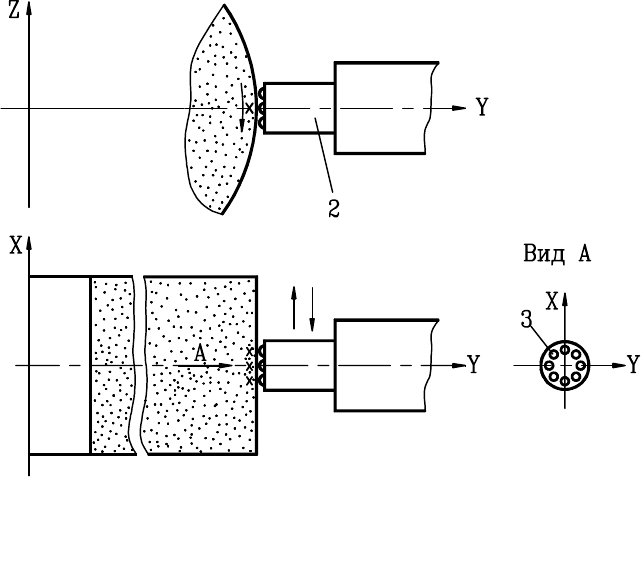
91
Рис. 29. Схема правки круга алмазными карандашами ти-
пов 02, 03, 04 ГОСТ 607-80 Е: 1
−
круг; 2
−
алмазный ка-
рандаш; 3
−
алмаз
где
∆
= min
−
sк
RR
h
, м;
d
a
−
диаметр алмазного
зерна, м;
n
x
−
количество
алмазных зерен правя-
щего карандаша, одно-
временно контактирую-
щих с кругом (
z
= 0,
y
=
R
к
, см. рис. 29).
Температуру по-
верхности круга
Т
к
в зо-
не его контакта с зерном
алмаза можно опреде-
лить путем численного
интегрирования уравне-
ния теплопроводности
(71) при уточненном
значении
Q
к2
:
Q
к2
=
Q
−
Q
a
−
α
5
⋅
(
Т
к
−
Т
ж
)
⋅F
к
⋅П
. (116)
Если при определении
R
s
окажется, что (
R
к
-
R
s
) >
h
, то
Q
к2
=
Q
−
Q
a
−
2
π⋅
R
к
⋅
h
⋅
H
к
⋅ρ
ж
⋅
L
⋅ω⋅
П
. (117)
При подаче СОЖ к зоне правки через поры круга с помощью полуоткрытых
клиновых насадков, расположенных с торцев круга, методика расчета сохраняется за
исключением выражения (37): высота
h
в этих условиях определяется местом распо-
ложения полуоткрытых клиновых насадков для подачи СОЖ.
В рассмотренной последовательности расчетов отсутствуют зависимости, опи-
сывающие интенсивность теплопередачи в СОЖ при ее кипении. Это связано с тем,
что кипение СОЖ теоретически возможно в данном случае не в большом объеме, а
лишь в капиллярно-пористой структуре с очень развитой поверхностью соприкосно-
вения жидкости с кругом, отличающимся высокой пористостью. В таких условиях ин-
тенсивность теплопередачи очень высока и процессы испарения СОЖ лимитируются
не интенсивностью теплопередачи от круга к жидкости, а интенсивностью тепловыде-
ления в зоне контакта и интенсивностью теплопроводности круга. Поэтому для этого
случая принята однотемпературная модель (температура пористого шлифовального
круга принимается равной температуре пропитывающей его жидкости).
Алгоритм расчета температурных полей объектов, контактирующих при правке
точением, приведен в работе [51].
2.2. Тепловое взаимодействие круга и алмазного правящего
92
инструмента при правке шлифованием
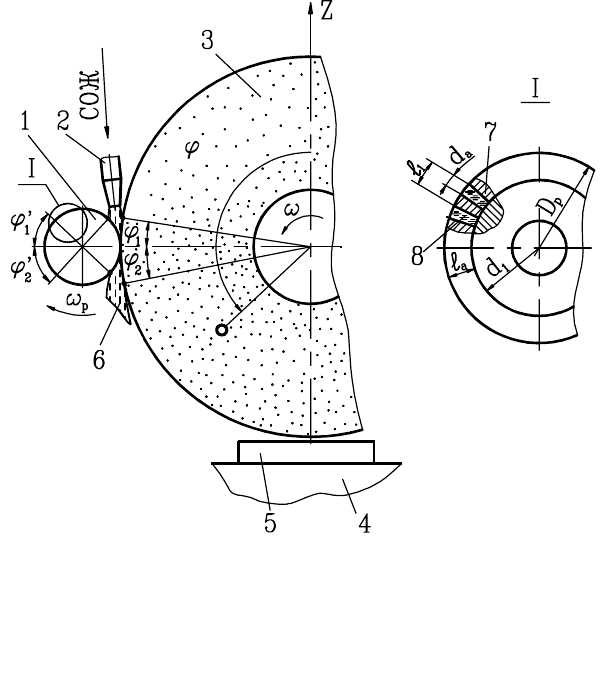
Правка шлифованием в современном машиностроении осуществляется в основ-
ном алмазными роликами (рис. 30).
Предполагается, что поверхность ролика после доводки является гладкой. Алмаз-
ные зерна вкраплены в связку (медь, сплав меди с никелем). В радиальном направле-
нии ролик условно разделен на две зоны:
- наружный слой толщиной
"
а
(
"
а
−
средний размер алмазных зерен в радиальном
по отношению к ролику направлении);
- остальная часть или корпус алмазного правящего ролика.
Для расчета теплового
состояния ролика использу-
ем дифференциальное урав-
нение теплопроводности, за-
писанное в неподвижной ци-
линдрической системы ко-
ординат (см. рис. 30). По ви-
ду уравнение теплопровод-
ности ролика одинаково с
аналогичным уравнением
теплопроводности шлифо-
вального круга (70), (71).
При этом температурное по-
ле считаем стационарным,
двумерным.
При моделировании
температурного поля в на-
ружном слое алмазного ро-
лика примем однотемпера-
турную модель (то есть для
каждой узловой точки температура в алмазном зерне и в связке считается одинаковой).
Для алмазного зерна, находящегося в контакте с а.з., определим температурное поле.
При этом для расчета теплового потока в радиальном направлении используем коэф-
фициенты теплопроводности алмаза, как функции температуры. Для расчета теплово-
го потока в окружном направлении примем наружный слой алмазного ролика сплош-
ным со следующими теплофизическими свойствами: коэффициент теплопроводности
λ
эф
=
λ
а
⋅
ε
эф
+
λ
с
⋅
(1
−
ε
эф
) ; (118)
произведение плотности на удельную теплоемкость (
ρ
⋅с
)
эф
:
ρ
а
⋅
с
а
⋅
ε
эф
+
ρ
с
⋅
с
с
(1
−
ε
эф
), (119)
где
ε
эф
=
d
а
⋅
(
"
1
)
-1
(см. рис. 30).
Рис. 30. Схема правки круга алмазным правящим роли-
ком: 1
−
алмазный ролик; 2
−
сопло; 3
−
шлифовальный
круг; 4
−
стол; 5
−
заготовка; 6
−
поток СОЖ; 7
−
связка
ролика; 8
−
алмазное зерно
93
Температурное поле в остальной части алмазного ролика (корпуса)
моделируем обычным путем решения уравнения теплопроводности для сплошной сре-
ды.
При определении граничных условий теплообмена на наружной поверхности
правящего ролика примем допущение: из-за малых размеров и существенно меньшей
рабочей скорости правящего ролика по сравнению с размерами и рабочей скоростью
шлифовального круга можно не учитывать влияние вращающегося ролика на интен-
сивность воздушных потоков.
Как установлено исследованиями Л.В.Худобина и С.В.Семенова [123, 124, 153],
эпюры скоростей воздушных потоков, генерируемых кругом, при введении в рабочую
зону вращающегося алмазного ролика несколько изменяются. Однако расчет коэффи-
циентов теплопередачи показывает, что этими изменениями при исследовании тепло-
вого взаимодействия круга и ролика можно пренебречь. Поэтому при расчете коэффи-
циентов теплопередачи для зоны
ϕ
′
2
<
ϕ
<
ϕ
′
1
(см. рис. 30) с целью упрощения исполь-
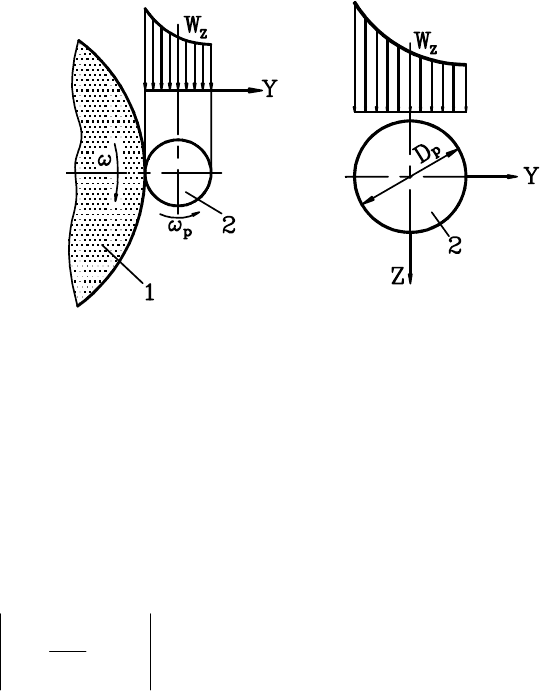
зуем схему, соответствующую обтеканию неподвижного цилиндра (рис. 31).
Коэффициент теплопередачи
α
9
определяется зависимостями (104) и (108). Од-
нако число Рейнольдса Re
f
d
рассчитаем по скорости воздуха
W
z
вцентре
ролика и диаметру
D
p
(cм. рис. 31). В
качестве определяющего размера при расчете
чисел Грасгофа и Нуссельта
(зависимости (105), (106)) также примем
D
р
.
Коэффициент теплопередачи
α
9
будем считать одинаковым для всей по-
верхности ролика, заключенной внутри
сектора
ϕ
′
2
<
ϕ
<
ϕ
′
1
.
При расчете коэффициентов
теплопередачи в секторе
ϕ
′
1
≥
ϕ
≥
ϕ
′
2
учтем
окружную скорость ролика;
α
2
рас-
считаем по тем же зависимостям (95), (96), что и для круга, но с подстановкой в эти
зависимости параметров, соответствующих алмазному ролику.
В качестве скорости
u
0
при расчете числа Рейнольдса Re
"
по зависимости (94)
примем ее значение
u
0
=
ж
p
p
2
W
D
−⋅
ω
, (120)
Рис. 31. Схема обтекания воздушными
потоками, генерируемыми вращаю-
щимся шлифовальным кругом (1), ци-
линдрического алмазного ролика (2)
94
как и необходимость учета в расчетах зависимости теплофизических свойств контак-
тирующих объектов от температуры, ограничивает возможность использования анали-
тических методов решения уравнений теплопроводности (классического, операцион-
ного, источников). Поэтому, учитывая нежелательность использования упрощенной
трактовки математической модели процесса, в нашем случае было неизбежно обраще-
ние к численным методам решения задач тепло-массообмена. Однако, численные ме-
тоды расчета теплового состояния, дающее хорошие результаты при решении уравне-
ний теплопроводности для вращающихся объектов Д.Ши [163] (в нашем случае
−
правка круга шлифованием и круглое наружное шлифование заготовок), оказываются
неприемлемыми для системы контактирующих объектов, один из которых движется
поступательно и не вращается, а другой вращается (правка точением, плоское шлифо-
вание). Это обусловлено тем, что для совместного интегрирования дифференциальные
уравнения теплопроводности взаимодействующих объектов должны быть записаны в
неподвижной системе координат. В этом случае уравнение теплопроводности для
вращающегося объекта принимает вид, отличный от того, который соответствует нев-
ращающемуся или вращающемуся объекту при его записи в жестко связанной с этим
объектом системе координат [163]. В связи с этим, для расчетов теплового состояния
системы контактирующих объектов при правке круга шлифованием и круглом наруж-
ном шлифовании заготовок можно воспользоваться известными приемами численного
решения задач теплообмена (например работой [163]). Для правки точением попыта-
емся найти приемлемую методику, учитывающую указанные несоответствия и обес-
печивающую для широкого диапазона граничных условий реального процесса правки
достаточно высокую точность расчетов теплового состояния системы вращающегося и
движущегося поступательно невращающегося объектов при их механическом контак-
те. Методику решения подобных задач, вероятно, можно будет использовать не только
для анализа теплового состояния контактирующих объектов при правке точением, но и
для большинства операций лезвийной обработки, для описания теплового состояния
тормозных устройств фрикционного типа, при анализе аварийных ситуаций в момент
касания деталями ротора (например, лопатками газотурбинных насосов и двигателей)
поверхности статора и т.п. Учитывая перечисленные обстоятельства, несколько рас-
ширим условия правки кругов точением и включим в их число не только правку ал-
мазными карандашами и алмазами в оправе, но и правку алмазными пластинами.
Адекватность полученных во второй главе математических моделей, правиль-
ность выбранных граничных условий и методов численного решения уравнений теп-
лопроводности на ПЭВМ проверим путем сопоставления результатов численных ре-
шений и прямых экспериментальных исследований с результатами измерения кон-
тактных температур при правке кругов точением и шлифованием и шлифовании заго-
товок с непрерывной правкой круга.
С целью сокращения объема математических выкладок рассмотрим возможность
создания методики численного решения уравнений теплообмена системы вращающе-
гося шлифовального круга и правящего инструмента, движущегося поступательно, на
примере правки круга без применения СОЖ правящими инструментами, имеющими
