Киселёв Е.С. Теплофизика правки шлифовальных кругов с применением СОЖ
Подождите немного. Документ загружается.

75
вывод основных рабочих уравнений
Тепловое взаимодействие контактирующих объектов при правке круга и шлифо-
вании заготовок рассмотрим поэтапно:
1) Изучение теплового взаимодействия круга и правящего инструмента при
правке точением [54 – 56].
Здесь важно правильно выбрать граничные условия контактного взаимодействия
и получить основные рабочие уравнения теплопроводности. Учитывая высокую эф-
фективность транспортирования СОЖ к зонам обработки по внутренним трактам и
недостаточную изученность влияния жидкости на тепловой баланс как при правке, так
и при шлифовании, необходимо рассмотреть гидродинамику СОЖ при движении ее
сквозь поровое пространство вращающегося шлифовального круга в общем виде, пока
без изучения частных вопросов фильтрации. Для расчета контактных температур при
правке необходимо определить коэффициенты теплопередачи от жидкости к кругу и
алмазу, уточнить сведения о местоположении и протяженности участков круга и пра-
вящего инструмента, находящихся в контакте с СОЖ, а также значения коэффициен-
тов теплопередачи от воздуха, приводимого в движение вращающимся кругом, к кругу
и правящему инструменту. При этом коэффициенты теплопередачи следует опреде-
лить как для зоны контакта, так и вне ее.
2) Изучение особенностей теплового взаимодействия круга и правящего инстру-
мента при правке шлифованием, определение граничных условий и коэффициентов
теплопередачи [54 – 56].
3) Исследование тепловых взаимодействий круга, правящего инструмента и за-
готовки при шлифовании с непрерывной правкой круга.
Контакт круга с заготовкой обладает внешними признаками его контакта с пра-
вящим роликом. Наиболее существенно различие в значениях окружных скоростей
ролика и заготовки.
В отличие от изучаемых на первом и втором этапах процессов правки круга то-
чением и шлифованием, в исследованиях третьего этапа в рассмотрение вводится вто-
рая зона контакта круга (с заготовкой), что вносит изменения в тепловой баланс как
процесса правки, так и процесса шлифования. Учитывая, что этот случай является
наиболее общим (при отсутствии шлифования заготовки
−
правка шлифованием, при
отсутствии правки
−
шлифование заготовки), приемы и результаты изучения процесса
шлифования с непрерывной правкой круга можно будет в дальнейшем использовать
для раздельного изучения процессов правки и шлифования с применением СОЖ.

76
4) Выявление возможностей и путей использования особенностей
движения СОЖ сквозь поровое пространство вращающегося шлифовального круга в
целях повышения эффективности операций шлифования.
Схема правки круга точением показана на рис. 25.
Рис. 25. Схема правки круга однокристальным правящим инструментом: 1
−
шлифовальный
круг; 2
−
сопло; 3
−
поток СОЖ; 4
−
связка; 5
−
кристалл алмаза; 6
−
корпус
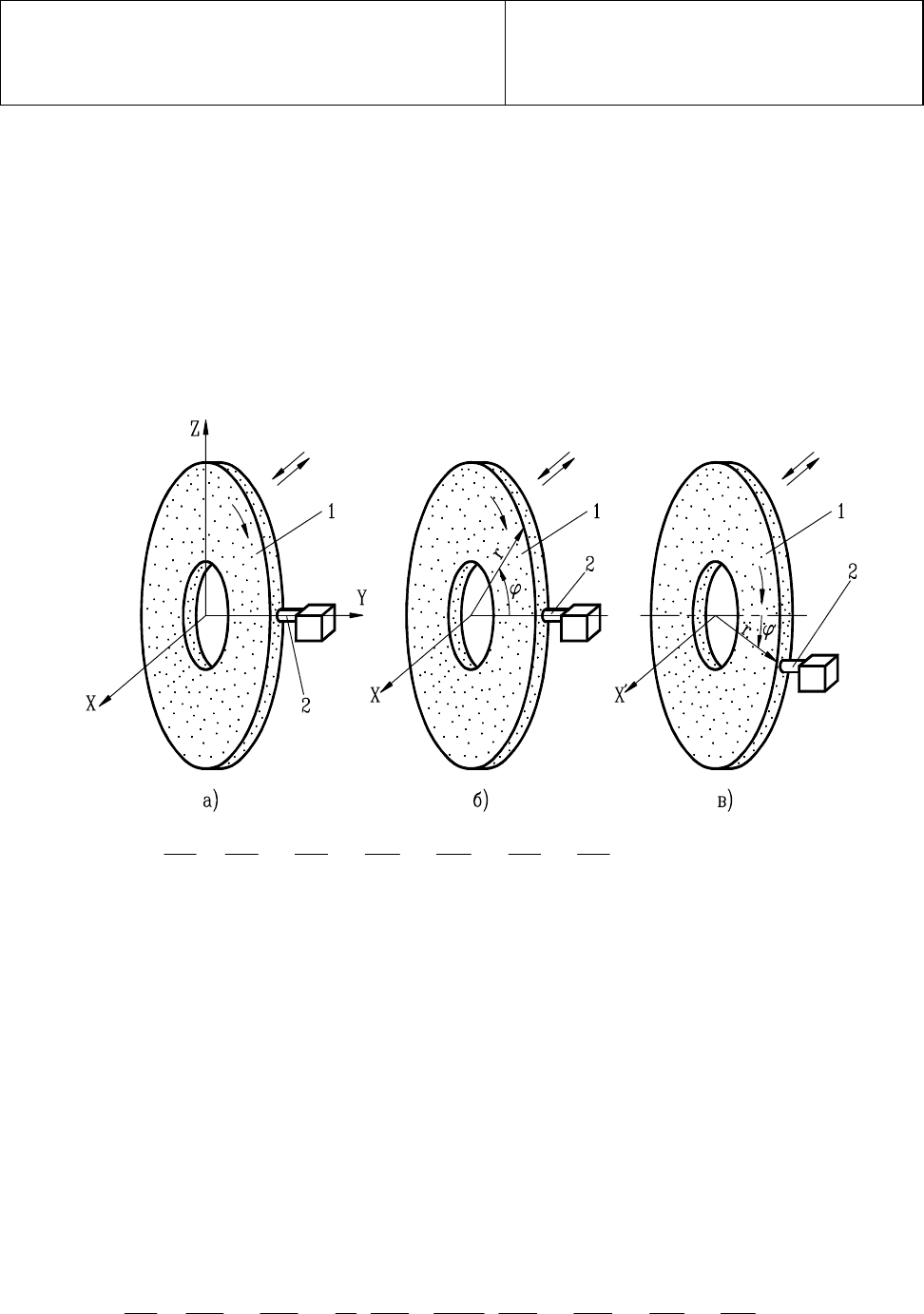
Процесс правки рассмотрим в следующих системах координат:
Шлифовальный круг Правящий инструмент
1.
Х
,
Y
,
Z
(неподвижная относительно пра-
вящего инструмента, декартова, рис. 26, а)
1.
Х
,
Y
,
Z
(неподвижная, декартова,
рис. 26, а)
2.
r
,
ϕ
,
Х
(неподвижная относительно пра-
вящего инструмента, цилиндрическая, рис.
26, б)
2.
r′
,
ψ
,
Y
(неподвижная, цилинд-
рическая, рис. 25)
77
3.
r
,
ϕ
′
,
Х′
(подвижная относительно пра-
вящего инструмента, цилиндрическая, рис.
26, в)
Рис. 26. Системы координат при правке шлифовального круга однокристальным пра-
вящим инструментом: а) неподвижная относительно правящего инструмента, декарто-
ва; б) неподвижная цилиндрическая; в) подвижная цилиндрическая; 1
−
шлифоваль-
ный круг; 2
−
правящий инструмент
Для каждого из элементов правящего инструмента (алмаз, связка, корпус) диф-
ференциальное уравнение теплопроводности можно представить в следующем виде:
а) декартова система координат
v
q
z
t
zy
t
yx
t
x
t
с +
+
+
=⋅⋅
∂
∂
λ
∂
∂
∂
∂
λ
∂
∂
∂
∂
λ
∂
∂
τ∂
∂
ρ
, (58)
где
t
−
текущая температура, К;
τ
−
время, с;
λ
=
λ
(
t
)
−
теплопроводность, Вт/(м
⋅
К);
с
=
с
(
t
)
−
удельная теплоемкость, Дж / (кг
⋅
К);
ρ
=
ρ
(
t
)
−
плотность, кг/м
3
.
В отличие от известных работ по теплофизике процессов шлифования и правки
[33, 34, 91, 122, 127, 167] в уравнении (58) и во всех последующих уравнениях тепло-
проводности учтена зависимость теплофизических свойств взаимодействующих объ-
ектов (
λ
,
с
,
ρ
и др.) от температуры. В связи с этим дифференциальные уравнения теп-
лопроводности являются нелинейными, а их решение возможно только численными
методами [117, 118, 163] (см. главу 3).
б) Цилиндрическая система координат (см. рис. 25):
()
v
q
y
t
y
t
r
r
t
rr
t
r
t
с +
+
⋅
′
+
′
⋅
′
+
′′
=⋅⋅
∂
∂
λ
∂
∂
ψ∂
∂
λ
ψ∂
∂
∂
∂λ
∂
∂
λ
∂
∂
τ∂
∂
ρ
2
1
. (59)
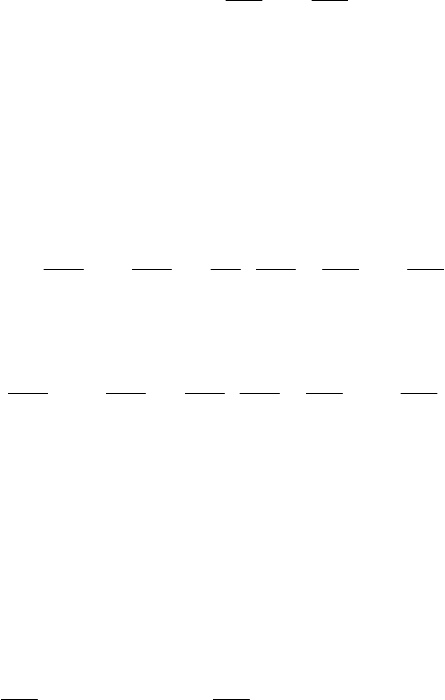
78
Для отдельных элементов правящего инструмента
дифференциальное уравнение теплопроводности можно упростить. Так за малостью
размеров поперечного сечения кристалла алмаза можно принять, что температура на
каждой элементарной площади сечения распределена равномерно [41, 89, 96, 117, 127,
130]. Тогда температурное поле кристалла алмаза можно считать одномерным, ста-
ционарным. В этом случае уравнение теплопроводности представим в следующем ви-
де:
0
va
=+
q
y
td
y
∂
λ
∂
∂
. (60)
Температурные поля связки и корпуса правящего инструмента, учитывая незна-
чительные изменения температуры по направлению
ψ
(см. рис. 25), примем двухмер-
ными стационарными (осесимметричными) без внутренних источников тепла [41, 89,
96, 117, 127, 130].
Тогда для связки
0
c
c
c
=
+
′
⋅
′
+
′′
y
t
yr
t
rr
t
r
∂
∂
λ
∂
∂
∂
∂
λ
∂
∂
λ
∂
∂
, (61)
а для корпуса правящего инструмента
0
кo
кo
кo
=
+
′
⋅
′
+
′′
y
t
yr
t
rr
t
r
∂
∂
λ
∂
∂
∂
∂
λ
∂
∂
λ
∂
∂
. (62)
В уравнениях (60)
−
(62)
λ
с
и
λ
ко
−
соответственно теплопроводность связки и
корпуса правящего инструмента.
Из бесчисленного количества ситуаций, описываемых уравнениями (58)
−
(62),
выделим граничными условиями описание условий теплообмена контактирующих
объектов при правке с окружающей средой. В зоне контакта алмаза с кругом (
y
=
R
к
)
Т
ал
=
Т
кр
; (63)
v0н0жжн2на
кк
qуFtGCF
y
t
F
y
td
RyRy
⋅⋅=⋅⋅+⋅
−⋅
−+
==
∆∆
∂
∂
λ
∂
λ
, (64)
где
Т
ал
и
Т
кр
−
температура соответственно алмаза и круга, К;
у
=
+
к
R
и
у
=
−
к
R
−
коор-
динаты соответственно зоны контакта со стороны алмаза и со стороны круга, м;
∆
t
0
−
подогрев СОЖ при прохождении через зону контакта, К.
Таким образом, отличительной особенностью приведенных зависимостей являет-
ся учет влияния СОЖ на тепловой баланс в зоне правки и температурное состояние
правящего инструмента для правки и круга.
По площади контакта алмаза со связкой
Т
ал
=
Т
с
;
q
а
=
q
с
, (65)
где
Т
с
−
температура связки, К;
q
а
и
q
с
−
соответственно поверхностная плотность теп-
лового потока в алмазе и связке, Вт/м
2
;
по площади контакта связки с корпусом

79
Т
с
=
Т
ко
;
q
с
=
q
ко
, (66)
где
q
ко
−
поверхностная плотность теплового потока корпуса алмазного карандаша или
алмаза в оправе, Вт/м
2
.
По наружной поверхности корпуса карандаша или алмаза в оправе, омываемой
СОЖ,
()
жко3ко
ко
ТТ
r
t
rr
−=
′
=
′
α
∂
∂
λ
, (67)
где
r
ко
−
радиус корпуса алмазного карандаша или алмаза в оправе, м (см. рис. 25);
α
3
−
коэффициент теплопередачи от СОЖ к корпусу (определяется расчетом или по лите-
ратурным данным), Вт / (м
2
⋅
К).
По наружной поверхности корпуса, не омываемой СОЖ,
()
в4ко
ко
ТТ
r
t
ко
rr
−=
′
=
′
α
∂
∂
λ
, (68)
где
α
4
−
коэффициент радиационно-конвективного теплообмена корпуса с окружаю-
щим воздухом (определяется по известным уравнениям подобия [117, 167] и с исполь-
зованием литературных данных [96, 130, 164, 167]), Вт/(м
2
⋅
К);
Т
в
−
температура окру-
жающего воздуха на рабочем торце корпуса (
у
=
∞
), К.
Приняв граничные условия (63)
−
(68), составим дифференциальное уравнение
теплопроводности круга. Первоначально примем, что у круга нет пор, заполненных
СОЖ и воздухом (сплошная модель круга), что соответствует, например, кругам на
металлической, бакелитовой и вулканической связках. Для дальнейших исследований
удобно воспользоваться цилиндрической системой координат (см. рис. 26).
В подвижной системе координат
r
,
ϕ
′
,
х′
(жестко связанной с кругом (см. рис.
26, в)):
′′
+
′′
⋅+⋅+
=⋅⋅
x
t
x
t
r
r
t
rr
t
r
t
с
∂
∂
λ
∂
∂
ϕ∂
∂
λ
ϕ∂
∂
∂
∂λ
∂
∂
λ
∂
∂
τ∂
∂
ρ
22
2
2
2кк
1
. (69)
В неподвижной системе координат
r
,
ϕ
,
х
, жестко связанной с правящим инстру-
ментом (см. рис. 26, б):
.
t
x
t
Sс
x
t
x
t
r
r
t
rr
t
r
t
с
к
+⋅⋅−
−
+
⋅+⋅+
=⋅⋅
ϕ∂
∂
ω
∂
∂
ρ
∂
∂
λ
∂
∂
ϕ∂
∂
λ
ϕ∂
∂
∂
∂λ
∂
∂
λ
∂
∂
τ∂
∂
ρ
прк
22
2
2
2кк
1
(70)
Учитывая, что высота круга, как правило, существенно меньше его диаметра
(для круглого наружного и плоского шлифования), а температура в различных точках
со временем изменяется незначительно [34, 36, 127], примем, что температурное поле
двухмерное
t
=
t
(
r
,
ϕ
), стационарное.
Тогда уравнение теплопроводности (70) примет вид:
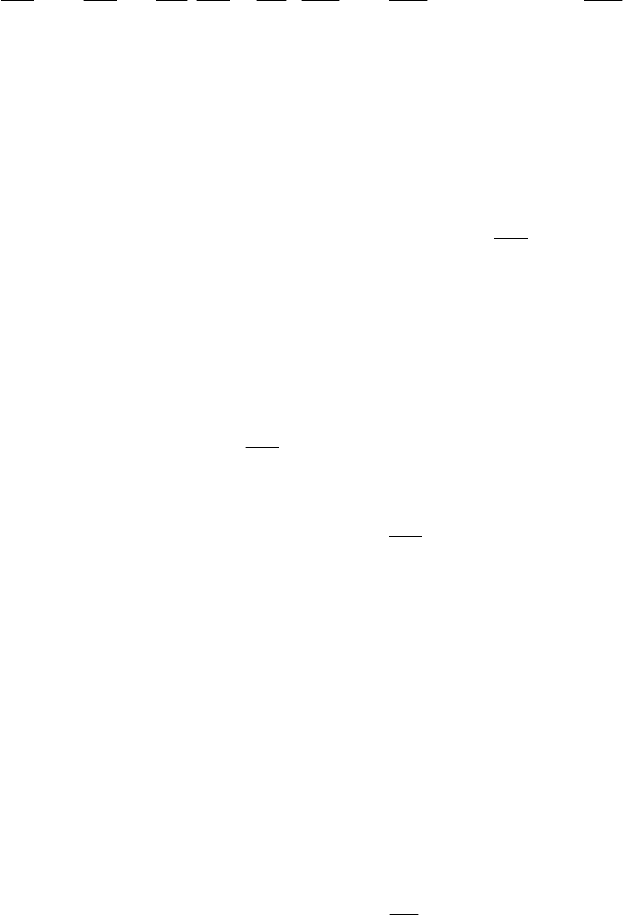
80
0
1
кк2
2
2
2
=⋅⋅⋅−
⋅+⋅+
ϕ∂
∂
ωρ
ϕ∂
∂
λ
ϕ∂
∂
∂
∂
λ
∂
∂
λ
∂
∂
t
с
t
r
r
t
rr
t
r
. (71)
Граничные условия:
1)
r
=
R
к:
:
−
ϕ
к
≤
ϕ
≤
ϕ
к
−
условия в виде (63), (64),
где
ϕ
к
−
угол, ограничивающий зону контакта круга с алмазным зерном, рад. (см. рис.
25);
2)
r
=
R
к
:
()
жкр52
ксож
сожк
к
ТТ
r
t
Rr
−=
−<≤
′′
−
′
≤<
=
α
∂
∂
λ
ϕϕϕ
ϕϕϕ
, (72)
где
α
5
−
коэффициент теплопередачи от СОЖ к кругу, Вт/(м
2
⋅
К);
ϕ′
сож
,
ϕ′′
сож
−
углы,
ограничивающие зону контакта круга с СОЖ, рад. (см. рис. 25)
3)
r
=
R
к
:
ϕ
′
сож
<
ϕ
< (2
π
−
ϕ
′′
сож
);
()
вкр42
к
ТТ
r
t
Rr
−=
=
α
∂
∂
λ
; (73)
4)
r
=
r
0
; 0 <
ϕ
< 2
π
; 0
=
r
t
∂
∂
. (74)
Получим теперь дифференциальное уравнение теплопроводности шлифовально-
го круга, поры которого заполнены СОЖ. Воспользуемся для этой цели неподвижной
цилиндрической системой координат в двумерном виде [
T
=
T
(
r,
ϕ
)] (см. рис. 26, б).
Учитывая, что изменения температуры в направлениях
r,
ϕ
и
Х
во времени незначи-
тельны [111, 118, 127], можно считать температурное поле стационарным.
Пористость круга
П
=
V
V
п
,
где
V
п
−
объем пор круга, м
3
;
V
−
полный объем круга, м
3
.
Теплопроводность пористого круга
λ
кп
=
λ
2
(1
−
П
) .
Уравнение теплового баланса для нашего случая (рис. 27) имеет вид:

81
dQ
ϕ
с
+
dQ
ϕ
ж
+
dQ
rc
+
dQ
rc
+
dQ
rж
+
dQ
ω
= 0 ; (75)
drd
q
dd
q
qqdQ ⋅⋅=
⋅+−=
ϕ
ϕ∂
∂
ϕ
ϕ∂
∂
ϕϕ
ϕϕϕ
rс
;
ϕ∂
λ
ε
ϕ
dt
r
q ⋅−=
к
;
drd
t
r
Q ⋅⋅
⋅=
ϕ
ϕ∂
∂
λ
ϕ∂
∂
∂
ϕ
εкc
1
; (76)
∂Q
ϕ
ж
=
G
ж
ϕ
⋅
С
ж
⋅
dt
; (77)
()
.ddr
r
q
rddr
r
q
ddrqdqdrq
ddrrdr
r
q
qdrqdQ
ϕ
∂
∂
ϕ
∂
∂
ϕϕϕ
ϕ
∂
∂
ϕ
⋅⋅−⋅⋅−⋅⋅−⋅−⋅⋅=
=⋅+⋅
⋅+−⋅⋅=
2
rr
rrr
r
rrrc
dtCGdQ ⋅⋅=
жrжжr
; (78)
dQ
ω
=
−
ω
⋅
r
⋅
dr
⋅
[
ρ
к
⋅
С
к
(1
−
П
) +
ρ
ж
⋅С
ж
⋅
П
]
dt
. (79)
После ряда преобразований
Рис. 27. Расчетная схема для вывода уравнения дви-
жения жидкости внутри круга:
V
r
,
V
ϕ
−
соответствен-
но радиальная и касательная скорости фильтрации

82
−
⋅+⋅⋅−
⋅+⋅+
ϕ∂
∂υ
∂
∂
υρ
ϕ∂
∂
λ
ϕ∂
∂
∂
∂λ
∂
∂
λ
∂
∂
ϕ
t
rr
t
с
t
rr
t
rr
t
r
ж
rжк
2
к
к
1
ε
ε
ε
()
[]
,
t
ПсПс
01
жжкк
=⋅⋅+−⋅⋅⋅−
ϕ∂
∂
ρρω
(80)
где
υ
r
и
υ
ϕ
−
скорости фильтрации СОЖ сквозь поры круга:
ϕρ
υ
dr
G
⋅⋅
=
ж
r
ж
r
;
dr
G
⋅
=
ж
ж
ρ
υ
ϕ
ϕ
, м/с;
G
жr
и
G
ж
ϕ
−
массовый расход СОЖ в радиальном и касательном на-
правлениях, кг/с;
λ
к
ε
−
эффективная теплопроводность пористого круга, Вт/(м
⋅
К);
λ
к
ε
=
λ
2
⋅
(1
−
П
) +
λ
ж
⋅
П
−
теплопроводность зоны круга с порами, пропитанными СОЖ;
λ
к
ε
=
λ
2
⋅
(1
−
П
) +
λ
в
⋅
П
−
теплопроводность зоны круга с порами, заполненными возду-
хом.
Таким образом, для дальнейших вычислений получены рабочие уравнения теп-
лопроводности (60)
−
(62) соответственно для кристалла алмаза, связки и корпуса ал-
мазного карандаша или алмаза в оправе, для круга сухого (без пор) и пропитанного
СОЖ.
2.1.2. Гидродинамика СОЖ при фильтрации сквозь поровое
пространство вращающегося шлифовального круга
Одним из путей проникновения СОЖ в контактные зоны при правке и шлифова-
нии является ее движение сквозь поровое пространство круга. Подача СОЖ сквозь по-
ры круга через центральное отверстие [169] или через клиновые полуоткрытые насад-
ки, расположенные у его торцев [50, 64, 67, 129], приводит к заполнению порового
пространства жидкостью. В результате замены воздуха СОЖ изменяются теплофизи-
ческие характеристики круга в целом и тепловой баланс процессов правки и шлифова-
ния.
Математическая модель движения СОЖ в контактную зону по порам круга при
подводе ее к его торцам была рассмотрена В.В.Ефимовым в работах [35
−
37]. Ему
удалось получить аналитическим путем и проверить экспериментально уравнение тра-
ектории движения СОЖ сквозь поры круга. Специфика попадания СОЖ в зону со-
вмещенного (торцекруглого) шлифования отражена в работах [61, 134, 157]. Исследо-
вания [35 – 37, 50, 61] позволяют однозначно утверждать, что, варьируя конструктив-
ными параметрами клинового полуоткрытого насадка и величиной начальной скоро-
сти пропитки кругов высотой до 120 мм, поровое пространство круга, примыкающее к
его периферии, можно всегда заполнить СОЖ.
83
Однако при рассмотрении фильтрации жидкости сквозь
поровое пространство круга в уравнениях [35 – 37, 72, 134] не учтены вязкостный
α
в
и
инерционный
β
и
коэффициенты гидравлического сопротивления [18], что недопустимо
при наличии динамической колебательной системы (вращающиеся шлифовальный
круг и заготовка, периодически перемещающийся или вращающийся правящий инст-
румент)
[
18
]
. Значения коэффициентов
α
в
и
β
и
в зависимости от условий шлифования
изменяются в широких пределах. Согласно работе [18]
α
в
=
а⋅
П
а
к
[ м
-2
] ; (81)
β
и
=
в
⋅
П
а
р
[м
-1
] , (82)
где
а
= (0,064
−
10,4)
⋅
10
4
;
в
= (1,15
−
72,0)
⋅
10
3
;
к
=
−
(4,4
−
5,0);
р
=
−
(5,6
−
5,9);
П
а
−
активная пористость круга:
П
а
=
V
пa
⋅
V
-1
,
где
V
пa
−
объем активных пор шлифовального круга.
Использовать значения
α
в
и
β
и
по рекомендациям [18] при расчете контактных
температур в зонах правки и шлифования с подачей СОЖ по внутренним трактам в
практических целях нельзя из-за низкой точности такого расчета [18, 99, 130, 166]. Да-
лее (см. параграф 2.4) будет показано, как можно определить величины
α
в
и
β
и
для ус-
ловий фильтрации СОЖ сквозь поры вращающегося шлифовального круга. Алгоритм
соответствующей программы для ПЭВМ приведен в работе [51].
Уравнения движения СОЖ [35 – 37, 72, 134], полученные без учета значений
вязкостного
α
в
и инерционного
β
и
коэффициентов гидравлического сопротивления
(т.е. с использованием закона Дарси для статических условий фильтрации жидкостей
сквозь неподвижные сыпучие тела), неправомерно использовать для расчетов расхода
СОЖ сквозь поровое пространство вращающегося круга из-за внесения существенных
ошибок в конечные результаты.
Опираясь на аналитические исследования В.В.Ефимова [35 – 37], попытаемся
получить уравнение движения жидкости по поровому пространству круга, свободное
от указанных недостатков, воспользовавшись схемой, показанной на рис. 27.
На выделенный элемент жидкости в пористом круге действуют внешние по-
верхностные силы или градиент давления, обусловленный избыточным давлением
СОЖ в зоне ее подвода (область
S
), центробежные или внутренние массовые силы, си-
лы сопротивления и капиллярный напор.
Учитывая, что скорость фильтрации мала по сравнению с окружной скоростью
шлифовального круга [72, 169], можно допустить, что подаваемый через неподвижный
насадок площадью S расход жидкости распределяется равномерно по площади
F
r
= 2
π
r
1
⋅H′
к
, где
Н′
к
−
единица высоты круга. В этом случае скорость фильтрации будет
определяться массовой плотностью тока
g
т
=
G
ж
/
F
r
на радиусе
r
1
, одинаковой по уг-
лу
ϕ
. Таким образом, процесс фильтрации в квазиустановившемся режиме можно счи-
тать осесимметричным (в подвижной системе координат), а касательную скорость
фильтрации можно принять равной нулю (
υ
ϕ
= 0).

84
Весь круг можно разделить на две
области: область
I
−
r
1
≤
r
≤
R
к
;
жидкость поступает через поверхность
F
длиной
L
1
= 2
π
⋅r
1
и шириной
Н′
к
и выходит
через поверхность
F
длиной
L
2
= 2
π
⋅R
к
и шириной
Н′
к
; область
II
−
r
0
<
r
<
r
1
;
поверхность
F
r
= 2
π⋅
r
0
⋅H′
к
непроницаема для жидкости, поэтому в области
II
после за-
полнения пор жидкостью устанавливается равновесие всех сил при радиальной скоро-
сти фильтрации
υ
r
= 0.
После заполнения СОЖ области
I
(при установившемся режиме) влиянием ка-
пиллярного напора можно пренебречь [36].
С учетом схематизации процесса и сделанных допущений для выделенного эле-
ментарного объема круга можно записать:
R
1
−
R
2
+
R
3
−
R
4
= 0, (83)
где
R
1
−
сила, действующая на площадку
АВ
, Н;
R
2
−
сила, действующая на площадку
СD
, Н;
R
3
−
центробежная сила, действующая на жидкость в объеме
ABCD
, Н;
R
4
−
си-
ла сопротивления движению в объеме
ABCD
, Н.
R
1
=
p
⋅
r
⋅
d
ϕ
, (84)
R
2
= (
p
+
dp
)
⋅
(
r
+
dr
)
⋅d
ϕ
=
p⋅r⋅d
ϕ
+
p⋅dr⋅d
ϕ
+
r
⋅
dp⋅d
ϕ
+
dp
⋅
dr⋅d
ϕ
.
Учитывая, что
dp⋅dr⋅d
ϕ
→
0,
R
2
=
p⋅r⋅d
ϕ
+
p⋅dr⋅d
ϕ
+
r⋅dp⋅d
ϕ
. (85)
Опуская промежуточные вычисления для
R
3
, можно записать
R
3
= 2
ρ
ж
⋅П⋅ω
2
⋅r
2
⋅dr⋅d
ϕ
. (86)
Из закона Дарси [21, 166, 176] и с учетом (81) и (82) следует, что
R
4
= (
α
в
⋅
µ
⋅
υ
r
+
β
и
⋅
υ
r
2
⋅
ρ
ж
)
⋅r⋅dr⋅d
ϕ
, (87)
где радиальная скорость фильтрации
υ
r
=
кж
ж
2
Hr
G
′
⋅⋅⋅
ρπ
, м/с . (88)
Подставив полученные соотношения (84)
−
(87) в (83), и разделив обе части
уравнения на
dϕ
, получим:
pr
−
pr
−
p
⋅
dr
−
r
⋅
dp
+ 2
⋅
ρ
ж
⋅П⋅
ω
2
⋅r
2
⋅dr
−
(
α
в
⋅
µ
⋅
υ
r
+
β
и
⋅
υ
r
2
⋅
ρ
ж
)
⋅
r⋅dr
= 0;
(89)2
4
2
2
22
ж
2
к
2
ж
2
2
кж
ж
22
жж
2
ив
.rП
нr
G
H
G
rПr)(
dr
)pr(d
жив
rr
⋅⋅⋅−
⋅⋅⋅
⋅
+
′
⋅⋅
⋅⋅
=
=⋅⋅⋅−⋅⋅+⋅⋅=−
ωρ
ρπ
β
ρπ
µα
ωρρυβυµα
Обозначив
2
к
2
ж
2
2
жи
ж
кж
жв
ж
4
2
Н
G
В;
Н
G
А
⋅⋅
⋅
=
⋅⋅
⋅⋅
=
ρπ
β
ρπ
µα
; (89, а)
С
ж
= 2
ρ
ж
⋅П
⋅ω
2
, получим уравнение движения СОЖ в следующем виде:
−d
(
p
⋅
r
) =
А
ж
dr
+
В
ж
d⋅
(
"n
r
)
−
С
ж
⋅r
2
⋅dr
. (90) Отсюда:
p
1
⋅r
1
−
p
2
⋅R
к
=
А
ж
(
R
к
−
r
1
) +
В
ж
⋅ln
R
к
⋅
(
r
1
)
-1
⋅
C
ж
⋅
3
-1
⋅
(
R
к
3
−
r
1
3
)
-1
. (91)
Для серединного сечения круга
