Кириллов И.И. Автоматическое регулирование паровых турбин и газотурбинных установок
Подождите немного. Документ загружается.


представляет собой случайный процесс, если заданы распределе-
ния вероятности коэффициентов
a
vh
, b
vh
для
любого момента вре-
мени. Метод исследования стохастических процессов открывает
возможность судить
об
усредненном поведении динамической
си-
стемы
под
влиянием ряда случайных воздействий, подчиненных
ре-
альным закономерностям.
Эргодическая гипотеза.
Во
многих случаях функции распре-
деления стационарного процесса могут быть определены
по
экс-
периментальным данным
для
одной
и той же
системы,
но за до-
статочно длительный промежуток времени.
При
этом результаты
наблюдений следует разделять
по
времени
на ряд
отрезков значи-
тельно большей длительности,
чем
условные периоды колебаний
переменных
в
данном процессе.
Базой
для
такого метода изучения процессов служит гипотеза:
обработка большого числа
п
наблюдений
за
стационарным случай-
ным процессом
в
одной
и той же
системе
и в
произвольно выбранные
моменты времени выявляет такие
же
статистические свойства,
какие имеют подобные системы
при том же
числе наблюдений
п,
но
в
один
и тот же
момент времени.
Корреляционная функция
R (t
u
t
2
). Так
называется математи-
ческое ожидание произведения величин случайной функции
в мо-
менты времени
t
t
и t
2
.
Аналогично тому,
как
уравнениями
А у =
к Ах
и
(21.17)
была установлена корреляция между двумя переменными,
для стационарного процесса
х (t)
корреляционная функция
на
отрезке времени
т = t
2
— t
x
может быть представлена
по
отноше-
нию
к
средней величине
т
х0
в
виде функции произведений мате-
матического ожидания
R
(т) = М [(х (0 — т
х0
) (х (t + x) — т
х0
) ]. (21.19)
В стационарных случайных процессах
со
свойством эргодич-
ности математическое ожидание равно средней величине
по
вре-
мени
для
интервала
27', и
можно корреляционную функцию
при
nixo
— 0
записать
так:
т
R(x) =
(2T)-
1
J
x{t)x{t
+ x)dt. (21.20)
—т
Таким образом корреляционная функция определяет вероят-
ность перехода функции
х (t),
имевшей
в
момент
t
величину
х
ъ
к величине
х
2
в
момент
t + т.
Этим характеризуется связь между
функциями
х (t) и х (t + т).
Математически свойство корреляции
выражает функция, получаемая
из (21.20)
путем расширения пре-
делов
до Т -»• оо.
Такая функция называется автокорреля-
ционной.
Функцию
R (т)
можно построить
по
точкам: помножить
ор-
динату
х (t) на х (t + т
х
) и
вычислить среднюю величину этого
произведения
в
интервале
2Т,
затем
те же
операции повторить
длят, равногот
2
,т
3
ит.
д.
Полученная таким образом функция
R (т)
всегда будет четной,
так как
изучается стационарный процесс.
420
В задачах
с
двумя связанными стационарными случайными
функциями
х (t) и у (0
помимо
их
корреляционных функций
R
x
(х) и R
y
(т)
вводится взаимная корреляционная
функция, которая
при т
х0
= т
и0
= 0
имеет
вид
т
R
xy
(x)
=
(l/2T)
J
x(t)y(t
+ i)dt. (21.21)
—г
Заменив
в (21.21)
интеграл суммой,
а
интервал времени
—
числом
измерений
N,
получим
R
= (1/Л0 t Ш- (21-22)
Величина
R
характеризует меру зависимости между двумя систе-
мами чисел
x
t
и y
t
, и она
выражает коэффициент кор-
реляции. Отметим нижеследующие особенности рассматри-
ваемой корреляционной функции
с
равным нулю средним значе-
нием
(т
х0
= 0).
Функция
х (t + т)
зависит
как от
параметров системы,
так
и
от
начального значения функции
х (t).
Если влияние последней
с возрастанием
т
ослабевает,
то при
больших
т
функция
х (t + х)
делается независимой
и
корреляционная связь исчезает,
т. е.
|
R (т) |
т-*со
= 0.
Начальное значение корреляционной функции
R (0)
при
т = 0 и
средней величине
т
х0
= 0
согласно
(21.19) и (21.20)
становится равным среднему значению квадрата случайной функ-
ции,
х. е. R (0) = х
2
.
Корреляционная функция
—
четная функция
от т, т. е. R (х) = R (—т), так как эта
функция
не меняется
от
смещения начала координат.
Спектральная плотность
S (со). Эта
функция представляет
со-
бой преобразование Фурье
от
корреляционной функции
R (т)
оо
оо
S
(со)
= \ R (т) е~
шх
dx = 2 J R (т) cos
сот
dx. (21.23)
—оо
0
Выражение корреляционной функции через
S (со)
запишем
аналогично
(5.2) и (5.3)
оо
R
(т) =
(2л)-
1
J S
(со)
е
ш
tico.
(21.24)
—оо
Уравнение
(21.24)
выявляет,
в
некоторой мере, порядок воз-
буждающих частот
в
исходных пульсациях. Таким образом уста-
навливается связь между корреляционной функцией
и
спектраль-
ной плотностью. Например, если корреляционная функция может
быть выражена экспонентой
R (т) =
е~Р
|т|
,
то
согласно
(21.23)
и табл.
5.1
получим
оо
оо
5
(со)
= 2 J R (т) cos
сот
cir = 2 j е-3 I
т
I
cos
сот
dx =
2р/(р
2
+ со
2
),
о
о
(21.25)
421

§
21.3.
ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА
СКВОЗЬ СИСТЕМУ РЕГУЛИРОВАНИЯ
Пусть полезный стационарный сигнал
т (t)
подан
к
входу
в
линейную динамическую систему
(рис.
21.5) и
известны
его корреляционная функция
R
m
(т)
и
спектральная плот-
ность
S
m
(со).
Поставим задачу найти корреляционную функ-
цию
R
x
(т)
и
спектральную плотность
S
x
(со)
при
выходе
из си-
стемы. Корреляционную функцию представим уравнением
(21.20),
выбрав
Т
достаточно большим, чтобы обеспечить высокую сте-
пень вероятности. Положим,
что
данная динамическая система
имеет импульсную переходную функцию
k (t),
получаемую
как
реакция
на
воздействие типа дельта-функции
(см.
§ 9.5).
Тогда,
рассматривая сигнал
m (t)
как
единичное воздействие,
на
выходе
из динамической системы получим функцию
x(t)= J m(t-X)k(X)dX, (21.26)
I—оо
где переменная
(t —
X)
охватывает
все
моменты времени,
в
которые прикладывались
к
системе воздействия типа дельта-
функции.
Точно
так
же
можно записать
x(t +
x)
= J m(t + т
—
r\)k(r))dr),
(21.27)
где
г)
имеет
тот
же
смысл
по
отношению
ко
времени
/ + т,
как X
по отношению
к t.
Подставив выражения
(21.26) и (21.27) в
уравнение
(21.20)
и заменив порядок интегрирования, найдем корреляционную
функцию
оо
оо
R
x
(r) = \ dX \
dy\k{r\)k(X)
(2Г)"
1
\ m (t + т -
п)m
(t -
X)
dt
—оо
—оо |_ —Т
(21.28)
Заменив
в
последнем интеграле, взятом
в
квадратные скобки,
переменную
t на t + X,
можем преобразовать
его
к
виду
г
(1/2Г)
f m (t + т +
Я,
-
Л)
/я(0 dt = R
m
(т
+
X
-
TJ),
m(t)
W(itx)]
Рис.
21.5.
Прохождение случайного сигнала m
(t)
x(tj
сквозь динамическую систему
с
частотной харак-
теристикой
W (t'to)
422
а значит
(21.28)
можно переписать
так:
оо
оо
R
x
(x)= J dX J k(X)k{r\)R
m
(x +
X-r\)dr\.
(21.29)
—оо
—оо
Последним уравнением определена связь между корреляцион-
ными функциями сигналов
m (t)
перед динамической системой
и
х
(t) за
нею.
Аналогичную зависимость можно установить
и
между
спектральными плотностями входного
и
выходного сигналов,
исходя
из
выражений
оо
S
x
(co)=
j
/?
ж
(т)е-'
и
Мт;
(21.30)
—оо
оо
S
m
(co)=
J
R
m
(x-\-X-r\)e-
ia
>
<'+*-ч>
dx. (21.31)
—оо
Опуская выкладки
[63],
приведем конечный результат
S
x
(w) = \W(m)\
2
S
m
((o), (21.32)
где
| W
(ш)
|
2
—
квадрат модуля передаточной функции динами-
ческой системы.
Таким образом, спектральная плотность
S
x
(со)
выходной
ве-
личины
из
динамической системы равна спектральной плот-
ности
S
m
(со)
входной величины, умноженной
на
квадрат модуля
передаточной функции динамической системы
W (too).
Применительно
к
турбинам знание спектральной плотности
для величины перемещения распределительных органов рабочего
тела имеет большое значение,
так как она
является одной
из ха-
рактеристик вынужденных колебаний лопаточного аппарата.
§
21.4.
ПРИМЕРЫ СТАЦИОНАРНЫХ СЛУЧАЙНЫХ
ПРОЦЕССОВ
В
СИСТЕМАХ РЕГУЛИРОВАНИЯ
Гидравлические
и
пневматические системы.
В
этих
системах нередко наблюдались резкие пульсации, вызванные
срывами потока
в
дроссельных органах. Такие колебания давле-
ния
в
импульсных линиях имели случайный характер, поскольку
срывные явления могли заметно меняться
в
зависимости
от
мно-
гих параметров
и
внешних импульсов
(от
наличия воздуха
в
жидкости,
от
вибрации,
от
положения дроссельных
и
отсечных
зо-
лотников
и
др.).
Вместе
с
тем случайный характер носили
и
колеба-
ния поршня сервомотора, подключенного
к
импульсным линиям.
Между пульсациями давления
в
местах срыва потока
и
коле-
баниями поршня сервомотора существует определенная связь,
которую характеризуют корреляционные функции.
На
рис.
21.6
представлен пример осциллограммы пульсаций
от-
сечного золотника
и
поршня сервомотора, наблюдавшихся
в
си-
стемах регулирования паровых турбин
(по
опытам
Л. И.
Черняв-
423
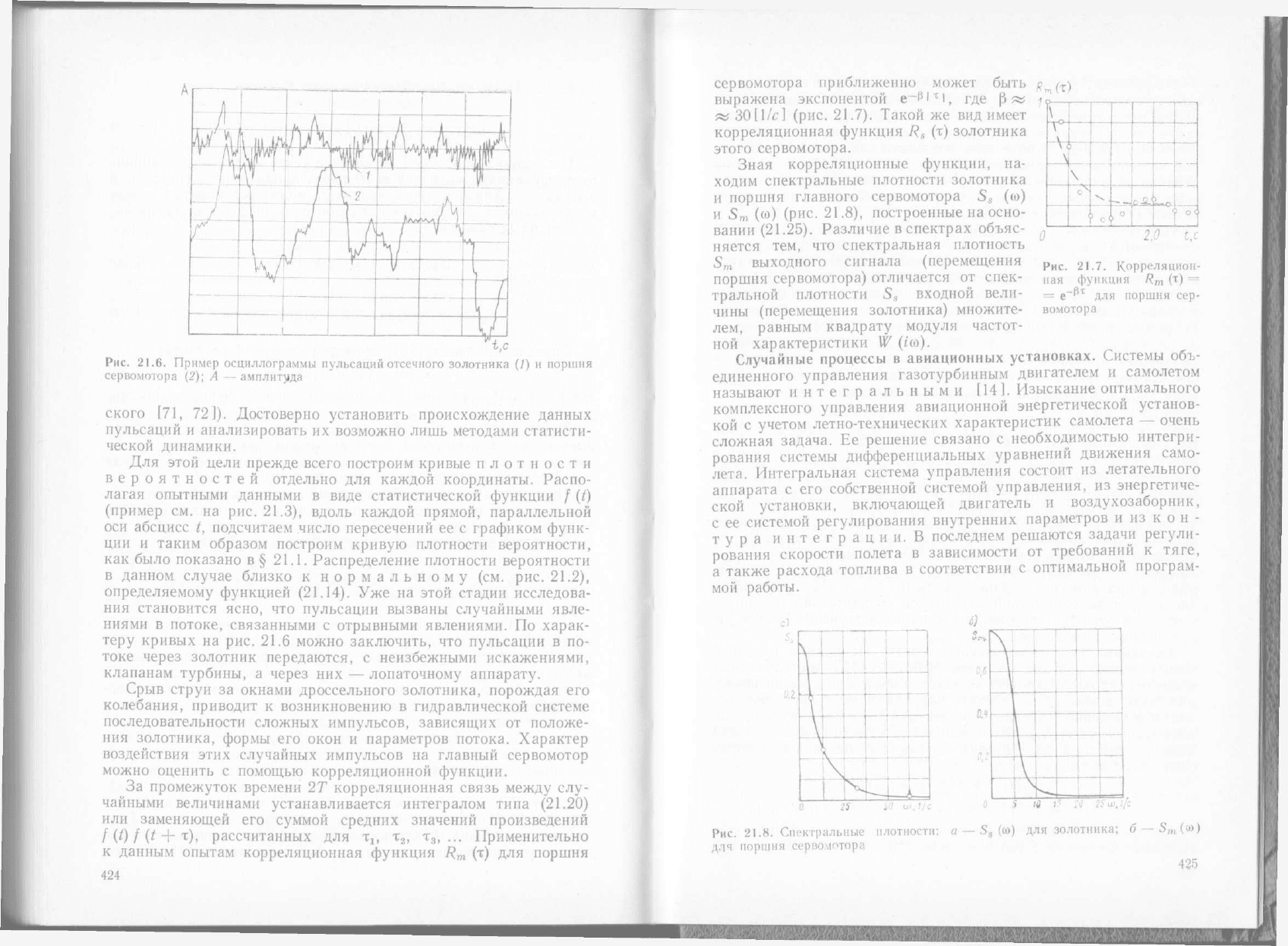
Рис.
21.6.
Пример осциллограммы пульсаций отсечного золотника
(/) и
поршня
сервомотора
(2); А —
амплитуда
ского
[71, 72]).
Достоверно установить происхождение данных
пульсаций
и
анализировать
их
возможно лишь методами статисти-
ческой динамики.
Для этой цели прежде всего построим кривые плотности
вероятностей отдельно
для
каждой координаты. Распо-
лагая опытными данными
в
виде статистической функции
/ (/)
(пример
см. на рис. 21.3),
вдоль каждой прямой, параллельной
оси абсцисс
t,
подсчитаем число пересечений
ее с
графиком функ-
ции
и
таким образом построим кривую плотности вероятности,
как было показано
в § 21.1.
Распределение плотности вероятности
в данном случае близко
к
нормальному
(см. рис. 21.2),
определяемому функцией
(21.14). Уже на
этой стадии исследова-
ния становится ясно,
что
пульсации вызваны случайными явле-
ниями
в
потоке, связанными
с
отрывными явлениями.
По
харак-
теру кривых
на рис. 21.6
можно заключить,
что
пульсации
в по-
токе через золотник передаются,
с
неизбежными искажениями,
клапанам турбины,
а
через
них —
лопаточному аппарату.
Срыв струи
за
окнами дроссельного золотника, порождая
его
колебания, приводит
к
возникновению
в
гидравлической системе
последовательности сложных импульсов, зависящих
от
положе-
ния золотника, формы
его
окон
и
параметров потока. Характер
воздействия этих случайных импульсов
на
главный сервомотор
можно оценить
с
помощью корреляционной функции.
За промежуток времени
2Т
корреляционная связь между слу-
чайными величинами устанавливается интегралом типа
(21.20)
или заменяющей
его
суммой средних значений произведений
/
(0 / (t + т),
рассчитанных
для т,, т
2
, т
3
, ...
Применительно
к данным опытам корреляционная функция
R
m
(т) для
поршня
424
\
V
\
\
V
\
\
•
n А
L.O.
1
>
с<
1
о
с
о
2,
с
Рис.
21.7.
Корреляцион-
ная функция
R
m
(т) =
= е~^
т
для
поршня сер-
вомотора
сервомотора приближенно может быть
выражена экспонентой
е Р'
т
I, где
р"
та
та
30
[
1/с] (рис. 21.7).
Такой
же вид
имеет
корреляционная функция
R
s
(т)
золотника
этого сервомотора.
Зная корреляционные функции,
на-
ходим спектральные плотности золотника
и поршня главного сервомотора
S
s
(со)
и
S
m
(со) (рис. 21.8),
построенные
на
осно-
вании
(21.25).
Различие
в
спектрах объяс-
няется
тем, что
спектральная плотность
S
m
выходного сигнала (перемещения
поршня сервомотора) отличается
от
спек-
тральной плотности
S,
s
входной вели-
чины (перемещения золотника) множите-
лем, равным квадрату модуля частот-
ной характеристики
W
(/со).
Случайные процессы
в
авиационных установках. Системы объ-
единенного управления газотурбинным двигателем
и
самолетом
называют интегральными
[14].
Изыскание оптимального
комплексного управления авиационной энергетической установ-
кой
с
учетом летно-технических характеристик самолета
—
очень
сложная задача.
Ее
решение связано
с
необходимостью интегри-
рования системы дифференциальных уравнений движения само-
лета. Интегральная система управления состоит
из
летательного
аппарата
с его
собственной системой управления,
из
энергетиче-
ской установки, включающей двигатель
и
воздухозаборник,
с
ее
системой регулирования внутренних параметров
и из к о н -
тура интеграции.
В
последнем решаются задачи регули-
рования скорости полета
в
зависимости
от
требований
к
тяге,
а также расхода топлива
в
соответствии
с
оптимальной програм-
мой работы.
Рис.
21.8.
Спектральные плотности:
а — S
s
(со) для
золотника;
б —
S
m
(a>)
д.дч поршня сервомотора

На рабочий процесс
в
энергетической установке
в
целом суще
ственное влияние оказывают случайные изменения внешних пара
метров неравномерного потока,
а
также таких величин,
как
дав
ление
и
температура воздуха перед двигателем, степень турбулент
ности воздуха
и др.
Кроме того, возможны сильные нестационар
ные явления
в
потоке внутри двигателя.
Эти
случайные сигналы
приходится учитывать
при
современных требованиях
к
быстро
действию
и
точности систем регулирования.
С
этой целью приме
няются статистические методы расчета.
При определении отклонений параметров элементов двигателя
принимается нормальный закон распределения. Нормальная
плотность вероятности определяется согласно
(21.14).
Нестацио
нарный режим рассматривается
для
различных значений отклоне
ний выходных параметров отдельных элементов
или
двигателя
в целом.
В
источнике
[14]
рекомендуются следующие режимы:
1)
режим наибольшей вероятности
Ax
t
= 0; его
вероятность
Ш
£
(0) =
Ютах
(A*l)a>max
(А*а) ••• ^тах
(&Х
п
);
2)
реЖИМ
С МЭК-
симальным значением отклонений параметров
Ax
t
= За, где о —
среднеквадратичное отклонение;
3)
режим
со
средними величи
нами
Ах
;
; 4)
специально статистически заданные режимы.
В воздухозаборнике пульсации давления состав
ляют
0,5—3 % от
величины
а.
Корреляционная функция имеет
вид экспоненты
R (т) = е
-
Р
1 т
I
при р
-1
= 0,5 :2 мс, а
спектраль
ная плотность
— вид (21.23). За
компрессором пульса
ции значительно меньше,
чем
перед
ним (0,3—0,6 %), а
корреля
ционная функция имеет гармоническую составляющую
R (т) =
__
е
—рIт|
cos
W()T) где
круговая частота со
0
/2я
= 25:50 Гц. 3 а
турбиной получается более широкий спектр; добавляются
частоты более высокие,
чем за
компрессором
(100—300 Гц); по
стоянная составляющая функции
5 (со) при
вибрационном горе
нии может повышаться
на
порядок; среднеквадратичное отклоне
ние температуры газа можно оценить
в 7—8 К [14].
Указанные
здесь примеры отклонений параметров сравнительно велики,
и
учет
их в
расчетах современных быстродействующих систем
ре
гулирования необходим.
Случайные колебания частоты
в
сети. Испытания натурной
электрической системы
по
схеме
МЭИ [15—17] при
случайных
возмущениях частоты
в
сети
на
входе
в
измеритель рассогласова
ния дали возможность оценить корреляционную функцию
R
m
для перемещений клапана турбины
и
взаимную корреля
ционную функцию
R
fm
для
изменений
как
частоты
в
сети,
так и
хода клапана турбины.
По
этим опытам была найдена аналитиче
ская аппроксимация
в
виде
R
f
(т)
= е
_
Р *
х
1
cos
сот
или
R
f
(
т
) = е-Р I
% 1
(cos
со
| т
]
+
(Р/со)
sin
со
| т |).
Эти корреляционные функции послужили
для
определения спек
тральной плотности
S (со) в
области существенных частот
в си
426
стемах регулирования. Кроме того,
в
итоге опытов была определена
также передаточная функция одной
из
моделей энергосистемы,
преобразующей «белый шум»
в
случайный процесс колебаний
частоты
в
сети.
Результаты исследования случайных процессов дают возмож
ность судить
о
связи между среднеквадратическими отклонениями
нагрузки
сх
м
и
частоты
ст
и
при
заданном коэффициенте нечувстви
тельности системы регулирования.
В зависимости
от
найденных показателей качества системы
ре
гулирования, функционирующей
при
случайных возмущениях
в сети, была вычислена относительная средняя длительность
пауз
t
между включениями релейного электрического сервомо
тора
с
учетом нечувствительности системы регулирования.
При
этом было установлено,
что
опасные
для
перегрева электрического
сервомотора частоты (более
0,4 Гц)
находятся
за
пределами суще
ственных частот, выявленных
на
основании анализа спектральной
плотности возмущений, поступающих
из
сети.
ЗАДАЧИ
И
ВОПРОСЫ
По проблемам теории автоматического регулирования
имеются сборники примерных расчетов
и
задач,
как
например
[31 ]. Они
относятся
в
основном
к
специальным разделам курса,
и
ими
следует пользоваться
во
время систематического изучения
каждой главы данного учебника. Здесь
же
приведены
как
при
меры вопросы
и
задачи
для
общего контроля освоения комплекса
знаний
по
теории автоматического регулирования турбин
в
целом.
Этот комплекс знаний связан
с
общей теорией паровых турбин
и
ГТУ
и с
проблемами повышения
их
надежности
и
экономичности.
Размышления
над
этими общими проблемами
и над
физическими
процессами, протекающими
во
всей динамической системе, зани
мают видное место
в
предлагаемых вопросах
и
задачах. Такая
их
ориентация полезна,
в
частности, применительно
к
письменным
экзаменам.
1.
Задачи автоматического регулирования
1.1.
Сформулировать задачи статики
и
динамики
ре
гулирования, управления
и
автоматизации турбинного агрегата.
Изобразить статическую характеристику регулирования
в
раз
личные моменты пуска турбины
и
синхронизации
и
разъяснить,
как проводится контроль
за
правильностью настройки системы
регулирования
с
помощью этой характеристики.
В
качестве при
мера исследовать
с ее
помощью последствия преждевременного
вступления
в
действие центробежного регулятора
при
наладке
регулирования
и
доказать,
что
такая ошибка может привести
к аварии.
Разъяснить термин саморегулирование агрегата
и дать примеры математических моделей объектов регулирования,
427

обладающих саморегулированием. Показать графически, как ме-
няются характеристики турбинного агрегата под влиянием авто-
матической системы регулирования частоты.
1.2. Сформулировать главные критерии качества переходных
процессов регулирования: перерегулирование, декремент колеба-
ний, период колебаний, автоколебания и др. и разъяснить их
физический смысл.
1.3. Разъяснить связь качества автоматического регулирова-
ния турбоагрегата с его надежностью и экономичностью. Обосно-
вать особую важность этой связи для турбинных установок на АЭС.
2. Регулятор. Задача Вышнеградского
2.1.
Чувствительный элемент современного регулятора
выполняется так, чтобы его можно было считать безынерционным
звеном. Разъяснить математическую модель такого элемента.
Сформулировать понятие об идеальном регуляторе. Разъ-
яснить характеристики неустойчивых регуляторов и их практи-
ческое применение.
2.2. Представить математическую модель регулятора прямого
действия с учетом приведенной массы к координате его положе-
ния г. Изложить метод определения приведенной массы для цен-
тробежного маятника и для регулятора давления поршневого типа.
Составить формулы для вычисления динамических констант ре-
гулятора. Разъяснить назначение катаракта в регуляторе. Сфор-
мулировать задачу Вышнеградского об устойчивости системы
автоматического регулирования, состоящей из регулятора с мас-
сой (колебательного звена) и объекта регулирования (интегри-
рующего звена). Изобразить диаграмму Вышнеградского.
2.3. Изложить принципы конструирования современного вы-
сокочувствительного и практически безынерционного регулятора,
состоящего из чувствительного элемента и усилителей. Доказать
возможность выполнения прямого цифрового регулятора.
3. Объект регулирования и исполнительный механизм
3.1.
Математическую модель ротора представить в виде
апериодического звена с динамической постоянной Т. Считать,
что момент инерции ротора задан. Вывести формулу для вычисле-
ния константы Т и исследовать изменение ее величины в зависи-
мости от режима работы одноступенчатой турбины при сопловом
регулировании. Указать, как влияют на величину Т перекрыши
клапанов.
3.2. Составить линеаризованное уравнение ротора конденса-
ционной турбины при условии, что она работает на электрическую
сеть параллельно с другими агрегатами и что ее регулировочный
клапан остается в заданном положении, а расход пара меняется
под влиянием скользящего давления р
х
перед клапаном и при по-
428
стоя иной температуре пара. Разъяснить, как должен действовать
регулятор частоты такой турбины при аварийном сбросе нагрузки
с генератора.
3.3. Разъяснить свойства саморегулирования парового турбо-
агрегата, работающего на изолированную электрическую сеть.
Для этого вывести уравнение ротора как апериодического звена
и найти математическое выражение его динамической постоянной,
а затем составить математическую модель системы регулирования,
состоящей из идеального регулятора, конденсационной турбины
(апериодического звена) и главного сервомотора без обратной связи
(интегрирующего звена). Аналогичную математическую модель
составить для турбоагрегата без свойств саморегулирования
(интегрирующее звено). Из сравнения показателей качества регу-
лирования обеих систем выявить эффект, вызванный саморегули-
рованием агрегата. Физическую сущность различия процессов
в сравниваемых системах пояснить на базе частотных характе-
ристик.
3.4. Составить и исследовать структурную схему и математи-
ческую модель системы регулирования одновальной ГТУ для при-
вода нагнетателя в предположении безынерционной камеры сго-
рания и пренебрежимо малом влиянии внутренних объемов
газа. Вывести уравнение движения ротора ГТУ (апериодического
звена) и найти выражение его динамической константы Т. Счи-
тать,
что топливный клапан перемещается посредством пневмати-
ческого сервомотора (апериодического звена). Установить, как
влияет динамическая постоянная ротора на показатели качества
всей динамической системы и какими техническими средствами
располагает конструктор для изменения константы Т при различ-
ных режимах работы ГТУ.
3.5. Исследовать математическую модель системы регулирова-
ния, состоящей из идеального регулятора, конденсационной тур-
бины с пренебрежимо слабыми свойствами саморегулирования
(интегрирующего звена) и главного сервомотора с обратной связью
(апериодического звена), перемещающего клапан. Определить
основные показатели качества всей системы регулирования. За-
тем устранить в сервомоторе этой системы обратную связь и про-
верить устойчивость образовавшейся второй системы по крите-
риям Гурвица. Сравнив динамические качества указанных двух
систем регулирования, сделать вывод о влиянии обратной связи
в сервомоторе на процесс регулирования.
3.6. Система регулирования состоит из идеального регуля-
тора, конденсационной турбины, модель которой — интегрирую-
щее звено с динамической постоянной Т
а
, и двух последовательно
включенных сервомоторов: промежуточного со време-
нем T
sl
и г л а в н о г о со временем T
s2
. Составить математиче-
ские модели и принципиальные схемы этой системы для трех слу-
чаев:
1) оба сервомотора имеют обратные связи (апериодические
звенья); 2) только главный сервомотор имеет обратную связь;
429

3) только промежуточный сервомотор имеет обратную связь.
Найти критерии устойчивости Гурвица для каждой системы и
на их базе сделать выводы о принципах проектирования как про-
межуточных, так и главных сервомоторов. Схема регулирования
показана на рис. 2.4.
Отметим для контроля хода решения задачи, что для первой
из данных систем один из критериев Гурвица имеет вид
Тц г Hz 6Т
а
> 0.
3.7. Составить математическую модель сервомотора с дроссель-
ным золотником. Определить, каким типовым звеном модели-
руется такой сервомотор Вывести формулу для определения
времени сервомотора. Разъяснить физическую сущность действия
обратной связи в сервомоторе с дроссельным золотником. Про-
вести аналогию действия этой обратной связи со свойствами само-
регулирования аккумулятора газа с дросселями рабочего тела
при входе его в емкость и выходе из нее.
3.8. Составить математические модели сервомоторов с отсеч-
ными и дроссельными золодниками. Сформулировать условия,
при которых их динамические качества можно считать равно-
ценными (без учета трения). Дать сравнительную оценку обоим
типам сервомоторов, характеризуя их чувствительность и расход
масла. Указать области их применения, сославшись на извест-
ные системы регулирования паровых турбин и ГТУ.
4. Корректирующие устройства
4.1.
Сформулировать назначение корректирующих уст-
ройств. Привести примеры их применения в системах автомати-
ческого регулирования турбин, работающих на электрические или
тепловые сети. Указать рациональные места расположения кор-
ректирующих устройств в структурных схемах автоматического
регулирования.
Составить структурную схему и дать математическое описание
введения сигналов по производной от регулируемой величины ко
входу в звено, моделирующее объект регулирования.
4.2. Составить математическую модель дифференциатора и
пояснить его роль как корректирующего устройства. С этой целью
рассмотреть структурную схему какой-либо системы автоматиче-
ского регулирования без дифференциатора, а затем — с дифферен-
циатором. Путем сравнения частотных характеристик этих двух
систем дать оценку изменения запаса по устойчивости в результате
введения дифференциатора.
Привести примеры выполнения дифференциаторов с использо-
ванием механических (например, маховика) или электрических
средств.
Отметить, в каких аварийных ситуациях в энергосистеме диф-
ференциатор необходимо блокировать.
430
4.3. Рассмотреть передаточную функцию разомкнутой цепи
последовательно включенных в равном количестве апериодиче-
ских и дифференцирующих звеньев и определить, при каких зна-
чениях динамических констант T
d
дифференцирующих звеньев
можно достигнуть с помощью этих звеньев теоретически полной
компенсации замедления в передаче сигналов сквозь апериодиче-
ские звенья с динамическими постоянными Т.
4.4. Сформулировать идею применения изодрома в ка-
честве корректирующего устройства в системах регулирования
турбин. Составить математическую модель изодромного регулиро-
вания частоты вращения турбины с установкой изодрома в обрат-
ную связь сервомотора. Доказать, что такое изодромное устрой-
ство частично создает эффект дифференциатора, включенного
в обратную связь.
Доказать, что изодром открывает возможность выполнять
устойчивыми системы автоматического регулирования с очень
малым и даже нулевым коэффициентом неравномерности регули-
рования частоты или давления.
Разъяснить, чем вызвано в системах с изодромом различие
между коэффициентами неравномерности регулирования и ре-
гулятора.
4.5. Сформулировать цель и форму применения регуля-
тора мощности в системах автоматического регулирова-
ния частоты в сети. Доказать положительное влияние регулятора
мощности на процесс регулирования частоты в сети. Оценить ре-
гулятор мощности как звено, служащее для оптимизации распре-
деления нагрузки между параллельно работающими турбогенера-
торами под управлением ЭВМ.
5.
Регулирование двух параметров
5.1.
Применительно к турбинам с отбором пара для
системы автоматического регулирования частоты вращения и
давления в камере отбора сформулировать статические
критерии автономности при различных режимах
работы и разъяснить их физический смысл. Для этого воспользо-
ваться диаграммой режимов, считая приближенно
прямыми линии постоянных расходов отбираемого пара G
0T
и давлений р
ог
. Рассмотреть качественные изменения статических
критериев автономности при работе турбины с сопловым регули-
рованием на режимах, соответствующих вступлению клапанов
в работу. Указать, как надо проектировать систему парораспреде-
ления, чтобы избежать крупных нарушений статических крите-
риев автономности.
5.2. При тех же условиях, как в задаче 5.1, составить мате-
матическую модель системы автоматического регулирования ча-
стоты в сети и давления в камерах отбора пара из турбины. Для
этого воспользоваться уравнениями ротора и емкости без учета
свойств саморегулирования этих объектов, т. е. в форме интег-
431

рирующих звеньев. Уравнения сервомоторов представить в виде
апериодических звеньев. Уравнения золотников записать, как для
обычного связанного регулирования. Оба регулятора считать
идеальными.
Из полученной системы линейных дифференциальных уравне-
ний найти критерии динамической автоном-
ности и разъяснить их физический смысл.
Приняв времена сервомоторов пренебрежимо малыми, сделать
переход к прямому регулированию и для этой упрощенной схемы
вновь рассмотреть критерии автономности.
6. Нелинейности в системах регулирования
6.1. В составе системы регулирования ссухим тре-
нием в чувствительном элементе безынерционного регуля-
тора имеются следующие звенья: турбина как интегрирующее
звено с динамической константой Т
а
и главный сервомотор как
апериодическое звено с временем T
s
. Рассмотреть математиче-
скую модель этой системы и изобразить процесс регулирования
при внезапном набросе полной нагрузки.
Указать признаки' нелинейности в этой задаче и найти соот-
ношение динамических констант, при котором возможны автоко-
лебания.
Разъяснить вредные последствия, которые могут повлечь
автоколебания во влажнопаровых турбинах.
6.2. Рассмотреть гидравлический сервомотор релей-
ного типа в системе регулирования, состоящей из идеаль-
ного регулятора и турбины, модель которой — интегрирующее
звено. Представить математическую модель всей системы регули-
рования, считая скорость поршня сервомотора постоянной по
величине, а изменения направления его движения мгновенными.
Разъяснить кинематическую схему релейного сервомотора на
примере условной рычажной передачи. Выяснить преимущества
релейного сервомотора по сравнению с обычным гидравлическим
сервомотором с отсечным золотником. Сравнение провести по
расходу масла и декременту колебаний.
Отметить, как выполняется электрический релейный серво-
мотор, аналогичный данному гидравлическому.
6.3. Рассмотреть метод расчета нелинейного процесса
регулирования при внезапном сбросе электрической нагрузки
с турбогенератора. Систему регулирования представить в составе
идеального регулятора, турбины как интегрирующего звена и
главного гидравлического сервомотора в качестве апериодиче-
ского звена. Применить метод Эйлера приближенного
численного интегрирования. Учесть нечувствительность системы
регулирования.
Указать несколько примеров нелинейностей, влияние которых
на процесс регулирования может быть исследовано данным ме-
тодом.
432
6.4. Указать признаки нелинейностей в системах регулирова-
ния и изложить методы линеаризации, включая обычную линеа-
ризацию и метод гармонической линеаризации нелинейностей.
Рассмотреть фильтрующее свойство интегрирующего
звена.
6.5. Показать на примере процесса регулирования с сухим
трением в чувствительном элементе регулятора, что некоторую
оценку влияния остановок муфты можно получить, введя соответ-
ствующее по времени звено запаздывания.
Разъяснить физический смысл критической частоты со
к
и кри-
тического запаздывания т
к
.
7. Защита турбины
7.1. Назвать основные защитные устройства паровой
турбины и ГТУ. Привести пример аварийной ситуации и протека-
ния процесса в электрической энергосистеме при утрате ее устой-
чивости.
7.2. Сформулировать главную задачу системы регулирования
в случае внезапного сброса с турбогенератора электрической
нагрузки.
Разъяснить, как можно использовать импульс по ускорению
с целью уменьшения максимального динамического заброса ча-
стоты вращения.
Объяснить роль регулятора безопасности в рассматриваемом
динамическом процессе. Привести характеристику регулятора
безопасности. Указать, в каком случае он должен действовать
и при какой частоте вращения стопорный клапан можно вновь при-
вести в рабочее состояние.
7.3. Разъяснить, как могут быть использованы ЭВМ в системе
защиты паровой турбины и ГТУ.

СПИСОК ЛИТЕРАТУРЫ
1.
Автоматизированная система управления турбины
К-800-240-5/А.
Ш.
Лейзерович,
А. Д.
Меламед,
В. А.
Панфи-
лов
и
др.//Электрические станции,
1984. № 6. С. 21—35.
2.
Айзерман
М. А.
Теория автоматического регулирования.
М.
Наука.
1966. 451 с.
3.
Андронов А.
А.,
Хайкин С.
Э.
Теория колебаний.
М.:
ОНТИ,
1937. 518
с.
4.
Биленко
В. А.,
Белькинд
Л. А.,
Исаева
3. И.
Особенности расчета
на
ЭВМ сложных систем регулирования энергоблоков//Теплоэнергетика.
1984.
№
8. С. 17—18. ,
5. Воронов А. А.
Теория автоматического управления.
В 2-х
частях.
М.:
Высш. школа,
ч. I. 1986. 367 с, ч. 2. 300 с.
6.
Веллер
В. Н.
Автоматическое регулирование паровых турбин.
М. :
Энер-
гия,
1977. 406 с.
7.
Вирченко М.
А.,
Жарницкая
Т. Я.,
Косяк Ю.
Ф.
Функция регулирова-
ния турбин АЭС//Теплоэнергетика.
1984. № 12. С. 19—22.
8.
Вознесенский
И. Н.
Жизнь, деятельность
и
избранные труды
в
области
гидромашиностроения
и
автоматического регулирования.
М.:
Машиностроение,
1962. 354 с.
9. Воронов А. А.
Основы теории автоматического управления.
В 2-х ча-
стях.
М.
Энергия,
1980. 309 с.
10.
Газотурбинные установки. Справочное пособие/Под
общ. ред.
Л.
В. А р с е н ь е в а и В. Г. Т ы р ы ш к и н а. Л.:
Машиностроение,
1978.
232 с.
11.
Иванов В. А.
Особенности регулирования турбоустановок АЭС//Тепло-
энергетика,
1982. № 4. С. 16—18.
12. Иванов В. А.
Регулирование энергоблоков.
Л.:
Машиностроение,
1982.
311 с.
13.
Иванов
В. А.,
Пахомов
В. А.,
Чернявский
Л. И.
Некоторые вопросы
повышения надежности
и
точности систем регулирования мощных турбин
с
про-
точными гидроусилителями//Теплоэнергетика.
1983. № 10. С. 38—41.
14.
Интегральные системы автоматического управления силовыми установ-
ками самолетов/Под
ред. А. А. Ш е в я к о в
а//М.: Машиностроение,
1983.
283 с.
15.
Калашников
А. А.
Динамика систем регулирования энергетических
турбин
при
случайных возмущениях//Теплоэнергетика.
1984. № 2. С. 39—41.
16.
Калашников
А. А.
Импульсные характеристики турбин
с
электрическим
приводом регулирующих клапанов//Труды
МЭИ. 1984. Вып. 623. С. 160—
164.
17.
Калашников
А. А.
Повышение эффективности систем регулирования
турбоустановок
с
электрическим приводом исполнительных органов. Автореф.
д.
т. н. М.:
МЭИ.
1986. 38 с.
18.
Кантор
С. А.
Регулирование судовых теплосиловых установок.
Л.:
Судпромгиз,
1956. 343 с.
19.
Кантор
С.
А.,
Кириллов
И. И. А. с. 108342.
СССР.
1957.
20.
Кетов
X. Ф.,
Кириллов
И. И.,
Пыж
О.
А. А. с. 339634.
СССР.
1934.
434
21.
Кириллов
И. И.
Автоматическое регулирование паровых
и
газовых
турбин.
М.:
Машгиз,
1961. 600 с.
22.
Кириллов
И. И.
Автоматические устройства паровых турбин.
Л.:
ОБТИ
1938. 195 с.
23.
Кириллов
И. И.
Влияние бойлера
на
динамическую устойчивость регу-
лирования паровых турбин.
Л.:
Труды
ЛПИ.
1938. С. 14—18.
24.
Кириллов
И. И.
Изменение амплитудно-фазовой характеристики
при
нарушении критериев динамической автономности//Теплоэнергетика.
1961. № 2
С.
14—17.
25.
Кириллов
И. И.
Исследование частотным методом динамики регулиро-
вания турбин
с
промежуточным перегревом пара//Изв. вузов. Энергетика.
1960.
№
10. С. 19—27.
26.
Кириллов
И. И.
Испытание элементов систем регулирования паровых
турбин. Труды ЦКТИ.
1947. Кн. 5. С. 5—31.
27.
Кириллов
И. И.
Нарушение критериев статической автономности
в си-
стемах регулирования нескольких величин//Теплоэнергетика.
1960. № 10
С.
17—20.
28.
Кириллов
И. И.
Регулирование паровых
и
газовых турбин.
Л.: ГЭИ,
1952. 427 с.
29.
Кириллов
И. И.
Регулирование турбин
с
отбором пара//Труды
НТС
по
теплотехнике.
1936. С. 44—76.
30.
Кириллов
И.
И.
Теория турбомашин.
Л.:
Машиностроение,
1972. 536 с.
31.
Кириллов
И.
И.,
Иванов
В. А.
Регулирование паровых
и
газовых тур-
бин.
Л.:
Машиностроение,
1966. 271 с.
32.
Кириллов
И. И.,
Иванов
В. А.,
Каленик
В. А.
Регулирование паро-
турбинных блоков
в
мощных энергосистемах//Энергомашиностроение.
1968
№
7. С. 27—31.
33.
Кириллов
И.
И.,
Иванов
В.
А.,
Мышкин
Н. С.
Автоматическое регули-
рование энергоблоков
при
скользящем начальном давлении пара//Энергомашино-
строение.
1976. № 1. С. 4—7.
34.
Кириллов
И. И.,
Иванов
В. А.,
Кириллов
А. И.
Паровые турбины
и
паротурбинные установки.
Л.:
Машиностроение,
1978. 276 с.
35.
Кириллов
И. И.,
Щербачев О.
В.,
Иванов
В. А.
Новые требования
к
па-
ротурбинным энергоблокам
для
покрытия пиков нагрузки
и
участия
в
аварий-
ном регулировании частоты
и
активной мощности//Электрические станции.
1972.
№
3. С. 18-22.
36.
Колобродов
Н. В.,
Кусакина
Л.
С,
Мельников
В.
С.
Микропроцессор-
ное устройство управления мощностью крупных паровых турбин/Микропро-
цессорные средства
и
системы.
1984. № 4. С. 65—68.
37.
Косяк
Ю. Ф.,
Вирченко
М. А.,
Рожанский
В.
Е.
Электрогидравли-
ческая система регулирования турбин АЭС//Теплоэнергетика.
1985. № 2.
С.
13—16.
38.
Кочуров
В. И.,
Тельнов
К. А.,
Рыбин
П.
А.
Доводка
и
испытание
си-
стем управления головного образца газоперекачивающего агрегата ГТН-25//Энер-
гомашиностроение.
1983. № 6. С. 2—5.
39.
Крамер Г.
Математические методы статистики.
М.: Мир, 1975. 648 с.
40.
Лернер А. Я.
Введение
в
теорию автоматического регулирования.
М.-
Машгиз,
1958. 352 с.
41.
Лейзерович
А. Ш.
Технологические основы автоматизации пусков
па-
ровых турбин.
М.:
Энергоиздат,
1983. 175 с.
42.
Лойцянский
Л. Г.,
Лурье
А. И.
Курс теоретической механики.
М.:
Наука,
т. 1. 1982. 352 с, т. 2. 1983. 640 с.
43.
Ляпунов А. М.
Общая задача
об
устойчивости движения.
М.:
Гостех-
издат,
1950. 386 с.
44.
Максвелл
Д. К.,
Вышнеградский
И. А.,
Стодола
А.
Теория автомати-
ческого регулирования/Под
ред. А. А.
Андронова
и И. Н.
Возне-
сен
с к о г о. М.: АН
СССР,
1949. 430 с.
45.
Малев
В.
В.,
Фрагин
М. С.
Автоматизация
—
основа повышения техни-
ческого уровня паровых турбин//Энергомашиностроение.
1986 № 3
С.
17—19.
435

46. Малев
В. В.,
Фрагин
М. С,
Мельников
В. С.
Развитие электрогндравли
ческих систем регулирования паровых турбин
ЛМЗ на
основе применения микро
процессорной технпки/УТеплоэнергетика.
1985. № 7. С. 12—16.
47. Михальцев
В. Е.,
Панков
О. М.,
Юношев
В. Д.
Регулирование
и
вспо
могательные системы газотурбинных
и
комбинированных установок.
М.:
Маши
ностроение,
1982. 255 с.
48. Ольховский
Г. Г.
Энергетические газотурбинные установки.
М.:
Энерго-
издат,
1985. 303 с.
49. Основы автоматического регулирования/Под
ред. В. В.
Солодов-
ни
к о в а. М.:
Машгиз,
т. 1. 1954—1959. 1117 с.
50. Панов
Е. И.
Электромеханическая система регулирования турбоагре-
гата. Автореф.
к. т. н. М.: МЭИ, 1986. 26 с.
51. Паротурбинные установки атомных электростанций/Под
ред. Ю. Ф. К о -
с
я к а, М.:
Энергия,
1978. 312 с.
52. Пивень
В. Д.,
Баясанов
Д. Б., Мед Г. А.
Автоматизация газотурбинных
установок.
Л.:
Машиностроение,
1967. 256 с.
53. Поляхов
Н. Н.,
Зегжда
С. А.,
Юшков
М. И.
Теоретическая механика.
Л.:
Изд. ЛГУ. 1985. 536 с.
54.
Попов
Е. П.,
Пальтов
И. Л.
Приближенные методы исследования нели-
нейных автоматических систем.
М.:
Физматгиз,
1960. 792 с.
55. Пчелкин
Ю. М.
Камеры сгорания газотурбинных двигателей.
М.:
Маши-
ностроение,
1984. 280 с.
56. Рабинович
А. В.,
Ивашов
В. Д.,
Иванов
С. Н.
Электрогидравлическая
система регулирования теплофикационной турбины//Электрические станции.
1975. № 11. С. 33—36.
57. Рабинович
А. В.,
Манькин
М. Н.,
Триголос
Г. С.
Система регулирования
паровой турбины Т-250/300-240//Теплоэнергетика.
1977. № 2. С. 6—13.
58. Ратнер
И. С.
Регулирование
и
режим работы газотурбинной установки
ГТ-100 ЛМЗ//Энергомашиностроение.
1984. № 1. С. 6—9.
59. Ратнер
И. С,
Боровков
А. И.,
Дядькин
Н. А.
Система управления тур-
биной ГТ-100//Энергомашиностроение,
1983. № 9. С. 17—20.
60. Романовский
П. И.
Ряды Фурье. Преобразование Лапласа.
М.:
Физмат-
гиз,
1959
.
303 с.
61. Рыжков
В. К.,
Пахомов
В. А.,
Фрагин
М. С.
Повышение надежности
и
качества систем регулирования мощных паровых турбин ЛМЗ//Теплоэнерге-
тика.
1981. № 1. С. 9—16.
62. Сафонов
Л. П.,
Селезнев
К. П.,
Коваленко
А. Н.
Тепловое состояние
высокотемпературных паровых турбин.
Л.:
Машиностроение,
1983. 295 с.
63. Солодовников
В. В.
Статическая динамика линейных систем автомати-
ческого управления.
М.: Изд. ФМ, 1960. 655 с.
64.
Тельнов
К. А.,
Файнштейн
А. А.,
Шабанов
С. 3.
Автоматизация газо-
перекачивающих агрегатов
с
газотурбинным приводом.
Л.:
Недра,
1983. 280 с.
65. Трояновский
Б. М.,
Филиппов
Г. А.,
Булкин
А. Е.
Паровые
и
газовые
турбины атомных электростанций.
М.:
Энергоиздат,
1985. 255 с.
66. Фрагин
М. С,
Щетинин
А. А.,
Волчегорский
М. Л.
Системы регулиро-
вания конденсационных турбин большой мощности ЛМЗ//Теплоэнергетика.
1972. № 11. С. 19—25.
67. Фрагин
М. С,
Помелов
С. Ю.,
Мельников
В. С.
Опыт освоения электро-
гидравлической системы регулирования К-800-240-5//Теплоэнергетика.
1986.
№
8. С. 13—16.
68. Фритч
В.
Применение микропроцессоров
в
системах управления.
М.:
Мир,
1984. 404 с.
69. Хутский
Г. И.
Приспособляющиеся системы автоматического управле-
ния
для
тепловых электрических станций. Минск: Наука
и
техника,
1968. 183 с.
70. Чарный
И. А.
Неустановившееся движение реальной жидкости
в
тру-
бах.
М.:
Недра,
1975. 295 с.
71. Чернявский
Л. И.
Повышение надежности
и
точности систем автомати-
ческого регулирования паровых
и
газовых турбин путем подавления пульсаций
в проточных гидросистемах.
Л.: ЛПИ.
Диссертация,
1986. 206 с.
72. Чернявский
Л. И.,
Абрамов
В. В.,
Аршаница
В. П.
Освоение электро-
436
гидравлической системы регулирования
и
защиты
ГТУ
ГТ-100//Энергомашино-
строение.
1983. № 9. С. 21—23.
73. Швец
И. Т.,
Федоров
В. И.
Динамика тепловых процессов стационарных
газотурбинных установок. Киев: Наукова думка,
1972. 279 с.
74.
Щегляев
А. В.,
Смельницкий
С. Г.
Регулирование паровых турбин.
М.:
Госэнергоиздат,
1962. 256 с.
75. Юревич
Е. И.
Теория автоматического управления.
Л.:
Энергия,
1975.
413 с.
76.
Besch
P., Ludwig Н., Loftier С. Gegenwartige Stand und weitere
Entwick-
lung
der Kraftwerksautomatisiening in der DDR//Energietechnik. 1982. H. 4.
S. 113—118.
77.
Follinger
O. Nichtlineare Regelungen//Berlin.
Akad.
Verl.
1980. 227 S.
78.
Follinger
O. Regelungstechnik.
Berlin.
AEG. 1980. 414 s.
79.
Teichmann
W. Angewandte Anlagenautomatisierung. VEB
Verl.
Techn.
Berlin.
1983. 268 s.
80.
Wenzel
J. Die Bedeutung der
Mikroelektronik
fur die Prozepuberwachung
im Kraftwerk//Kraftwerksanlagenbau. 1984. N 1. S. 41—45.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоколебания 214, 225, 233
Автомат безопасности 67, 73, 298, 379
гидродинамический 298
Автоматизация 9
Автономность системы регулирования
351
динамическая 358
— статическая 366, 409
Алгоритмы 400, 401 i
Амплитуда резонансная 111
АФХ 100
Блок котел—турбина 302
— предварительной защиты 71
Блочная схема ЭЧСР-М 403
Быстродействие системы 255, 389, 397
Величины малые 82
— случайные 411
Влияние масс 161
Воздействие внешнее 143
— возмущающее 8, 122
— единичное ступенчатое 204
— управляющее 8, 101, 120
в многосвязных системах 407
Время емкости 150
— катаракта 155, 158
— относительное 175
— переходного процесса 130, 133
— регулятора 155
— ротора 148
— сервомотора 162
Выключатель 179
— гидравлический 28
— сервомотора 25
— силовой 26, 295
Газогенератор 289
Газопровод магистральный 388
Гипотеза эргодическая 420
Горелка запальная 295
— рабочая 295
ГТУ без газового объема 287
— второго рода 273
— двухвальная 274, 289, 291
— одновальная 287
—, остановка 301
— первого рода 273
— постоянного горения 272
—, пуск 299
—, уравнение ротора 275
Датчик 343
— давления 343
— мощности 343
Движение асимптотически устойчивое
130
— неустойчивое 88
— установившееся 6, 7
— устойчивое 88
Декада 114
Декремент колебаний 8, 133
логарифмический 133, 158, 177.
180, 331
Дельта-функция 137
Диаграмма Вышнеградского 181
— режимов турбины 352
Дисперсия 416
Дифференциатор 113, 187, 188
Д-разбиение 103, 104
Дросселирование двойное 32, 171, 265,
376
Дроссель 30
—, расчет 30
Емкость между турбиной и компрессо-
ром 277
— переменная 151
— постоянная 149
— с внешним теплообменом 282
Заброс динамический 176, 179, 330
Задача Вышнеградского 181
Задвижка парозапорная 72
Зажигание 295
Запаздывание 239, 283
— критическое 240
Запас устойчивости 128, 129
Заслонки промежуточного перегрева-
теля 378
438
Защита 70
— беззолотниковая 73
— от повышения температуры 299
— предварительная 71
— противоаварийная 389
— противопомпажная 298
— турбин АЭС 372
Защитные устройства 73
• беззолотниковые 73
Звено апериодическое 108, 116, 143,
159, 217, 231, 286
— безынерционное 108, 117
— дифференцирующее 108, 186
— запаздывания 239
— интегрирующее 112, 115
— колебательное 108, 231
— следящее 33
— эквивалентное 124
АФХ 322, 324
Звенья инвариатные 139
— простые 107
Золотник 24
— двойного дросселирования 31, 32,
171, 265, 269
— дроссельный 33
— отсечный 24, 29
Золотник—пластина 34
Изображение Лапласа 78
Изодром 63, 192
Импеллер 368
Импульс по производной 344
Интеграл Фурье 77
Интегрирование численное 332
И-регулятор 202
Исчисление операционное 76
Камера сгорания 283, 285, 291
Катаракт 153, 155
Клапан выпускной 298
— дежурного горения 295
— обратный 72, 386
— отсечный 70
— регулировочный 7, 44
— сбросной 70
— стопорный 67
Клапаны 44, 303
Колебания вынужденные 85, 87
— гармонические 91, 137, 138
— малые 143
— свободные 85
— случайные частоты в сети 426
Кольцо регулировочное поворотное 44
Конденсат в теплообменных аппара-
тах 385
Константа динамическая 141, 143, 145,
157, 162, 210, 338
ротора 307
— —, экспериментальное определение
109
Контур минимального давления 394
— управления быстродействующий 389
— •— медленнодействующий 399
Конус дроссельный 306
Координата входная 85
— выходная 85
Коррекция степени неравномерности
60, 344
Корреляция 419
Коэффициент неравномерности 17
местный 60, 61, 210, 341
— — регулирования 17, 42
— нечувствительности 19, 391
— обратной связи 401
— расхода 44
—• саморегулирования 150
— усиления 150, 210, 220
Критерии автоколебаний 260
— автономности динамические 355, 358
статические 354, 368
— апериодичности 131
— монотонности 132
— устойчивости 194
Гурвица 93, 326
• Михайлова 95
Найквиста 99
Рауса 93, 326
Критерий автономности 351, 359
, нарушения 359
Линеаризация 210, 219, 227
— гармоническая 209
нелинейностей 209, 218
— обычная 208
Линии защиты предельные 298
Лопатки направляющие поворотные
45, 278
Люфты в шарнирах 214
Маневренность установки 373
Масса приведенная 154, 159
Маятник центробежный 153
Метод малых колебаний 76
— расчета на сброс нагрузки 331
— частотный 9
— численного интегирования 332
МУТ 47
— в непрямом регулировании 50
— в прямом регулировании 49
МикроЭВМ 399, 403
М-критерий 136
Множитель неавтономности 365
Модель математическая 9, 76, 128,
161, 169, 205, 315
третьего порядка 180
— линейная 84
Момент движущих сил 142
— сопротивления 142
электрического генератора 144,
277
