King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

3.4 Discrete probability distributions

A widely used technique to display sample data graphically is to prepare a histogram

(etymological roots – Greek: histos – web, or something spun together; gram –

drawing). A histogram is a frequency distribution plot containing a series of rec-

tangles or bars with widths equal to the class intervals and with heights equal to the

frequency of observations for that interval. The area of each bar is proportional to

the observed frequency for the class interval or range that it represents. A histogram

provides a pictorial view of the distribution of frequencies with which a certain

characteristic is observed in a population. Four histograms are plotted in Figure 3.1

(see Box 3.1). The observed variable in these histograms, which is plotted along the

x-axis, is the moderate to vigorous physical activity of children per weekday.

The observed variable in Figure 3.1 is a continuous variable. The durati on of

physical activity measured in minutes can take on any value including fractional

numbers. Continuous variables can be contrasted with discrete variables that take on

discontinuous values. For example, the number of cars in a parking lot on any given

day can only be whole numbers. The number of kitten s in a litter cannot take on

fractional or negative values. A measured or observed variable in any experiment for

which we can produce a frequency distribution or probability distribution plot is

called a random variable. A random variable is a measurement whose value depends

on the outcome of an experiment. A probability distribution plot speciﬁes the

probability of occurrence of all possible values of the random variable.

Using MATLAB

The function hist in MATLAB generates a histogram from the supplied data – a

vector x containing all the experimentally obtained values. MATLAB automatically

determines the bin (class interval) size and number of bins (default n = 10) for the

plot. The syntax for the hist function is

hist(x) or hist(x, n)

where n is the user-speciﬁed number of bins.

Another syntax is

[f, y] = hist(x, n)

where f is a vector containing the frequency for each bin, and y is a returned vector

containing the bin centers. One may also manually specify bin locations by feeding a

vector of values as an input argument.

The bar function in MATLAB draws a bar graph. The bar function plots the

random variable vector x along the x-axis and draws bars at each x value with a

height that corresponds to their frequency of observations, stored in variable y. The

syntax for the bar function is

bar(x, y)

where x and y are both vectors.

The frequency of observations of a population variable is an indicator of the

probability of its occurrence within the population. One can easily compute these

probabilities by determining the relative frequency of each observation. For

157

3.4 Discrete probability distributions

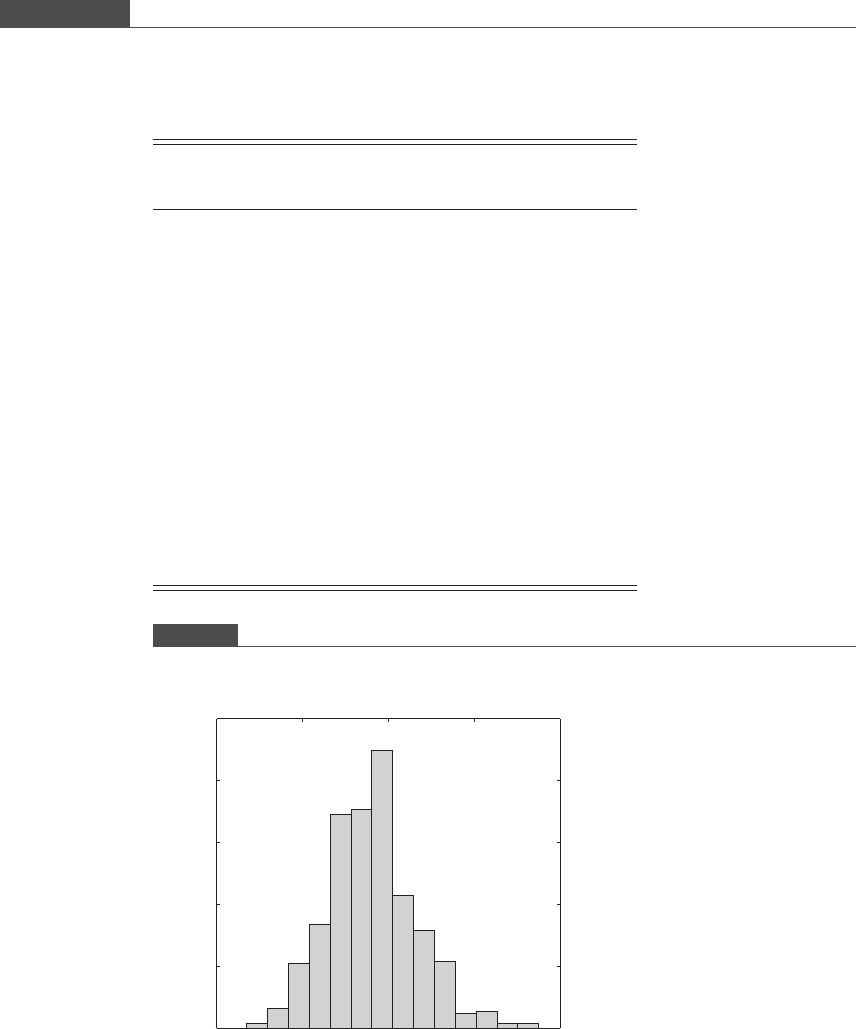
example, the histogram (age 9) in Figure 3.1(a) is replotted in Figure 3.3. The relative

frequency distribution is obtained by dividing all frequency bars by n = 839. We

now have a probability dist ribution of the duration of physical activity that children

of age 9 in the USA engaged in during the time period 1991 to 2007. In order to

generate this plot, [f, y] = hist(x, n) was ﬁrst used to determine f and y. The

relative frequency distribution was plotted using the bar function after dividing f

Figure 3.3

Relative frequency distribution or probability distribution of the duration of moderate to vigorous physical activity per

weekday for children of age 9 in the USA (Nader et al., 2008).

0 100 200 300 400

0.05

0.1

0.15

0.2

0.25

Moderate to vigorous physical activity

per weekday (minutes)

Relative frequency or probability

Table 3.4. Tabulated probability distribution of the duration

of moderate to vigorous physical activity per weekday for

children of age 9 in the USA (Nader et al., 2008)

x: moderate to vigorous physical activity for

age 9 children (minutes) P(x)

35.0–59.3 0.0036

59.3–83.6 0.0155

83.6–107.9 0.0524

107.9–132.1 0.0834

132.1–156.4 0.1728

156.4–180.7 0.1764

180.7–205.0 0.2241

205.0–229.3 0.1073

229.3–253.6 0.0787

253.6–277.9 0.0536

277.9–302.1 0.0119

302.1–326.4 0.0131

326.4–350.7 0.0036

350.7–375.0 0.0036

158

Probability and statistics

by 839 (i.e. bar(y, f/839)). The information provided in Figure 3.3 is also

conveyed in Table 3.4. Note that the assumption of random sampling, perfect

heterogeneity of the sample, and no bias in the sampling is implicit when a relative

frequency diagram is used to approximate a probability distribution. To calculate

the probability or relative frequency of occurrence of the population variable

within one or more intervals, determine the fraction of the histogram’s total area

that lies between the subset of values that deﬁne the interval(s). This method is

very useful when the population variable is continuous and the probability dis-

tribution is approximated by a smooth curve.

The shape of the histogram conveys the nature of the distribution of the observed

variable within the sample. For example, in Figure 3.1 the histogram for age 9

children has a single peak, and the distribution falls off symmetrically about the

peak in either direction. The three histograms for ages 11, 12, and 15 are progres-

sively skewed to the right and do not show a symmetrical distribution about the

peak. What does this tell us? If we are randomly to choose one child from the age 9

population, there is a greater probability that his/her mod erate to vigorous activity

level will be close to the peak value. Also, it is with equal probability that we would

ﬁnd a child wi th greater activity levels or with lower activity levels than the peak

value. These expectations do not hold for the 11-, 12-, and 15-year-old population

based on the trends shown in the histograms plotted in Figure 3.1. In a skewed

distribution, the peak value is usually not equal to the mean value.

3.4.1 Binomial distribution

Some experiments have only two mutually exclusive outcomes, often deﬁned as

“success” or “failure,” such as, live or dead, male or female, child or adult, HIV+

or HIV−. The outcome that is of interest to us is deﬁned as a “successful event.” For

example, if we randomly ch oose a person from a population to ascertain if the

person is exposed to secondhand smoke on a daily basis, then we can classify two

outcomes: either the person selected from the population is routinely exposed to

secondhand smoke, or the person is not routinely exposed to secondhand smoke. If

the selection process yields an individual who is exposed to secondhand smoke daily,

then the event is termed as a success. If three people are selected from a population,

and all are routinely exposed to secondhand smoke, then this amounts to three

“successes” obtained in a row.

An experiment that produces only two mutually exclusive and exhaustive

outcomes is called a Bernoulli trial, named after Jacques (James) Bernoulli

(1654–1705), a Swiss mathe matician who made signiﬁcant contributions to the

development of the binomial distribution. For example, a coin toss can only

result in heads or tails. For an unbiased coin and a fair ﬂip, the chance of

getting a head or a tail is 50 : 50 or equally likely. If obtaining a he ad is deﬁned

as the “successful event,” then the probability of success on ﬂipping a coin is 0.5.

If several identical Bernoulli trials are performed in succession, and each

Bernoulli trial is independent of the other, then the experiment is called a

Bernoulli process.

A Bernoulli process is deﬁned by the following three characteristic s:

(1) each trial yields only two events, which are mutually exclusive;

(2) each trial is independent;

(3) the probability of success is the same in each trial.

159

3.4 Discrete probability distributions

Example 3.6

Out of a large population of children from which we make five selections, the proportion of boys to girls in

the population is 50 : 50. We wish to determine the probability of choosing exactly three girls and two boys

when five individual selections are made. Once a selection is made, any child that is selected is not

returned back to the population. Since the population is large, removing several individuals from the

population does not change the proportion of boys to girls.

The probability of selecting a girl is 0.5. The probability of selecting a boy is also 0.5. Each selection

event is independent from the previous selection event. The probability of selecting exactly three girls

and two boys with the arrangement GGGBB is 0.5

× 0.5

= 0.5

= 1/2

. The probability of selecting

exactly three girls and two boys with the arrangement GBBGG is also 0.5

× 0.5

= 0.5

= 1/2

. In fact,

the total number of arrangements that can be made with three girls and two boys is

3! 5  3ðÞ!

¼ 10:

An easy way to visualize the selection process is to consider five empty boxes: □□□□□. We want

to mark exactly three of them with “G.” Once three boxes each have been marked with a “G,” the remaining

boxes will be marked with a “B.” The total number of combinations that exists for choosing any three of

the five boxes and marking with “G” is equal to C

. Thus, we are concerned with the arrangement of

the “G”s with respect to the five boxes. The total number of arrangements in which we can mark three

out of five boxes with “G” is equal to the total number of combinations available to choose three girls and

two boys when five selections are made. The order in which the three girls are selected is irrelevant.

The probability of selecting exactly three girls and two boys is given by

number of combinations possible  P girlðÞP girlðÞP girlðÞP boyðÞP boyðÞ¼

Thus, the probability of choosing exactly three girls in five children selected from a population where

the probability of choosing a girl or a boy is equally likely is

What if our population of interest has a girl to boy ratio of 70 : 30? Since the proportion of girls is

now greater to that of boys in the population, it is more likely for the selection group of five children to

contain more girls than boys. Therefore selecting five boys in succession is less probable than selecting

five girls in succession. Since every selection event is a Bernoulli trial and is independent of every other

selection event, the probability of selecting exactly three girls in five selection attempts from the population

is equal to C

ð0:7Þ

ð0:3Þ

Whatistheprobabilityofselectingfourgirlsandoneboy,ortwogirlsandthreeboys,oronegirl

and four boys? If the selection of a girl is termed as a success, then the probability of obtaining 0, 1, 2, 3,

4, or 5 successes in a Bernoulli process that consists of five Bernoulli trials is given by the binomial

distribution.

If a Bernoulli trial is repeated n times, and each Bernoulli trial is independent of the other, then the

probability of achieving k out of n successes, where 0 k ≤ n, is given by the binomial distribution.If

p is the probability of success in a single trial, then the probability (or relative frequency) of k successes

in n independent trials is given by

PksuccessesðÞ¼C

ð1  pÞ

nk

: (3:12)

A binomial distribution is an idealized probability distribution characterized by only

two parameters, n – the number of independent trials and p – the probability of

success in a single Bernou lli trial. Many experiments in manufacturing, biology, and

public healt h studies have outcomes that closely follow the binomial dist ribution.

160

Probability and statistics

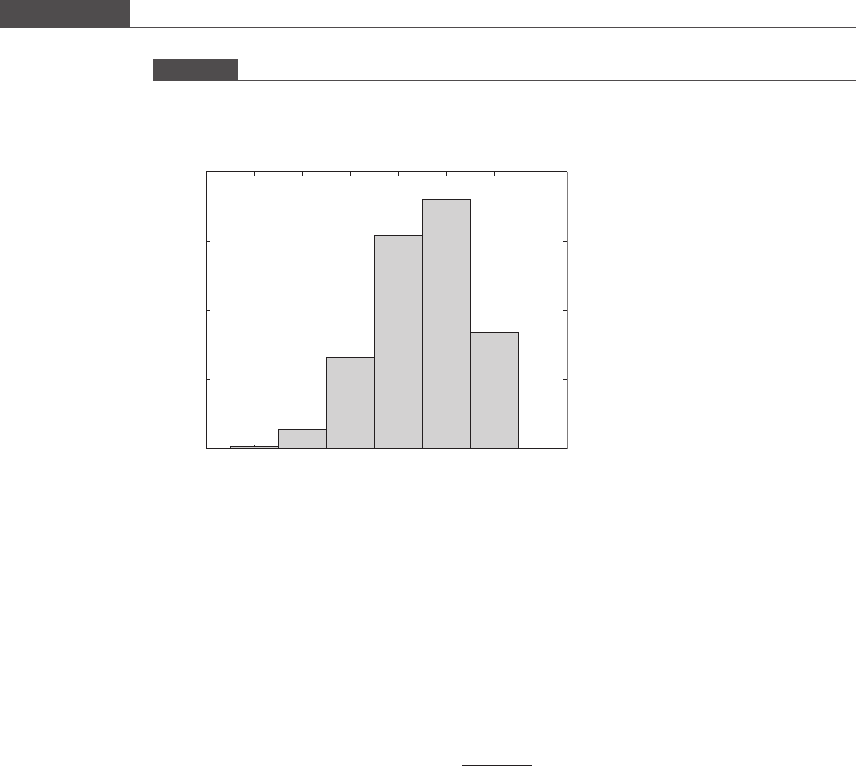
Using the formula given by Equat ion (3.12), we can generate a binomial distribution

for Example 3.6.Ifn = 5 and p = 0.7, Figure 3.4 is a plot of the binomial distribu-

tion that characterizes the probabilities of all possible outcomes of the experiment.

There are six possible outcomes of a Bernoulli experiment consisting of ﬁve

independent trials: 0, 1, 2, 3, 4, and 5 successes.

If p is the probability of success in a Bernoulli process, and q is the probability of

failure, then the sum of the probabilities of all outcomes in a bin omial distribution is

given by

k¼0

nk

¼ q

þ npq

n1

nðn  1Þ

n2

þþnp

n1

q þ p

¼ðp þ qÞ

In other words, the sum of the binomial distribution probabilities is equal to the

binomial expansion of ðp þ qÞ

. Since q =1–p,

k¼0

nk

¼ 1

¼ 1: (3:13)

A binomial distribution is strictly valid when sampling from a population is done

with replacement since this ensures that the probability p of success or failure does

not change with each trial when the population is ﬁnite. When sampling is performed

without replacement, which is usually the case, the binomial distribution is still

applicable if the population size N is large compared to the sample size n (or, n 

N) such that p changes minimally throughout the sampling process.

The “measured variable” or random variable in a binomial experiment is the

number of successes x achieved, and is called a binomial variable. Let’s calculate the

mean value and the variance of the binomial probability distribution of the number of

successes x. The mean value is the number of successes, on average, that one would

expect if the Bernoulli experiment were repeated many, many times. The mean and

variance serve as numerical descriptive parameters of a probability distribution.

Figure 3.4

Binomial distribution in which the event of selecting a girl from a given population of children has probability p = 0.7

and is denoted as a “success.” Five independent trials are performed in succession.

0 1 2 3 4 5

0.1

0.2

0.3

0.4

Number of successes (

irls)

Probability

Binomial distribution (n = 5; p = 0.7)

161

3.4 Discrete probability distributions

For any discrete probability distribution P(x), the expected value or expectation of the measured

variable x is equal to the mean μ of the distribution and is defined as

ExðÞ¼μ ¼

xP xðÞ: (3:14)

The mean is a weighted average of the different values that the random variable x can assume, weighted

by their probabilities of occurrence.

The expected value for the number of successes x in any binomial experiment

consisting of n Bernoulli trials is calculated as follows:

ExðÞ¼

xP x successesðÞ¼

x¼0

nx

x¼0

x! n  xðÞ!

nx

x¼1

ðx  1Þ! n  xðÞ!

nx

¼ np

x¼1

ðn  1Þ!

ðx  1Þ! n  xðÞ!

x1

nx

¼ np

x¼1

n1

x1

nx

;

where

x¼n

x¼1

n1

x1

nx

is the binomial probability distribution for n – 1 inde-

pendent trials (substitute y = x – 1 to verify this).

From Equat ion (3.13),

ExðÞ¼μ ¼ np  1 ¼ np: (3 :15)

For a binomial distribution, the average number of successes is equal to np.

Variance was deﬁned in Section 3.2 as the average of the squared de viations of the

data points from the mean value μ of the data set. The variance of the random

variable x that follows a discrete prob ability distribution P(x) is equal to the expect-

ation of x  μðÞ

For any discrete probability distribution P(x), the variance of x is defined as

¼ Eð x  μðÞ

Þ¼

x  μðÞ

PxðÞ: (3:16)

Expanding Equation (3.16), we obtain

¼ Ex μðÞ



¼ Ex

 2μx þ μ



¼ Ex



 2μExðÞþμ

¼ Ex



 2μ

þ μ

¼ Ex



 μ

PðxÞμ

(3:17)

Substituting Equation (3.12) into Equation (3.17), we obtain

x¼0

x! n  xðÞ!

nx

 μ

Note that x

cannot cancel with the terms in x!, but x( x − 1) can. Therefore, we add

and subtract E(x) as shown below:

162

Probability and statistics

x¼0

ðx

 xÞ

x! n  xðÞ!

nx

x¼0

x! n  xðÞ!

nx

 μ

Substituting results from Equation (3.15), we obtain

x¼n

x¼2

xx 1ðÞ

x! n  xðÞ!

nx

þ np  n

;

¼ nn 1ðÞp

x¼n

x¼2

n  2ðÞ!

x  2ðÞ! n  xðÞ!

x2

nx

þ np  n

The summation term is the binomial distribution for n – 2 independent Bernoulli

trials, and sums to 1.

The above equation simpliﬁes as follows :

¼ n

 np

þ np  n

;

¼ np 1  pðÞ:

(3:18)

The mean and the variance of the probability distribution shown in Figure 3.4 is

calculated using Equations (3.15) and ( 3.18), and are 3.5 and 1.05, respectively. The

standard deviation is simply the square root of the variance and is 1.025.

3.4.2 Poisson distribution

The Poisson distribution is a limiting form of the binomial distribution and has

enjoyed much success in describing a wide range of phenomena in the biological

sciences. Poisson distributions are used to describe the probability of rare events

occurring in a ﬁnite amount of time or space (or distance). For example, water-

pollution monitoring involves sampling the number of bacteria per unit volume of

the water body. Increased run-off of phosphate-rich fertilizers is believed to be a

cause of “cyanobacteria blooms” – a rapid growth of this very common bacteria

phylum. Cyanoba cteria produce cyanotoxins, which if ingested can cause gastro-

intestinal problems, liver disorders, paralysis, and other neurological problems. The

concentration of bacteria in a water sample can be modeled by the Poisson distri-

bution. Given the average number of bacteria per milliliter of water obtained from

the water body or aqueous efﬂuent, the Poisson formula can determine the proba-

bility that the concentration of bacteria will not exceed a speciﬁed amount.

Another example of the application of the Poisson distribution in biology is in

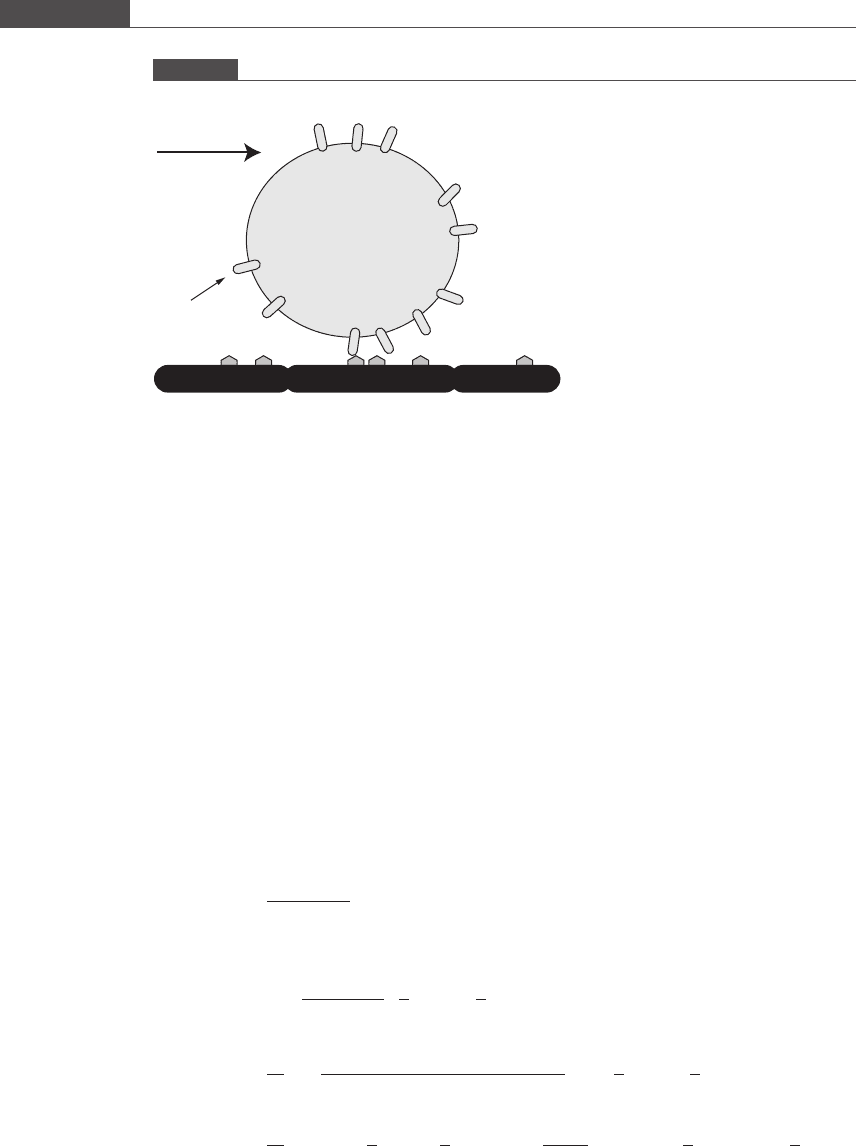
predicting the number of adhesive receptor–li gand bonds formed between tw o cells.

Cells display a wide variety of receptors on their surface. These receptors speciﬁcally

bind to either ligands (proteins/polysaccharides) in the extracellular space or

counter-receptors located on the surface of other cells (see Figure 3.5). When two

cells are brought into close contact by any physical mechanism (e.g. blood cells

contacting the vessel wall by virtue of the local hemodynamic ﬂow ﬁeld), the physical

proximity of adhesion receptors and counter-receptors promotes attachment of the

two cells via bond formation between the complementary receptor molecules.

Leukocytes have counter-receptors or ligands on their surface that allow them to

bind to activated endothelial cells of the vessel wall in a region of inﬂammation. The

activated endothelial cells express selectins that bind to their respective ligand

presented by the leukocyte surface. Selectin–ligand bonds are short-lived, yet their

role in the inﬂammation pathway is critical since they serve to capture and slow

163

3.4 Discrete probability distributions

down the leukocytes so that the downstream events of ﬁrm adhesion, transmigration

through the vessel, and entry into the inﬂamed interstitial tissue can occur. The

attachment of a leukocyte to the vessel wall is termed an adhesion event. The fraction

of cell–cell adhesion events that result from single-bond formation, double-bond

formation, or more can be described by the Poisson distribution.

We are interested in events that take place within a certain time interval or

speciﬁed volume. The time period or volume can be partitioned into many smaller

subintervals so narrow that only one event can occur (e.g. death of a patient, failure

of medical equipment, presence of a single microscopic organism) in that sub-

interval. If p is the probabil ity that the event (or “success”) occurs in the subinterval,

and there are n subintervals in the speciﬁed time period or volume, then , as long as p

does not vary from subinterval to subinterval, i.e. the events in each subinterval are

independent, the experimental outcome will be governed by the binomial probability

distribution.

If n → ∞,andγ = np (mean of the binomial distribution), then the binomial

probability for x successes out of n independent trials

PxðÞ¼

x! n  xðÞ!

ð1  pÞ

nx

becomes

PxðÞ¼lim

n!∞

x! n  xðÞ!



1 



nx

lim

n!∞

n  1ðÞn  2ð Þðn  x þ 1Þ

x1

1 



1 



x

lim

n!∞

1 



1 



 1 

x  1



lim

n!∞

1 



lim

n!∞

1 



x

The lim

n!∞

1  γ=nðÞ

when expanded using the binomial theorem is the Taylor series

expansion (see Section 1.6 for an explanation on the Taylor series) of e

γ

. Then

Figure 3.5

Leukocyte transiently attached to the vascular endothelium via selectin bonds.

Selectin–

ligand

Selectins expressed

by endothelial cells

Vascular wall

Leukocyte

Direction of flow

164

Probability and statistics

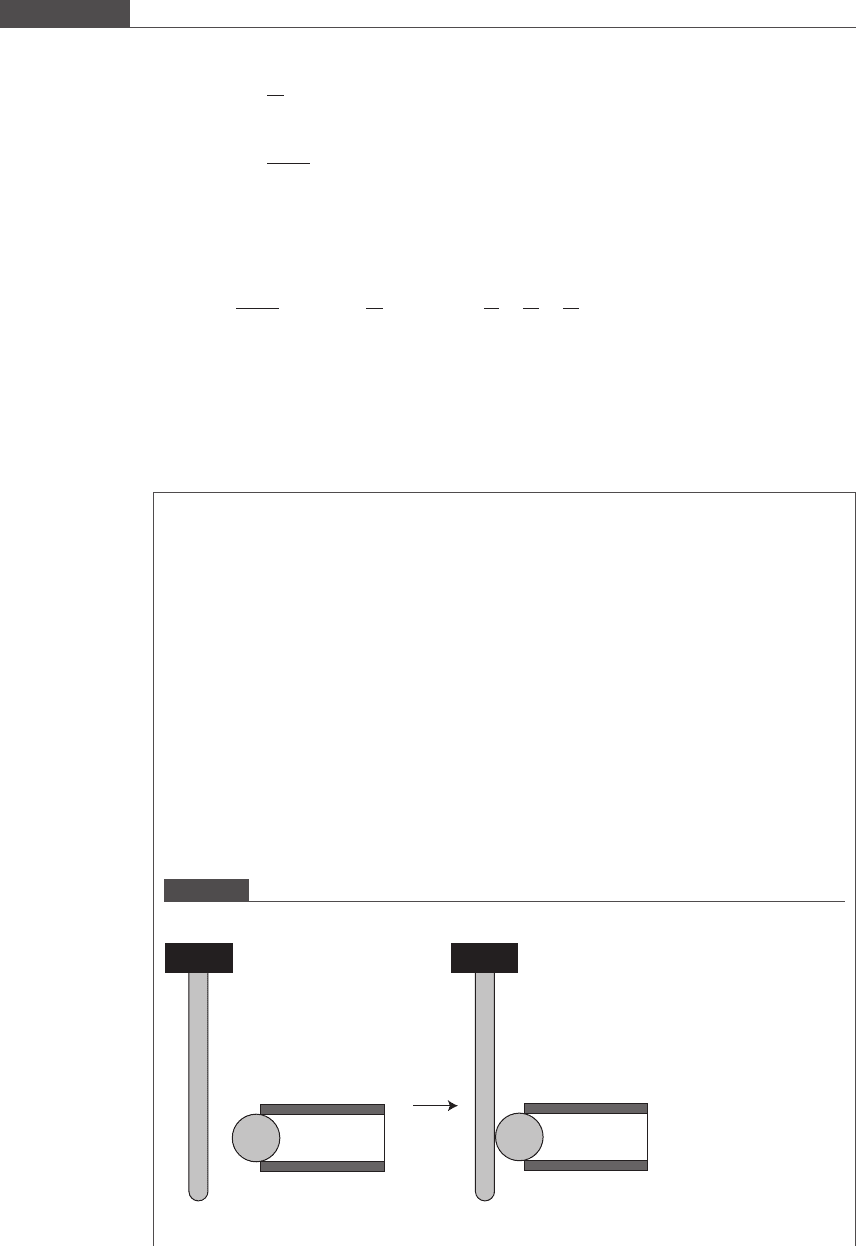
PxðÞ¼

 1  e

γ

 1

γ

: (3:19)

The summation of the discrete Poisson probabilities obtained from a Poisson

probability distribution for all x =0, 1, 2, ..., ∞ must equal 1. This is easily

shown to be true:

∞

x¼0

γ

¼ e

γ

∞

x¼0

¼ e

γ

1 þ

þ



¼ e

γ

¼ 1:

The mean and variance of the Poisson probability distribution are given by

μ ¼ γ; σ

¼ γ: (3:20)

The proof of this derivation is left as an exercise (see Problem 3.6).

Box 3.3 Poisson distribution of the number of bonds formed during transient

leukocyte–vessel wall attachments

Bioadhesive phenomena involve the attachment of cells to other cells, surfaces, or extracellular matrix

and are important in angiogenesis, blood clotting, metastasis of cancer cells, and inflammation. Several

experimental techniques have been devised to characterize and quantify the adhesive properties of

biological macromolecules. Of particular interest to bioadhesion researchers are the effects of varying

intensities of pulling force on bond strength. Force application on receptor–ligand bonds mimics the

hydrodynamic forces that act upon blood cells or cancer cells that stick to surfaces or other cells under

flow.

One experimental set-up used to study leukocyte ligand binding to selectins uses a glass micro-

cantilever coated with E-selectin molecules (Tees et al., 2001). A microsphere functionalized with the

selectin ligand is pressed against the cantilever to ensure sufficient contact between the biomolecules

(see Figure 3.6). The microsphere is then retracted away from the cantilever, which undergoes visually

measurable deflection.

Figure 3.6

An adhesive microcantilever reversibly attaches to a retracting microsphere.

Microcantilever

fiber

Microsphere

Micropipette

Contact followed by retraction

165

3.4 Discrete probability distributions

3.5 Normal distribution

The normal distribut ion is the most widely used probability distribution in the ﬁeld

of statistics. Many observations in nature such as human height, adult blood

pressure, Brownian motion of colloidal particles, and human intelligence are

found to ap proximately follow a normal distribution. The normal distribution sets

itself apart from the previous two discrete probability distributions discussed in

Section 3.4, the binomial and Poisson distribut ion, in that the normal distribution is

continuous and is perfectly symmetrical about the mean. This distribution is com-

monly referred to as a “bell-shaped curve” and is also described as the Gaussian

distribution. Abraham De Moivre (1667–1754) was the ﬁrst mathematician to

The bead contacts the cantilever surface for a fixed duration; this time interval can be subdivided into

many smaller intervals over which the probability of a single bond forming is some small number p and

the probability of multiple bonds forming over the very small time interval is practically 0. It was

determined that 30% of the contact events between the microsphere and the microcantilever resulted in

adhesion events. An adhesion event is defined to occur when the microsphere attaches to the

microcantilever and causes a measurable deflection when retraction begins. Mathematically, we write

0ðÞ¼0:3orPN

¼ 0ðÞ¼0:7:

The distribution of the number of bonds N

that form between the two opposing surfaces follows the

Poisson formula:

ðÞ

γ

;

where γ is the mean number of bonds, N

, that form during contact. Note that N

is calculated by

using the known result for PN

¼ 0ðÞ:

¼ 0ðÞ¼0:7 ¼ e

 N

;

¼ln 0:7 ¼ 0:357:

Now we are in a position to calculate PN

0ðÞ:

¼ 1ðÞ¼

0:357

0:357

¼ 0:250;

¼ 2ðÞ¼

0:357

0:357

¼ 0:045;

¼ 3

ðÞ

0:357

0:357

¼ 0:005:

The fraction of adhesion events that involve a single bond, double bond, or triple bond PN

0ðÞare

0.833, 0.15, and 0.017, respectively. How did we calculate this? Note that while the fractional frequency

of formation of one, two, and three bonds sum to 1 (0.833 + 0.15 + 0.017 = 1), this is an artifact of

rounding, and the probability of formation of greater number of bonds (>3) is small but not quite zero.

The mean number of bonds N

calculated here includes the outcome of contact events that result

in no binding, N

= 0. What is the mean number of bonds that form if we are only to include contact

events that lead to adhesion? Hint: Start out with the definition of mean N

hi(see Equation (3.14)).

Answer: 1.19.

166

Probability and statistics