King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

Using MATLAB

Statistics Toolbox provides an inverse cumulative distribution function, inv, for a

variety of probability distributions. The inv function accepts cumulative probabil-

ity values P and returns the corresponding values of the random variable x with

respect to a speciﬁc probability distribution. Of parti cular interest to us is the

norminv function. The syntax for norminv is

x = norminv(P, mu, sigma)

where mu and sigma are parameters of the normal distribution and P is the vector of

probabilities at which the corresponding value(s) of the random variable x is

evaluated.

If we want to know the value of the z statistic that denotes the 95th percentile, we

compute

x = norminv(0.95, 0, 1)

MATLAB output:

1.6449

On the other hand, if we want to determine the z values that bracket 0.95 of the

enclosed area symmetrically about μ, we type

x = norminv([0.025 0.975], 0, 1])

MATLAB output:

-1.9600 1.9600

3.5.5 Confidence intervals using the z statistic and the t statistic

Since μ and σ of a population are usually not known in any experiment, we must use

data from a sample to calculate



x; s

, and s, which serve as our estimates of the

Figure 3.11

Areas under the standard normal curve.

0–1

–2

–3 1

68.3 %

observations

95.4 %

observations

99.7 %

observations

Standard normal curve

177

3.5 Normal distribution

population statistics. The primary goal in an experiment is to estimate the mean of

the population under consideration. Because discr epancies exist between the stat-

istical properties of the sample and that of the entire population, uncertainty is

associated with our sample-derived population estimates, and we proceed to make

statistical inferences. Based on the data available, we infer the statistical properties of

the population. The statistical estimates that are derived from the data or sample

should be accompani ed by a probability and a conﬁdence interval, which convey,

respectively, the level of accuracy and precision with whi ch we have obtained our

estimate. Inferential statistics is the branch of statistics that deals with obtaining and

using sample-derived estimates of population characteristics to draw appropriate

conclusions about the reference population. We now shift our focus to the topic of

statistical inference.

Statistical inference has two broad purposes as detailed below.

(1) Estimation. To estimate a population parameter (e.g. mean, median, or variance)

from the data con tained in a random sample drawn from the population. The

statistic calculated from the sample data can be of two types:

(a) point estimate, or a single numeric value that estimates the population

parameter;

(b) interval estimate, or a set of two values that specify a range called a conﬁdence

interval that is believed to contain the population parameter. A probability is

speciﬁed along with the interval to indicate the likelihood that the interval

contains the parameter being estimated.

(2) Hypothesis testing. To draw a conclusion concerning one or more populations based

on data obtained from samples taken from these populations. This topic is discussed

in Chapter 4.

In this and the following sections, we learn how to estimate a population parameter

by constructing a conﬁdence interval. A conﬁdence interval is an interval estimate of

a population parameter, as opposed to a point estimate (single number) , which you

are more familiar with. When working with samples to derive population estimates,

a point estimate of a parameter, e.g.



x or s

, is not sufﬁcient. Wh y? Even if the

measurements associated with our data are very accurate or free of measurement

error, sample statistics derived from the measurements are still prone to sampling

error. It is very likely that point estimates of a parameter based on our samples will

not be correct since the sampl e is an incomplete representation of the entire

population.

The distribution of sample means



x is a frequency distribution plot of all possible

values of



x obtained when all possible samples of the same size are drawn from a

reference population, and is called the sampling distribution of the mean.When

samples are drawn from a normal population (i.e. x is distributed as N μ; σðÞwithin

the population), the sampling distribution of the mean will also be normal, with a

mean equal to μ and standard deviation equal to the standard error of the mean

(SEM) σ=

ﬃﬃﬃ

. The sample mean can theoretically lie anywhere along the normal

curve that represents the sampling distribution of the mean. The sampling error or

uncertainty in our estimate of μ is conveyed by the SEM = σ=

ﬃﬃﬃ

, which measures

the spread of distribution of the sample means.

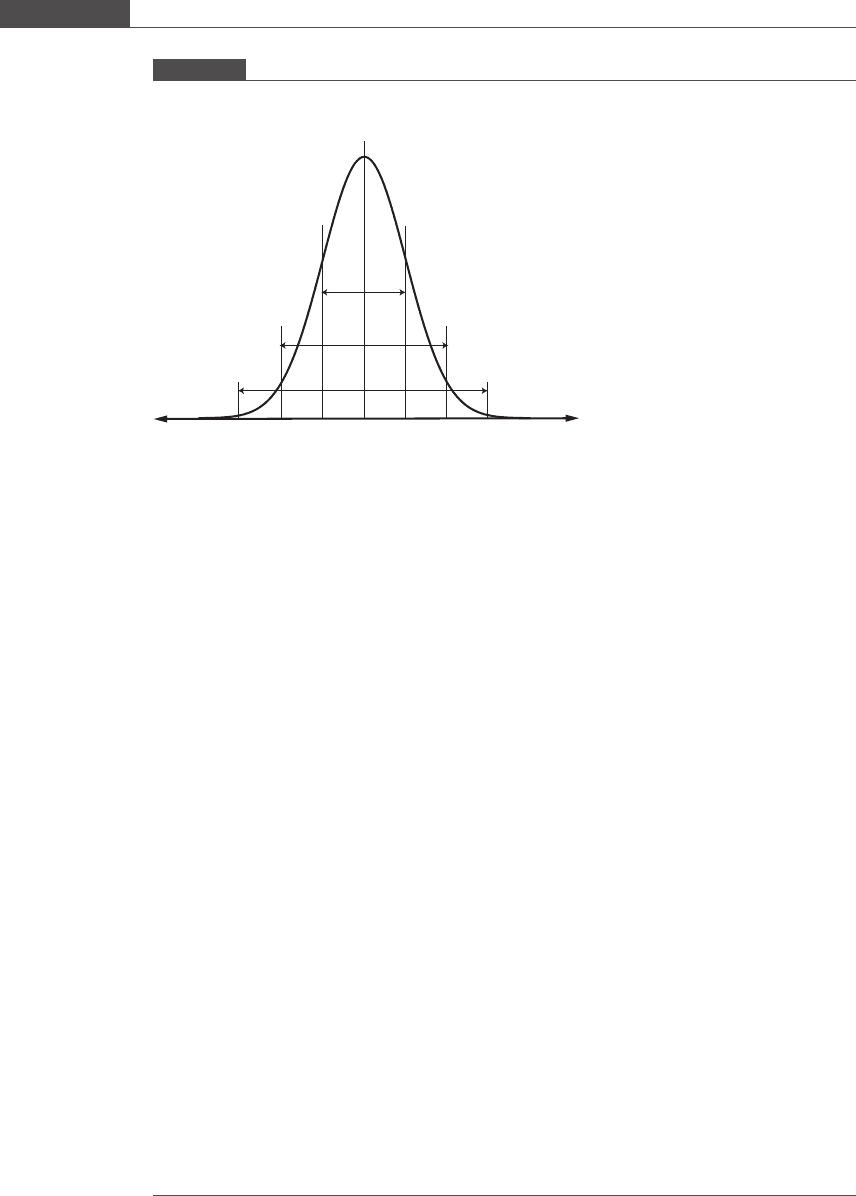
For any normally distributed population, 95% of the measurements lie within

±1.96 standard deviations (z = 1.96) from the mean. Speciﬁcally, in the case of

the distribution of sample means, 95% of the sample means lie within a distance

of ±1.96σ=

ﬃﬃﬃ

from μ. Of course, we do not know the actual population statist ics.

178

Probability and statistics

Let’s assume for the time being that we have knowledge of σ. We cannot determine

the interval μ  1:96σ=

ﬃﬃﬃ

that will contain 95% of the sampling means, since we do

not know μ. But we can determine the interval



x  1:96σ=

ﬃﬃﬃ

and we can make the

following statement.

If the interval μ  1:96 σ=

ﬃﬃﬃ

contains 95% of the sample means, then 95% of the intervals



x  1:96 σ=

ﬃﬃﬃ

must contain the population mean.

The importance of this statement cannot be overemphasized, so let’s discuss this further.

Of all possible samples of size n that can be drawn from a population of mean μ and

variance σ

, 95% of the samples will possess a mean



x that lies within 1:96 σ=

ﬃﬃﬃ

standard deviations from the population mean μ. Mathematically, we write this as

P μ  1:96

ﬃﬃﬃ



μ þ 1:96

ﬃﬃﬃ



¼ 0:95:

We subtract



x and μ from all sides of the inequality. Then, taking the negative of each

side, we obtain



x  1:96

ﬃﬃﬃ



x þ 1:96

ﬃﬃﬃ



¼ 0:95:

Therefore, 95% of all samples obtained by repeated sampling from the population

under study will have a mean such that the interval



x  1:96σ=

ﬃﬃﬃ

includes the

population mean μ. Figure 3.12 illustrates this. On the other hand, 5% of the sample

means



x lie further than 1:96σ=

ﬃﬃﬃ

units from the population mean. Then, 5% of the

intervals,



x  1:96σ=

ﬃﬃﬃ

, generated by all possible sample means, will not contain the

population mean μ. Therefore, if we conclude that the population mean lies within

1.96 standard deviations from our current sample mean estimate, we will be in error

5% of the time.

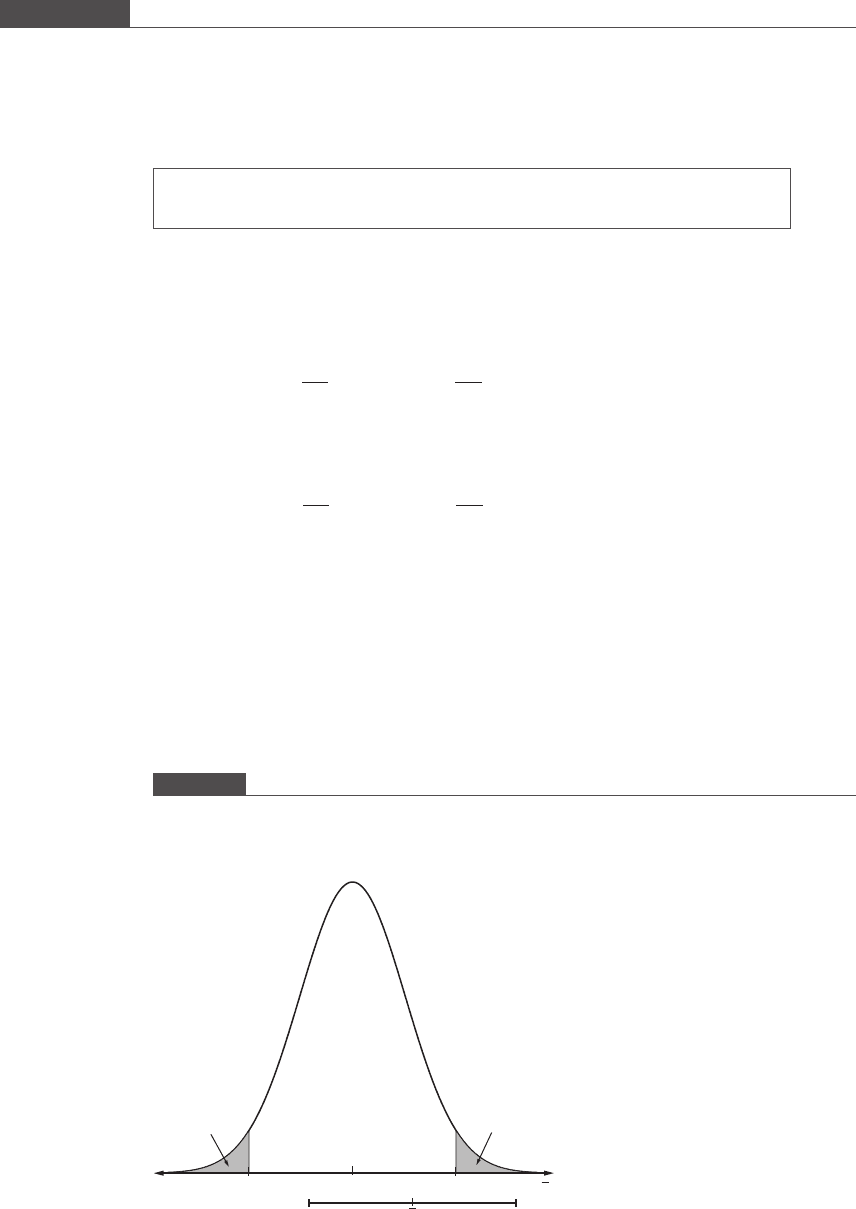
Figure 3.12

The sampling distribution of all sample means



x derived from a population that exhibits an Nðμ; σÞ distribution. The

areas under the curve that lie more than 1.96 standard deviations on either side from the population mean μ, i.e. the

extreme 5% of the population, are shaded in gray. A 95% confidence interval for μ is drawn for the sample mean



(1 – α) = 0.95

α/2 = 0.025

–1.96σ

95% confidence interval for μ

/2 = 0.025

1.96

179

3.5 Normal distribution

In most cases, we have only one sample mean obtained from our experiment (our

sample). We infer from our data with 95% conﬁdence that the interval



x  1:96σ=

ﬃﬃﬃ

contains the true population mean.



x  1:96σ=

ﬃﬃﬃ

is called the 95% confidence interval for the population mean μ, and the endpoints of

this interval are called the 95% confidence limits.

When we construct a 95% conﬁdence interval, it is inferred that any mean value

lying out side the conﬁdence interval belongs to a population that is signiﬁcantly

different from the population deﬁned by the 95% conﬁdence interval for μ. Since 5%

of the time the conﬁdence interval constructed from the sample mean



x will not

contain its true population mean μ, we will wrongly assert a signiﬁcant difference

between the sample and the population from which the sample is derived 5% of the

time. The accuracy, or level of conﬁdence, expresse d in the terms of probabilities

such as 90%, 95%, or 99% conﬁdence, with which a conﬁdence interval is con-

structed, depends on the chosen signiﬁcance level α.

Let’s have a second look at the sampling distribution for the sample mean



shown in Figure 3.12. The interval μ  1:96σ=

ﬃﬃﬃ

excludes 5% of the area under the

curve located within the two tails. This area (shaded in gray) corresponds to a 0.05

probability that a sample mean obtained from a population wi th mean μ will be

excluded from this interval. In other words, the signiﬁcance level for this interval is

set to α = 0.05. The excluded area within both tails is equally distributed and is α/2 at

either end, i.e. 2.5% of the sample means are located to the right of the interval and

the other 2.5% are situated on the left. The critical z values that satisfy the cumu-

lative probability equations Φ zðÞ¼α=2; Φ zðÞ¼1  α=2 are z

α/2

= –1.96 and z

(1−α/2)

= 1.96. The area under the curve within the interval μ  1:96σ=

ﬃﬃﬃ

is 1 – α. As the

signiﬁcance level α is reduced, the interval about μ for means of samples drawn from

the same population widens and more sample means are included within the interval

μ  z

1α=2

ðσ=

ﬃﬃﬃ

Þ.Ifα = 0.01, then 99% of all samples means are included within the

interval centered at μ. When we create a 100 1  αðÞ% con ﬁdence interval for μ using

a sample mean



x , we must use z

α/2

and z

(1−α/2)

to deﬁne the width of the interval.

Although it is a common choice among scientists and engineers, it is not necessary

to restrict our calculations to 95% conﬁdence intervals . We could choose to de ﬁne

90% or 99% conﬁdence intervals , depending on how small we wish the interval to be

(precision) and the required accuracy (probability associated with the conﬁdence

interval). Table 3.5 lists the z values associated with different levels of signiﬁcance α,

when the conﬁdence interval is symmetrically distributed about the sampl e mean

(two-tailed distribution).

Table 3.5. The z values associated with different levels of signiﬁcance for a two-sided

distribution

Level of signiﬁcance, α Type of conﬁdence interval z

α/2

, z

(1−α/2)

0.10 (α/2 = 0.05) 90% ±1.645

0.05 (α/2 = 0.25) 95% ±1.96

0.01 (α/2 = 0.005) 99% ±2.575

0.005 ( α/2 = 0.0025) 99.5% ±2.81

0.001 ( α/2 = 0.0005) 99.9% ±3.27

180

Probability and statistics

The 100(1 − α)% confidence interval for μ for a two-sided distribution is



x  z

1α=2

ﬃﬃﬃ

When we do not know the population standard deviation σ,wemakeuseofthe

sample-derived standard deviation to obtain the best estimate of the conﬁdence interval

for μ, i.e.



x  z

1α=2

ðs=

ﬃﬃﬃ

Þ. Large sample sizes will usually yield s as a reliable estimate

of σ. However, small sample sizes are prone to sampling error. Estimates of SEM that

are less than their true values will underestimate the width of the conﬁdence interval.

William Sealy Gosset (1876–1937), an employee of Guinness brewery, addressed this

problem. Gosset constructed a family of t curves, as modiﬁcations of the normal curve.

The shape of each t curve is a function of the degrees of freedom f associated with the

calculation of the standard deviation, or alternatively a function of the sample size.

Recall that for a sample of size n, the degrees of freedom or independent data points

available to calculate the standard deviation is n – 1. (Note that if there is only one data

point available, we have no information on the dispersion within the data, i.e. there are

Box 3.4 Bilirubin level in infants

Red blood cells have a normal lifespan of 3–4 months. Bilirubin is a component generated by the

breakdown of hemoglobin and is further processed in the liver. Bilirubin contains a yellow pigment.

Build up of bilirubin in the body due to liver malfunction gives skin a yellowish hue. Bilirubin is removed

from fetal blood through placental exchanges. Once the child is born, the immature newborn liver must

begin processing bilirubin. The liver is initially unable to keep up with the load of dying red blood cells.

Bilirubin levels increase between days 2 and 4 after birth. Bilirubin concentrations usually fall

substantially by the end of the first week. Many other factors can aggravate bilirubin concentration in

blood during the first week of life. High concentrations of bilirubin can have severely adverse effects,

such as permanent hearing loss, mental retardation, and other forms of brain damage.

The average measured bilirubin concentration in 20 newborns on day 5 was 6.6 mg/dl. If the bilirubin

levels in 5-day-old infants are normally distributed with a standard deviation of 4.3 mg/dl, estimate μ by

determining the 95% and 99% confidence intervals for the population mean bilirubin levels.

The 95% confidence interval for the mean bilirubin level in 5-day-old infants is



x  1:96

ﬃﬃﬃ

;

i.e.

6:6  1:96

4:3

ﬃﬃﬃﬃﬃ

¼ 4:7; 8:5:

We are 95% confident that the mean bilirubin level of 5-day-old infants lies between 4.7 and 8.5 mg/dl.

The 99% confidence interval for the mean bilirubin level in 5-day-old infants is



x  2:575

ﬃﬃﬃ

;

i.e.

6:6  2:575

4:3

ﬃﬃﬃﬃﬃ

¼ 4:1; 9:1:

We are 99% confident that the mean bilirubin level of 5-day-old infants lies between 4.1 and 9.1 mg/dl.

181

3.5 Normal distribution

no degrees of freedom.) Gosset published his work under the pseudonym “Student” to

hide his true identity since there had been a publication freeze within the Guinness

company. For this reason, the t distribution is widely associated with the name

“Student.” If the population distribution is estimated using sample statistics, Nð



x; sÞ,

then the conﬁdence interval for the population μ for any desired signiﬁcance level can

be calculated using the t statistic.Thet statistic is given by

t ¼



x  μ

ﬃﬃﬃ

: (3:35)

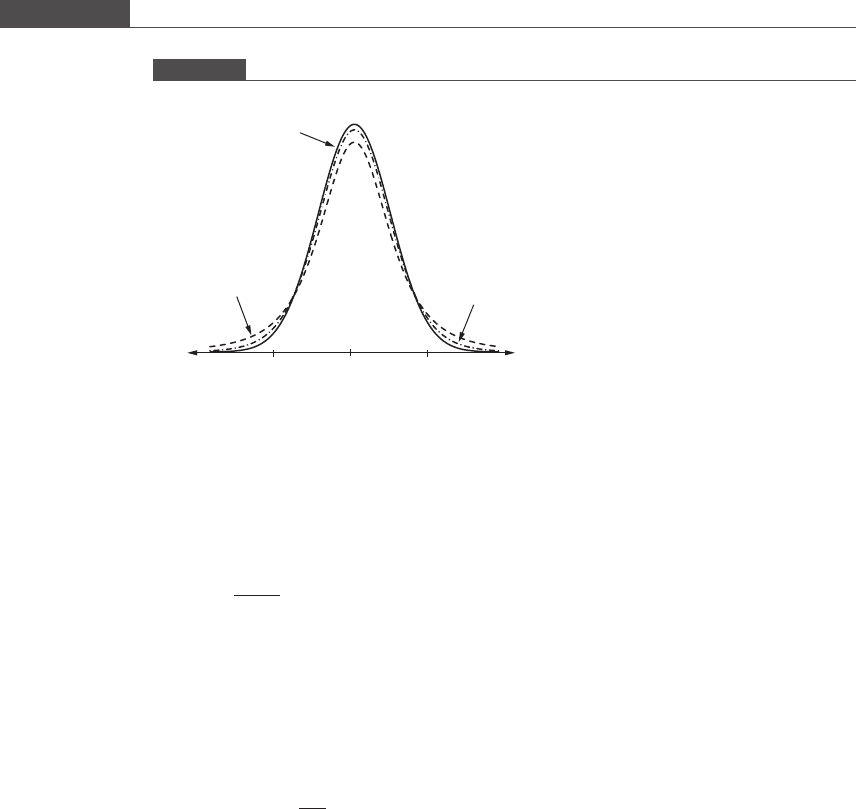
The t statistic follows the t distribution, which features the characteris tic symmetric

bell-shape of the normal distribution except with bulkier tails and a shorter central

region. The exact shape of the t distribution is dependent on the sample size n (or

degrees of freedom, f ¼ n  1) and approaches the normal distribution as n → ∞.

Figure 3.13 illustrates the shape dependence of the t distribution on sample size.

The desired conﬁdence interval for μ is calculated as



x  t

1α=2; f

ﬃﬃﬃ

;

where t

1α=2; f

is the t statistic for a sample size n, degrees of freedom f, and a

signiﬁcance level equal to α for a two-t ailed (two-sided) distribution. In a two-tailed

distribution, the areas of signiﬁcance are split symm etrically on both sides of the

probability distribution curve at both ends (tails). The critical value of the t statistic,

i.e. t

1α=2; f

, is always greater than the corresponding (for the same sample size)

critical z value z

1α=2

for the same signiﬁcance level and approaches z

1α=2

for n → ∞.

Because Gossett adopted the pseudonym of “Student” under which he published his

work, the t curves are commonly known as “Student’s t distributions.” Wh ile the use

of t distributions is strictly valid when sampling is done from a normal population,

many researchers apply t distributions for assessing non-normal populations that

display at least a unimodal (single-peaked) distribution.

Using MATLAB

The MATLAB Statistics Toolbox contains several functions that allow the user to

perform statistical analysis using Student’s t distribution. Two useful functions are

tcdf and tinv. Their respective syntax are given by

Figure 3.13

Distributions of the z and t statistics.

–1.96 1.96

t distribution

= 4

t distribution

= 11

z (standard normal)

distribution

= ∞

182

Probability and statistics

p = tcdf(t, f)

t = tinv(p, f)

where f is the degrees of freedom, and t and p have their usual meanings (see the

discussion on normcdf and norminv).

The function tcdf calculates the cumulative probability (area under the t curve;

see Equation (3.34)) for values of t, a random variable that follows Student’s t

distribution, and tinv calculates the t statistic corresponding to the cumulative

probability speciﬁed by the input parameter p.

3.5.6 Non-normal samples and the central-limit theorem

In Sectio ns 3.5.4 and 3.5.5 we assumed that the population from which our samples

are drawn is normally distributed. Often, you wi ll come across a histogram or

frequency distribution plot that shows a non-normal distribution of the data. In

such cases, are the mathematical concepts developed to analyze statistical informa-

tion obtained from normally distributed populations still applicable? The good news

is that sometimes we can use the normal distribution and its accompanying simplify-

ing characteristics to estimate the mean of populations that are not normally

distributed.

The central-limit theorem states that if a sample is drawn from a non-normally distributed population

with mean μ and variance σ

, and the sample size n is large (n > 30), the distribution of the sample

means will be approximately normal with mean μ and variance σ

/n.

Box 3.5 Shoulder ligament injuries

An orthopedic research group studied injuries to the acromioclavicular (AC) joint and coracoclavicular

(CC) joint in the shoulder (Mazzocca et al., 2008). In the study, AC and CC ligaments were isolated from

fresh-frozen cadaver shoulders with an average age of 73 (±13) years. Ten out of 40 specimens were

kept intact (no disruption of the ligament) and loaded to failure to assess normal failure patterns. The

mean load to failure of the CC ligaments was 474 N, with a standard deviation of 174 N. We assume that

these ten specimens constitute a random sample from the study population. If it can be assumed that

the population data are approximately normally distributed, we wish to determine the 95% confidence

interval for the mean load to failure.

The sample statistics are:



x = 474, s = 174, n = 10, f = n – 1=9.

We estimate the SEM using statistics derived from the sample:

SEM ¼

ﬃﬃﬃ

174

ﬃﬃﬃﬃﬃ

¼ 55:0:

We use the tinv function to calculate the critical value of the t statistic, which defines the width of

the confidence interval:

t = tinv(0.975, 9);

Then, −t

0.025

= t

0.975

= 2.262 for nine degrees of freedom.

The desired 95% confidence interval for mean load to failure of the intact CC ligament is thus

given by

474 ± 2.262(55.0) or 349 N, 598 N.

183

3.5 Normal distribution

Therefore, we can apply statistical tools such as the z statistic and the Student’s t

distribution, discussed in the previous section, to analyze and interpret non-normally

distributed data. How large must the sample size be for the central-limit theorem to

apply? This depends on the shape of the population distribution; if it is exactly normal,

then n can be of any value. As the distribution curve deviates from normal, larger values

of n are required to ensure that the sampling distribution of the means is approximately

normal. Remember that random sampling requires that n  N (population size). Since

N is often very large (N >10

) in biologi cal studies, a large sample size say of n =100or

500 will not approach N (e.g. the number of bacteria in the human gut, number of coffee

drinkers in Spain, or number of patients with type II diabetes).

If the data are grossly non-normal, and the applicability of the central-limit

theorem to a limited sample size is doubtful , then we can often use mathematical

techniques to transform our data into an approximately normal distribution. Some

Box 3.6 Brownian motion of platelets in stagnant flow near a wall

Platelets, or thrombocytes, the smallest of the three main blood cell types, are discoid particles

approximately 2 μm in diameter. At the time of vascular injury, platelets are recruited from the

bloodstream to the exposed subendothelial layer at the lesion, where they promptly aggregate to seal

the wound. These microparticles fall within the realm of Brownian particles, primarily due to their

submicron thickness (~0.25 μm). Brownian motion is an unbiased random walk with normal distribu-

tion. The mean displacement of a Brownian particle in the absence of bulk flow is 0. Mody and King

(2007) performed a computational study to investigate the Brownian motion of a platelet in order to

quantify its impact on platelet flow behavior and platelet adhesive behavior when bound to a surface or

to another platelet. The platelet was placed at various heights H from the surface in the absence of an

external flow-field. The duration of time required for the platelet to contact the surface by virtue of its

translational and rotational Brownian motion was determined (see Figure 3.14 ).

Two hundred surface-contact observations were sampled for each initial platelet centroid height.

Figure 3.15 shows a histogram of the time taken T

for a platelet to contact the surface by virtue of

Figure 3.14

Flow geometry in which a single platelet (oblate spheroid of aspect ratio = 0.25) is translating and rotating in

stagnant fluid by virtue of translational and rotational Brownian motion near an infinite planar surface. At the instant

shown in the figure, the platelet is oriented with its major axis parallel to the surface and its centroid located at a

distance H from the surface.

Planar wall

Spheroid axis of revolution

Three-dimensional

coordinate system

Major axis

184

Probability and statistics

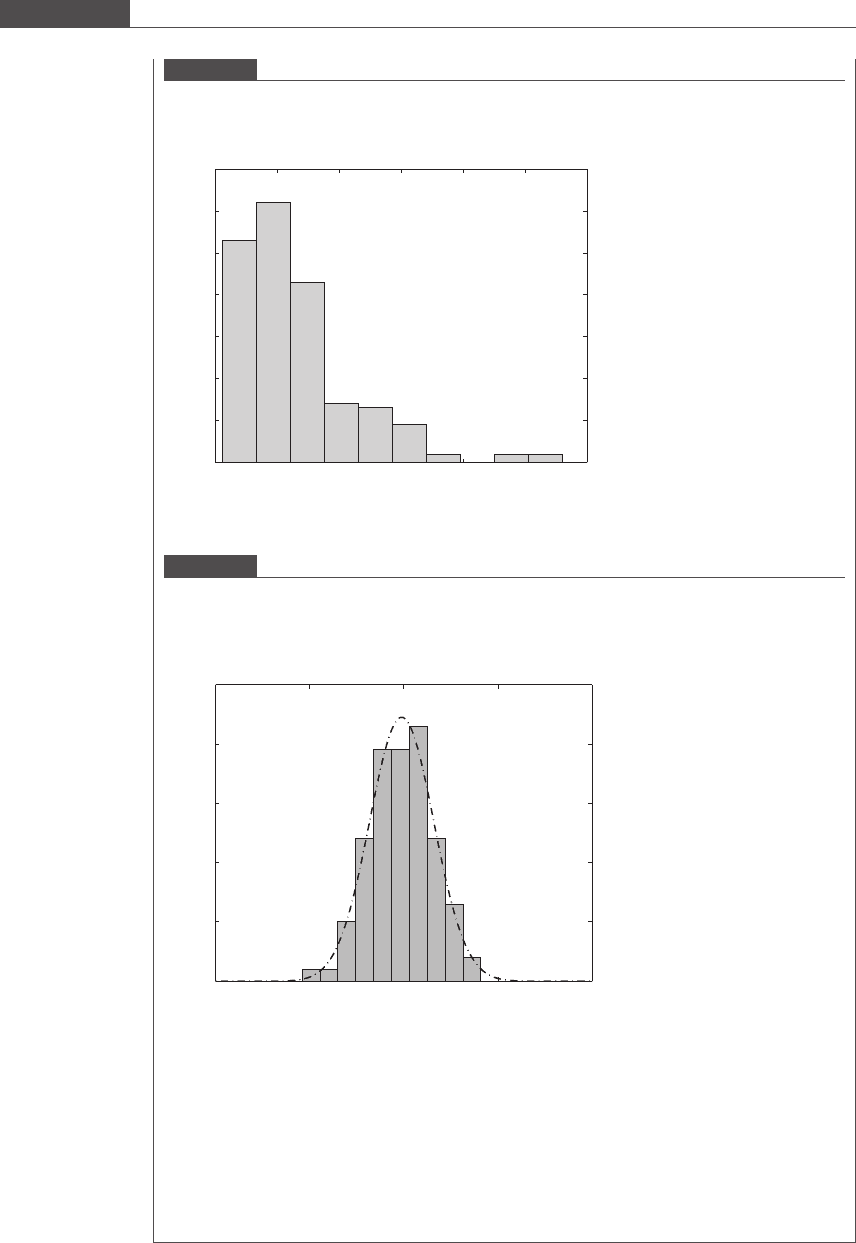
Figure 3.16

Histogram of the log of the time taken T

for a platelet to contact the surface when undergoing translational and

rotational Brownian motion in a quiescent fluid for initial height H = 0.625. A normal curve of equivalent μ and σ is

superimposed upon the histogram.

0 2 4 6 8

log(time until surface contact (s))

Number of events

H = 0.625

Brownian motion only, for an initial centroid height H = 0.625. The mean and variance of the data are 65

and 2169. The distribution curve has an early peak and a long tail.

Since we want to center the distribution peak and equalize the tails on both sides of the peak, we

perform a natural logarithm transformation of the data. Figure 3.16 shows that the transformed data have

an approximately log normal distribution. The mean and variance of the transformed distribution is

3.95 and 0.47. A normal curve with these properties and area equal to that enclosed by the histogram is

superimposed upon the histogram plotted in Figure 3.16. The transformation has indeed converted the

heavily skewed distribution into an approximately normal distribution.

Figure 3.15

Histogram of the time taken T

for a platelet to contact the surface when undergoing translational and rotational

Brownian motion in a quiescent fluid for initial height H = 0.625.

0 50 100 150 200 250 300

H = 0.625

Time until surface contact (s)

Number of events

185

3.5 Normal distribution

common transformations involve converting the data to log scale (ln x), calculating

the square root (

ﬃﬃﬃ

), or inverting the data (1/x).

3.6 Propagation of error

All experimental measurements and physical observations are associated with some

uncertainty in their values due to inherent variability associated with natural phe-

nomena, sampl ing error, and instrument error. The error or variability in the

measurements of a random variable is often reported in terms of the standard

deviation. When arithmetically combining measurements in a mathematical

Box 3.7 Nonlinear (non-normal) behavior of physiological variables

Physiological functioning of the body, such as heart rate, breathing rate, gait intervals, gastric

contractions, and electrical activity of the brain during various phases of sleep, are measured to

ascertain the state of health of the body. These mechanical or electrical bodily functions fluctuate with

time and form chaotic patterns when graphed by e.g. an electrocardiograph or an electroencephalo-

graph. It has been long believed that a healthy body strives to maintain these physiological functions at

certain “normal” values according to the principle of homeostasis. The fluctuations that are observed in

these rates are the result of impacts on the body from various environmental factors. Fluctuations in

heart rate or stride rate that occur are primarily random and do not exhibit any pattern over a long time.

Along this line of reasoning, it is thought that every human body may establish a slightly different normal

rate based on their genetic make-up. However, all healthy people will have their bodily functioning rates

that lie within a normal range of values. Thus, any rate process in the body is quantified as a mean value,

with fluctuations viewed as random errors or noise.

Recently, studies have uncovered evidence showing that the variability in these physiological rate

processes is in fact correlated over multiple time scales. Physiological functions seem to be governed

by complex processes or nonlinear dynamical processes, which produce chaotic patterns in heart rate,

walking rate, breathing rate, neuronal activity, and several other processes. Chaotic processes, which

are complex phenomena, are inherently associated with uncertainty in their outcomes. Complex

systems are sensitive to initial conditions and slight random events that influence the path of the

process. “The butterfly effect” describes an extreme sensitivity of a process to the initial conditions such

that even a small disturbance or change upfront can lead to a completely different sequence of events as

the process unfolds. This phenomenon can result from processes governed by nonlinear dynamics and

was initially discovered by Edward Lorenz, a meteorologist who was instrumental in developing modern

chaos theory.

The variability in our physiological functioning is neither completely random (noise) nor is it

completely correlated or regular. In fact, a state of good health is believed to require processes that

are correlated to an optimal degree such that both randomness and memory retained over numerous

time scales play synergistic roles to ensure versatility and robustness of our body functions (West,

2006). Disease states are represented by a loss of variability or complexity. For example, heart failure

results from either a poor oxygen supply to the heart or defective or weak muscles and/or valves due to

previous disease or congenital defects. During heart failure, the heart is incapable of pumping blood

with sufficient force to reach the organs. Heart rate during heart failure is characterized by loss of

variability, or, in other words, increasing regularity and loss of randomness (Goldberger et al., 1985).

Aging also appears to be synonymous with the onset of increasing predictability in rate processes and

loss of complexity or robustness necessary for survival (Goldberger et al., 2002). For certain physio-

logical processes, much information lies in the observable chaotic patterns, which convey the state of

health and should not be discarded as noise. Such variability cannot be described by simple normal

distributions, and instead can be more appropriately represented by scale-free or fractal distributions.

Normal distributions are suitable for linear processes that are additive and not multiplicative in nature.

186

Probability and statistics