King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB
Подождите немного. Документ загружается.


calculation, the combined error must also be calculated. The end result of a math-
ematical calculation that combines one or more random variables should be
reported in terms of the mean value of the calculated result and the standard
deviation associated with it. In this section, we derive the mathematical rules for
combining measurements associated with error.
Let x
i
and y
i
be two random variables or measurements with mean values of
x and
y and associated variances s
2
x
and s
2
y
, respectively, where
s
2
x
¼
1
n 1
X
n
i¼1
x
i
xðÞ
2
and s
2
y
¼
1
n 1
X
n
i¼1
y
i
yðÞ
2
;
1 i n. Also let C
1
and C
2
be two known constants.
3.6.1 Addition/subtraction of random variables
Consider the general linear combination z
i
¼ C
1
x
i
þ C
2
y
i
. We would like to derive
the equations that relate
z and s
2
z
to our statistical estimates for x and y.
We begin by determining the mean value of z:
z ¼
1
n
X
n
i¼1
z
i
:
Substituting the functional dependence of z on x and y:
z ¼
C
1
n
X
n
i¼1
x
i
þ
C
2
n
X
n
i¼1
y
i
;
z ¼ C
1
x þ C
2
y: (3:36)
Next, we determine the variance associated with z:
s
2
z
¼
1
n 1
X
n
i¼1
z
i
zðÞ
2
¼
1
n 1
X
n
i¼1
ðz
2
i
z
2
Þ
(from Equat ion (3.30)). Squa ring z
i
,
z
2
i
¼ C
2
1
x
2
i
þ C
2
2
y
2
i
þ 2C
1
C
2
x
i
y
i
:
Squaring Equation (3.36),
z
2
¼ C
2
1
x
2
þ C
2
2
y
2
þ 2C
1
C
2
x
y:
Substituting the expressions for z
2
i
and
z
2
into that for s
2
z
, we obtain
s
2
z
¼
1
n 1
X
n
i¼1
C
2
1
x
2
i
x
2
þ C
2
2
y
2
i
y
2
þ 2C
1
C
2
x
i
y
i
x
yðÞ
¼ C
2
1
s
2
x
þ C
2
2
s
2
y
þ
2C
1
C
2
n 1
X
n
i¼1
x
i
y
i
x
yðÞ:
The last term in the above equation,
s
2
xy
¼
1
n 1
X
n
i¼1
x
i
xðÞy
i
yðÞ¼
1
n 1
X
n
i¼1
x
i
y
i
x
yðÞ;
is called the covariance of x and y. The covariance of x and y is defined as
σ
2
xy
¼ Eð x
i
μ
x
ðÞðy
i
μ
y
ÞÞ.Ify increases as x increases, then the two variables are
187
3.6 Propagation of er ror

positively correlated and have a covariance greater than 0. If y decreases as x
increases, then the two variables are negatively correlated and have a covariance
less than 0.
When adding two random variables x and y such that z
i
¼ C
1
x
i
þ C
2
y
i
, the associated variance is
calculated as
s
2
z
¼ C
2
1
s
2
x
þ C
2
2
s
2
y
þ 2C
1
C
2
s
2
xy
: (3:37)
If x and y are independent random variables, then the values of x have no bearing on
the observed values of y, and it can be easily shown that Eðs
2
xy
Þ¼0 (see the
derivation of Equation (3.27)). In that case,
s
2
z
¼ C
2
1
s
2
x
þ C
2
2
s
2
y
: (3:38)
Often the covariance between two variables is not reported, and one is forced to
assume it is zero when using measured values reported in the literature. Nevertheless,
you should remain aware of the limitations of this assumption.
The mean and varia nce of a result that involv es a subtraction operation between
two random variables can be derived in a similar fashion. If z
i
¼ C
1
x
i
C
2
y
i
, it can
be shown that
z ¼ C
1
x C
2
y (3:39)
and
s
2
z
¼ C
2
1
s
2
x
þ C
2
2
s
2
y
2C
1
C
2
s
2
xy
: (3:40)
This is left to the reader as an exercise.
Estimates of the mean (expected value) and variance of a linear combination
of variables, which are calculated using Equations (3.36)–(3.40), do not require
the assumption of a normal distribution of the variables. However, if the
random variables are all normally distributed and independent, then it can be
shown that their linear combination is also normally distributed with the mean
given by an extension of Equation (3.36) and the variance given by an extension
of Equation (3.38). In other words, if all x
i
for i =1, ..., n are normally
distributed, and
z ¼
X
n
i¼1
C
i
x
i
;
then z is normally distributed with estimated mean and variance, respectively,
z ¼
X
n
i¼1
C
i
x
i
and s
2
z
¼
X
n
i¼1
C
2
i
s
2
i
:
3.6.2 Multiplication/division of random variables
In this section, we calculate the mean and variance associated with the result of a
multiplication or division operation performed on two rand om variables. Let
z
i
¼ x
i
=y
i
. We do not include C
1
and C
2
since they can be factored out as a single
term and then multiplied back for calculating the final result. We write x
i
and y
i
as
x
i
¼
x þ x
0
i
; y
i
¼
y þ y
0
i
;
188
Probability and statistics

where x
0
i
; y
0
i
are the deviations of x and y from their means, respectively. For either of
the variables, the summation of all deviations equals 0 by definition, i.e.
P
n
i¼1
x
0
i
¼ 0;
P
n
i¼1
y
0
i
¼ 0. We assume that x
i
and y
i
are normally distributed and that
the relative errors S
x
=
x; S
y
=
y 1. This implies that x
0
i
; y
0
i
are both small quantities. We
have
z
i
¼
x
i
y
i
¼
x þ x
0
i
y þ y
0
i
¼
x
y
1 þ x
0
i
=
x
1 þ y
0
i
=
yðÞ
:
Expanding 1 þ y
0
i
=
y
1
using the binomial expansion,
z
i
¼
x
y
1 þ
x
0
i
x
1
y
0
i
y
þ
y
0
i
y
2
y
0
i
y
3
þ
!
¼
x
y
1 þ
x
0
i
x
y
0
i
y
þ O
x
0
i
y
0
i
x
y
;
y
0
i
y
2
! !
;
and ignoring the second- and higher-order terms in the expansion, we get
z
i
x
y
1 þ
x
0
i
x
y
0
i
y
: (3:41)
Equation (3.41) expresses z
i
as an arithmetic sum of x
0
i
=
x and y
0
i
=
y, and is used to
derive expressions for
z and s
2
z
:
z ¼
1
n
X
n
i¼1
z
i
1
n
X
n
i¼1
x
y
1 þ
x
0
i
x
y
0
i
y
:
The last two terms in the above equation sum to 0, therefore
z
x
y
: (3:42)
Now, calcul ating the associ ated variance, we obtain
s
2
z
¼
1
n 1
X
n
i¼1
ðz
2
i
z
2
Þ¼
1
n 1
X
n
i¼1
x
y
1 þ
x
0
i
x
y
0
i
y
2
x
y
2
"#
¼
x
y
2
1
n 1
X
n
i¼1
x
0
i
x
2
þ
y
0
i
y
2
þ 2
x
0
i
x
2
y
0
i
y
2
x
0
i
y
0
i
x
y
"#
;
s
2
z
¼
x
y
2
1
x
2
1
n 1
X
n
i¼1
x
0
i
2
þ
1
y
2
1
n 1
X
n
i¼1
y
0
i
2
2
x
y
1
n 1
X
n
i¼1
x
0
i
y
0
i
"#
:
Now,
s
2
x
¼
1
n 1
X
n
i¼1
x
0
i
2
; s
2
y
¼
1
n 1
X
n
i¼1
y
0
i
2
; and s
2
xy
¼
1
n 1
X
n
i¼1
x
0
i
y
0
i
:
When dividing two random variables x and y such that z ¼ x=y, the variance associated with z is given by
s
2
z
¼
x
y
2
s
2
x
x
2
þ
s
2
y
y
2
2
s
2
xy
x
y
"#
: (3:43)
189
3.6 Propagation of er ror

On similar lines one can derive the expressions for
z and s
2
z
when two random
variables are multiplied together.
If z
i
¼ x
i
y
i
and S
x
=
x; S
y
=
y 1, then
z
x
y (3:44)
and
s
2
z
z
2
¼
s
2
x
x
2
þ
s
2
y
y
2
þ 2
s
2
xy
x
y
"#
: (3:45)
The derivation of Equations (3.44) and (3.45) is left to the reader as an exercise.
3.6.3 General functional relationship between two random variables
Let’s now consider the case where z ¼ fx; yðÞ, where f can be any potentially messy
function of x and y. As before, we express x an d y in terms of the mean value
and a deviation, x
i
¼
x þ x
0
i
; y
i
¼
y þ y
0
i
, and fx; yðÞis expanded using the two-
dimensional Taylor series:
fx
i
; y
i
ðÞ¼f
x;
yðÞþx
0
i
df
dx
x;
y
þy
0
i
df
dy
x;
y
þOx
02
i
; y
02
i
; x
0
i
y
0
i
:
Again, we assume that S
x
=
x; S
y
=
y 1, so that we can ignore the second- and
higher-order terms since they are much smaller than the first-order terms. The
mean function value is calculated as follows:
z ¼
1
n
X
n
i¼1
fx
i
; y
i
ðÞ
1
n
X
n
i¼1
f
x;
yðÞþ
df
dx
x;
y
1
n
X
n
i¼1
x
0
i
þ
df
dy
x;
y
X
n
i¼1
y
0
i
f
x;
yðÞ:
(3:46)
The variance associated with fx; yðÞis given by
s
2
z
¼
1
n 1
X
n
i¼1
z
2
i
z
2
1
n 1
X
n
i¼1
f
x;
yðÞþx
0
i
df
dx
x;
y
þy
0
i
df
dy
x;
y
!
2
f
x;
yðÞðÞ
2
2
4
3
5
1
n 1
X
n
i¼1
x
02
i
df
dx
x;
y
!
2
þ y
02
i
df
dy
x;
y
!
2
þ 2x
0
i
y
0
i
df
dx
x;
y
!
df
dy
x;
y
!
2
4
þ2f
x;
yðÞx
0
i
df
dx
x;
y
þy
0
i
df
dy
x;
y
!#
:
On opening the brackets and summing each term individually, the last term is found
to equal 0, so we have
s
2
z
s
2
x
df
dx
x;
y
!
2
þ s
2
y
df
dy
x;
y
!
2
þ 2s
2
xy
df
dx
x;
y
!
df
dy
x;
y
!
: (3:47)
Equation (3.47) is incredibly powerful in obtaining error estimates when combining
multiple random variables and should be committed to memory.
190
Probability and statistics
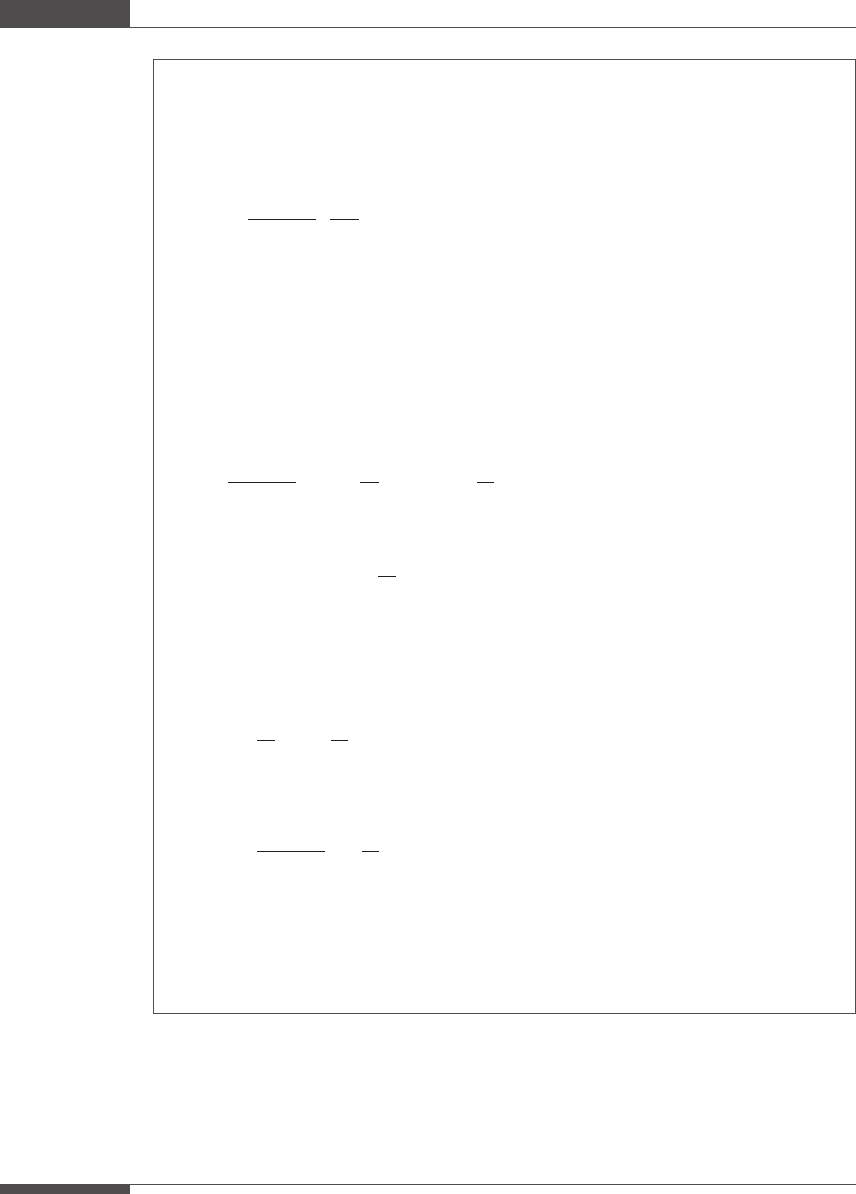
In this section we have derived methods to combine errors in mathematical
expressions containing two random variables. Generalizations for multidimensional
or n-variable systems are discussed in more advanced texts.
3.7 Linear regression error
Hans Reichenbach (1891–1953), a leading philosopher of science and a prominent
educator, stated in The Rise of Scientific Philosophy (Reichenbach, 1951), that
Box 3.8 Sphericity of red blood cells
Red blood cells vary considerably in size even within a single individual. The area (A) and volume (V)of
human red cells have been measured to be 130 ± 15.8 μm
2
and 96 ± 16.1 μm
3
, respectively (Waugh
et al., 1992). Cells can also be characterized by a sphericity S, defined as
S ¼
4π
4π=3ðÞ
2=3
V
2=3
A
:
Using micropipettes, the sphericity of red cells was measured to be 0.78 ± 0.02, after correcting for
minor changes to the area and volume due to temperature changes (Waugh et al., 1992). First, estimate
the variance in sphericity based on the mean values in area and volume, the reported standard
deviations in area and volume, and by neglecting the covariance s
2
VA
between A and V. Next, solve for
s
VA
by keeping the covariance term as an unknown variable and setting your estimate for s
S
equal to the
reported standard deviation of 0.02.
We make use of Equation (3.47) and neglect the covariance term. Calculating the first two terms on
the right-hand side of Equation (3.47), we obtain
4π
4π=3ðÞ
2=3
!
2
s
2
V
df
dV
V;
A
!
2
þ s
2
A
df
dA
V;
A
!
2
2
4
3
5
¼ 23:387 16:1
2
2
3A
V
1=3
V;
A
!
2
þ 15:8
2
V
2=3
A
2
V;
A
2
2
4
3
5
¼ 0:008 þ 0:009 ¼ 0:017;
where f ¼ V
2=3
=A. The estimated variance in the sphericity of red cells s
2
S
neglecting the covariance
between A and V is 0.017. The covariance term has the value
2s
2
VA
df
dV
V;
A
!
df
dA
V;
A
!
¼ 0:02
2
0: 017 ¼0:013:
Evaluating the left-hand side, we obtain
2s
2
VA
4π
4π=3ðÞ
2=3
!
2
2
3A
V
1=3
V;
A
!
V
2=3
A
2
V;
A
¼0:013
or
2s
2
VA
23:387 0:00112 0:00124 ¼0:013;
from which we obtain s
VA
2
= 200.1 μm
5
. (In general, one should not take the square root of the
covariance, since it is not restricted to positive values.)
191
3.7 Linear regression error

A mere report of relations observed in the past cannot be called knowledge; if knowledge is to
reveal objective relations of physical objects, it must include reliable predictions.
The purpose of any regression method is to extract, from a mass of data, information in
the form of a predictive mathematical equation. The sources of scientific and engineer-
ing data include experimental observations obtained in a laboratory or out in the field,
instrument output such as temperature, concentration, pH, voltage, weight, and tensile
strength, or quality control measurements such as purity, yield, shine, and hardness.
Engineering/scientific data sets contain many paired values, i.e. a dependent variable
paired with one or more independent variables. The topic of linear least-squares
regression as a curve-fitting method is discussed extensively in Chapter 2.In
Sections 2.8–2.11, we derived the normal equations, which upon solution yield esti-
mates of the parameters of the linear model, and introduced the residual, SSR (sum of
the squared residuals), and coefficient of determination R
2
. Note that for any mathe-
matical model amenable to linear least-squares regression, linearity of the equation is
with respect to the undetermined parameters only. The equation may have any form of
dependency on the dependent and independent variables. The method of linear regres-
sion involves setting up a mathematical model that is linear in the model parameters to
explain the trends observed in the data. If y depends on the value of x, the independent
variable, then the linear regression equation is set up as follows:
y ¼ β
1
f
1
xðÞþβ
2
f
2
xð Þþþβ
n
f
n
xðÞþE;
where f can be any function of x, and β
1
; β
2
; ...; β
n
are the model parameters. The
individual functions f
i
(x)(1≤ i ≤ n) may depend nonlinearly on x. The dependent
variable y is a random variable that exhibits some varia nce σ
2
about a mean value
μ
y
¼ β
1
f
1
xðÞþβ
2
f
2
xð Þþþβ
n
f
n
xðÞ. The term E represents the random error or
variability associated with y. When the number of data pairs in the data set (x, y)
exceeds the number of unknown parameters in the model, the resulting linear system
of equations is overdetermin ed. As discussed in Chapter 2 , a linear least-squares
curve does not pass through every ( x
i
, y
i
) data point.
The least-squares method is an estimation procedure that uses the limited data at
hand to quantify the parameters of the proposed mathematical model and conse-
quently yield the following predictive model:
^
y ¼ c
1
f
1
xðÞþc
2
f
2
xð Þþþc
n
f
n
xðÞ;
where
^
y are the model predictions of y. The hat symbol (^) indicates that the y values
are generated using model parameters derived from a data set. Our data are subject
to sampling error since the values of the regression-derived model coefficients are
dependent on the data sample. Quantifications of the regression equation coeffi-
cients c
1
; c
2
; ...; c
n
serve as estimates of the true parameters β
1
; β
2
; ...; β
n
of the
model. We use confidence intervals to quantify the uncertainty in using c
1
; c
2
; ...; c
n
as estimates for the actual model parameters β
1
; β
2
; ...; β
n
. Sometimes, one or more
of the c
i
parameters have a physical significance beyond the predictive model, in
which case the confidence interval has an additional importance when reporting its
best-fit value. Before we can proceed further, we must draw your attention to the
basic assumptions made by the linear regression model.
(1) The measur ed values of the independent variable x are known with perfect precision
and do not contain any error.
(2) Every y
i
value is normally distributed about its mean μ
y
i
with an unknown variance
σ
2
. The variance of y is independent of x, and is thus the same for all y
i
.
192
Probability and statistics

(3) The means of the dependent variable y
i
, for the range of x
i
values of interest, obey the
proposed model μ
y
i
¼ β
1
f
1
x
i
ðÞþβ
2
f
2
x
i
ð Þþþβ
n
f
n
x
i
ðÞ.
(4) A y value at any observed x is randomly chosen from the population distribution of y
values for that value of x, so that the random sampling model holds true.
(5) The y measurements observed at different x values are independent of each oth er so
that their covariance σ
2
y
i
y
j
¼ Eððy
i
μ
y
i
Þðy
j
μ
y
j
ÞÞ ¼ 0.
The departure of each y measurement from its corresponding point on the regression
curve is called the residual, r
i
¼ y
i
^
y
i
ðÞ. For the least-squares approximation, it can
be easily shown that the sum of the residuals
P
m
i¼1
r
i
¼
P
m
i¼1
y
i
^
y
i
ðÞ¼0, where m is
the number of data points in the data set.
The residual variance measures the variability of the data points about the regression curve and is
defined as follows:
s
2
y
¼
1
m n
X
m
i¼1
y
i
^
y
i
ðÞ
2
¼
k r k
2
2
m n
; (3:48)
where m is the number of data pairs and n is the number of undetermined model parameters. Note that
k r k
2
2
is the sum of the squared residuals (SSR) (the subscript indicates p = 2 norm).
The degrees of freedom available to estimate the residual variance is given by (m – n).
Since n data pairs are required to fix the n parameter values that define the regression
curve, the number of degrees of freedom is reduced by n when estimating the
variance. If there are exactly n data points, then all n data points are exhausted in
determining the parameter values, and zero degrees of freedom remain to estimate
the variance. When the residual standard deviation s
y
is small, the data points are
closely situated near the fitted curve. A large s
y
indicates considerable scatter about
the curve; s
y
serves as the estimate for the true standard deviation σ of y. Since the
data points are normally distributed vertically about the curve, we expect approx-
imately 68% of the points to be located within ±1SD (standard deviation) from the
curve and about 95% of the points to be situated within ±2SD.
3.7.1 Error in model parameters
Earlier, we present ed five assumptions required for making statistical predictions
using the linear least-squares regression model. We also introduced Equation (3.48),
which can be used to estimate the standard deviation σ of the normally distributed
variable y. W ith these developments in hand, we now proceed to estimate the
uncertainty in the calculated model parameter values.
The equation that is fitted to the data,
y ¼ β
1
f
1
xðÞþβ
2
f
2
xðÞþþβ
n
f
n
xðÞ;
can be rewritten in compact matrix form Ac = y, for m data points, where
A ¼
f
1
x
1
ðÞf
2
x
1
ð Þ f
n
x
1
ðÞ
f
1
x
2
ðÞf
2
x
2
ð Þ f
n
x
2
ðÞ
:
:
:
f
1
x
m
ðÞf
2
x
m
ð Þ f
n
x
m
ðÞ
2
6
6
6
6
6
6
4
3
7
7
7
7
7
7
5
; c ¼
β
1
β
2
:
:
:
β
n
2
6
6
6
6
6
6
4
3
7
7
7
7
7
7
5
; y ¼
y
1
y
2
:
:
:
y
m
2
6
6
6
6
6
6
4
3
7
7
7
7
7
7
5
:
193
3.7 Linear regression error

Box 3.9A Kidney functioning in human leptin metabolism
Typically, enzyme reactions
E þ S ! E þ P
exhibit Michaelis–Menten (“saturation”) kinetics, as described by the following equation:
R ¼
dS
dt
¼
R
max
S
K
m
þ S
:
Here, R is the reaction rate in concentration/time, S is the substrate concentration, R
max
is the maximum
reaction rate for a par ticular enzyme concentration, and K
m
is the Michaelis constant; K
m
can be thought
of as the reactant concentration at which the reaction rate is half of the maximum R
max
. This kinetic
equation can be rearranged into linear form:
1
R
¼
K
m
R
max
1
S
þ
1
R
max
:
Thus, a plot of 1/R vs. 1/S yields a line of slope K
m
=R
max
and intercept 1=R
max
. This is referred to as the
Lineweaver–Burk analysis.
The role of the kidney in human leptin metabolism was studied by Meyer et al.(1997). The data
listed in Table 3.6 were collected for renal leptin uptake in 16 normal post-operative volunteers with
varying degrees of obesity.
In this case the arterial plasma leptin is taken as the substrate concentration S (ng/ml), and the renal
leptin uptake represents the reaction rate R (nmol/min).
We first perform a linear regression on these data using the normal equations to determine the
Michaelis constant and R
max
. The matrices of the equation Ac = y are defined as follows:
Table 3.6.
Subject Arterial plasma leptin
Renal leptin
uptake
1 0.75 0.11
2 1.18 0.204
3 1.47 0.22
4 1.61 0.143
5 1.64 0.35
6 5.26 0.48
7 5.88 0.37
8 6.25 0.48
9 8.33 0.83
10 10.0 1.25
11 11.11 0.56
12 20.0 3.33
13 21.74 2.5
14 25.0 2.0
15 27.77 1.81
16 35.71 1.67
194
Probability and statistics

A ¼
1
S
1
1
1
S
2
1
:
:
:
1
S
16
1
2
6
6
6
6
6
6
6
4
3
7
7
7
7
7
7
7
5
; y ¼
1
R
1
1
R
2
:
:
:
1
R
16
2
6
6
6
6
6
6
6
4
3
7
7
7
7
7
7
7
5
:
The coefficient vector
c ¼
K
m
R
max
1
R
max
"#
¼ A
T
A
1
A
T
y:
Performing this calculation in MATLAB (verify this yourself), we obtain
c
1
¼
K
m
R
max
¼ 6:279; c
2
¼
1
R
max
¼ 0:5774:
Also
SSR ¼k r k
2
2
¼
X
16
i¼1
y
i
^
y
i
ðÞ
2
¼ 12:6551;
where
^
y ¼ 1=
^
R ¼ Ac. The coefficient of determination R
2
= 0.8731, thus the fit is moderately good.
Since m = 16 and n =2,
s
y
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
12:6551
16 2
r
¼ 0:9507:
We assume that the y
i
¼ 1=R
i
values are normally distributed about their mean
^
y
i
with a standard
deviation estimated to be 0.9507. Next, we plot in Figure 3.17 the transformed data, the best-fit model,
and curves that represent the 95% confidence interval for the variability in the y data. Since the residual
standard deviation is estimated with 16 – 2 = 14 degrees of freedom, the 95% confidence interval is
given by
^
y t
0:975; f¼14
s
y
:
Using the MATLAB tinv function, we find that t
0:975; f¼14
¼ 2:145.
We expect the 95% confidence interval to contain 95% of all observations of 1=R for the range of substrate
concentrations considered in this experiment. Out of 16, 15 of the observations are located within the
two dashed lines, or 15=16 ~ 94% of the observations are contained within the 95% confidence region.
Figure 3.17
Plot of the transformed data, the linear least-squares fitted curve (solid line), and the 95% confidence interval for y
(situated within the two dashed lines).
0 0.5 1 1.5
−2
0
2
4
6
8
10
12
1/R (min/nmol)
1/S (ml/ng)
Data points: 1/R
Fitted linear curve
95% confidence interval
195
3.7 Linear regression error

The best-fit least-squares solution c
1
; c
2
; ...; c
n
for the undetermined parameters
β
1
; β
2
; ...; β
n
is given by the normal equations (see Section 2.9) c ¼ A
T
A
1
A
T
y.
Since A is an m × n matrix, A
T
is therefore an n × m matrix, and A
T
A and A
T
A
1
are n × n matr ices. The matrix product A
T
A
1
A
T
produces an n × m
matrix which undergoes matrix-vector multiplication with y,anm × 1 vector. Let
K ¼ A
T
A
1
A
T
. We can then write
c ¼ Ky or c
i
¼
X
m
j¼1
K
ij
y
j
; for 1 i n:
Each coefficient c
i
of the model is equal to a linear combination of m normally
distributed random variables. It follows that c
i
will be normally distributed.
Equation (3.37) guides us on how to combine the variances s
2
y
j
associated with
each random variable y
j
. The second assumption in our list states that the variance
σ
2
is the same for all y. Now, s
2
y
is our estimate for σ
2
,so
s
2
c
i
¼
X
m
j¼1
K
2
ij
s
2
y
j
¼
X
m
j¼1
K
2
ij
s
2
y
: (3:49)
Equation (3.49) is used to estimate the variance or uncertainty associated with the
calculated model coefficients.
3.7.2 Error in model predictions
The utility of regression models lies in their predictive nature. Mathematical models
fitted to data can be used to predict the mean value of y for any given x
0
that lies
within the range of x values for which the model is defined. As noted earlier, an
actual observed value of y varies about its true mean with a variance of σ
2
.A
predicted value of y at x
0
will have a mean
μ
y
0
¼ Eyjx
0
ðÞ¼β
1
f
1
x
0
ðÞþβ
2
f
2
x
0
ð Þþþβ
n
f
n
x
0
ðÞ:
The best prediction we have of the mean of y at x
0
, when no actual observation of y
at x
0
has been made, is
^
y
0
¼ c
1
f
1
x
0
ðÞþc
2
f
2
x
0
ð Þþþc
n
f
n
x
0
ðÞ:
The model prediction of the mean
^
y
0
is not perfect because the estimated regres-
sion model parameters a re themselves associated with a level of uncertainty
quantified by their respective confidence intervals. To convey our confidence in
the prediction of
^
y
0
, we must specify confidence intervals that bracket a range in
which we expect the actual mean of y
0
to lie. Although y at any x is associated with
a variance of σ
2
,
^
y
0
, our prediction of the mean at x = x
0
, will be associated
with an error t hat will depend on the uncertainty in the model coefficients. Let’s
now calculate the variance in the predicted value
^
y
0
, which serves as our estimate
ofthetruemeanμ
y
0
.
Suppose the linear regression model is
^
y ¼ c
1
f
1
xðÞþc
2
f
2
xðÞ. Using Equat ion
(3.37), we calculate the variance associated with
^
y
0
as
s
2
^
y
0
¼ f
1
x
0
ðÞðÞ
2
s
2
c
1
þ f
2
x
0
ðÞðÞ
2
s
2
c
2
þ 2f
1
x
0
ðÞf
2
x
0
ðÞs
2
c
1
c
2
:
The covariance term cannot be dropped because s
2
c
1
c
2
6¼ 0. We must determine the
covariance in order to proceed. We have
196
Probability and statistics
