King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

carefully designed to prevent poten tial confounders such as sociodemographic

factors, gender, diet, and substance abuse from inﬂuencing the result. One can use

simple standardization procedures to adjust the population parameter estimate to

correspond to the same distribution of the confounding variable(s) in all study

samples. Alternatively, special experimental designs are employed called restricted

randomization techniques. Blocking is one method of restricted randomization in

which the study group is divided into blocks. Each block contains the same number

of experimental subjects. Randomized allotment of subjects to each treatment group

is performed within each block. A key feature of the blocking method is that, within

each block, variation among subjects due to effects of extraneous variables except

for the treatment differences is minimized. Extraneous variability is allowed between

the blocks. Stratiﬁcation is an other method of restricted randomization in which the

treatment or observed groups are divided into a number of categor ies (strata) that

are deﬁned by the control variable. Individuals are then randomly allocated to the

treatment groups within each strata.

Randomization is part and parcel of every experimental design. It minimizes

biases in the result, many of which are unknown to the experimentalist. Blocking

methods or stratiﬁcation designs help to improve the precision of the experiment.

These methods are different from the completely randomized design discussed earlier,

in which the study group is not divided into strata or blocks. This is the only

experimental design considered in this book. Other experimenta l designs require

more sophisticated techniques of analysis which are beyond the scope of this book.

There are many options available for designing an experiment, but the choice of the

best design method depends upon the nature of the data and the experimental

procedures involved. The design of experiments is a separate subject in its own

right, and is closely linked to the ﬁeld of statistics and probability.

In this section, we have distinguished between two broadly different methods of

scientiﬁc study – experimental and observational – used to test a hyp othesis.

Henceforth, we refer to all scientiﬁc or engineering studies that are performed to

generate data for hypothesis testing as “experiments.” We will qualify an “experi-

ment” as an experimental or observational study, as necessary.

4.2.2 Null and alternate hypotheses

Before conducting a scientiﬁc study (or engineering analysis that involves hypothesis

testing), the original hypothesis should be reconstructed as two complementary

hypotheses. A hypothesis cannot be proven or deemed as “true,” no matter how

compelling the evidence is. There is no absolute guarantee that one will not ﬁnd

evidence in the future that contradicts the validity of the hypothesis. Therefore, instead

of attempting to prove a hypothesis, we use experimental data as evidence in hand to

disprove a hypothesis. If the data provide evidence contrary to the statement made by

the hypothesis, then we say that “the data are not compatible with the hypothesis.”

Let’s assume we wish to test the following hypothesis:

“People with type-2 diabetes have a blood pressure that is different from that of healthy

people.”

In order to test our hypothesis, a sample must be selected from the adult pop-

ulation diagnosed with type-2 diabetes, and blood pressure readings from each

individual in the group must be obtained. The mean blood pressure values of this

217

4.2 Formulating a hypothesis

sample are compared with the population mean blood pressure of the non-diabetic

fraction of the adult population. The exact method of comparison will depend upon

the statistica l test chosen.

We also rewrite our original hypothesis in terms of two contradicting statements.

The ﬁrst statement is called the null hypothesis and is denoted by H

“People with type-2 diabetes have the same blood pressure as healthy people.”

This statement is the opposite of what we suspect. It is this statement that is tested

and will be either retained or rejected based on the evidence obtained from the study.

Due to inherent sampling error, we do not expect the differences between the two

populations to be exactly zero even if H

is true. Some difference in the mean blood

pressures of the samples derived from both populations will be observed irrespective

of whether H

is true or not. We want to know whether the observed dissimilarity

between the two samples is due to natural sampling varia tion or due to an existing

difference in the blood pressure characteristics of the two populations. Hypothesis

testing searches for this answer. A statistical test assumes that the null hypothesis is

true. The magnitude of deviation of the sample mean (mean sample blood pressure

of type-2 diabetics) from the expecte d value under the null hypothesis (mean blood

pressure of healthy individuals) is calculated. The extent of deviation provides clues

as to whether the null hypothesis should be retained or rejected.

We also formulate a second statement:

“People with type-2 diabetes have a blood pressure that is different from that of healthy

people.”

This statement is the same as the original research hypothesis, and is called the

alternate hypothesis. It is designated by H

. Note that H

and H

are mutually

exclusive events and together exhaust all possible outcomes of the conclusion.

If the blood pressure readings are similar in both populations, then the data will

not appear incompatible with H

. We say that “we fail to reject the null hypothesis”

or that “there is insufﬁcient evidence to reject H

.” This does not mean that we accept

the null hypothesis. We do not say that “the evidence supports H

.” It is possible that

the data may support the alternate hypothesis. Perhaps the evidence is insufﬁcient,

thereby yielding a false negative, and availability of more data may establish a

signiﬁcant difference between the two samples and thereby a rejection of H

. Thus,

we do not know for sure which hypothesis the evidence supports. Remember, while

our data cannot prove a hypothesis, the data can contradict a hypothesis.

If the data are not compatible with H

as inferred from the statistical analysis,

then we reject H

. The criterion for rejection of H

is determined before the study is

performed and is discussed in Section 4.3. Rej ection of H

automatically means that

the data are viewed in favor of H

since the two hypotheses are complementary.

Note that we do not accept H

, i.e. we cannot say that H

is true. There is still a

possibility that H

is true and that we have obtained a false positive. However, a

“signiﬁcant result,” i.e. one that supports H

, will warrant further investigation for

purposes of conﬁrmation. If H

appears to be true, subsequent action may need to

be taken based on the scientiﬁc signiﬁcance (as opposed to the statistical signiﬁcance)

of the result.

On the other hand, the statement posed by the null hypothesis is

A statistically signiﬁcant result implies that the populations are different with respect to a population

parameter. But the magnitude of the difference may not be biologically (i.e. scientiﬁcally) signiﬁcant.

For example, the statistical test may provide an interval estimate of the difference in blood pressure of

218

Hypothesis testing

one that usually indicates no change, or a situation of status quo. If the null

hypothesis is not rejected, in most cases (except when the null hypothesis does not

represent status quo; see Section 4.6.1 for the paired sample t test) no action needs to

be taken.

Why do we test the null hypothesis rather than the alternate hypothesis? Or, why

do we assume that the null hypothesis is true and then proceed to determine how

incompatible the data is with H

? Why not test the alternate hypothesis? If instead,

we assume that H

is false, then H

must be true. Now, H

always includes the sign

of equality between two or more populations with respect to some property or

population variable. Accordingly, H

does not represent equality between two

population parameters. If we assume H

to be true, then we do not know a priori

the magnitude of difference between the two populations with respec t to a particular

property. In that case, it is not possible to determine how incompatible the data are

with H

. Therefore, we must begin with the equality assumption.

4.3 Testing a hypothesis

The procedure of testing a hypothesis involves the calculation of a test statistic.

A test statistic is calculated after a hypothesis has been formulated, an experiment

has been designed to test the null hypothesis, and data from the experiment have

been collected. In this chapter, we are primarily concerned with formulating and

testing hypotheses concerning the population mean or median. The method chosen

to calculate the test statistic depends on the choice of the hypothesis test. The value

of the test statistic is determined by the extent of deviation of the data (e.g. sample

mean) from expected values (e.g. expected population mean) under the null hypoth-

esis. For illustrative pur poses, we discuss the one-sample z test.

Assume that we have a random sample of n = 100 men of ages 30 to 55 that have

disease X. This sample is representative of the popul ation of all men between ages

30 and 55 with disease X. The heart rate within population X is normally distributed.

The sample statistics include mean

x and sample variance s

. Because the sample

is fairly large, we assume that the population variance σ

is equal to the sample

variance.

We wish to know if population X has a heart rate similar to that of the population

that does not have disease X. We call the latter population Y. The heart rate at rest in

the adult male Y population is normally distributed with mean μ

and variance σ

which is the same as the variance of population X.

The non-directional null hypothesis H

“The heart rate of the X population is the same as that of the Y population.”

If the mean heart rate of population X is μ, then H

can be stated mathematically

as H

: μ = μ

The non-directional alternate hypothesis H

“The heart rate of the X population is different from that of the Y population,”

or H

: μ ≠ μ

type-2 diabetics from that of the healthy population as 0.5–1 mm Hg. The magnitude of this difference

may not be important in terms of medical treatment and may have little, if any, biological importance. A

statistically signiﬁcant result simply tells us that the difference observed is attributable to an actual

difference and not caused by sampling error.

219

4.3 Testing a hypothesis

4.3.1 The p value and assessing statistical significance

We want to know if population X is equivalent to population Y in terms of heart

rate. In Chapter 3, we discussed that the means

x of samples of size n taken from a

normal population (e.g. population Y) will be distributed normally N μ

; σ=

ﬃﬃﬃ

ðÞ

with population mean μ

and variance equal to σ

=n. If the null hypothesis is true,

then we expect the means of samples (n = 100) taken from population X to be

normally distributed with the population mean μ

and variance σ

=n.

We can construct an interval from the population Y mean

 z

1α=2

ﬃﬃﬃ

using the population parameters such that 100(1 – α)% of the samples of size n drawn

from the refer ence population will have a mean that falls within this range. If the

single sample mean we have at our disposal lies within this range, we conclude that

the mean of the sample drawn from population X is not different from the popula-

tion Y mean. We do not reject the null hypothesis. If the sample mean lies outside the

conﬁdence interval constructed using population Y parameters, then the mean of the

population X from which the sample is derived is considered to be different from the

mean of population Y. This result favors the alternate hypothesis.

Alternatively, we can calculate the z statistic,

z ¼

x  μ

σ=

ﬃﬃﬃ

; (4:1)

which is the standardized deviation of the sample mean from the population mean

if H

is true. The z statistic is an example of a test statistic. The magnitude of the z

statistic depends on the difference between the sample mean and the expected value

under the null hypothesis. This difference is normalized by the standard error of the

mean. If the difference between the observed and expected values of the sample mean

is large compared to the variability of the sample mean, then the likelihood that this

difference can be explained by sampling error is small. In this case, the data do not

appear compatible with H

. On the other hand, if the difference is small, i.e. the value

of z is close to zero, then the data appear compatible with H

Every test statistic exhibits a speciﬁc probability distribution under the null

hypothesis. When H

is true, the z statistic is distributed as N(0, 1). For any value

of a test statist ic, we can calculate a probability that tell s us how common or rare this

value is if the null hypothesis is true. This probability value is called the p value.

The p value is the probability of obtaining a test statistic value at least as extreme as the observed value,

under the assumption that the null hypothesis is true. The p value describes the extent of compatibility

of the data with the null hypothesis. A p value of 1 implies perfect compatibility of the data with H

In the example above, if H

is true, we expect to see a small difference between the

sample mean and its expected value μ

most of the time. A small deviation of the

sample mean

x from the expected population mean μ

yields a small z statistic, which

is associated with a large p value. Small deviations of the sample mean from

the expected mean can easily be explained by sampling differences. A large p value

demonstrates compatibility of the data with H

. On the other hand, a very small

p value is associated with a large difference between the mean value of the sample

220

Hypothesis testing

data and the value expected under the null hypothesis. A small p value implies that

when the null hypothesis is true, the chance of observing such a large difference is

rare. Large discrepancies between the data and the expected values under the null

hypothesis are more easily explained by a real difference between the two populations

than by sampling error, and therefore suggest incompatibility of the data with H

A cut-off p value must be chosen that clearly delineates test results co mpatible

with H

from those not compatible with H

The criterion for rejection of the null hypothesis is a threshold p value called α, the significance level.

The null hypothesis is rejected when p ≤ α.

For the z test, α corresponds to the area under the standard normal curve that is

associated with the most extreme values of the z statistic. For other hy pothesis tests,

the test statistic may not have a standard normal distribution, but may assume some

other probab ility distribution.

The significance level α is the area under the probability distribution curve of the test statistic that

constitutes the rejection region.Ifap value less than α is encountered, then the discrepancy between

the test statistic and its expected value under the null hypothesis is interpreted to be large enough to

signify a true difference between the populations. The test result is said to be “statistically signifi-

cant” and the populations are said to be “significantly different at the α level of significance.”

A statistically signiﬁcant result leads to rejection of H

. The (1 – α) area under the

distribution curve represents the region that does not lead to rejection of H

.Ifp > α,

then the test result is said to be “statistically insigniﬁcant.” The data do not provide

sufﬁcient evidence to reject H

. This explains why hypothesis tests are also called

tests of signiﬁcance. For purposes of objectivity in concluding the statistical signiﬁ-

cance of a test, the signiﬁcance level is set at the time of experimental design before

performing the experiment.

So far we have alluded to non-directional or two-sided hypotheses, in which a

speciﬁc direction of the difference is not investigated in the alternate hypothesis.

A non-directional hypothesis is formulated either when a difference is not expected

to occur in any particular direction, or when the direction of difference is immaterial

to the experimenter. A non-directional hypothesis can be contrasted with a direc-

tional hypothesis, discussed later in this section. In a non-directional hypothesis test,

only the magnitude and not the sign of the test statistic is important for assessing data

compatibility with H

. For a non-directional z test, if the signiﬁcance level is α, then the

rejection region is equally distributed at both ends (tails) of the standard normal curve

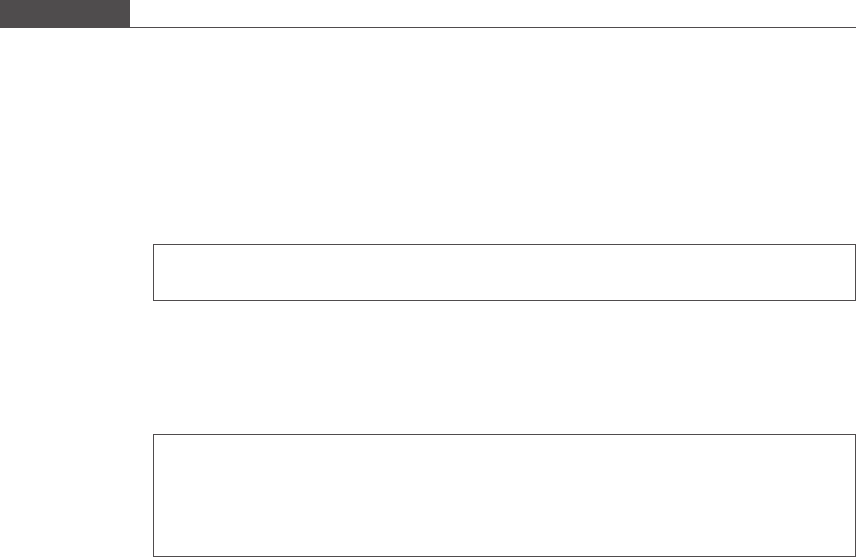
as shown in Figure 4.1. Hence, a non-directional z test is also called a two-tailed test.

Each tail that contributes to the rejection region has an area of α/2 (see Figure 4.1). If

α = 0.05, then 2.5% of the leftmost area and 2.5% of the rightmost area under the

curve (tail regions) together form the rejection region. The critical values of z that

demarcate the rejection regions are z

α=2

and z

1α=2

such that

Φ z

α=2



¼ α=2 and Φ z

1α=2



¼ 1 α=2;

where Φ is the cumulative distribution function for the normal distribution (see

Section 3.5.4, Equation (3.34)). If the calculated z value falls in either tail region, i.e.

z < z

α=2

or z > z

1α=2

, then the result is statistica lly signiﬁcant and H

is rejected (see

Figure 4.1).

221

4.3 Testing a hypothesis

How is the p value calculated for a two-sided z test? If z < 0, then the probability

of obtaining a value of the test statistic at least as extreme as what is observed is

p ¼ Φ zðÞ, when considering only negative values of z. For a non-directional hypo-

thesis test, large positive or negative values of z can lead to rejection of H

. It is the

absolute value of z that is important. When calculating the p value, we must also take

into account the probability of observing positive z values that are at least as extreme

as the observed absolute value of z. When z < 0, the p value is calculated as

p ¼ Φ zðÞþ1 Φ z

ðÞ:

Since the z distribution is perfectly symmetric about 0, Φ zðÞ¼1Φ z

ðÞfor z <0.

Then,

p ¼ 2Φ zðÞ:

If z > 0, then

p ¼ 21 Φ zðÞðÞ:

We can condense the above equations into a single equation by using the absolute

value of z.

For a two-sided z test, p is calculated as

p ¼ 21 Φ zjjðÞðÞ: (4:2)

There are two routes one can take to determine if the test result is statistically

signiﬁcant.

(1) Using the p value. The p value associated with the calculated test statistic is com-

pared with the signiﬁcance level of the test, α.

(a) If p < α, H

is rejected.

(b) If p > α, H

is retained.

(2) Using the test statistic. The calcul ated test statistic is compared with the critical

value. In the z test, z is compared with the threshold value of z, which is z

1α=2

(a) If z

1α=2

, H

is rejected.

(b) If z

1α=2

, H

is retained.

Figure 4.1

Two-sided z test; z follows the N(0,1) distribution curve when H

is true. The shaded areas are the rejection regions.

α/2

– α)

α/2

1–α/2

N(0,1) distribution of z

under H

Rejection region Rejection region

222

Hypothesis testing

The p value method is preferred for the reason that the p value precisely conveys

how strong the evidence is against H

. A very small p value < 0.001 usually indicates

a highly signiﬁcant result, while p ∼ 0.05 may indicate a result that is barely

signiﬁcant. Reporting the p value in addition to stating whether your results

are signiﬁcant at the α level is good practice. Other professionals in the same or

related ﬁelds who use and interpret your data will have the freedom to set their own

criteria for the signi ﬁcance level and decide for themselves the signiﬁcance of the

result.

The alternate hypothesis can also be directional or one-sided. Sometimes, a differ-

ence between two populations is expected to occur in only one direction. For

example, 15-year-old children are expected to be taller than 10-year-old children.

Administering an analgesic is expected to lower the pain and not increase it. In these

cases, it is natural to formulate the alternate hypothesis in a single direction:

: “On average, a 15-year-old girl is taller than a 10-year-old girl.”

: “Treatment with analgesic A will alleviate pain.”

If analgesic A does happen to increase the pain, the result is insigniﬁcant to us.

The drug will be worthless if it does not reduce the pain. In this case, we are interested

in a diff erence in a single direction, even if a difference may occur in either direction.

When the alternate hypothesis is one-sided , H

must include either a greater than

or less than sign (depending on the direction of H

) in addition to the equality. The

null hypotheses that complement the alternate hypotheses stated above are:

: “On average, a 15-year-old girl is the same height or shorter than a 10-year-old

girl.”

: “Treatment with analgesic A will either not change the amount of pain or

increase it.”

When the hypothesis is one-sided, we look for statistica l signiﬁcance in only

one direction – the direction that coincides with the alternate hypothesis. In a

one-sided test, the 100α% of the most extreme outcomes that qualify rejec tion of

are conﬁned to one side of the probability distribution curve of the test statistic.

In other words, the rejection region is located either on the left or the right side

of the null distribution, but not on both. On the other hand, test values that

fall on the opposite side of the rejection region reinforce the null hypothesis.

The procedure to evaluate a one-sided hypothesis test is demonstrated for the z

test. The two-sided hypothesis on heart rate in populations X and Y presented

earlier is converted to a single-sided hypothesis. The one-sided alternate hypothesis

is:

“The heart rate of population X is greater than the heart rate of population Y.”

is mathematically writt en as H

: μ > μ

The null hypothesis H

is:

“The heart rate of population X is either less than or equal to the heart rate of population Y.”

can be stated mathematically as H

: μ ≤ μ

Note that while the null hypothesis statement contains the condition of equality, it

also includes inﬁnite other possibilities of μ < μ

. However, rejection of H

: μ = μ

spawns automatic rejec tion of H

: μ < μ

. You can demonstrate this yourself. We

only need to check for incompatibility of the data with H

: μ = μ

. For this reason,

223

4.3 Testing a hypothesis

the z statistic for a one-sided hypothesis is calculated in the same way as for a non-

directional hypothesis:

z ¼



x  μ

σ=n

Large positive values of z will lead to rejection of the null hypothesis. On the other

hand, small or large negative values of z will not cause rejec tion. In fact, for z ≤ 0, the

null hypothesis is automatically retained, because the direction of the difference is

the opposite of that stated in the alternate hypothesis and p > 0.5. Only when z >0

does it become necessary to determine if the value of the test statistic is signiﬁcant.

The p value associated with the z statistic is the probability that if H

is true, one will

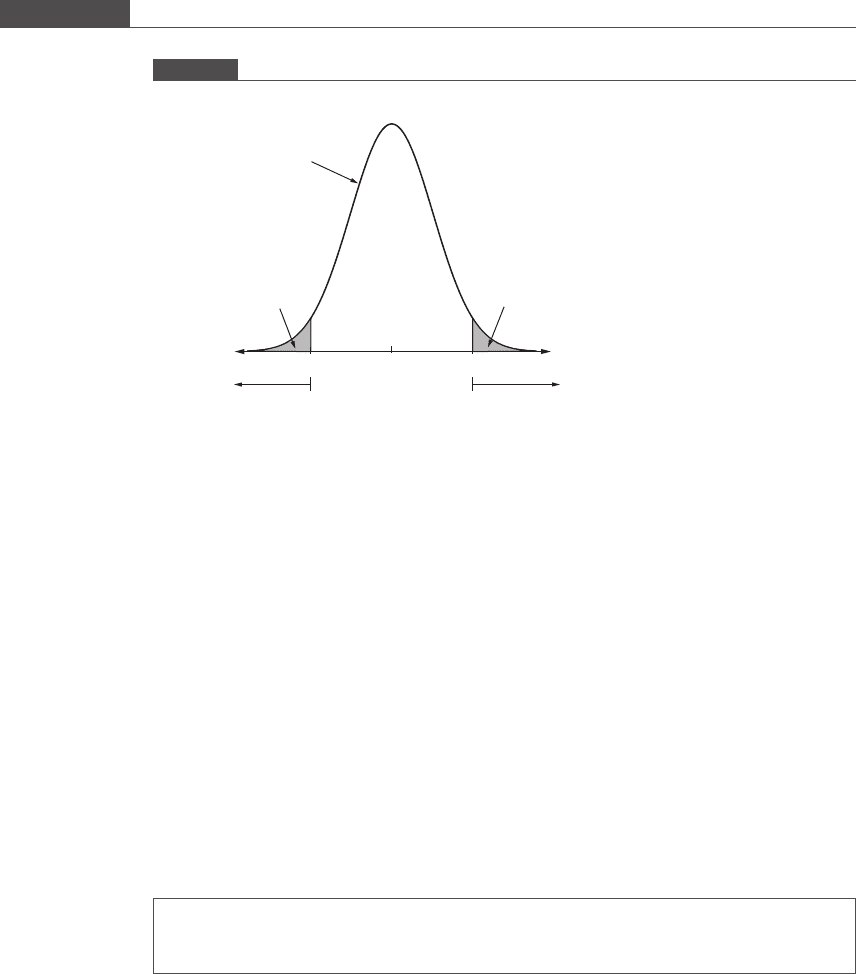
obtain a value of z equal to or greater than the observed value. If α is the signiﬁcance

level, the rightmost area under the curve equal to α forms the rejection region, as

shown in Figure 4.2.

The critical value of z that deﬁnes the lower bound of the rejection region, i.e. z

1α

satisﬁes the criterion

1 Φ z

1α

ðÞ¼α:

If α = 0.05, then z

1α

¼ 1:645:

A one-sided alternate hypothesis may express negative directionality, i.e.

: μ

Then, the null hypothesis is formulated as H

: μ ≥ μ

For this case, large negative values of z will lead to rejection of the null hypothesis,

and small or large positive values of z will not cause rejection. If z ≥ 0, the null

hypothesis is automa tically retained. One needs to look for statistical signiﬁcance

only if z < 0. The p value associated with the z statistic is the probability that if H

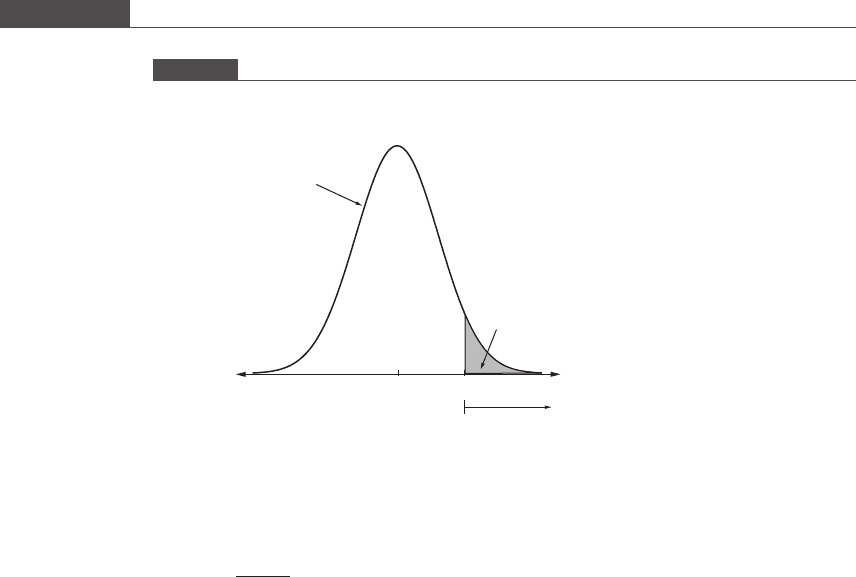
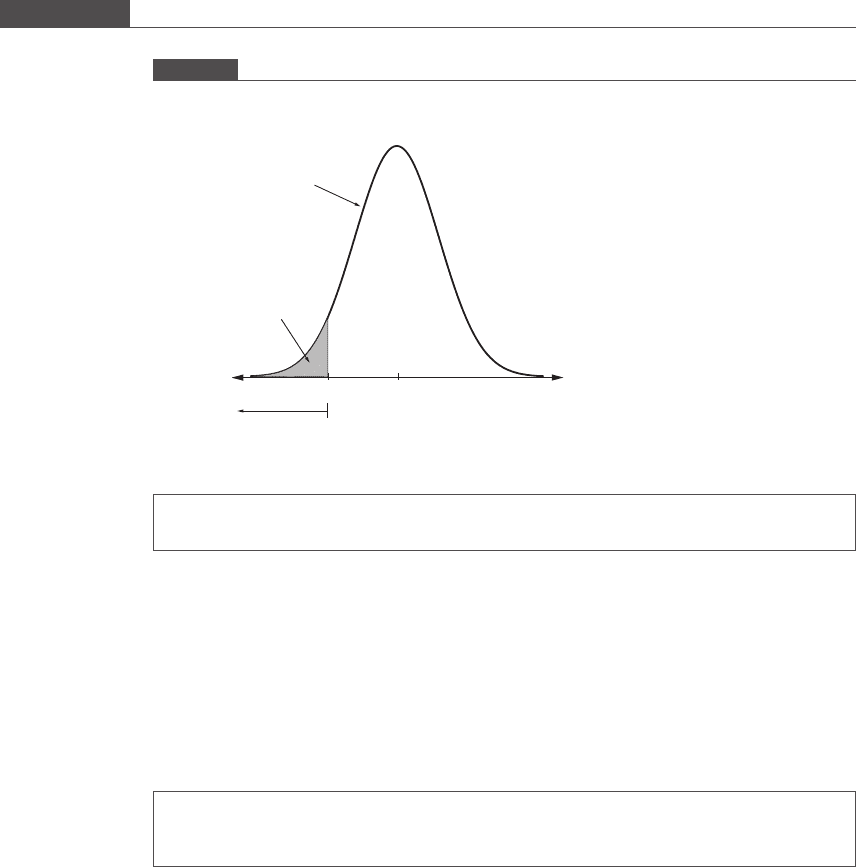
true, one will obtain a value of z equal to or less than the observed value. If α is the

signiﬁcance level, the leftmost area under the curve equal to α forms the rejection

region, as shown in Figure 4.3. The deﬁnition of the p value can be generalized for

any one-sided hypothesis test.

Figure 4.2

One-sided z test for an alternate hypothesis with positive directionality. The shaded area located in the right tail is the

rejection region.

(1 – α)

0 z

1–α

N(0,1) distribution of z

under H

Rejection re

ion

224

Hypothesis testing

The p value of a directional hypothesis test is the probability, if H

is true, of obtaining a test statistic

value at least as extreme as the observed value, measured in the direction of H

The critical value of z that deﬁnes the upper bound of the rejection region, i.e. z

satisﬁes the criterion

Φ z

ðÞ¼α:

If α = 0.05, then z

¼1:645:

Irrespective of the direction of the alternate hypothesis, the p value for a one-sided

z test can be calculated using Equation (4.3) presented below.

For a one-sided z test, p is calculated as

p ¼ 1 Φ zjj

ðÞðÞ

: (4:3)

Upon comparing Equations (4.2) and (4.3), you will notice that for the same value

of z, the p value differs by a factor of 2 depending on whether the hypothesis is

directional. This has serious implications. The p value of a directional hypothesis

will be less (half for symm etrically distributed null distributions) than that for a

non-directional statement. Some researchers convert a non-signiﬁcant result to a

signiﬁcant result simply by switching the nature of the hypothesis from one of no

directionality to a directional one. This constitutes bad science. The choice between a

directional and non-directional hypothesis should be made before collecting and

inspecting the data. If a directional hypothesis is chosen, the direction should be

guided by logical and scientiﬁc implications. If we formulate a directional hypothesis

after surveying the data, we might be tempted to choose a direction that facilitates

rejection of H

. This is da ngerous, since the probability of making a type I error

(false positive) doubles when we perform an unwarranted directional analysis. If, in

reality, the null hypothesis is correct, subsequent studies are likely to yield contra-

dictory results, undermining your conclusions. When in doubt, you should employ a

Figure 4.3

One-sided z test for an alternate hypothesis with negative directionality. The shaded area located in the left tail is the

rejection region.

(1 – α)

0 zz

N(0,1) distribution of z

under H

Rejection re

ion

225

4.3 Testing a hypothesis

two-sided test, which, although more conservative than a one-sided test, cannot be

called into question.

As discussed earlier for the two-sided test, you can use either of the following

methods to assess statistical signiﬁcance when performing a one-sided hypothesis

test.

(1) Using the p value. The p value associated with the calculated test statistic is com-

pared with the signiﬁcance level of the test, α.

(a) If p < α, H

is rejected.

(b) If p > α, H

is retained.

(2) Using the test statistic. The calcul ated test statistic is compared with the critical

value. In the z test, z is compared with the threshold value of z that deﬁnes the

rejection region.

(a) When testing for positive directionality

(i) if z

1α

, H

is rejected;

(ii) if z

1α

, H

is retained.

(b) When testing for negative directionality

(i) if z

, H

is rejected;

(ii) if z

, H

is retained.

The p values that correspond to various possible values of a test statistic are

published in tabular format in many standard statistics textbooks, and also on

the Internet, for a variety of statistical tests (e.g. z test, t test, F test, and χ

test). A

p value can also be calculated using statistical functions offered by software that

perform statistical analysis of data, such as Minitab, SAS, and Statistics Toolbox in

MATLAB. In this chapter, you will be introduced to a variety of Statistics Toolbox

functions that perform tests of signiﬁcance.

4.3.2 Type I and type II errors

If the value of the test statistic lies in the rejection region as deﬁned by α, we naturally

conclude the test result to be signiﬁcant and reject the null hypothesis. However,

it may be possible that the observed differences in the populations are due to

sampling variability and no actual difference exists. Our choice of α (made prior to

the calculation of the test statistic) is the probability that if the null hypothesis is

true, we will still reject it. In other words , if we were to repeat the study many times,

and if the null hypothesis were true, we would end up rejecting the null hypothesis

(and thereby make an error) 100α% of the time. Thus, when we choose a signiﬁcance

level α, we are, in fact, deciding the probability that, when the null hypothesis is

true, we will commit a false positive error.

Rejection of the null hypothesis H

, when H

is actually true, constitutes a type I error or a false

positive. The probability of making a type I error, when H

is true, is the significance level α.

When we reject the null hypothesis, there is always the possibi lity that we are

making a type I error. We want to minimize the risk of incorrectly rejecting H

, and

therefore we choose a small value for α. A signiﬁcance level of 5%, or α = 0.05, is

widely used in most studies since it usually affords acceptable security against a type

I error. In certain situations, one must choose a more conservative value of α, such

as 0.01 or 0.001.

226

Hypothesis testing