King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

If the test result is not signiﬁcant, we fail to reject the null hypothesis. There is a

chance that a difference between the populations truly exists, but this may not be

evident from the data. Or perhaps the chosen signiﬁcance level is so small that

even large differences between the samp les yiel d an insi gniﬁcant test statistic

value. If the null hypothesis is actually f alse, but our test result is not statistically

signiﬁcant, we have a false negative result. Table 4.2 identiﬁes all possible test

result scenarios.

When we do not reject a false null hypothesis, we make a type II error. If the null hypothesis is false, the

probability of making a type II error is β. In other words, β is the probability of obtaining a statistically

insignificant result, even when the null hypothesis is incorrect.

If β is the probability of failing to reject a false null hypothesis, then (1 – β) is the

probability of rejecting a false null hypothesis, thereby taking the correct action

when the alternate hypothesis is true.

The power of the hypothesis test is given by (1 – β). It is the probability of rejecting a false null

hypothesis.

When rejecting the null hypothesis, one only has to worr y about making a type I

error. Similarly, when failing to reject the null hypothesis, one only needs to consider

the risk of making a type II error. Of course, you will not know if your conclusion is

correct or wrong. You cannot calculate the probability of having made the right

decision. For example, the statement “There is an 80% chance that the null hypoth-

esis is true” is illogical. Such calculations are not possible. The null hypothesis is

either 100% true or 100% false. Thus, when you reject, or fail to reject, the null

hypothesis, you are either right or wrong. But, provided you know α and β, you will

at least be cognizant of the chances of committing an error when the null hypothesis

is true, or when it is false.

Since α is a parameter that you ﬁx before you conduct the hypothesis test, you

have the ab ility to exert control over the risk of making a type I error. However, you

will not know β at the outset unless you estimate it. The power β depends on many

factors, such as sample size, variance of the null distribution

,andα. If the null

hypothesis is not rejected, and the risk of making a type II error is unknown, the

decision to retain H

will not hold much weight. For example, if β ¼ 0:7, and H

false, there is a 30% chance that we will obtain a test result that correctly identiﬁes

Table 4.2. Conditions under which type I and type II errors are made

Test result

Test result is

insigniﬁcant → H

retained

Test result is

signiﬁcant → H

rejected

is True correct type I error (false positive)

is True type II error (false negative) correct

The null distribution is the probability (or sampling) distribution of the test statistic under the assump-

tion that the null hypothesis is true.

227

4.3 Testing a hypothesis

this and leads us to reject H

. In such situations, we will end up failing to reject the

null hypothesis most of the time regardless of what is true. Since the value of α

strongly impacts the power of a test, α must be chosen carefully. If α is very small, say

α = 0.001, then the probability that we will not reject the null hypothesis even if it is

false is greatly increased. As we increase α (make the test less conservative), the

chance of rejecting the null hypothesis in favor of the alternate hypothesis increases.

An optimal value of α should be appropriately chosen to control both type I and

type II errors. In many cases, a signiﬁcance level of 0.05 affords sufﬁciently small

probability of a type I error, but isn’t so small that the power of the test is

unnecessarily compromised.

Because β is often large and uncontrolled, there is substantial risk of making a

type II error when the null hypothesis is not rejected. This explains why we avoid

the terminology “accepting the null hypothesis” and instead use “fail to reject,” even

when we have compelling evidence at our disposal supporting the null hypothesis.

Undoubtedly then, estimation of β is very useful, and it substantiates the credibility

of our assertion that the data favor the null hypothesis. For many tests, α is chosen

as 0.05 (or less ) and β > α. Often, one ﬁnds a β value of 0.2 or a power of 80%

acceptable. In Section 4.5, we show how to calculate the power of a z test.

The decision of choosing suitable values for α and β rests on the consequences of

making a type I and a type II error, respectively. For example, if mu ch is at stake

when a type II error is made (e.g. testing for dangerous side-effects of a new drug), it

is critical to design the experiment so that β is as small as possible.

Remember that null hypotheses are often statements of status quo, and, if true, no

action needs to be taken. The alternate hypotheses are the action-packed statements

that suggest a change be mad e. Any action that is suggested must be backed up with

compelling proof, i.e. a hypothesis test that yields a convincing result. Therefore, the

risk of a type I error should be kept small so that we are conﬁdent of our decision

when we reject H

Example 4.1

Intake of a food type X in a person’ s diet is believed to reduce premature hair loss for those who are

predisposed to this condition. A researcher hypothesizes the following:

: “X does not reduce premature hair loss.”

: “X reduces premature hair loss.”

If the data reveal that X decelerates premature hair loss, when actually there is no effect of X, then

the researcher has made a type I error. If this result is published, unnecessary hype and hope will be

generated with the public. People afflicted with this condition, or even others who do not have this problem,

may alter their diets to incorporate X. Depending on the nutritive value of X, moderate or excessive amounts

of intake of X may be unhealthy or may predispose those consuming X to other conditions, such as

metabolic disorders, cardiovascular disease, or kidney disease. On the other hand, if the data do not show

any effect of X, when in fact X does alleviate premature hair loss, a type II error has been committed. The

usefulness of X will be dismissed and may be reconsidered only when additional tests are performed to

demonstrate H

. Note that the outcome of making a type I error is much different than a type II error. Which

type of error do you think is more dangerous in this case?

4.3.3 Types of variables

It is importa nt to recognize the characteristics of the variables whose values

are collected in an experiment. For e xample, arithmetic manip ulations can be

228

Hypothesis testing

done on variables that represent speed, weight, age, energy units, le ngth, pressure,

temperature, and altitude. We are subject to greater restrictions if we wish to

process numerically a variable that represents hair color, eye color, gender,

or geographic location. The type of hypothesis test that can be applied to make

statistical inferences depends on th e nature of the random variable(s) measured in

the experiment.

Variables can be broadly classiﬁed into three categories based on the type of

measurement scale used.

(1) Cardinal variables Cardinal variables are numeric measurements that are of either

continuous or discrete nature. These variables follow one of two measurement scales.

(a) Ratio scale According to this scale, the number 0 means absence of the quantity

being measured. Examples include age, weight, length, pressure, charge, current,

speed, and viscosity. The zero point of a ratio scale is immutable. A ratio of two

numbers on this scale indicates the proportionality between the two quantities.

If box A weighs 40 kg, box B weighs 20 kg and box C weighs 10 kg, then box A is

twice as heavy as box B, and box A is four times heavier than box C. Naturally

then, box B is twice as heavy as box C. Even if we convert the measurement scale

from kilograms to pounds, we would ﬁnd the proportionality to be exactly the

same. M easurements of intervals and ratios on this scale provide meaningful

information.

(b) Interval scale The zero position on this scale doe s not mean absence of the

quantity being measured. As a result, ratios of numbers have little meaning on

this scale. Examples include the Fahrenheit scale and Celsius scale for measuring

temperature, in which the zero point is arbitrary and has different meaning for

each scale.

(2) Ordinal variables Variables of this type are numbers specifying categories that can

be ranked in a particular order. For example, a child’s mastery of a skill may be

ranked as: not developed, in progress, or accomplished. Each skill category is given a

number such that a higher number indicates greater progress. More examples of

ordinal variables include movie ratings, ranking of items according to preference,

ranking of children in a class according to height or test scores , ranking of pain on a

scale of 1 to 10, and Apgar scores ranging from 0 to 10 assigned to indicate the health

of a baby at the time of birth. There is no unifor mity in the differences between any

two rankings. The ranks are based on subjective criteria. Therefore, limited arith-

metic can be performed on ordinal variables, and mean and standard deviation of

the distribution of ordinal data is not deﬁned. Median and mode are relevant

descriptive statistics for this variable type.

(3) Nominal or categorical variables These variables are not numbers that can be

manipulated or ranked in any way but are observations according to which individ-

uals or objects in a sample can be classiﬁed. The non-numeric values that categorical

variables take on are mutually exclusive traits, attributes, classes, or categories that

all together are exhaustive. Examples of categorical variables include gender: male

or female, bacteria type: gram positive or gram negative, smoking status: smoker or

non-smoker, natural hair color: black, brown, red or blonde, and marital status:

single, married, divorced, or widowed. Based on the distribution of a categorical

variable within a sample, numbers can be assigned to each value of the categorical

variable, indicating the proportion of that category or trait within the sample.

In any experiment, measurements are made on people, animals, and objects such

as machines, solutions contained in beakers, or ﬂowing particles. Every individual or

229

4.3 Testing a hypothesis

experimental run that provides one measurement for a particular out come variable

is called an experimental unit. If only a single variable is measured per experimental

unit, then the data set is said to be univariate. Bivariate data result from measuring

two variables per experimental unit. When three or more variables are measured on

each experimental unit, the data are multivariate.

4.3.4 Choosing a hypothesis test

A number of factors must be considered when choosing a hypothesis test such as

(i) measurement scale of the random variable and (ii) characteristics of the popula-

tion distribution of the variable. Based on these two criteria alone, hypothesis tests

are broadly classiﬁed into three types.

(1) Parametric tests: These tests assum e that the measured variable exhibits a known

form (or shape) of distribution within the population. Parametric tests are geared

towards testing a hypothesis made about a population parameter such as mean or

variance of the population dist ribution. To make a statistical inference regarding the

value of a population parameter (e.g. mean), we must use the sampling distribution

of the corresponding sample-derived statistic under H

. The sampling distribution

of, say, the sample mean can only be determined if the probability distribution of

the random variable is well-deﬁned. (The central-limit theorem relaxes this con-

straint in many instances.) For example, the probability (sampling) distribution of

the mean of a sample (size n) derived from a normal population is also normal. The

variance of a sample (size n ) drawn from a normal population follows the χ

distribution.

(2) Distribution-free tests These tests do not require knowledge of the nature of the

distribution of the measured variable within the population. Some distribution-free

methods, such as the sign test, are designed to test hypotheses on the population

median.

(3) Non-parametric tests Non-parametric methods, by deﬁnition, do not make any

inference concerning population parame ters such as means, medians, or variances.

Examples of non-parametric tests are the χ

goodness of ﬁt test and the χ

test

for independence. However, these tests are not necessarily distribution-free. The χ

tests assume that the sample sizes are large enough for the central-limit theorem to

apply.

Distribution-free tests and non-parametric tests are usually grouped under a

single heading – non-parametric statistics. Non-parametric statistical analysis is

performed on all data that cannot be subjected to parametric tests. When the form

of variable distribution within a population is known, parametric tests are much

superior to non-parametric tests for hypothesis testing. Parametric tests have the

advantage of giving the most “bang for the buck” since they utilize information

contained in the data to the maximum potential to generate statistical inferences

regarding the concerned populations. Parametric tests have more statistical power

(less risk of making a type II error) than non-parametric tests and should always be

preferred if the data qualify for parametric testing.

Samples of the same size, when randomly drawn from the same population, will yield somewhat

different values of the same descriptive statistic, e.g. mean, median, or variance. A sampling distribution

is the probability distribution of all possible values of that statistic when all possible samples of some

pre-speciﬁed size are drawn from the reference population.

230

Hypothesis testing

When can you use a parametric test?

If the probability distribution of the measured variable in the population can be

described by a known, well-deﬁned functional form, then the sampling distribution

of the relevant sample-derived statistic (e.g. the sample mean) can be calculated. It is

then appropriate to use a parametric test to answer questions regarding population

characteristics such as the mean and variance.

If the population variable is cardinal, i.e. follows a ratio scale or interval scale, then

estimation of population parameters, such as mean and variance, is useful.

When should you use a non-parametric test?

When the variable type is ordinal or nominal.

When the underlying distribution of the variable within the popul ation is not known

and the sample size is not large enough for the central-limit theorem to apply.

When gross inequality of sample variances exist which preclude use of a t test or

ANOVA.

When transformation of a highly non-normal population variable does not produce

normality, or transformation does not resolve heteroscedasticity (inequality of

variances) in multi-sample data.

To summarize, we list below some important factors that you should consider

when choosing a hypothesis test. Speciﬁcs on how to choose a method of testing will

become clear er as we discuss each test separately.

Factors that govern the choice of the hypothesis test

(1) The type of variable: cardinal, ordinal, or nominal.

(2) The shape of the distribution curve of the variable: normal or non-normal.

(3) Equality or inequality of population variances when comparing two or more

samples.

(4) Sample size, for applicability of the central-limit theorem.

(5) Information that we seek from a test.

4.4 Parametric tests and assessing normality

Parametric tests are powerful because they allow you to deﬁne conﬁdence intervals for

population parameters and test hypotheses with greater precision. Many parametric

procedures require that the underlying distribution of the variables be normal,

e.g.

the z test, t test, and ANOVA (ANalysis Of VAriance). Use of the ANOVA method

hinges on a normal distribution of the population variable. For the z test and t test, the

normality requirement is not as strict when working with large samples. Fortunately,

the central-limit theorem relaxes the normality condition for large samples that have a

non-normally distributed variable. The mean of a large sample taken from a non-

normal population will have an approximately normal sampling distribution that

follows N μ; σ=

ﬃﬃﬃ

ðÞ,whereμ is the population mean, σ is the population standard

deviation, and n is the sample size. In this chapter, we only consider parametric tests

that are designed to analyze normal population distributions.

Other forms of continuous probability distributions include the uniform, exponential, lognormal, and

Weibull distributions.

231

4.4 Parametric tests and assessing normality

Before you can use a parametric test, you should ensure that your data meet the

normality criteria. The data do not need to be perfectly normal. Parametric tests

such as the z test, t test, and ANOVA are sufﬁciently robust that modest deviations

of the data from normality do not adversely affect the reliability of the test result.

Many distributions found in nature are close to normal wi th some modiﬁcations.

Some distributions are symmetric, but in some cases may have a narrower central

region and longer tails than the normal distribution, or alternatively a bulky central

region and shorter tails. Many times distributions are found to be approximately

normal but with asymmetric tails. Such distributions that have one tail longer

than the other are called skewed distributions. To assess whether the distribution is

acceptably normal, you need to test your data using one or more of several techni-

ques that check for normality.

A simple method to check for normality of data is to plot a histogram of the data.

You can visually inspect the histogram for symmetry and unimodal distribution. It is

often difﬁcult to tell if the distribution conform s to a normal shape, especially if

the number of data points is small. To check if the histogram shape is Gaussian,

you should calculate the mean μ and variance σ

of the data and superimpose the

normal curve N(μ, σ) on the histogram, after rescaling the area of the histogram to 1.

An overlay of both plots may yield more clues regarding the normality of the data.

However, when data points are few, the shape of the histogram is not obvious and

it may not be practical to use this method. Moreover, concluding whether a plot is

bell-shaped can be a subjective exercise.

Another method to check for normality is to generate a normal probability plot.A

probability plot graphs the data points arranged in ascending order against the

corresponding z (standard normal variable) values expected if the data were per-

fectly normal. If the data follow a normal distribution, then the plot will yield an

approximately straight line. Before we proceed with the description of this method,

we must introduce the concept of a quantile.

The cumulative distribution function Φ yðÞ¼

∞

fxðÞdx of a random variable y,

which was deﬁned in Chapter 3, calculates the cumulative probability of Pðx  yÞ

(f is the probability density function).

If n values of y, where y is defined by the cumulative distribution function Φ y

ðÞ

∞

ðÞ

dx;

y 2∞; ∞ðÞ; Φ 2 0 ; 1½, are chosen such they mark out (n + 1) equally spaced intervals on the Φ

scale within the entire interval of [0, 1], then each y point is called a quantile. Quantiles corresponding

to Φ yðÞ¼0orΦ yðÞ¼1 are not defined. If n = 3, each quantile is called quartile (4-quantile) since

the cumulative distribution has been divided into four equally sized intervals, and if n = 99 each

quantile is called a percentile (100-quantile).

For instance, if the cumulative distribution of a continuous random variable x is

divided into ten equally spaced intervals by nine 10-quantiles and the ﬁfth 10-

quantile is m, then Φ mðÞ¼Px mðÞ¼5=10 ¼ 0:5, which is the median of the

distribution. For the kth (n + 1)-quantile y, Φ yðÞ¼Px yðÞ¼k=ðn þ 1Þ. So far

in this discussion we have assumed that the probability density function used to

calculate the cumulative distribution is a continuous and well-deﬁned mathematical

function. If the data set is ﬁnite and the underlying probability distribution is

unknown, the quantiles must be calculated from the data points. For example, a

data set given below has ten values arranged in ascending order:

1:0; 1: 4 ; 1:8; 2:0; 2:1; 2:15; 2:2; 2:3; 2:5; 3:0:

232

Hypothesis testing

Each data point x

is randomly drawn and independent from each other, and

contributes equally to the cumulative probability. The median of this data set,

which is 2.125, divides the data into two subsets of equal intervals on the cumulative

probability scale, i.e. Px 2:125ðÞ¼1=2¼0:5; 50% of the data lie below the

median. The median of the ﬁrst subset is 1.8 and the median of the second subset

is 2.3. If the data are divided into quartiles, then 25% of the data are less than the ﬁrst

quartile, 50% of the data lie below the second quartile, and 75% of the data fall

below the third quartile. The ﬁrst, seco nd, and third quartiles are 1.8, 2.215, and 2.3,

respectively. Thus, the kth (n + 1)-quantile is the point below which k=ðn þ 1Þ

100% of the data lie.

Now let’s create a normal probability p lot to see if the data set given a bove is

normal. The data are already arranged in ascending order. We already have ten

quantiles but we need to calculate which kth quantile each data point represents.

There is no one method universally employed to calculate the value of a quantile,

and several methods are in use. For a data set containing n data points, the ith

data point is associated with the i  0:5ðÞ=nth quantile, i.e. the data points in

ascending order are the 0:5=nðÞth; 1:5=nðÞth; 2:5= nðÞth; ...; n  0:5ðÞ=nðÞth quan-

tiles. The data points along with the kth quantiles that they represent are listed in

Table 4.3.

The z values that correspond to the ð i 

0:5ðÞ=nÞth quantiles of the standard

normal

distribution are determined using the norminv function provided by

Statistics Toolbox . In other words, for each value of Φ zðÞwe want to determine z .

The corresponding z values are listed in Table 4.3.

Now, if the data points are truly normal, then the relationship between x and z is

given by x ¼ σz þ μ. If an approximately straight line results, we may conclude that

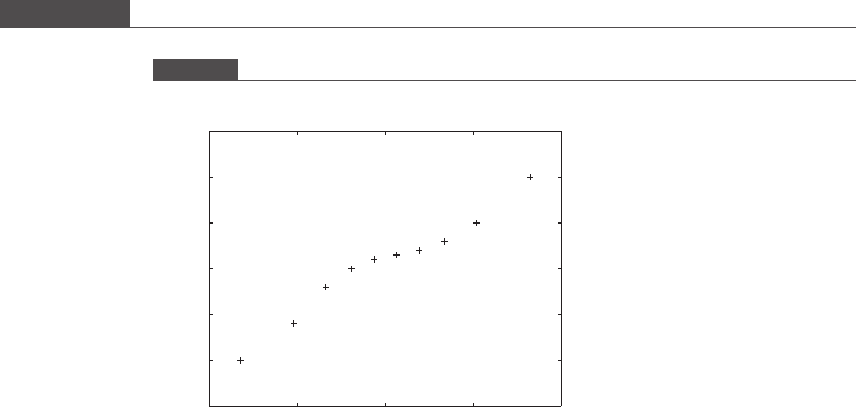
the data points follow a normal distribution. In Figure 4.4 x is plotted against z.

Keep in mind that even a set of perfectly normal data points will not produce a

straight line because of inherent sampling variability. If the probability plot takes on

a distinctly curved shape, such as a “C” or an “S” shape, then the distribution of the

data is non-normal. In Figure 4.4, the plot has several bends and kinks, indicating

that the distribution of the data is probably non- normal.

Table 4.3 Data points and their corresponding z quantiles

Serial number, i Data points, x

kth quantile,

Φ zðÞ¼

i0:5ðÞ

Standard normal

quantile, z

1 1.0 0.05 −1.6449

2 1.4 0.15 −1.0364

3 1.8 0.25 −0.6745

4 2.0 0.35 −0.3853

5 2.1 0.45 −0.1257

6 2.15 0.55 0.1257

7 2.2 0.65 0.3853

8 2.3 0.75 0.6745

9 2.5 0.85 1.0364

10 3.0 0.95 1.6449

233

4.4 Parametric tests and assessing normality

Using MATLAB

The function normplot offered by Statistics Toolbox creates a normal probability

plot. The syntax for this function is

normplot(x)

where x is the data set to be assessed for normality. The function normplot plots

the data points along the x-axis and the cumulative probability (in place of the z

quantiles) along the y-axis. On this plot, the 25th and 75th percent iles are joined by a

solid red line. This line extends in either direction as a dashed line. Try using the

normplot function to obtain a probability plot for the data set above.

Statistical tests that quantitatively measure the ﬁt of the observed sample distribu-

tion to the expected normal distribution are called goodness-of-ﬁt tests. These tests

are more sophisticated and also more conclusive than using normal probability

plots. The χ

goodness-of-ﬁt test is one example of a goodness-of-ﬁt test that can

be used to calculate the deviations of data from normality. This test is discussed

in Section 4.9.1. Other popular statistical tests for assessing normality include the

Kolmogorov–Smirnov one-sample test and the Shapiro–Wilks test. The latter

method uses a normal probability plot for calculating the Shapiro–Wilk statistic.

These methods are not discussed here. Statistics Toolbox supplies functions that

perform the χ

goodness-of-ﬁt test and the Kolmogorov–Smirnov one-sample test.

If the data are found to be non-normal, you can either choose to evaluate the data

using a non-parametric test or use a transformation to convert the data to a normal

distribution. Not all data can be transformed to a bell-shaped distribution. Another

option is to use a parametric test based on another probability distribut ion. You will

need to refer to advanced statistical texts for these statistical methods. Finally, you

can proceed with a parametric test anyway, despite the non-normality of the data.

The test may produce inaccurate results and you should be cautious of how you

interpret the p value. You may want to use a more conservative signiﬁcance level,

such as α = 0.01, to improve the reliability of your conclusion.

Figure 4.4

Normal probability plot.

−2 −1 0 1 2

0.5

1.5

2.5

3.5

z quantiles

Data points x

234

Hypothesis testing

4.5 The z test

You are already famili ar with several aspects of the z test from the discussion on

hypothesis testing in Section 4.3. The z test is a parametric test used to compare the

means of two samples or compare a sample mean to an expected value. In order to

apply the z test, the variance of the populations from which the samples are drawn

must be known. The z test is used in the following two ways.

(A) The one-sample z test is used to compare a sample mean with a population mean.

Here, you want to determ ine if the sample was obtained from a certain population

with already established parameters, i.e. the mean and variance of the population is

known. This scenario was discussed in Section 4.3.

(B) The two-sample z test is used to compare the means of two random independent

samples such as a control sample and a treated sample. Here you are trying to

determine whether there is any effect of the treatment, for instance.

The conditions for using the z test are as follows.

(1) The population must be normal if the sample size is small. This ensures that the

sampling distribution of the sample mean is also normally distributed. However, if

the sample is large enough so that the central-limit theorem applies, then the

sampling distribution of the mean will be normal regardless of the population

distribution of the random variable.

(2) The variance of the populations being compared must be known. This may appear to

be a serious limitation, since, most often, the purpose of the experiment is to estimate

unknown population parameters and therefore we do not know the population

variance beforehand. However, if the sample size is large (usually n > 30) the sample

variance often reliably estimates the population variance.

Note the dual advantage of a large sample size – the central-limit theorem ensures

approximate normality of the sampling distribution of the mean and we obtain an

accurate estimate of the population variance. A large sample drawn from a non-

normal population whose variance is unknown will still satisfy both requirements of

the z test. A large sample size has several additional advantages, such as greater

precision of an interval estimate of the population mean and improved power of a test.

If the sample size is small, the sample variance will not be an accurate estimate of

the population variance. In this case, you can use the t test provided that the variable

is normally dist ributed within the reference population. The t test is discussed in

Section 4.6. For small samples drawn from non-normal populations, you can choose

to either transform the data to normalize the distribution or use a non-parametric

test (see Section 4.10).

With this knowledge in hand, we redeﬁne situations for which the z test can be used.

(A) To determine if a sample is drawn from a populati on with known parameters. The

population must be normal if the sample size is small. The normality requirement is

relaxed if the sample size is large.

(B) To compare the means of two independent large random samples.

4.5.1 One-sample z test

A one-sam ple z test is used to determine if a sample belongs to a population whose

statistics – namely mean and variance – are established. The method of using this test

235

4.5 The z test

was illustrated in detail in Section 4.3. A one-sample z test can also be carried out in

MATLAB.

Using MATLAB

Statistics Toolbox contains the function ztest, which performs a one-sample z test.

The syntax for ztest is

[h, p] = ztest(x, mu, sigma, alpha, tail)

ztest has a variety of syntax options of which only one is listed above. The function

arguments are

x: the vector of sample values,

mu: mean of the population from which the sample is derived under the null

hypothesis,

sigma: standard deviation of the population from which the sample has come

from under the null hypothesis,

alpha: the signiﬁcance level, and

tail: speciﬁes the directionality of the hypothesis and takes on the values

‘both’, ‘right’, or ‘left’.

The ztest function outputs the following:

h: the hypothesis test result – 1 if null hypothesis is rejected at the alpha

signiﬁcance level and 0 if null hypothesis is not rejected at the alpha

signiﬁcance level.

p: p value.

Type help ztest for additional features of this function.

In this section we explore how to determine the power of a one-sample z test. The

power of a test (1 – β) is its ability to recognize a true difference between the

populations under study. Let’s set up a non-directional hypothesis:

: μ ¼ μ

; H

: μ 6¼ μ

;

where μ is the mean of the population from which our sample has been taken and μ

is the expected value under the null hypothesis. We want to know if the population

that our sample represents has the same mean as that of a certain population

characterized by the statistics μ

; σ



. The sample mean is calculated to be



x from

n individual units. The z test requires that either n is large or that the population

variable x is distributed normally. The variance σ

is known and assumed to be the

same for either population.

If the null hypothesis is true, then the sample mean



x follows the normal distri-

bution N μ

; σ=

ﬃﬃﬃ

ðÞ.

If the alternate hypothesi s is true, then μ ¼ μ

, where μ

6¼ μ

. In that case,



follows the normal distribution N μ

; σ=

ﬃﬃﬃ

ðÞ. The mean or midpoint of the distribu-

tion of sample means under the null hypothesis and under the alternate hypothesis

will be separated by a distance equal to μ

 μ

(see Figure 4.5). The two distributions

predicted by the two complementary hypotheses may overlap each other. The extent

of overlap of the two distributions depends on the width of each distribution, which

236

Hypothesis testing