King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

is determined by σ=

ﬃﬃﬃ

and on the difference between the population means, μ

 μ

The area under the curves that are free from overlap determines the ability to discern

or “resolve” a difference between the two population means. If a large amount of

area under the N μ

; σ=

ﬃﬃﬃ

ðÞdistribution curve lies within the N μ

; σ=

ﬃﬃﬃ

ðÞdistribu-

tion curve, the calculated z statistic will most likely yield a non-signiﬁcant result,

even if H

is true. Under these circumstances, the power of the test is low and the risk

of making a type II error is high. On the other hand, minimal overlap of the null

distribution with the distribution corresponding to the alternate hypothesis affords

large power to the z test.

We want to have as large a power a s economically feasible so that if H

is true, we

will have maximized our chan ces to obtain a signiﬁcant difference. Let’s assume that

the alternate hypothesis is true, and additionall y that μ

.InFigure 4.5, both

distributions representative of the null and the alternate hypotheses are shown. The

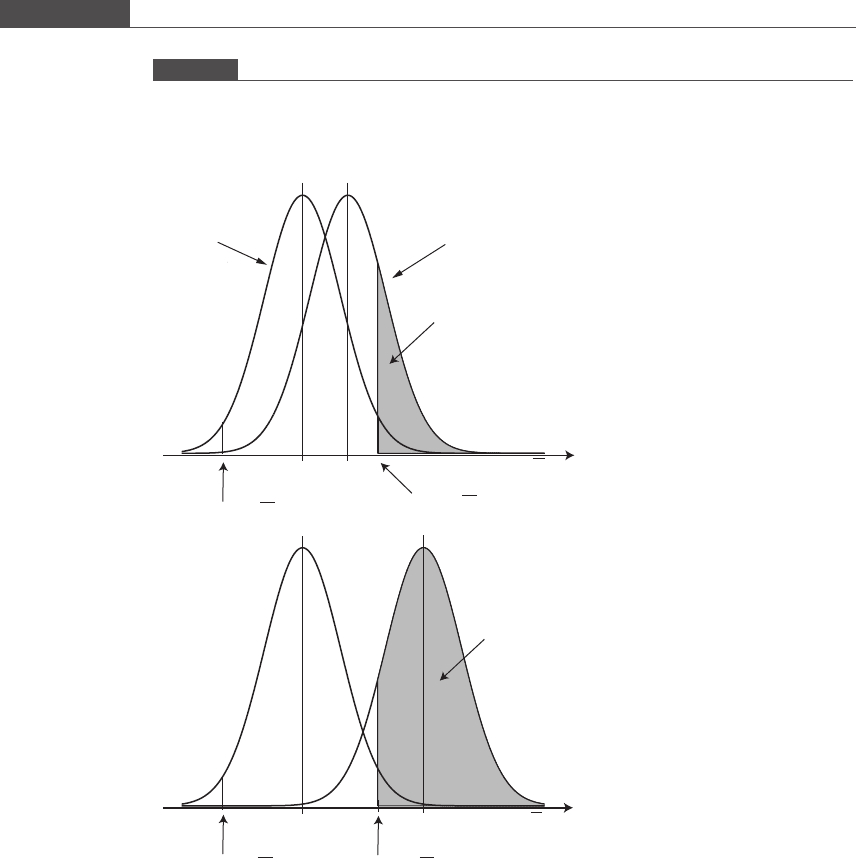
Figure 4.5

The power of a non-directional one-sample z test. The shaded region is the area under the H

distribution that

contributes to the power of the z test. We have σ = 4 and α/2 = 0.025. (a) μ

 μ

¼ 1:5; (b) μ

 μ

¼ 4:0. The power

increases as μ

moves further away from μ

1–β

+ z

α/2

σ/√n

(a)

(b)

curve

+ z

1–α/2

σ/√n

1–

+ z

α/2

σ/√n μ

+ z

1–α/2

σ/√n

237

4.5 The z test

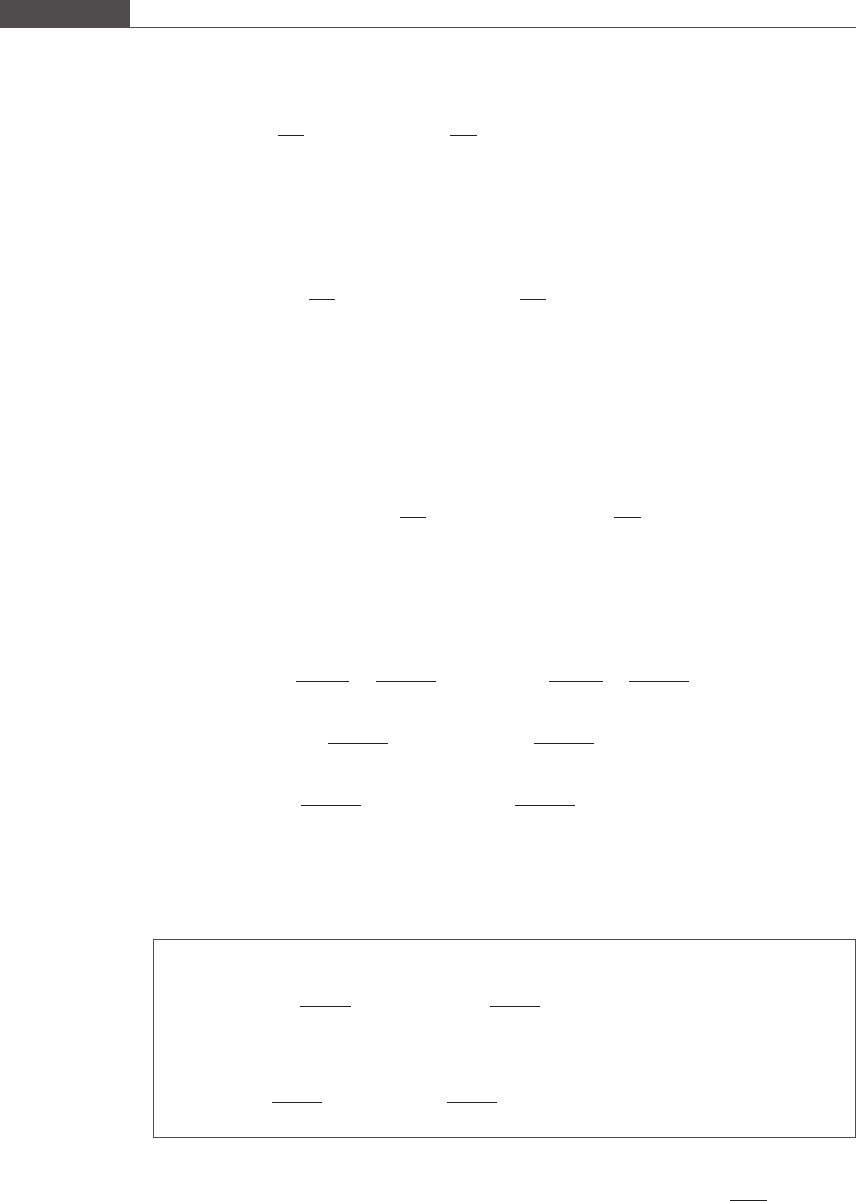
signiﬁcance level that deﬁnes the null hypothesis rejection criteria is ﬁxed at α. If the

sample mean



x lies in the interval

þ z

α=2

ﬃﬃﬃ



þ z

1α=2

ﬃﬃﬃ

;

then we retain the null hypothesis. This interval represents 100(1 – α) % of the area

under the null distribution that forms the non-rejection region for the z test. When

is true and the sample mean falls within this interval, a type II error (false

negative) results. On the other hand, if



þ z

α=2

ﬃﬃﬃ



þ z

1α=2

ﬃﬃﬃ

;

then



x lies in the rejection region (see Figure 4.1) and we reject H

. Since



x follows the

N μ

; σ=

ﬃﬃﬃ

ðÞdistribution, the area under this distribution that overlaps with the non-

rejection region of the null distribution deﬁnes the probability β that we will make a

type II error. Accordingly, the area under the alternate distribution of sample means

that does not overla p with the non-rejection region of the null distribution deﬁnes

the power (1 – β)ofthez test (see Figure 4.5). The power is calculated as follows:

1 β ¼ P



þ z

α=2

ﬃﬃﬃ



þ P



þ z

1α=2

ﬃﬃﬃ



The probability is calculated using the cumulative distribution function of the

standard normal distribution. We convert the



x scale shown in Figure 4.5 to the z

scale. The power is calculated as follows:

1 β ¼ P



x  μ

σ=

ﬃﬃﬃ

 μ

σ=

ﬃﬃﬃ

þ z

α=2



þ P



x  μ

σ=

ﬃﬃﬃ

 μ

σ=

ﬃﬃﬃ

þ z

1α=2



¼ Pz

 μ

σ=

ﬃﬃﬃ

þ z

α=2



þ Pz

 μ

σ=

ﬃﬃﬃ

þ z

1α=2



¼ Φ

 μ

σ=

ﬃﬃﬃ

þ z

α=2



þ 1 Φ

 μ

σ=

ﬃﬃﬃ

þ z

1α=2



Although we have developed the above expression for the power of a non-

directional one-sample z test assuming that μ

, this expression also applies for

the case where μ

. You should verify this for yourself.

The power of a non-directional one-sample z test is given by

1 β ¼ Φ

 μ

σ=

ﬃﬃﬃ

þ z

α=2



þ 1 Φ

 μ

σ=

ﬃﬃﬃ

þ z

1α=2



: (4:4)

When H

is true, the probability of making a type II error is

β ¼ Φ

 μ

σ=

ﬃﬃﬃ

þ z

1α=2



 Φ

 μ

σ=

ﬃﬃﬃ

þ z

α=2



: (4:5)

Just by looking at Figures 4.5(a) and (b), we can conclude that the area under the

curve to the left of the ﬁrst critical value z

α=2

, which is equal to Φ

μ

σ=

ﬃﬃ

þ z

α=2



,is

negligible compared to the area under the H

curve to the right of the second critical

238

Hypothesis testing

value z

1α=2

. The power of a non-directional one-sample z test when μ

approximately

1 β  1 Φ

 μ

σ=

ﬃﬃﬃ

þ z

1α=2



What if the hypothesis is one-sided? Let’s revise the alternate hypothesis to

: μ

. For this one-sided test, the rejection region is conﬁned to the right tail

of the null distribution.

The power of the directional one-sample z test for H

: μ

is calculated as

1 β ¼ 1 Φ

 μ

σ=

ﬃﬃﬃ

þ z

1α



: (4:6)

Similarly, the power of the directional one-sample z test for H

: μ

is calculated as

1 β ¼ Φ

 μ

σ=

ﬃﬃﬃ

þ z



: (4:7)

The derivation of Equations (4.6) and (4.7) is left to the reader.

To estimate the power of a test using Equations (4.4),(4.6), and (4.7), you will need

to assume a value for μ

. An estimate of the population variance is also required.

A pilot experimental run can be performed to obtain preliminary data for this purpose.

Frequently, these formulas are used to calculate the sample size n in order to attain the

desired power 1 – β. Calculating sample size is an important part of designing experi-

ments; however, a detailed discussion of this topic is beyond the scope of this book.

Based on the equations developed in this secti on for calculating the power of a

one-sample z test, we can list the factors that inﬂuence statistical power.

(1) μ

 μ

The difference between the true mean and the expected value under the

null hypothesis determines the separation distance between the two distributions.

Figure 4.5(a) demonstrates the low power that results when μ

 μ

is small, and

Figure 4.5(b) shows the increase in power associated with a greater μ

 μ

differ-

ence. This factor cannot be controlled; it is what we are trying to determine.

(2) σ The variance determines the spread of each distribution and therefore affects the

degree of overlap. This factor is a property of the system and cannot be controlled.

(3) n The sample size affects the spread of the sampling distribution and is the most

important variable that can be increased to improve power. Figure 4.6 illustrates the

effect of n on power.

Figure 4.6

The power of the one-sample z test improves as sample size n is increased. The shaded area under the H

distribution is

equal to the power of the z test. We have σ =4,α/2 = 0.025, and μ

 μ

¼ 2:0.

n = 10

= 20 n = 30

239

4.5 The z test

(4) z

Critical values of z that specify the null hypothesis rejec tion criteria reduce

power when α is made very small. Suitable values of z

are chosen in order to balance

the risks of type I and type II errors.

Example 4.2

A vaccine is produced with a mean viral concentration of 6000 plaque-forming units (PFU) per dose and a

standard deviation of 2000 PFU per dose. A new batch of vaccine has a mean viral concentration of 4500

PFU per dose based on a sample size of 15. The efficacy of a vaccine decreases with a decrease in viral

count. Is the mean viral concentration of the new batch of vaccines significantly different from the desired

amount? In order to determine this we perform a one-sample z test.

We state our hypotheses as follows:

: “The new batch of vaccines has a mean viral concentration equal to the specified value, μ ¼ μ

.”

: “The new batch of vaccines has a mean viral concentration different from the specified value,

μ 6¼ μ

.”

Our sample mean is



x ¼ 4500. The mean of the population from which the sample is taken under the

null hypothesis is μ

= 6000. The standard deviation of the population is σ = 2000.

The z statistic is calculated as

z ¼

4500  6000

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2000

=15

¼2:905:

The p value associated with this test statistic value is calculated using Equation (4.2) for a two-sided

hypothesis. Statistics Toolbox’s normcdf function can be used to obtain the p value. Typing the following

statement in MATLAB

p = 2*(1-normcdf(2.905, 0, 1))

MATLAB outputs

0.0037

Thus, the probability of obtaining a value of the test statistic as far removed or further from zero as 2.905

is 0.0037. Since 0.0037 < 0.05 (by an order of magnitude), this result is highly significant and we

conclude that there is sufficient evidence to reject the null hypothesis. The new batch of vaccines has a

mean viral concentration that is different (less) than the desired concentration.

Alternatively, we can perform the one-sample z test using the MATLAB hypothesis testing function

ztest. The significance level is set at α = 0.05.

In the Command Window, we type

[h, p] = ztest(4500, 6000, sqrt(2000^2/15), 0.05, ‘both’)

Note that because we do not have a vector of values, but instead are providing the sample mean,

MATLAB does not have an estimate of the sample size. Therefore, we supply in place of the standard

deviation of the population, the SEM. MATLAB outputs

0.0037

Next, we calculate the power of the one-sample z test to resolve a population mean viral concen-

tration of μ = 4500 PFU per dose from the population specified by quality control. The power (1 – β)is

the probability that we will obtain a z statistic that will lead us to reject the null hypothesis when the

sample has been drawn from a population with mean viral concentration 4500 PFU per dose and the

240

Hypothesis testing

hypothesized mean under H

is 6000 PFU per dose. Using Equation (4.4), we estimate the power of the

test. Since μ

1 β  Φ

 μ

σ=

ﬃﬃﬃ

þ z

α=2



Typing the following statement

power = normcdf((6000–4500)/(2000/sqrt(15)) — 1.96)

we obtain

power =

0.8276

The probability that we will correctly reject the null hypothesis is 0.8276. In other words, if this

experiment is repeated indefinitely (many, many independent random samples of size n = 15 are drawn

from a population described by N(4500, 2000)), then 82.8% of all experiments will yield a p value ≤ 0.05.

Thus, there is a 17.24% chance of making a type II error.

4.5.2 Two-sample z test

There are many situations that require us to compare two populations for anticipated

differences. We may want to compare the product yield of two distinct processes, the

lifetime of material goods supplied by two different vendors, the concentration of drug

in a solution produced by two different batches, or the effect of temperature or

humidity on cellular processes. The two-sample z test, which is used to determine if

a statistical difference exists between the populations, assumes that the random

samples derived from their respective populations are independent. For example, if

two measurements are derived from every individual participating in the study, and

the ﬁrst measurement is allotted to sample 1 while the second measurement is allotted

to sample 2, then the samples are related or dependent. In other words, the data in

sample 1 inﬂuence the data in sample 2 and they will be correlated. The two-sample z

test is inappropriate for dependent samples. Another method called the paired t test

should be used to test hypotheses when the experiment produces dependent samples.

Assume that two random independent samples are drawn from two normal

populations or two large samples are drawn from populations that are not necessa-

rily normal. The two complementary non-directional hypotheses concerning these

two populations are:

: “The population means are equal, μ

¼ μ

.”

: “The population means are unequal, μ

6¼ μ

.”

If the null hypothesis of no difference is true, then both populations will have the

same mean. We expect the respective sample means



and



to be equal or similar

in value. If we subtract one sample mean from the other,







, then the difference

of the means will usually be close to zero. Since the sampling distribution of each

sample mean is normal, the distribution of the difference between two sample means

is also normal. The mean of the sampling distribution of the difference between the

two sample means,







, when H

is true, is







ðÞ¼E



ðÞE



ðÞ¼μ

 μ

¼ 0:

What is the variance of the sampling distribution of the difference of two sample

means? In Chapter 3, you learne d that when we combine two random variables

241

4.5 The z test

arithmetically, the variance of the result is calculated based on certain prescribed

rules. When one random variable is subtracted from the other,

z ¼ x  y;

the variance of the result is

¼ σ

þ σ

 2σ

: (3:40)

When the random variable measurements are independent of each other, the cova-

riance σ

¼ 0.

Let z ¼







. Suppose σ

and n

are the variance and size of sample 1, and σ

and n

are the variance and size of sample 2, respectively. The standard deviation of

the sampling distribution of the difference of two sample means is called the standard

error and is given by

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

When the null hypothesis (H

: μ

¼ μ

) is true, then the statistic calculated below

follows the standard normal distribution:

z ¼







ðÞμ

 μ

ðÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

: (4:8)

Equation (4.8) is the z statistic used to test for equality of two population means.

Since μ

 μ

¼ 0, we simplify Equation (4.8) to

z ¼







ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

: (4:9)

Example 4.3 Properties of biodegradable and metallic stents

Stents are used to prop open the interior of lumenal structures, such as arteries, gastrointestinal tracts,

such as the esophagus, duodenum, and colon, and the urinary tract. Such interventions are required when

diseased conditions such as atherosclerosis, advanced-stage tumors, or kidney stones restrict the flow of

fluid or interfere with the passage of material through the conduit. Because of the wide range of

applications that stents serve, these prosthetic devices have a multitude of design options, such as size,

material, mechanical properties, and structure. Metallic stents were developed initially, but certain draw-

backs with using permanent metallic stents have spurred the increased interest in designing biodegradable

polymeric stents. A major challenge associated with polymer stents lies in overcoming difficulties

associated with deployment to the intended site. Specifically, the goal is to design polymeric stents with

suitable mechanical/structural properties that enable quick and safe deliver y to the application site, rapid

expansion, and minimal recoil.

A new biodegradable polymeric stent has been designed with a mean elastic recoil of 4.0 ± 2.5%. The

recoil is measured after expansion of the stent by a balloon catheter and subsequent deflation of the

balloon. The sample size used to estimate recoil characteristics is 37. Metallic stents (n = 42) with

comparable expansion properties have a mean recoil value of 2.7 ± 1.6%. We want to know if the recoil

property is different for these two populations of stents.

The complementary hypotheses are:

: “The recoil is the same for both metallic stents and polymeric stents considered in the study,

¼ μ

.”

242

Hypothesis testing

: “The recoil is different for the two types of stents, μ

6¼ μ

.”

We set the significance level α = 0.05. Since n

and n

> 30, we can justify the use of the two-sample z

test. The critical values of z for the two-sided test are −1.96 and 1.96.

The test statistic is calculated as

z ¼

4:0  2:7

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2:5

1:6

¼ 2:708:

The p value corresponding to this test statistic is 21Φ zðÞðÞ.

At the MATLAB command prompt, we type

z=2.708;

p = 2*(1-normcdf(z,0,1))

MATLAB outputs

0.0068

Since p < 0.05, we reject H

. We conclude that the mean recoil properties of the two types of stents are

not equal. We can also use the MATLAB function ztest to perform the hypothesis test. Since







¼ 1:3 and the standard error

SE ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

¼ 0:48;

[h, p] = ztest(1.3, 0, 0.48, 0.05, ‘both’)

0.0068

The power of a two-sample z test is calcul ated in a similar fashion as demonstrated

for a one-sample z test. For a one-sample z test, we wish to maximize power by

increasing the resolvability between the sampling dist ribution of the sample mean

under the null hypothesis and that under the alternate hypothesis. In a two-sample z

test, we calculate the degree of non-overlap between the sampling distributions of the

difference between the two sample means under the null hypothesis and the alternate

hypothesis. We assume a priori that the true difference between the two population

means under H

: μ

6¼ μ

is some speciﬁc value μ

 μ

¼ Δμ 6¼ 0, and then proceed

to calculate the power of the test for resolving this difference.

The power of a non-directional two-sample z test, where z is calculated using Equation (4.9),is

1 β ¼ Φ

Δμ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ z

α=2

þ 1 Φ

Δμ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

þ z

1α=2

; (4:10)

where Δμ is the assumed difference between the two population means under H

Using the method illustrated in Secti on 4.5.1, you may derive Equation (4.10)

on your own.

243

4.5 The z test

4.6 The t test

As discussed in Section 4.5, use of the z test is limited since the variance of the

population distribution is usually unknown and the sample sizes are often small. For

normal population(s), when the only available estimate for the population varia nce

is the sample variance, the relevant statistic for constructing conﬁdence intervals and

performing hypothesis tests is the t statistic given by Equation (3.35),

t ¼



x  μ

ﬃﬃﬃ

: (3:35)

The Student’s t distribution, which was discussed in Chapter 3, is the sampling

distribution of the t statistic and is a function of the degrees of freedom f available

for calculating the sample standard deviation s . In this section, we discuss how the t

statistic can be used to test hypotheses pertaining to the population mean. The

method of conducting a t test is very similar to the use of the z tests discussed in

Section 4.5. The p value that corresponds to the calculated value of the test statistic t

depends on whether the formulated hypothesis is directional.

For a two-sided t test, p is calculated as

p ¼ 21 Φ

tjjðÞðÞ; (4:11)

whereas for a one-sided t test

p ¼ 1 Φ

ðÞðÞ; (4:12)

where Φ

is the cumulative distribution function for the Student’s t distribution and f is the degrees of

freedom associated with t.

4.6.1 One-sample and paired sample t tests

The one-sample t test is used when you wish to test if the mean



x of a single sample is

equal to some expected value μ

and the sample standard deviation is your only

estimate of the population standard deviation. The variable of interest must be

normally distributed in the population from whi ch the sample is taken. The t test

is found to be accurate for even moderate departures of the population from

normality. Therefore, the t test is suitable for use even if the population distribution

is slightly non-normal. As with the z test, the sample must be random and the sample

units must be independent of each other to ensure a meaningful t test result.

Using MATLAB

Statistics Toolbox contains the function ttest, which perfor ms a one-sample t test.

The syntax for ttest is

[h, p] = ttest(x, mu, alpha, tail)

This is one of many syntax options available. The function parameters are:

x: the vector of sample values,

mu: mean of the population from which the sample is derived under the null

hypothesis,

244

Hypothesis testing

alpha: the signiﬁcance level, and

tail: speciﬁes the directional ity of the hypothesis and takes on values:

‘both’, ‘right’,or‘left’.

MATLAB computes the sample standard deviation, sampl e size, and the degrees

of freedom from the data values stored in x.

The ttest function outputs the following:

h: the hypothesis test result: 1 if null hypothesis is rejected at the alpha signiﬁcance

level and 0 if null hypothesis is not rejected at the alpha signiﬁcance level,

p: p value.

Type help ttest for viewing additional features of this function.

The metho d of conducting a one-sample t test is illustrated in Example 4.4.

Example 4.4

The concentration of a hemoglobin solution is measured using a visible light monochromatic spectro-

photometer. The mean absorbance of green light of a random sample consisting of ten batches of

hemoglobin solutions is 0.7 and the standard deviation is 0.146. The individual absorbance values are

0.71, 0.53, 0.63, 0.79, 0.75, 0.65, 0.74, 0.93, 0.83, and 0.43. The absorbance values of the hemoglobin

solutions are approximately normally distributed. We want to determine if the mean absorbance of the

hemoglobin solutions is 0.85.

The null hypothesis is

: μ ¼ 0:85:

The alternate hypothesis is

: μ 6¼ 0:85:

Calculating the t statistic, we obtain

t ¼

0:7  0:85

0:146=

ﬃﬃﬃﬃﬃ

¼3:249:

The degrees of freedom associated with t is f = n – 1=9.

The p value associated with tf¼ 9ðÞ¼3:249 is calculated using the tcdf function in MATLAB:

p = 2*(1-tcdf (3.249,9))

0.0100

Since p < 0.05, we reject H

The test procedure above can be performed using the MATLAB ttest function. We store the ten

absorbance values in a vector x:

x = [0.71, 0.53, 0.63, 0.79, 0.75, 0.65, 0.74, 0.93, 0.83, 0.43];

[h, p] = ttest(x, 0.85, 0.05, ‘both’)

0.0096

245

4.6 The t test

Alternatively, we can test the null hypothesis by constructing a confidence interval for the sample mean

(see Section 3.5.5 for a discussion on defining confidence intervals using the t statistic).

The 95% confidence interval for the mean population absorbance is given by

0:7  t

0:975;9

0:146

ﬃﬃﬃﬃﬃ

Using the MATLAB tinv function we get t

0:975;9

¼ 2:262.

The 95% confidence interval for the population mean absorbance is 0.596, 0.804. Since the interval

does not include 0.85, it is concluded that the hypothesized mean is significantly different from the

population mean from which the sample was drawn.

Note that the confidence interval gives us a quantitative measure of how far the hypothesized mean lies

from the confidence interval. The p value provides a probabilistic measure of observing such a difference, if

the null hypothesis is true.

Many experimental designs generate data in pairs. Paired data are produced when a

measurement is taken either from the same experimental unit twice or from a pair of

similar or identi cal units. For example, the effects of two competing drug candidates

or personal care products (e.g. lotions, sunscreens, acne creams, and pain relief

creams) can be compared by testing both products on the same individual and

monitoring various health indicators to measure the performance of each product.

If two drugs are being compared, then the experi mental design protocol usually

involves administering one drug for a certain period of time, followed by a wash-out

period to remove the remnant effects of the ﬁrst drug before the second drug is

introduced. Sometimes, the potency of a drug candidate may be contrasted with the

effect of a placebo using a paired experimental design. In this way, the individuals or

experimental units also serve as their own con trol. In cross-sectional observational

studies, repeated measurements on the same individual are not possible. Pairing in

such studies usually involves ﬁnding matched controls.

Paired designs have a unique advantage over using two independent samples to

test a hypothesis regarding a treatment effect. When two measurements x

and x

are

made on the same individual under two different conditions (e.g. administration of

two different medications that are meant to achieve the same purpose, measurement

of breathing rate at rest and during heavy exercise) or at two different times (i.e.

progress in wound healing under new or old treatment methods), one measurement

can be subtracted from the other to obtain a difference that measures the effect of the

treatment. Many extraneous factors that arise due to differences among individuals,

which can potentially confound the effect of a treatment on the measured variable,

are eliminated when the difference is taken. This is because, for each individual, the

same set of extraneous variations equally affects the two measurements x

and x

Ideally, the difference d ¼ x

 x

exclusively measur es the real effect of the treat-

ment on the individual. The observed variations in d from individual to individual

are due to biological (genetic and environmental) differences and various other

extraneous factors such as diet, age, and exercise habits.

Many extraneous factors that contribute to variations observed in the population

are uncontrollabl e and often unknown (e.g. genetic inﬂuences). When pairing data,

it is the contributions of these entrenched extraneous factors that cancel each other

and are thereby negated. Since each d value is a true measure of the treatment effect

and is minimally inﬂuenced by confounding factors, the paired design is more

efﬁcient and lends greater precision to the experimental result than the independent

246

Hypothesis testing