King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

hand, equations that exhibit stability (change in solution is on the same order of

magnitude as ﬂuctuations in the equation parameters) constitute a well-conditioned

problem. The conditioning of a system of equations depends on the determinant of

the coefﬁcient matrix.

(9) The condition number is a measure of the conditioning of a system of linear equations

and is deﬁned as cond AðÞ¼kAkkA

1

k, where A is the coefﬁcient matrix. Note that

cond(A) can take on values from one to inﬁnity. Low condition numbers close to one

indicate a well-conditioned coefﬁcient matrix. An ill-conditioned problem has a

large condition number.

Linear regression

(1) Experimental studies yield quantitative values that describe a relationship between

a dependent variable y and one or more independent variables x. It is useful to

obtain a mathematical model that relates the variables in the data set. The technique

of determining the model parameters that best describe the relationship between the

variables is called regression.

(2) The “best-ﬁt” curve obtained on regressing data to the model approximates the data

to within some degree but does not predict the original data points exactly. The

residual is deﬁned as the difference between the experimentally obtained value of y

and that predicted by the model. The residual (error) minimization criterion used to

obtain the “best-ﬁt” curve is called the objective function.

(3) In linear regres sion , the function al dependence of the dependent variable y on the

model parameters is strictly linear. Since the number of data points is greater than

the number of unknowns, the system of linear equations is overdetermined and an

exact solution does not exist.

(4) The linear least-squares criterion minimizes the sum of the squared residuals for an

overdetermined system. This criterion produces the normal equations A

Ac ¼ A

which on solving yields c, the vector containing the model parameters. Note that A is

the coefﬁcient matrix, and its size and structure depends on the model and the

number of data points in the data set.

(5) The coefﬁcient of determination, R

, measures the quality of the ﬁt between the model

and the data set; R

compares the sum of the squared residuals from the least-squares

ﬁt,

y 

yðÞ

, to the sum of the squared deviations,

y 



yðÞ

2.14 Problems

Solving systems of linear equations

2.1. Types of solutions for systems of linear equations.

(a) Each equation below represents a straight line. If two lines intersect at one point,

then the system of two lines is said to possess a “unique solution.” What type of

solution do the following systems of equations (lines) have? Determine by solving

the equations by hand. Also plot the equations (lines) using MATLAB (plot

function) to understand the physical signiﬁcance. In two-dimensional space, how

are lines oriented with respect to each other when no solution exists, i.e. the system

is inconsistent? What about when there exist inﬁnitely many solutions?

(i) 2x þ 3 y ¼ 3; x þ 2y ¼ 1;

(ii) x þ 2y ¼ 5; 3x þ 6y ¼ 15;

(iii) 2x þ 3y ¼ 5; 4x þ 6y ¼ 11.

127

2.14 Problems

(b) What value(s) sho uld p take for the system of the following two linear equations

to be consistent? (Hint: Determine the rank of the coefﬁcient matrix and the

augmented matrix. For what value of p is the rank of the augmented matrix

equal to that of the coefﬁcient matrix? You may ﬁnd it useful to use elementary

row transformations to simplify the augmented matrix.)

2x  3y ¼ 4;

4x  6y ¼ p:

What value(s) should p take for the system of two linear equations given below to be

inconsistent (no solution)? Does a unique solution exist for any value of p?Whyor

why not? Explain the situation graphically by choosing three different numbers for p.

2.2. Linear independence Show that the vectors

; v

2

are linearly independent. To do this, rewrite the vector equation

þ k

þþk

¼ 0

as Ak = 0, where A consists of v

, v

, and v

as column vectors and k is the

coefﬁcients vector, and solve for k.

2.3. Use of ﬁnite-precision in solving systems of equations You are given the following

system of equations:

5

þ 10

5

þ x

¼ 0:99998;

10

5

þ 10

5

 4x

¼ 6  10

5

;

þ x

þ 3x

¼ 1:

(a) Does this set of equations have a solution? (Hint: Check to see if rank(A) = rank

(aug A).)

(b) Solve the above system of equations by hand using four-digit arithmetic and

Gaussian elimination without pivoting. Substitute the solution back into the

equation. Does the solution satisfy the equations? Re-solve by including partial

pivoting. Are the solutions different?

exactly satisfy the equations?

(d) What is the condition number of this system? Change the right-hand side

constant of the ﬁrst equation, 0.9998, to 1. Do you get an exact solution

using only six-digit arithmetic? What is the relative change in solution com-

pared to the relative change made in the right-hand-side constant? Note the

importance of using greater precision in numerical computations. Often by

using greater precision, problems having large condition numbers can remain

tractable.

2.4. Pharmacokinetic modeling for “animal-on-a-chip” – 1 A material balance is

performed for naphthalene epoxide (NO) generation, consumption, and transport

in the μCCA device described in Figure 2.1; NO is an intermediate formed during the

metabolism of naphthalene.

Routes of generation of naphthalene epoxide:

(1) conversion of naphthalene into its epoxide.

128

Systems of linear equations

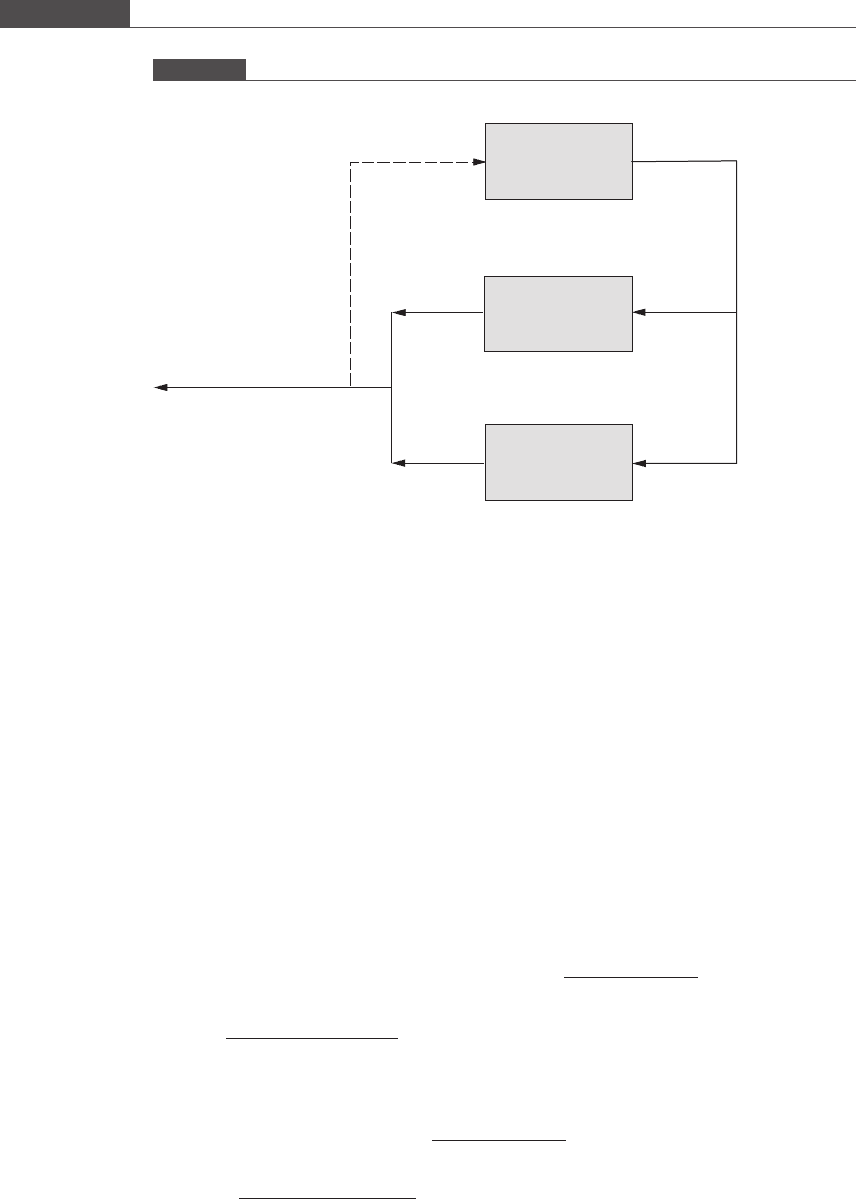
Routes of consumption of naphthalene epoxide:

(1) conversion of epoxide to naphthalene dihydrodiol;

(2) binding to GSH to form epoxide–GSH conjugates;

(3) rearrangement to naphthol.

The material balance diagram for naphthalene epoxide (NO) is shown in Figure

P2.1.

Since we are dealing with a multicomponent system, we use superscripts N, NO,

and NOH for naphthalene, naphthal ene epoxide, and naphthol, respectively, to

differentiate between the concentration terms in various compartments.

A mass balance of NO is performed over the two chambers – lung and liver. This

yields two linear equations in the unknowns C

lung

and C

liver

. Note that simpliﬁcations

have been made to the original equations (Quick and Shuler, 1999) by assuming that

lung

and C

liver

are small in comparison to relevant constants present in the equations.

Lung compartment

liver

þ Q

lung



þ v

max;P450-lung

lung



max;EH-lung

lung

m;EH-lung

lung

 V

lung

max;GST

lung

GSH

lung

þ K2

lung

GSH

lung

 k

NOH

exp l

NOH

lung



lung

 Q

lung

¼ 0

(P2:1)

Liver compa rtment

liver

lung

þ v

max;P450-liver

liver



max;EH-liver

liver

m;EH-liver

liver

 V

liver

max;GST

liver

GSH

liver

þ K2

liver

GSH

liver

 k

NOH

exp l

NOH

liver

ðÞC

liver

 Q

liver

¼ 0:

(P2:2)

Figure P2.1

Material balance diagram for naphthalene epoxide.

Other

tissues

Recycle stream

lung

(1 – R)(Q

liver

+ Q

), C

Additional material balance equations:

lung

= Q

liver

+ Q

NO NO NO

lung

out

= Q

liver

+ Q

lung

Well-mixed reactor

Lung

Purge stream

liver

, C

liver

R(Q

liver

+ Q

), C

out

, C

lung

, C

lung

liver

, C

liver

, C

lung

liver

Well-mixed reactor

Liver

129

2.14 Problems

NO balance assumptions

(1) Binding of naphthalene epoxide to proteins is comparatively less important and can

be neglected.

(2) The concentra tion of GSH in cells is constant. It is assumed that GSH is resynthe-

sized at the rate of consumption.

(3) Production of the RS enantiomer of the epoxide (compared to SR oxide) is domi-

nant, and hence reaction parameters pertaining to RS production only are used.

(4) The total protein content in the cells to which the metabolites bind remains fairly

constant.

The parametric values and deﬁnitions are provided below. The modeling param-

eters correspond to naphthalene processing in mice.

Flowrates

lung

: ﬂowrate through lung compartment = 2 μl/min;

liver

: ﬂowrate through liver compartment = 0.5 μl/min;

: ﬂowrate through other tissues compartment = 1.5 μl/min.

Compartment volumes

lung

: volume of lung compartment = 2 mm × 2mm× 20 μm=8× 10

8

l = 0.08μl;

liver

: volume of liver compartment = 3.5 mm × 4.6 mm × 20 μm = 3.22 × 10

7

= 0.322 μl.

Reaction constants

(1) Naphthalene → naphthalene epoxide

max,P450-lung

: maximum reaction velocity for conversion of naphthalene into

napthalene epoxide by cytochrome P450 monooxygenases in lung

cells = 8.75 μM/min;

max,P450-liver

: maximum reaction velocity for conversion of naphthalene into

napthalene epoxide by cytochrome P450 monooxygenases in liver

cells = 118 μM/min.

(2) Naphthalene epoxide → naphthalene dihydrodiol

max,EH-lung

: maximum reaction velocity for conversion of naphthalene epoxide to

dihydrodiol by epoxide hydrolase in the lung = 26.5 μM/min;

m,EH-lung

: Michaelis constant = 4.0 μM;

max,EH-liver

: maximum reaction velocity for conversion of naphthalene epoxide to

dihydrodiol by epoxide hydrolase in the liver = 336 μM/min;

m,EH-lung

: Michaelis constant = 21 μM

(3) Naphthalene epoxide → naphthol

NOH

: rate constant for rearrangement of epoxide to naphthol = 0.173 μM/μMof

NO/min;

NOH

: constant that relates naphthol formation rate to total protein content =

− 20.2 ml/g protein

(4) Naphthalene epoxide → epoxide–GSH conjugates

max,GST

: maximum reaction velocity for binding of naphthale ne epoxide to GSH

catalyzed by GST (glutathione S-transferase) = 2750 μM/min;

lung

: constant in epoxide–GSH binding rate = 310 000 μM

;

lung

: constant in epoxide–GSH binding rate = 35 μM;

liver

: constant in epoxide–GSH binding rate = 150 000 μM

;

liver

: constant in epoxide–GSH binding rate = 35 μM.

130

Systems of linear equations

Protein concentrations

lung

: total protein content in lung compartment = 92 mg/ml;

liver

: total protein content in liver compartment = 192 mg/ml;

GSH

lung

: GSH concentration in lung compartment = 1800 μM;

GSH

liver

: GSH concentration in liver compartment = 7500 μM;

R: fraction of the exiting stream that reenters the microcircuit.

Your goal is to vary the recycle fraction from 0.6 to 0.95 in increasing increments of

0.05 in order to study the effect of reduced excretion of toxicant on circulating

concentration values of naphthalene and its primary metabolite naphthalene epox-

ide. You will need to write a MATLAB pro gram to perform the following.

(a) Use the Gaussian elimination method to determine the napthalene epoxide

concentrations at the outlet of the lung and liver compartments of the animal-

on-a-chip for the range of R speciﬁed.

(b) Plot the concentration values of epoxide in the liver and lung chambers as a

function of R.

decomposition method. (You can use the MATLAB backslash operator to

perform the forward and backward substitutions.)

2.5. Pharmacokinetic modeling for “animal-on-a-chip” – 2 Repeat problem 2.4 for

naphthalene concentrations in lung and liver for recycle ratios 0.6 to 0.9. The

constants and relevant equations are given in Box 2.1.What happen s when we

increase R to 0.95? Why do you think this occurs? (Hint: Look at the assumptions

made in deriving the Michaelis–Menten equation.) Chapter 5 discusses solution

techniques for nonlinear equ ation sets. See Problem 5.10.

2.6. Pharmacokinetic modeling for “a nimal-on-a-chip” – 3

(a) Are the sets of equations dealt with in Problems 2.4 and 2.5 always well-

conditioned? What happens to the conditioning of the system of Equations (2.3)

and (2.4)asR →1? Calculate the condition numbers for the range of R speciﬁed.

(b) What happens to the nature of the solution of the two simultaneous linear

Equations (2.3) and (2.4) when R is exactly equal to one?

Figure P2.2

Banded matrix.

p sub-diagonals above main

diagonal are non-zero

Main diagonal

q sub-diagonals below main

dia

onal are non-zero

131

2.14 Problems

why not? If Equations (P2.1) and (P2.2) produce a solution even when R =1,

explain why the steady state assumption is still not valid.

2.7. LU decomposition of tridiagonal matrices In banded matrices, the non-zero

elements are located in a speciﬁc part of the matrix as shown in Figure P2.2. The

non-zero part of the matrix consists of a set of diagonals and includes the main

diagonal. Everywhere else, the matrix elements are all zero.

The bandwidth of a banded matrix is equal to p + q + 1, where

p is the number of non-zero sub-diagonals located above the main diagonal,

q is the number of non-zero sub-diagonals located below the main diagonal, an d

1 is added to include the main diagonal.

Large banded matrices are sparse matrices. The minimum number of operations

necessary to obtain a solution to a system of linear eq uations whose coefﬁcient

matrix is a large banded matrix is much less than the O(n

) number of operations

required by Gaussian elimination or LU decomposition.

Consider the tridiagonal matrix A:

A ¼

000 ... 0

00 ... 0

0 b

0 ... 0



 

0 ... 0 b

n1

0 ... 00 b

A is an example of a banded matrix. We seek an efﬁcient elimination method to

resolve a banded matrix to a triangular matrix.

A banded matrix has a convenient property. If LU decomposition is performed

on a banded matrix via the Doolittle method without pivoting, the resulting U and L

matrices have narrower bandwidths than the original matrix. A can be broken down

into the product of two triangular banded matrices as shown below:

A ¼ LU

100 0... 0

10 0... 0

0 β

10... 0

... 0 β

0 ... 0 β

00 ... 0

0 α

0 ... 0

00α

0 ... 0

0 ... 0 α

n1

0 ... 00 α

You are asked to perform matrix multiplications of L with U, and compare the result

with the corresponding elements of A. Show that

¼ a

; α

¼ a

 β

k1

; β

k1

; for 2  k  n

¼ c

; for 1  k  n:

132

Systems of linear equations

Note that the number of addition/subtraction, multiplication, and division oper-

ations involved in obtaining the elements of the L and U matrices is 3(n – 1). This

method is much more efﬁcient than the traditional O(n

) operations required by

standard Gaussian elimination for full matrices.

2.8. Thomas method for tridiagonal matrices Tridiagonal matrices are commonly

encountered in many engineering and science applications. Large tridiagonal matri-

ces have many zero elements. Standard methods of solution for linear systems are

not well-suited for handling tridiagonal matrices since use of these methods entails

many wasteful operations such as addition and multiplication with zeros. Special

algorithms have been formulated to handle tridiagonal matrices efﬁciently. The

Thomas method is a Gaussian elimination procedure tailored speciﬁcally for tri-

diagonal systems of equations as shown below:

Ax ¼

000

0 l

00l

000l

¼ b

The Thomas algorithm converts the tridiagonal matrix into a upper triangular

matrix with ones along the main diagonal. In this method, the three diagonals

containing non-zero elements are stored as three vectors, d, l,andu, where

d is the main diagonal;

l is the sub-diagonal immediately below the main diagonal; and

u is the sub-diagonal immediately above the main diagonal.

The Thomas method is illustrated below by performing matrix manipul ations on

a full matrix. Keep in mind that the operations are actually carried out on a set of

vectors.

Step 1 The top row of the augmented matrix is divided by d

to convert the ﬁrst

element in this row to 1. Accordingly,

; b

Step 2 The top row is multiplied by l

and subtracted from the second row to

eliminate l

. The other non-zero elements in the second row are modiﬁed

accordingly as

¼ d

 l

; b

¼ b

 l

The augmented matrix becomes

augA ¼

1 u

000: b

0 d

00: b

0 l

0 : b

00l

: b

00 0 l

: b

133

2.14 Problems

Step 3 The secon d row is divided by d

to make the new pivot element 1. Thus, the

non-zero elements in the second row are again modiﬁed as follows:

 l

; b

 l

The augmented matrix is now

augA ¼

1 u

000: b

01u

00: b

0 l

0 : b

00l

: b

00 0 l

: b

Steps 2 and 3 are repeated for all subsequent rows i =3, ..., n. The only elemen ts

that need to be calculated at each step are u

and b

. Therefore, for all remaining rows,

 l

i1

; b

 l

i1

 l

i1

For the nth row, only b

needs to be calculated, since u

does not exist. The solution is

recovered using back substitution.

Write a MATLAB code to implement the Thomas method of solution for tri-

diagonal systems. Use the diag function to extract the matrix diagonals. Remember

that the vector l must have length n in order to use the mathematical relationships

presented here.

2.9. Countercurrent liquid extraction of an antibiotic Product recovery operations

downstream of a fermentation or enzymatic process are necessary to concentrate

and purify the product. The fermentation broth leaving the bioreactor is ﬁrst ﬁltered

to remove suspended particles. The aqueous ﬁltrate containing the product undergoes

a number of separation operations such as solvent extraction, adsorption, chroma-

tography, ultraﬁltration, centrifugation, and crystallization (Bailey and Ollis, 1986).

In the liquid extraction process, the feed stream containing the solute of interest is

contacted with an immiscible solvent. The solvent has some afﬁnity for the solute, and,

during contacting between the two liquid streams, the solute distributes between the

two phases. The exiting solvent stream enriched in solute is called the extract.The

residual liquid from which the desired component has been extracted is called the

rafﬁnate. A single liquid–liquid contact operation is called a stage.Ideally,duringa

stagewise contact the distribution of the solute between the two liquids reaches

equilibrium. A stage that achieves maximum separation as dictated by equilibrium

conditions is called a theoretical stage. A scheme of repeated contacting of two

immiscible liquid streams to improve separation is called a multistage process. An

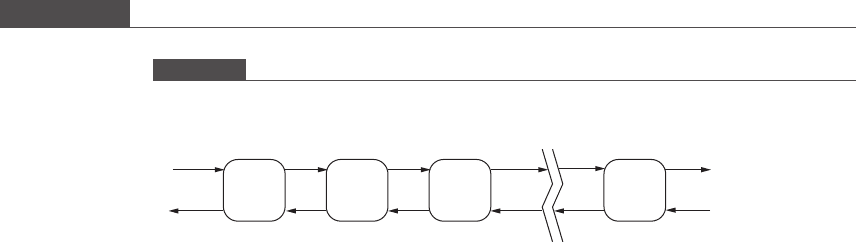
example of this is multistage countercurrent extraction. Figure P2.3 shows a schematic

of a countercurrent extractor that contains n stages. The concentration of solute in the

entering feed stream is denoted by x

or x

n+1

, and that in the entering solvent stream is

denoted by y

or y

. We simplify the analysis by assuming that the mass ﬂowrates of

the liquid streams change very little at each stage. If the rafﬁnate stream dissolves

signiﬁcant quantities of solvent, or vice versa, then this assumption is invalid. A mass

balance performed on any stage i =2, ..., n – 1 under steady state operation yields

134

Systems of linear equations

þ Fx

¼ Sy

i1

þ Fx

iþ1

: (P2:3)

The equilibrium distribution between the two phases is speciﬁed by the distribution

coefﬁcient,

K ¼ y= x: (P2:4)

Combining Equations (P2.3) and (P2.4), we get

SKx

þ Fx

¼ SKx

i1

þ Fx

iþ1

Rearranging, the above expression becomes

SKx

i1

 SK þ FðÞx

þ Fx

iþ1

¼ 0:

We are interested in determining the concentration of the solute (product) in the

ﬁnal extract and in the exiting rafﬁnate. For this purpose a mass balance is performed

on each of the n stages. The set of simultaneous linear equations can be expressed in

matrix form Ax = b , where

A ¼

ðSK þ FÞ F 00... 0

SK ðSK þ FÞ F 0 ... 0

0 SK ðSK þ FÞ F ... 0

0 ... 00SK ðSK þ FÞ

;

x ¼

; and b ¼

Sy

Fx

A countercurrent solvent extraction of penicillin from broth ﬁltrate uses the

organic solvent amyl acetat e, and is deﬁned by the following process parameters:

F = 280 kg/hr,

S = 130 kg/hr,

= 0.035 kg penicillin/kg broth,

Figure P2.3

Countercurrent liquid extraction.

F, x

Stage

S, y

n–1

Feed stream

Solvent stream

Extract

Raffinate

Stage

S, y

F, x

135

2.14 Problems

= 0, and

K = 2.0.

It is desired that the ﬁnal concentration of penicillin in the rafﬁnate be x

0.005 kg penicillin/kg broth. How many stages are required? Use the MATLAB

program that you developed in Problem 2.8 to solve tridiagonal matrix equations.

Start with a guess value of n = 3, and increase n in steps of one until the desired value

of x

is achieved. You will need to create new A and b for each n considered. You can

use the MATLAB function diag to create three diagonal matrices from three

vectors and sum them up to obtain A. Draw a plot in MATLAB of the exiting

pencillin concentration versus the number of theoretical stages requ ired to achieve

the corresponding separation.

Linear regression

2.10. If a straight line

¼ β

þ β

(P2:5)

is ﬁtted to a data set (x, y), then the intercept is given by Equation (2.38) (repeated

here) as



y  β



x: (2:38)

If we substitute β

in Equation (P2.5) with the expression given by Equation (2.38),

we obtain





y ¼ β





xðÞ: (P2:6)

Using Equation (P2.6), show that the point ð



yÞlies on a straight line obtained by

regression of y on x.

2.11. Use Equation (P2.6) to show that the sum of the residuals obtained from a least-

squares regression of y on x is equal to zero, i.e.

i¼1



¼ 0: (P2:7)

Use Equation (P2.7) to show that the average of

is equal to the mean of y

2.12. Power-law prediction of animal metabolism Find a power-law relationship

between an animal’s mass and its metabolism. Table P2.1 gives animals’ masses in

kilograms and metabolism rates in kilocalories per day (Schmidt-Nielsen, 1972 ).

You will need to take the natural log of both the independent and dependent

variables to determine the power-law exponent and coefﬁcient (i.e. log (metabolic

Table P2.1.

Animal Mass (kg) Metabolism (kcal/day)

Horse 700 11 760

Human 70 1700

Sheep 55 1450

Cat 15 720

Rat 0.4 30

136

Systems of linear equations