King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

elimination for square n × n matrices. MATLAB assesses the structural properties of

A before deciding which algorithm to use for solving A \ b.IfA is a triangular matrix,

then backward or forward substitution is applied directly to obtain x.IfA is singular

or nearly singular, MATLAB issues a warning message so that the result produced

may be interpreted by the user accordingly. The function mldivide executes the

left-division operation that is represented by the \ operator. Type help mldivide

for more information on the backslash operator.

We use the backslash operator to solve Equations (E1)–(E3):

A=[2−43;12−3; 3 1 1];

b = [1; 4; 12];

x = A\b

The output produced is

The backslash operator is capable of handling overdetermined and underdeter-

mined systems as well, e.g. systems described by a rectangular m × n matrix A.

2.7 Ill-conditioned problems and the condition number

One may encounter a system of equations whose solution is considerably sensitive to

slight variations in the values of any of the coefﬁcients or constants. Such systems exhibit

large ﬂuctuations in the solutions despite comparatively small changes in the parametric

values. Any solution of these equations is usually not reliable or useful since it is often far

removed from the true solution. Such systems of equations are said to be ill-conditioned.

Often coefﬁcient values or constants of equations are derived from results of experi-

ments or from estimations using empirical equations and are only approximations to the

true values. Even if the problem at hand contains an approximate set of equations, we

wish the solution to be as close as possible to the true solution corresponding to the set of

equations having the correct coefﬁcients and constants. Equations that show little

variability in the solution despite modest changes in the parameters are said to be

well-conditioned. Even in cases where the coefﬁcients and constants of the equations

are known exactly, when performing numerical computations ﬁnite precision will

introduce round-off errors that will perturb the true value of the parameters. Such

small but ﬁnite perturbations will produce little change in the solutions of well-

conditioned problems, but can dramatically alter the result when solving ill-conditioned

systems of equations. Therefore, when working with ill-conditioned problems, or with

problems involving numbers of disparate magnitudes, it is always recommended to

carry out numerical computations in double precision, since powerful computational

resources – high speeds and large memory – are easily available.

Ill-conditioning is an inherent property of the system of equations and cannot be

changed by using a different solution algorithm or by using superior solution

techniques such as scaling and pivoting. The value of the determinant of the

coefﬁcient matrix indicates the conditioning of a system of linear equations. A set

of equations with a coefﬁcient matrix determinant close to zero will always be ill-

conditioned. The effect of the conditioning of the coefﬁcient matrix on the solution

outcome is demonstrated below.

2.7 Ill-conditioned problems and the condition number

Example 2.6

Let’s consider a 2 × 2 well-conditioned coefficient matrix and 2 × 1 constants vector:

A=[23;41];

b = [5; 5];

x = A\b

Now let’s change the constants vector to

bnew = [5.001; 5];

xnew = A\bnew

xnew =

0.9999

1.0004

The relative change in the first element of b = 0.001/5 = 0.0002. The relative change in the solutions is

calculated as 0.0001 and 0.0004 for both unknowns, which is of the same order of magnitude as the slight

perturbation made to the constants vector. This is representative of the behavior of well-conditioned

coefficient matrices.

Now let’s study the behavior of an ill-conditioned coefficient matrix:

A = [4 2; 2.001 1];

b = [6; 3.001];

x = A\b

1.0000

The answer is correct. Let’s introduce a slight modification in the first element of b:

bnew = [6.001; 3.001];

xnew = A\bnew

xnew =

0.5000

2.0005

A relative perturbation of 0.001/6 = 0.000167 (0.0167%) in only one of the elements of b resulted in a

relative change of 0.5 (50%) and 1.0005 (100%) in the magnitudes of the two variables. The changes

observed in the resulting solution are approximately 3000–6000 times the original change made in the first

element of b!

Next, we calculate how well xnew satisfies the original system of equations (b = [6; 3.001]). To

determine this, we calculate the residual (see Section 2.9 for a discussion on “residuals”), which is

defined as krk¼kb  Axk. The residual is an indicator of how well the left-hand side equates to the

right-hand side of the equations, or, in other words, how well the solution x satisfies the set of equations:

r=b– A*xnew

−0.0010

The solution

to the perturbed set of equations satisfies the original system of equations well, though not

exactly. Clearly, working with ill-conditioned equations is most troublesome since numerous solutions of

a range of magnitudes may satisfy the equation within tolerable error, yet the true solution may remain

elusive.

Systems of linear equations

In ord er to understand the origin of ill-conditioning, we ask the following question:

how is the magnitude of the slight perturbations in the constants in b or the

coefﬁcients in A related to the resulting change in the solution of the equations?

Consider ﬁrst small variations occurring in the individ ual elements of b only.

Consider the original equation Ax = b. Let Δb be a small change made to b, such

that the solution changes by Δx. The new system of equations is given by

Axþ ΔxðÞ¼b þ Δb:

Subtracting off Ax = b, we obtain

AΔx ¼ Δb

Δx ¼ A

1

Δb:

Taking the norms of both sides yields

kΔxk¼kA

1

ΔbkkA

1

kkΔbk: (2:21)

Now we take the norm of the original equation Ax ¼ b to obtain

kbk¼kAxkkAkkxk

kAkkxk



kbk

: (2:22)

Mutliplying Equation (2.21) with (2.22), we obtain

kΔxk

kAkkxk



1

kkΔbk

kbk

Rearranging,

kΔxk

kxk

kAkkA

1

kΔbk

kbk

: (2:23)

Here, we have a relationship between the relative change in the solution and the

relative change in b. Note that kΔxk=kxk is dependent on two factors:

(1) kΔbk=kbk, and

(2) kAkkA

1

The latter term deﬁnes the condition number, and is denoted as cond(A). The condition

number is a measure of the conditioning of a system of linear equations. The minimum

value that a condition number can have is one. This can be proven as follows:

kA  A

1

k¼kIk¼1:

Now,

kA  A

1

kkAkkA

1

k¼condðAÞ:

Thus,

condðAÞ1:

The condition number can take on values from one to inﬁnity. A well-conditioned

matrix will have low condition numbers close to one, while large condition numbers

2.7 Ill-conditioned problems and the condition number

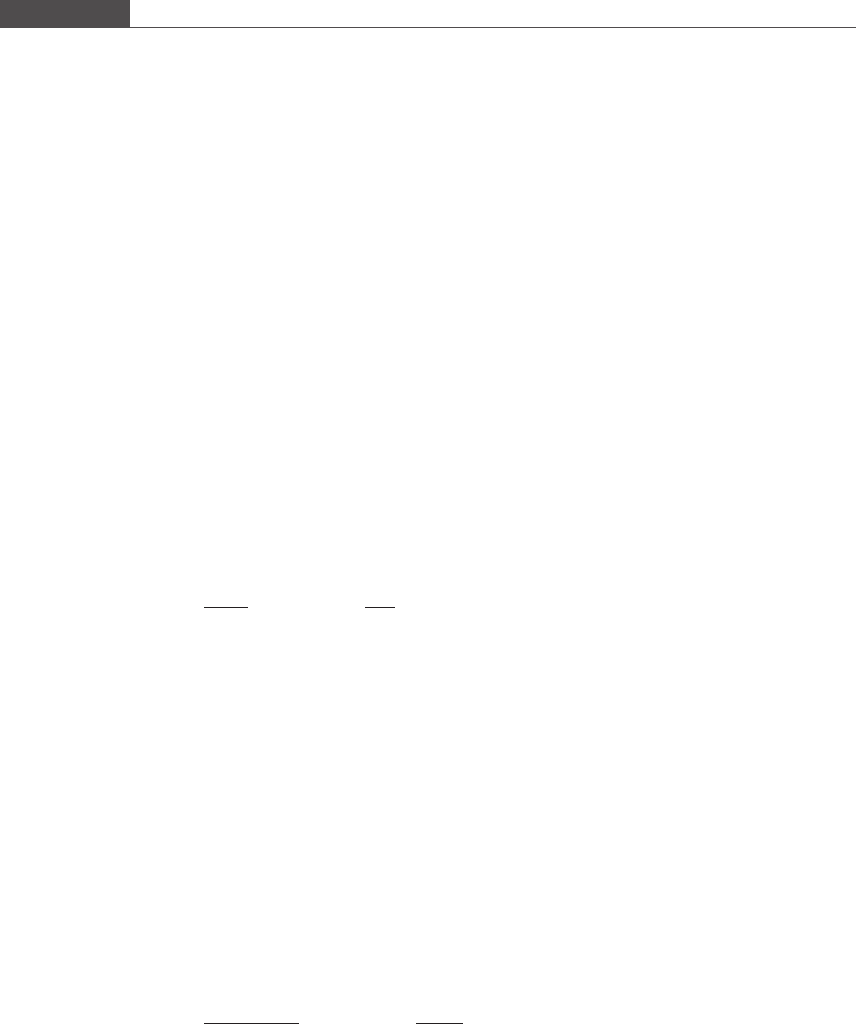
indicate an ill-conditioned problem. The error in the solution kΔxk=kxk will be of the

order of kΔbk=kbk, only if cond(A)isofO(1). Knowledge of the condition number of a

system enables one to interpret the accuracy of the solution to a perturbed system of

equations. The exact value of the condition number depends on the type of norm used

(p =1,2,or∞), but ill-conditioning will be evident regardless of the type of norm.

A ﬁxed cut-off condition number that deﬁnes an ill-conditioned system does not exist

partly because the ability to resolve an ill-conditioned problem is dependent on the

level of precision used to perform the arithmetic operations. It is always recommended

that you calculate the condition number when solving systems of equations.

The goal of the Gaussian elimination method of solution (and LU decomposition

method) is to minimize the residual krk¼kb  Axk. When numerical procedures are

carried out, round-off errors creep in and can corrupt the calculated values. Such

errors are carried forward to the ﬁnal solution. If x + Δx is the numerically

calculated solution to the system of equations Ax = b, and x is the exact solution

to Ax = b, then the residual is given by

r ¼ b  AxþΔxðÞ¼AΔx

kΔxk¼kA

1

rkkA

1

kkrk: (2:24)

Multiplying Equation (2.22) by Equation (2.24) and rearranging, we arrive at

kΔxk

kxk

kAkkA

1

krk

kbk

: (2:25)

The magnitude of error in the solution obtained using the Gaussian elimination

method also depends on the condition number of the coefﬁcient matrix.

Let’s look now at the effect of perturbing the coefﬁcient matrix A.Ifx is the exact

solution to Ax = b, and perturbations of magnitude ΔA change the solution x by an

amount Δx, then our corresponding matrix equation is given by

A þ ΔAðÞx þ ΔxðÞ¼b:

After some rearrangement,

Δx ¼A

1

ΔAxþ ΔxðÞ:

Taking norms,

kΔxkkA

1

kkΔAkk x þ ΔxðÞk:

Multiplying and dividing the right-hand side by kAk, we obtain

kΔxk

k x þ ΔxðÞk

kA

1

kkAk

kΔAk

kAk

: (2:26)

Again we observe that the magnitude of error in the solution that results from

modiﬁcation to the elements of A is dependent on the condition number. Note

that the left-hand side denominator is the solution to the perturbed set of equations.

Using MATLAB

MATLAB provides the cond function to calculate the condition number of a matrix

using either the 1, 2, or ∞ norms (the default norm that MATLAB uses is p = 2).

100

Systems of linear equations

Let’s use this function to calculate the condition numbers of the coefﬁcient matrices

in Example 2.6:

A=[23;41];

C1 = cond(A,1)

C1 =

Cinf = cond(A,inf)

Cinf =

3.0000

A = [4 2; 2.001 1];

C1 = cond(A,1)

C1 =

1.8003e+004

Cinf = cond(A,inf)

Cinf =

1.8003e+004

The calcul ation of the condition number involv es determining the inverse of the

matrix which requires O(n

) ﬂoating-point operations or ﬂops. Calculating A

−1

is an

inefﬁcient way to determine cond(A), and computers use specially devised O(n

)

algorithms to estimate the condition number.

2.8 Linear regression

Experimental observations from laboratories, pilot-plant studies, mathematical modeling

of natural phenomena, and outdoor ﬁeld studies provide us with a host of biomedical,

biological, and engineering data, which often specify a variable of interest that exhibits

certain trends in behavior as a result of its dependency on another variable. Finding a “best-

ﬁt” function that reasonably ﬁts the given data is valuable. In some cases, an established

theory provides a functional relationship between the dependent and independent varia-

bles. In other cases, when a guiding theory is lacking, the data itself may suggest a functional

form for the relationship. Sometimes, we may wish to use simple or uncomplicated

functions, such as a linear or quadratic equation to represent the data, as advised by

Ockham’s (Occam’s) razor – a heuristic principle posited byWilliamOckham, a fourteenth

century logician. Occam’s razor dictates the use of economy and simplicity when develop-

ing scientiﬁc theories and explanations and the elimination of superﬂuous or “non-key”

assumptions that make little difference to the characteristics of the observed phenomena.

The technique used to derive an empirical relationship between two or more varia-

bles based on data obtained from experimental observations is called regression.The

purpose of any regression analysis is to determine the parameters or coefﬁcients of the

function that best relate the dependent variable to one or more independent variables. A

regression of the data to a “best-ﬁt” curve produces a function that only approximates

the given data to within a certain degree, but does not usually predict the exact values

speciﬁed by the data. Experimentally obtained data contain not only inherent errors

due to inaccuracies in measurements and underlying assumptions, but also inherent

variability or randomness that is characteristic of all natural processes (see Section 3.1

for a discussion on “variability in nature and biology”). Hence, it is desirable to obtain

an approximate function that agrees with the data in an overall fashion rather than

forcing the function to pass through every experiment ally derived data point since the

exact magnitude of error in the data is usually unknown. The parameters of the ﬁtted

curve are adjusted according to an error minimization criterion to produce a best-ﬁt.

101

2.8 Linear regression

Linear regression models involve a strict linear dependency of the functional form

on the parameters to be determined. For example, if y depends on the value of x, the

independent variable, then a linear regression problem is set up as

y ¼ β

xðÞþβ

xð Þþþβ

xðÞ;

where f can be any function of x,andβ

, β

, ..., β

are constants of the equation that

are to be determined using a suitable regression technique. Note that the ind ividual

functions f

(x)(1≤ i ≤ n) may depend nonlinearly on x, but the unknown parameter

must be separable from the functional form speciﬁed by f

(x). The linear least-

squares method of regression is a popul ar curve-ﬁtting method used to approximate a

line or a curve to the given data. The functional relationship of the dependent

variable on one or more independent variables can be linear, exponential, quadratic,

cubic, or any other nonlinear dependency.

In any linear regression problem, the number of linear equations m is greater than

the number of coefﬁcients n whose values we seek. As a result, the problem most

often constitutes an overdetermined system of linear equations, i.e. a set of equations

whose coefﬁcient matrix has a rank equal to the number of columns n, but unequal

to the rank of the augmented matrix, which is equal to n + 1, resulting in incon-

sistency of the equation set and therefore the lack of an exact solution. Given a

functional form that relates the variables under consideration, the principle of the

least-squares method is to minimize the error or “scatter” of the data points about

the ﬁtted curve. Before proceeding, let’s consider a few examples of biomedical

problems that can be solved using linear regression techniques.

Box 2.2A Using hemoglobin as a blood substitute: hemoglobin–oxygen binding

Hemoglobin (Hb) is a protein present in red blood cells that is responsible for the transport of oxygen

) from lungs to individual tissues throughout the body and removal of carbon dioxide (CO

) from the

tissue spaces for transport to the lungs. The hemoglobin molecule is a tetramer and consists of four

subunits, two α chains, and two β chains. Each α or β polypeptide chain contains a single iron atom-

containing heme group that can bind to one O

molecule. Thus, a hemoglobin molecule can bind up to

four O

molecules. The subunits work cooperatively with each other (allosteric binding), such that the

binding of one O

molecule to one of the four subunits produces a conformational change within the

protein that makes O

binding to the other subunits more favorable. The binding equation between

hemoglobin and oxygen is as follows:

HbðO

$ Hb þ nO

;

where n =1, ...,4.

The exchange of O

and CO

gases between the lungs and tissue spaces via the blood occurs due to

prevailing differences in the partial pressures of pO

and pCO

, respectively. The atmospheric air

contains 21% O

. The O

in inspired air exerts a partial pressure of 158 mm Hg (millimeters of mercury),

which then reduces to 100 mm Hg when the inspired air mixes with the alveolar air, which is rich in CO

Venous blood that contacts the alveoli contains O

at a partial pressure of 40 mm Hg. The large

difference in partial pressure drives diffusion of O

across the alveolar membranes into blood. Most of

the oxygen in blood enters into the red blood cells and binds to hemoglobin molecules to form

oxyhemoglobin. The oxygenated blood travels to various parts of the body and releases oxygen from

oxyhemoglobin. The partial pressure of oxygen in the tissue spaces depends on the activity level of the

tissues and is lower in more active tissues. The high levels of CO

in the surrounding tissue drive entry

of CO

into blood and subsequent reactions with water to produce bicarbonates (HCO

−

). Some of the

bicarbonates enter the red blood cells and bind to hemoglobin to form carbaminohemoglobin. At the

lungs, the oxygenation of blood is responsible for the transformation of carbaminohemoglobin to

102

Systems of linear equations

oxyhemoglobin or the dissociation of CO

from hemoglobin, and conversion of bicarbonates into CO

and H

O, resulting in CO

leaving the blood and entering into the lungs.

The Hill equation describes a mathematical relationship between the extent of oxygen saturation of

hemoglobin and the partial pressure of O

in blood. This equation is derived from the application of the

law of mass action to the state of chemical equilibrium of the reaction

HbðO

$ Hb þ nO

;

S ¼

HbðO



HbðO



þ Hb½

ðÞ

þ pO

ðÞ

: (2:27)

Equation (2.27) is the Hill equation, and accounts for the observed cooperative binding that

produces the characteristic sigmoidal shape of the hemoglobin–oxygen dissociation curve.

The partial pressure of oxygen that results in occupancy of half of the oxygen binding sites of

hemoglobin is denoted by P

Biochemical engineers at several universities have explored the use of polymerized bovine hemo-

globin as a possible blood substitute (Levy et al., 2002). Monomeric hemoglobin is small enough to

leak out of capillary pores; however, by chemically attaching several hemoglobin units together, the end

product is large enough to be retained within the circulatory system. Data collected for tetrameric bovine

hemoglobin binding to oxygen are given in Table 2.1.

We first examine the shape of the oxygen dissociation curve by plotting the data in Figure 2.5.

We wish to determine the best-fit values of P

and n in the Hill equation for this data set and

compare with values measured for human hemoglobin. Equation (2.27) is nonlinear but can be

converted to linear form by first rearranging to

Figure 2.5

A plot of the fractional saturation of hemoglobin S as a function of the partial pressure of oxygen in plasma.

0 20 40 60 80 100 120

0.2

0.4

0.6

0.8

(mm Hg)

Hemoglobin−oxygen dissociation curve

Table 2.1. Fractional saturation of hemoglobin as a function of partial pressure of

oxygen in blood

(mm Hg)

10 20 30 40 50 60 70 80 90 100 110 120

S 0.18 0.40 0.65 0.80 0.87 0.92 0.94 0.95 0.95 0.96 0.96 0.97

103

2.8 Linear regression

1  S

ðpO

and then taking the logarithm of both sides to obtain

1  S

¼ n ln pO

ðÞn ln P

: (2:28)

Plotting lnðS=1  SÞ as a function of ln pO

ðÞproduces a line with slope n and intercept n ln P

Equation (2.28) is the functional form for the dependency of oxygen saturation of hemoglobin as a

function of the oxygen par tial pressure, and is linear in the regression parameters.

We will be in a position to evaluate the data once we learn how to fit the line described by Equation

(2.28) to the data presented above.

Box 2.3A Time course of drug concentration in the body

Drugs can be delivered into the body by many different routes, a few examples of which are ingestion of

drug and subsequent absorption into blood via the gastrointestinal tract, inhalation, topical application

on the skin, subcutaneous penetration, and intravenous injection of drug directly into the circulatory

system. The rate at which the drug enters into the vascular system, the extravascular space, and/or

subsequently into cells, depends on a variety of factors, namely the mode of introduction of the drug into

the body, resistance to mass transfer based on the chemical properties of the drug and iner t material

(such as capsules) associated with the drug, and the barriers offered by the body’s interior. Once the

drug enters into the blood, it is transported to all parts of the body and may enter into the tissue spaces

surrounding the capillaries. The amount of drug that succeeds in entering into the extravascular space

depends on the resistance faced by the drug while diffusing across the capillary membranes. While the

active form of the drug distributes throughout the body, it is simultaneously removed from the body or

chemically decomposed and rendered inactive either by liver metabolism, removal by kidney filtration,

excretion of feces, exhalation of air, and/or perspiration. Thus, a number of processes govern the time-

dependent concentrations of the drug in blood and various parts of the body. The study of the processes

by which drugs are absorbed in, distributed in, metabolized by, and eliminated from the body is called

pharmacokinetics, and is a branch of the field of pharmacology. In other words, pharmacokinetics is

the study of how the body affects the transport and efficacy of the drug. A parallel field of study called

pharmacodynamics, which is another branch of pharmacology, deals with the time course of action

and effect of drugs on the body.

Pharmacokinetic studies of drug distribution and elimination aim at developing mathematical

models that predict concentration profiles of a particular drug as a function of time. A simplified

model of the time-dependent concentration of a drug that is injected all at once (bolus injection) and is

cleared from the blood by one or more elimination processes is given by

ðÞ

¼ C

kt

; (2:29)

where C

is the initial well-mixed blood plasma concentration of the drug immediately following

intravenous injection and is calculated as C

¼ D=V

app

, where D is the dosage and V

app

is the apparent

distribution volume. Note that k is the elimination rate constant with units of time

−1

and is equal to the

volumetric flowrate of plasma that is completely cleared of drug, per unit of the distribution volume of

the drug in the body.

Voriconazole is a drug manufactured by Pfizer used to treat invasive fungal infections generally

observed in patients with compromised immune systems. The use of this drug to treat fungal

endophthalmitis is currently being explored. Shen et al.(2007) studied the clearance of this drug

following injection into the vitreous humor (also known as “the vitreous”) of the eyes of rabbits. The

vitreous is a stagnant clear gel situated between the lens and the retina of the eyeball. The rate of

104

Systems of linear equations

exchange of compounds between the vitreous and the systemic circulation is very slow. The aqueous

humor is contained between the lens and the cornea and is continuously produced and drained from the

eye at an equal rate.

The time-dependent concentration of Voriconazole in the vitreous and aqueous humor is given in

Table 2.2 following intravitreal injection (Shen et al., 2007).

We use Equation (2.29) to model the clearance of the drug from rabbit eyes following a bolus

injection of the drug. If we take the logarithm of both sides of the equation, we get

ln CtðÞ¼ln C

 kt: (2:30)

Equation (2.30) is linear when ln C(t) is plotted against t, and has slope −k and intercept equal to

ln C

We want to determine the following:

(a) the initial concentration C

(b) the elimination rate constant k,

(d) the drug clearance rate from the vitreous of the eye relative to the clearance rate of drug from the

aqueous fluid surrounding the eye.

Table 2.2. Time-dependent concentrations of a drug called Voriconazole

in the vitreous and aqueous humor of rabbit eyes following intravitreal

bolus injection of the drug

Time, t (hr)

Vitreous concentration,

(t)(μg/ml)

Aqueous concentration,

(t)(μg/ml)

1 18.912 ± 2.058 0.240 ± 0.051

2 13.702 ± 1.519 0.187 ± 0.066

4 7.406 ± 1.783 0.127 ± 0.008

8 2.351 ± 0.680 0.000 ± 0.000

16 0.292 ± 0.090 0.000 ± 0.000

24 0.000 ± 0.000 0.000 ± 0.000

48 0.000 ± 0.000 0.000 ± 0.000

Box 2.4A Platelet flow rheology

A computational three-dimensional numerical model called “multiparticle adhesive dynamics” (MAD)

uses state-of-the-art fluid mechanical theory to predict the nature of flow of blood cells (e.g. white blood

cells and platelets) in a blood vessel (King and Hammer, 2001). White blood cells play an indispen-

sable role in the inflammatory response and the immune system, and one of their main roles is to search

for and destroy harmful foreign molecules that have entered the body. Platelets patrol the blood vessel

wall for lesions. They aggregate to form clots to curtail blood loss and promote healing at injured sites.

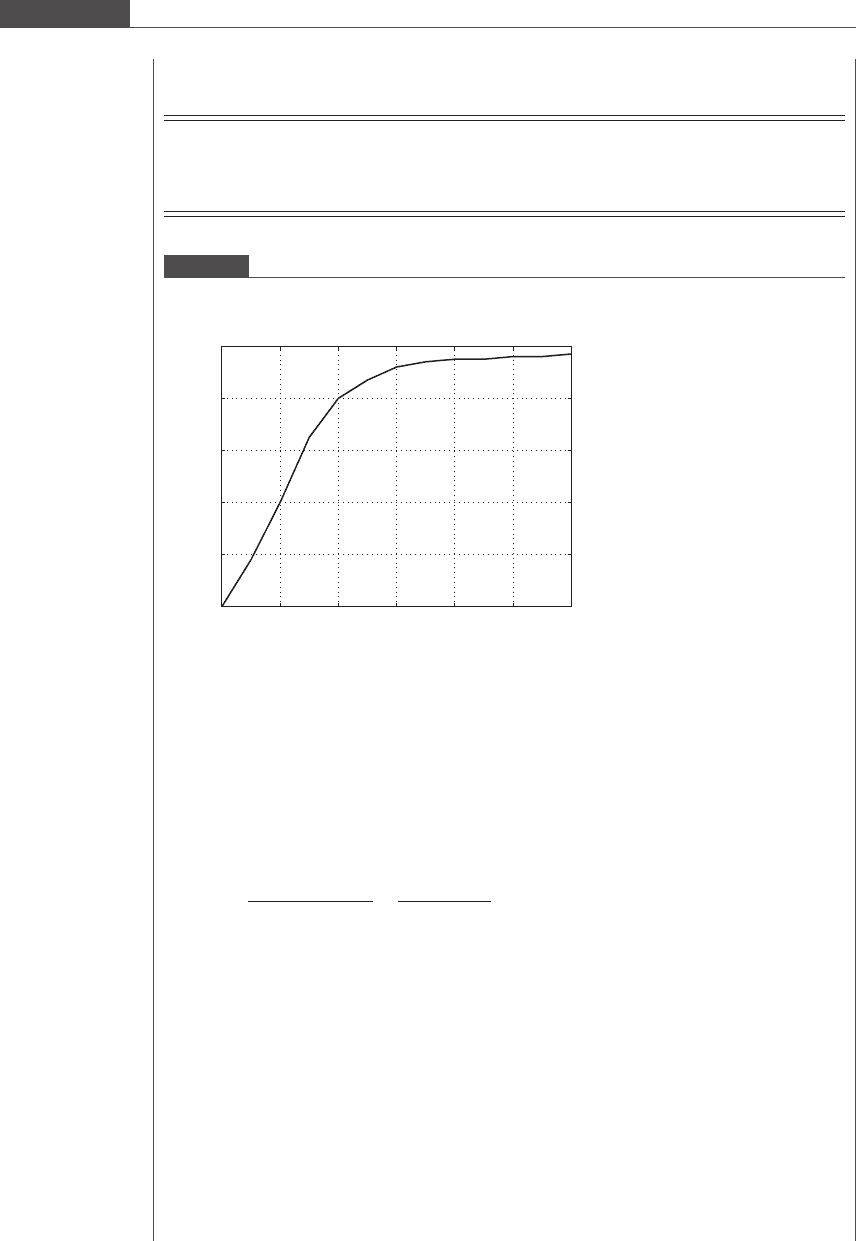
The flow behavior of a platelet-shaped cell (flattened ellipsoid) is dramatically different from that of a

spherical-shaped cell (Mody and King, 2005). It was determined from MAD studies that platelets flowing

in linear shear flow demonstrate three distinct regimes of flow near a plane wall. Platelets of dimension

2 × 2 × 0.5 μm

(see Figure 2.6) are observed to rotate periodically while moving in the direction of flow

at flow distances greater than 0.75 μm from the wall. Platelets at these heights also contact the surface at

regular intervals. When the platelet centroid height is less than 0.75 μm, the platelet cell simply glides or

cruises over the surface in the direction of flow without rotating, and does not contact the wall.

105

2.8 Linear regression

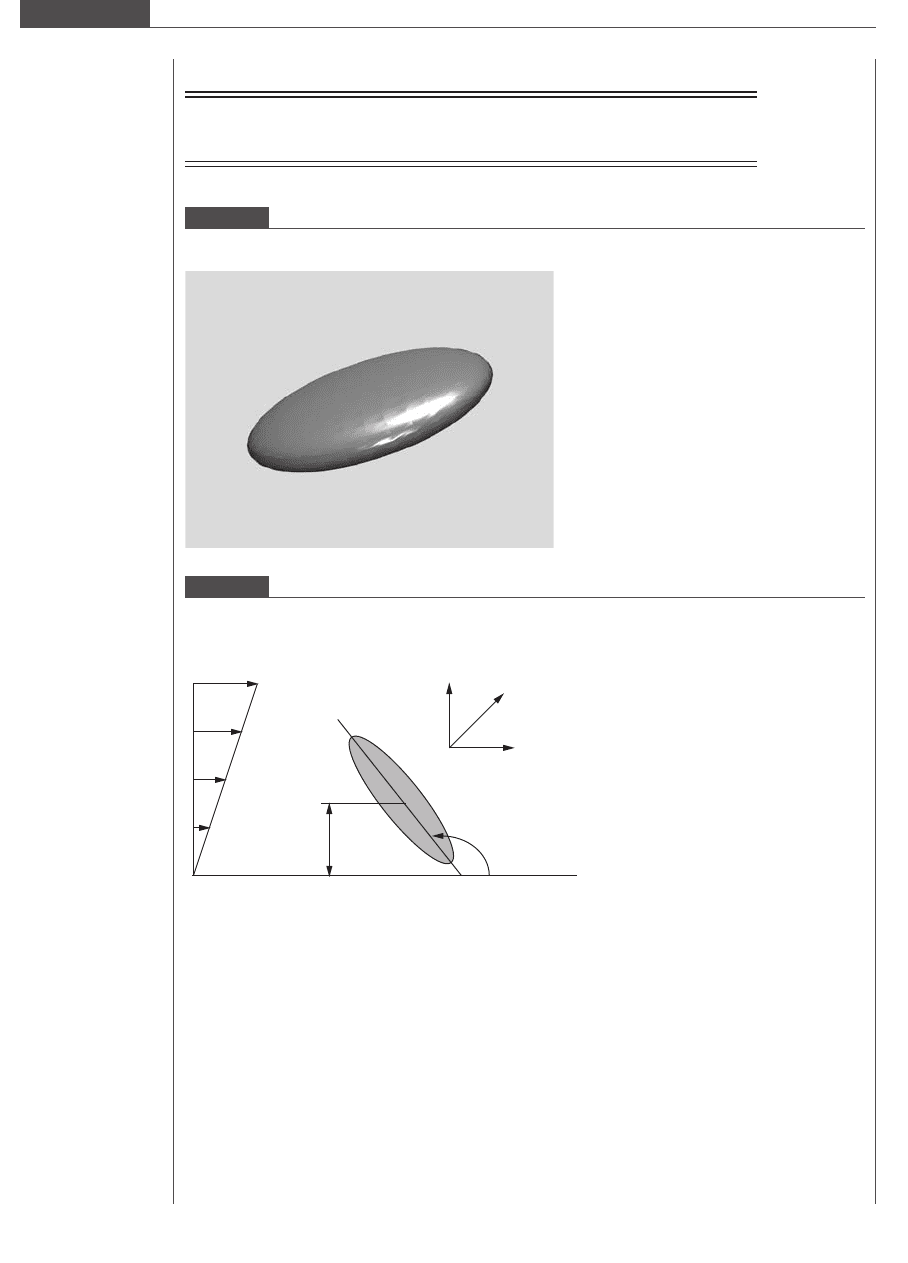
If a platelet flowing near a wall is subjected to linear shear flow, the relevant flow geometry is

depicted in Figure 2.7.

A platelet-shaped cell dramatically changes its flow behavior from a non-tumbling, non-wall-

contacting regime to a tumbling, wall-contacting flow regime under specific conditions of initial cell

orientation and distance of cell from the vessel wall (Mody and King, 2005). The starting orientation of a

platelet that forces a qualitative change in motion depends on the platelet proximity to the wall. The

initial platelet orientations α that produce a regime shift are given in Table 2.3 as a function of the platelet

height H from the surface and plotted in Figure 2.8.

If we wish to relate the initial orientation angle of the platelet α that produces a regime change with

initial platelet height H using a quadratic function, we require only three equations to determine the three

unknown parameters. The data in Table 2.3 contain five sets of (H, α) data points. Linear regression must

be employed to obtain a quadratic function that relates the dependency of α on H as prescribed by these

five data points.

Figure 2.6

Three-dimensional view of a simulated platelet-shaped cell of dimension 2 × 2 × 0.5 μm

Figure 2.7

Platelet modeled as an oblate spheroid (flattened ellipsoid) that is flowing (translating and rotating) in linear shear

flow over an infinite planar surface.

Linear shear flow

Platelet major axis

Table 2.3.

Initial tilt α (degrees) 10.5 10.0 8.5 7 4.5

Height H (μm) 0.50 0.55 0.60 0.65 0.70

106

Systems of linear equations