King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

H = [0.5; 0.55; 0.6; 0.65; 0.7];

A = [H.^2 H ones(size(H))];

alpha = [10.5; 10.0; 8.5; 7.0; 4.5];

c=(A’*A)\(A’*alpha)

MATLAB outputs

−114.2857

107.1429

−14.4714

Now we determine the coefficient of determination:

alphabar = mean(alpha)

alphabar =

8.1000

alphahat = polyval(c,H)

alphahat =

10.5286

9.8857

8.6714

6.8857

4.5286

SSR = sum((alpha-alphahat).^2)

SSR =

0.0571

R2 = 1 – SSR/sum((alpha-alphabar).^2)

R2 =

0.9976

This value of R

tells us that the quadratic fit accounts for 99.76% of the variation in the data. The

remaining 0.34% is assumed to be due to errors in obtaining the data, inherent variability in the data, or

due to higher-order dependencies. The fitted quadratic curve is plotted in Figure 2.11 along with the

data points to inspect the quality of the fit.

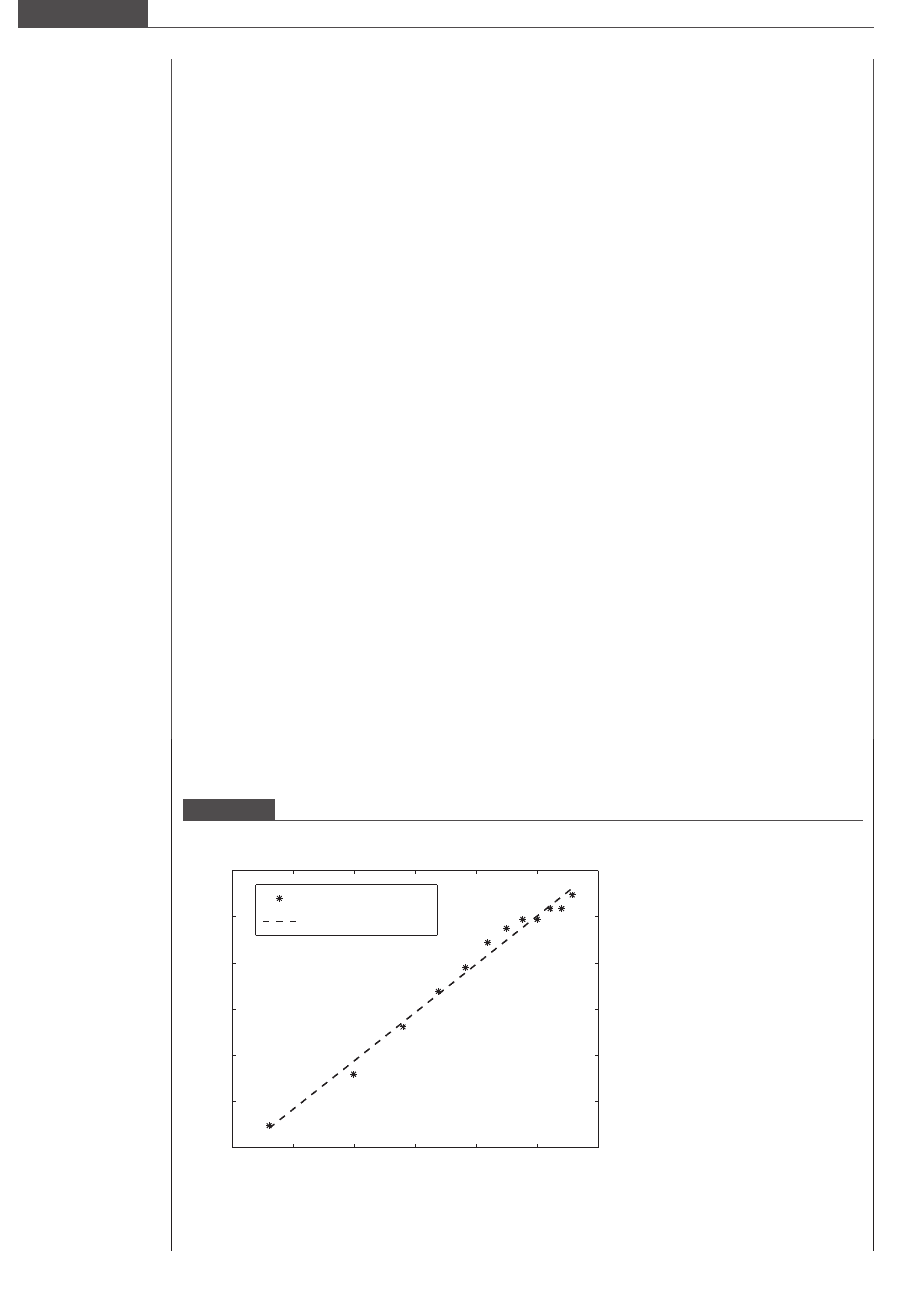
Figure 2.11

Transition from gliding to rotating motion. Quadratic curve fitted to data points (H, α

crit

0.45 0.5 0.55 0.6 0.65 0.7 0.75

Initial y-axis tilt, α

crit

(degrees)

Initial height H of platelet centroid (μm)

Data points, α

crit

Fitted quadratic curve

117

2.9 Curve fitting using linear least-squares method

It is a good idea to plot the residuals with respect to the independent variable and

visually inspect the residual plot to see if there is any observabl e trend in the

unexplained error. If the distribution of the residuals about zero appears to be

entirely random, then a trend in the residual error does not exist and the variations

in the data are approximately random (errors or ﬂuctuations are usually assumed to

be normally distributed; see Chapter 3). If a distinct trend is noticeable in the residual

values with respect to the independent variable, this suggests that the model is

incomplete and does not fully account for the observed trend in the data.

Note on the MATLAB backslash ( \) operator

The MATLAB backslash operator can solve overdetermined linear equations

Ac = y in which the number of equations m is greater than the number of variables

n. One simply needs to type

c = A\y

to obtain the least-squares ﬁt. MATLAB does not employ the normal equations

discussed in this chapter, but uses another method called QR factorization with

pivoting. QR factorization expresses the coefﬁcient matrix A as a product of two

matrices: an orthogonal matrix and an upper triangular matrix. Either method will,

under usual circumstances, produce the same result. The methods differ in terms of (i)

computational efﬁciency and (ii) stability in the face of minor ﬂuctuations in data

values (conditioning of the system). An analysis of the differences between various

methods employed for linear least-squares regression can be found in Demmel (1997).

2.10 Linear least-squares approximation of transformed equations

In the problems described in Boxes 2.2 and 2.3, the dependent variable does not have

a linear relationship with the undetermined coefﬁcients. In both cases, the nonlinear

equation is amenable to rearrangement such that the new form of the equation is a

straight line. These nonlinear equations are said to be transformed to a linear

equation. Such transformed equations have a linear relationship with respect to

their undetermined coefﬁcients, and can therefore be ﬁtted to data sets using the

linear least-squares method of regression. For example, many natural phenomena,

such as radioactive decay, population growth, chemical reaction rate, and forward/

backward chemical rate constants, exhibit an exponential dependence on some

factor or environmental condition (temperature, concentrations of chemicals etc.).

A nonlinear exponential dependency of m on t such as

m ¼ m

kt

is linearized by taking the natural logarithm of both sides:

ln m ¼ ln m

 kt:

The dependency of ln m on t is linear, and a straight line can be used to approximate

data that can be described by such a relationship. The linear least-squares line

estimates the two constants, m

and k, that characterize the process. If we make

the following substitutions:

y ¼ ln m; x ¼ t; β

¼k; β

¼ ln m

;

118

Systems of linear equations

then the model simpliﬁes to y ¼ β

x þ β

. The data points used to obtain a best-ﬁt

line that approximates the data are (x

, y

)or(t,lnm). The linear least-squares

technique calculates values of β

and β

that represent the best line ﬁt to data points

(ln m, t) and not (m, t). Therefore, it is important to keep in mind that a best-ﬁt

solution for the transformed data may not be as good a ﬁt for the original data. That

is why it is important to extract the constants m

and k from β

and β

and determine

the errors in the approximation with respect to the original data. Plotting the

original data and the ﬁtted curve to check the accuracy of the ﬁt is recommended.

Table 2.5 contains several additional examples of commonly encountered forms of

nonlinear equations and strategies to linearize them.

Table 2.5. Examples of nonlinear equations that can be linearized

Nonlinear

equation

Transformed equation

of form y ¼ a

x þ a

Transformed data

points

Transformed

coefﬁcients

m ¼ m

(power-law

model)

ln m ¼ k ln t þ ln m

y ¼ ln m; x ¼ ln t β

¼ k; β

¼ ln m

m ¼ m

log m ¼ kt þ log m

y ¼ log m; x ¼ t β

¼ k; β

¼ log m

m ¼ m

k þ t

y ¼

; x ¼ t β

; β

m ¼ m

k þ t

y ¼

; x ¼

; β

Box 2.2B Using hemoglobin as a blood substitute: hemoglobin–oxygen binding

We seek the best-fit values for the coefficients P

and n using the transformed linear equation

1  S

¼ n ln pO

ðÞn ln P

: (2:28)

Let

y ¼ ln

1  S

; x ¼ ln pO

ðÞ; β

¼ n; and β

¼n ln P

Equation (2.28) is rewritten as

y ¼ β

x þ β

Table 2.1 provides the data points (pO

, S), where pO

is given in units of mm Hg. At the command

line, we create the two variables x and y. Note that in MATLAB the log function calculates the natural

logarithm of a scalar or the individual terms in a vector.

pO2 = [10:10:120]’;

x = log(pO2);

S = [0.18; 0.40; 0.65; 0.80; 0.87; 0.92; 0.94; 0.95; 0.95;

0.96; 0.96; 0.97];

y = log(S./(1-S));

119

2.10 Linear least-squares approximation of transformed equations

The matrix A for this problem is

A = [x ones(size(x))];

The normal system is solved as shown below.

c=(A’*A)\A’*y

2.0906

−6.3877

Matrix c ¼



and the model coefficients are extracted from c as follows:

n = c(1)

2.0906

P50 = exp(-c(2)/n)

P50 =

21.2297

The x, y data are plotted in Figures 2.12 and 2.13 to check the fit. The code is presented below:

yhat = A*c;

plot(x,y,‘k*’,x,yhat,‘k–’,‘LineWidth’,2)

set(gca,‘FontSize’,16,‘LineWidth’,2)

xlabel(‘log({\itp}O_2)’)

ylabel(‘log({\itS}/(1-{\itS})’)

legend(‘transformed data’,‘ﬁtted line’)

S_hat = (pO2.^n)./(P50^n+(pO2.^n));

plot(pO2, S, ‘k*’,pO2,S_hat,‘k–’,‘LineWidth’,2)

set(gca,‘FontSize’,16,‘LineWidth’,2)

xlabel(‘{\itp}O_2 in mmHg’)

ylabel(‘{\itS}’)

legend(‘original data’,‘ﬁtted line’)

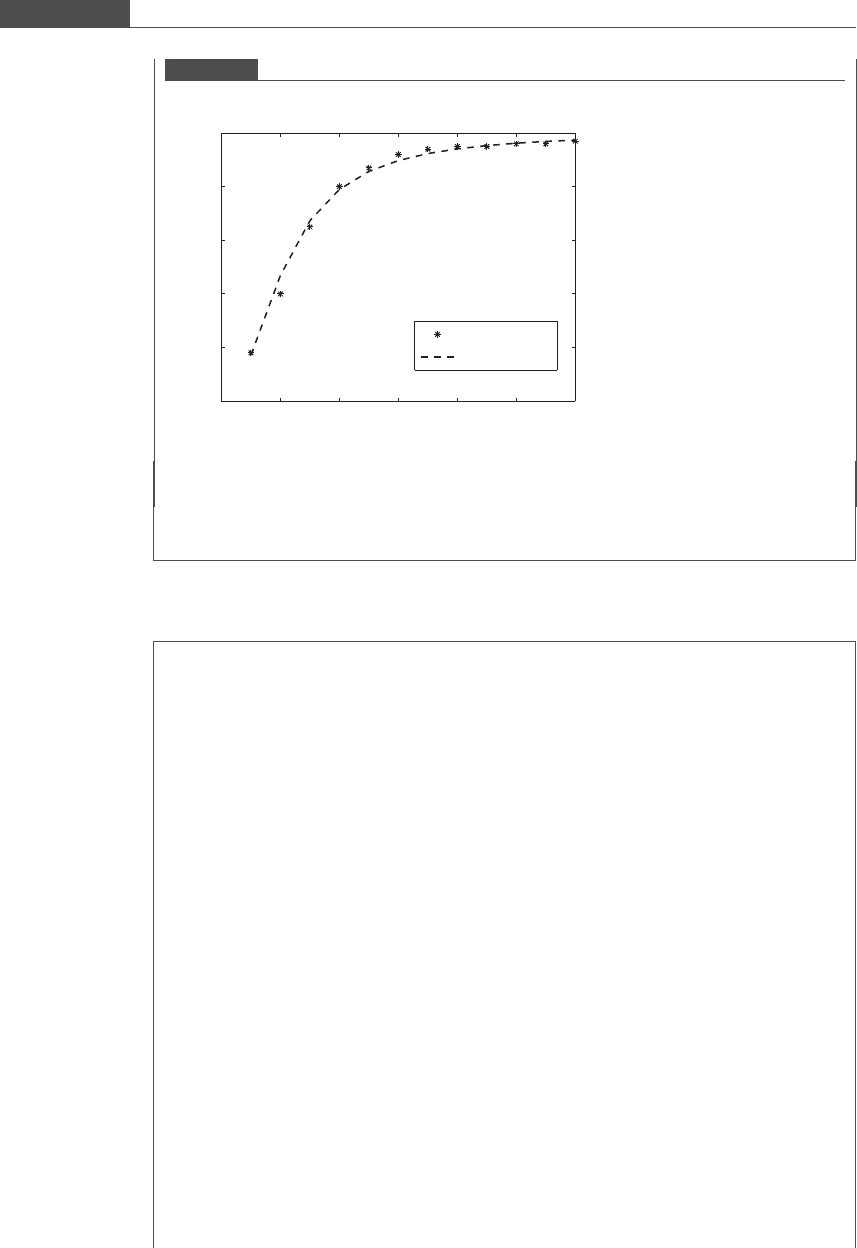
Figure 2.12

Transformed oxygen dissociation curve.

2 2.5 3 3.5 4 4.5 5

−2

−1

log(pO

)

log(S/(1−S)

Transformed data

Fitted line

120

Systems of linear equations

The typical P

value for human hemoglobin in blood is 26 mm Hg (Imai et al., 2001). The P

value

for tetrameric bovine hemoglobin is lower than that for the normal case, indicating higher affinity of

bovine hemoglobin for oxygen. Such values are typically found in diseased (hemoglobinopathic)

conditions and may not be suitable for in vivo use as a blood substitute (Imai et al., 2001).

Figure 2.13

Original oxygen dissociation curve with model prediction.

0 20 40 60 80 100 120

0.2

0.4

0.6

0.8

(mmHg)

Original data

Fitted line

Box 2.3B Time course of drug concentration in the body

The transformed linear equation that we use to determine the “best-fit” values for the coefficients C

and

k is as follows:

ln CtðÞ¼ln C

 kt: (2:30)

Let y ¼ ln C, x ¼ t, β

¼k, and β

¼ ln C

. Equation (2.30) is rewritten as

y ¼ β

x þ β

Table 2.2 lists the data points (t,lnC

) and (t,lnC

). In a script file, we create three variables x, y

, and y

as shown below. Equation (2.30) is not defined for C

or C

= 0 and therefore we do not include the zero

concentration data points.

t = [1 2 3 8 16 24 48]’;

Cv = [18.912 13.702 7.406 2.351 0.292]’;

Ca = [0.240 0.187 0.127]’;

x = t; yv = log(Cv); ya = log(Ca);

For the linear equation y ¼ β

x þ β

, the matrix A is given by

A = [x ones(size(x))];

Av = A(1:length(Cv),:);

Aa = A(1:length(Ca),:);

The normal system is solved as follows:

cv = (Av’*Av)\(Av’*yv);

ca = (Aa’*Aa)\(Aa’*ya);

121

2.10 Linear least-squares approximation of transformed equations

Since c ¼



, the model coefficients are extracted as shown below:

kv = − cv(1)

C0v = exp(cv(2))

ka = − ca(1)

C0a=exp(ca(2))

The MATLAB output of the script is

kv =

0.2713

C0v =

21.4204

ka =

0.3182

C0a =

0.3376

To determine whether the drug clearance rates k are similar or different for the vitreous and aqueous

humor, we would need to carry out a hypothesis test. Hypothesis tests are statistical tests that determine

with some confidence level (probability) if the apparent differences between two means (or parameters)

obtained from two distinct samples are due to chance or whether they actually signify a legitimate

difference in the populations from which the samples have been derived (see Chapter 4). The transformed

data points and the best-fit models are plotted in Figure 2.14 and the relevant code of the script is

presented below.

% Plotting least-squares ﬁt for drug elimination from the Vitreous

subplot(1,2,1)

plot(x(1:length(Cv)),yv,‘k*’,x(1:length(Cv)),Av*cv,‘k–’, ...

‘LineWidth’,2)

xlabel(‘{\it t} in hours’)

ylabel(‘log({\itC_v})’)

legend(‘transformed data’,‘best-ﬁt model’)

% Plotting least-squares ﬁt for drug elimination from the Aqueous

subplot(1,2,2)

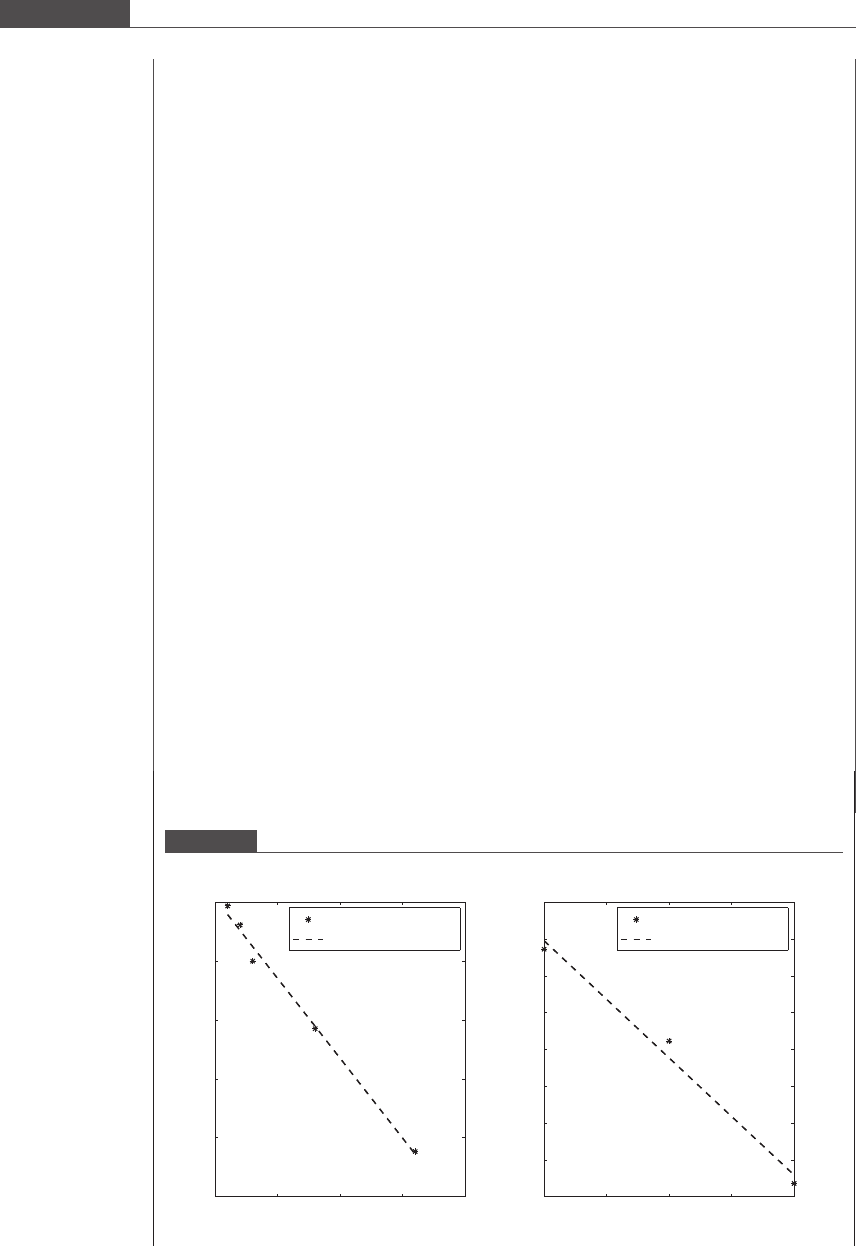
Figure 2.14

Drug elimination profile using transformed coordinates.

0 5 10 15 20

−2

−1

t (hours)

log(C

)

Transformed data

Best−fit model

1 1.5 2 2.5 3

−2.1

−2

−1.9

−1.8

−1.7

−1.6

−1.5

−1.4

−1.3

t (hours)

log(C

)

Transformed data

Best−fit model

122

Systems of linear equations

Exponential, power-law, logarithmic, and rational functions are all subject to

certain speciﬁc limitations in the data, such as:

a reciprocal function in 1/t cannot include the point t =0;

logarithmic functions in x are valid strictly for x >0;

an exponential function in y does not allow a sign change in y.

Polynomial functions are, on the other hand, more ﬂexible and do not have such

limitations. These are important limitations to keep in mind when selecting a ﬁtting

function.

2.11 Multivariable linear least-squares regression

At times, we may model the simultaneous dependency of one variable on two or

more independent variables. Equation (2.31) is an example of the linear dependency

of y on more than one independent variable. Of course, the dependency need not be

linear for any physical, chemical, or biological process, and linear least-squares

regression can still be applicable in many cases. For example, the biochemical

reaction below states that enzyme E must combine with substrates A and B in

order to catalyze the irreversible reaction to form product P:

E þ aA þ bB ! E þ P:

An example of an enzyme reaction that acts on two substrates is L-asparagine

hydrolysis, which is catalyzed by the enzyme L-asparaginase via the deamination

reaction

L-asparagine þ H

! L-aspartate þ NH

Normal cells are capable of synthesizing asparagine, whereas certain leukemia

cells are unable to do so, although they require L-asparagine for their growth and

survival. L-asparaginase has been found to act as an anti-cancer agent and acts to

remove all asparagine externally available to cells. As the internal supply of

asparagine becomes depleted, the cancer cells die (Livingston and Krakoff, 1970).

The reaction rate r = kC

, where k is the reaction rate constant, C

is the

concentration of enzyme in solution, C

is the concentration of substrate A in

solution, and C

is the concentration of substrate B in solution. Rate r is a function

of three independent co ncentration variables, and k, a, and b are the coefﬁcien ts that

are calculated from experiments that measure a range of reaction rates as a function

of concentration values of each reacting substance. How do we approach this

regression problem?

An equation of the form m ¼ kt

is called a multivariable power-law equation.

This equation can be linearized by taking the logarithm of both sides to obtain

ln m ¼ ln k þ p ln t

þ q ln t

þ r ln t

: (2:48)

plot(x(1:length(Ca)),ya,‘k*’,x(1:length(Ca)),Aa*ca,‘k–’, ...

‘LineWidth’,2)

xlabel(‘{\it t} in hours’)

ylabel(‘log({\itC_a})’)

legend(‘transformed data’, ‘best-ﬁt model’)

123

2.11 Multivariable linear least-squares regression

If we substitute y ¼ m; x

¼ ln t

; x

¼ ln t

; x

¼ ln t

, and β

¼ ln k; β

¼ p;

¼ q; β

¼ r, Equation (2.48) becomes

y ¼ β

þ β

: (2:49)

Equation (2.49) has four unknowns: β

, β

. The normal equations A

Ac ¼

y apply, where

A ¼

1 x

1;1

2;1

3;1

1 x

1;2

2;2

3;2

1 x

1;m

2;m

3;m

; c ¼

; and y ¼

The second subscript in the individual terms of A indicates the 1 ≤ i ≤ m data

points.

Equation (2.49) presents the simple dependence of y on the independent variables.

Remember that, while the model must be linear in the model parameters β, the

relationships between the dependent and independent variables need not be linear.

The normal system can be applied for linear regression if the model is, for example,

y ¼ a

þ a

ln x

þ a

sin x

2.12 The MATLAB function polyﬁt

MATLAB provides a built-in function called polyﬁt that uses the linear least-squares

method to ﬁt a polynomial in x of degree n to a set of data y. The syntax for this function is

p = polyﬁt(x, y, n)

where x is the independent variable vector, y is the dependent variable vector, n is the

degree of the polynomial, and p is a vector containing the n+1 coefﬁcients of the

polynomial in x. The coefﬁcients of the polynomial in p are arranged in descending

order of the powers of x. The MATLAB polyﬁt function uses the QR facto rization

method to solve overdetermined systems using the least-squares method.

Box 2.4C Platelet Flow Rheology

We wish to fit the function α

crit

¼ β

þ β

H þ β

, where α

crit

is the critical angle of tilt of the platelet at

which the transition in flow behavior occurs.

The vectors H and α contain the data to be fitted by a second-order polynomial:

H = [0.5 0.55 0.6 0.65 0.7];

alpha = [10.5 10 8.5 7.0 4.5];

c = polyﬁt(H, alpha, 2)

-114.2857 107.1429 -14.4714

The least-squares fitted polynomial is

crit

¼114:2857H

þ 107:1429H  14:4714:

124

Systems of linear equations

2.13 End of Chapter 2: key points to consider

Concepts from linear algebra and MATLAB programming

(1) A one-dimensional array is called a vector and a two-dimensional array is called a

matrix.A1× 1 array is a scalar.

(2) The dot product of two vectors is deﬁned as u  v ¼

i¼n

i¼1

, where both vectors have

the same number of elements n. To obtain the dot product of two vectors, a column

vector on the right must be pre-multiplied by a row vector on the left. The dot

product is an example of matrix–matrix multiplication in which a 1 × n matrix is

multiplied with an n × 1 matrix.

(3) Matrix–matrix multiplication of A with B is deﬁned if A is an m × n matrix and B is an

n × p matrix, i.e. their inner dimensions must agree. The resulting matrix C = AB has

the dimensions m × p. Every element c

of C is equal to the dot product of the ith row

of A and the jth column of B.

(4) The norm of a vector is a real number that speciﬁes the length of the vector. A p-norm

is a general metho d used to calculate the vector length and is deﬁned, for vector v,

as kvk

i¼1



1=p

. The p = 2 norm (Euclid ean norm) is deﬁned as

kvk¼

ﬃﬃﬃﬃﬃﬃﬃﬃ

v  v

i¼n

i¼1



1=2

(5) The norm of a matrix A is a measure of the maximum degree to which A can stretch a

unit vector x. Mathematically, we write kAk¼max

kxk¼1

kAxk.

(6) A linear combination of vectors is the sum of one or more vectors of equal dimension,

each multiplied by a scalar, and results in another vector of the same dimension.

If V ¼ðv

; v

; ...; v

Þ is a set of vectors, and if u ¼ k

þ k

þþk

, where k

for 1 ≤ i ≤ n are scalars, then u is said to be a linear combination of the given set of

vectors V.

(7) If V ¼ðv

; v

; ...; v

Þ is a set of vectors, and the vector equation k

þ k

þþ

¼ 0 holds true only when all k

= 0 for 1 ≤ i ≤ n, then the vectors are said to be

linearly indepen dent . If it holds true for non-zero values of the scalars, i.e. there exists

multiple solutions to the vector equation, then the vectors in set V are linearly

dependent.

(8) A vector space S that contains a set of vectors V must also contain all vectors that

result from vector addition and scalar multiplication operations on the set V, i.e. all

possible linear combinations of the vector s in V. The physical three-dimensional

space that we live in is a vector space. If the vectors in the set V are linearly

independent, and all possible linear combinations of these vectors fully describe

the vector space S, then these vectors are called basis vectors for the space S.

The number of basis vectors that are required to describe the vector space S fully

is called the dimension of the vector space.

(9) The vector space spanned by the columns of a matrix is called the column space.

(10) The determinant of a matrix is deﬁned only for square matrices and is a scalar

quantity. The determinant of an n × n matrix is the sum of all possible products of

n elements of matrix A, such that no two elements of the same row or column are

multiplied together. A matrix that has a non-zero determinant is called non-singular,

whereas a matrix whose determinant is equal to zero is singular.

(11) The rank of a matrix A is the dimension of the largest submatrix within A that has

a non-zero determinant. Equivalently, the rank of a matrix is equal to the dimension of

the column space of the matrix A, i.e. the number of linearly independent columns in A.

125

2.13 Key points

(12) The inverse of a matrix A is denoted as A

1

and is only deﬁned for non-singular

square matrices. When a matrix is multiplied by its inverse, the identity matrix I is

obtained: AA

1

¼ A

1

A ¼ I .

Solution techniques for systems of linear equations

(1) A system of linear equations can be compactly represented by the matrix equation

Ax = b, where A is the coefﬁcient matrix, b is the vector of constants, and x is the

vector containing the unknowns.

(2) The rank of the coefﬁcient matrix A and the augmented matrix [Ab] tells us whether

(a) a unique solution exists,

(b) inﬁnitely many solutions exist, or

for a system of linear equations Ax = b.

(3) Gaussian elimin ation is a direct method that is used to solve consistent systems

of linear equations Ax = b for which the determinant of the coefﬁcient matrix

6¼ 0.

(a) Gaussian elimination reduces the augmented matrix [Ab]toupper triangular form.

(b) The pivot row is used to zero the elements in rows below it. The column in which

the elements are being zeroed is called the pivot column.Thepivot element is

locatedinthepivotrowandpivotcolumnandisusedtozerotheelements

beneath it.

(4) Backward substitution works backwards from the last equation of the linear system,

speciﬁed by the upper triangular form of the augmented matrix [Ab] that results

from Gaussian elimination, to the ﬁrst, to obtain the solution x. For a system of n

equations in n unknowns, x

is obtained ﬁrst using the last (bottom-most) equation

speciﬁed by [Ab]. The knowledge of x

is used to obtain x

n1

using the second-last

equation from [Ab]. This procedure continues until x

is obtained.

(5) Gaussian elimination fails if any of the elements along the main diagonal of the

augmented matrix is either exactly zero or close to zero. Partial pivoting is used to

remove zeros or small numbers from the diagonal. Before any zeroing of elements is

performed, the pivot element in the pivot row is compared with all other elements in

the pivot column. Row swapping is carried out to place at the pivot row position, the

row containing the element with the largest absolute magnitude.

(6) LU factorization is a direct method to solve systems of linear equations and is most

useful when the same coefﬁcient matrix A is shared by several systems of equations.

In this method, A is factorized into two matrices: a lower triangular matrix L and an

upper triangular matrix U, i.e. A = LU. Note that U is the same as the upper

triangular matrix that results from Gaussian elimination, and L contains the multi-

pliers that are used to zero the below-diagonal entries in the augmented matrix. In

this process , we decouple the transformations carried out on A from that on b. Two

sequential steps are required to extract the solution:

(a) forward substitution to solve Ly = b;

(b) backward substitution to solve Ux = y.

(7) Pivoting or exchanging of rows is recommended when performing LU factorization

in order to limit round-off errors generated during elimination steps. A permutation

matrix P must be used to track row swaps so that b can be transformed accordingly

prior to forward substitution. Mathematically, LU = PA and LUx = Pb.

(8) A problem is said to be ill-conditioned if the solution is hypersensitive to small

changes in the coefﬁcients and constants of the linear equations. On the other

126

Systems of linear equations