Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие
Подождите немного. Документ загружается.

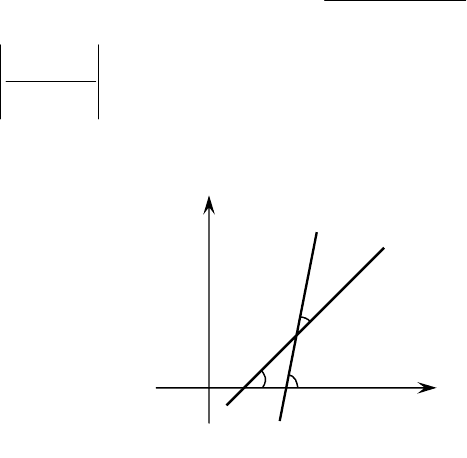
Угол между прямыми
Даны уравнения прямых
:
1
l
11
bxky
+
⋅
=
, :
2
l
22
bxky +⋅
=
.
Угол между прямыми
α
=
∧
21
, ll ,
12
ϕ
ϕ
α
−
=
.
()
21
12
12
1
ϕϕ
ϕ
ϕ
ϕϕα
tgtg
tgtg
tgtg
+
−
=−= ,
т.е.
21
12
21
1
,
kk
kk
tg
+
−
=
∧
ll
.
Наличие модуля в формуле позволяет находить сразу острый угол между
прямыми.
y
2
l
1
l
α
1
ϕ
2
ϕ
0
x
Рис. 3
С л е д с т в и я
1.
Условие параллельности прямых.
Если,
21
|| ll
то
0
21
==
∧
ll
α
,
21
0 kktg
=
⇔
=
α
.
2121
|| kk
=
⇔
ll .
2. Условие перпендикулярности прямых
1
2121
−
=
⋅
⇔
⊥
kkll .
Общее уравнение прямой
Всякое уравнение первой степени вида
0
=
+
+
C
By
Ax
,
(где
C
B
A
,,
– постоянные, причем
0
22
≠
+
B
A
), определяет на плоскости
прямую. Это уравнение называется
общим уравнением прямой. Вектор
{}
BA, называется нормалью прямой.
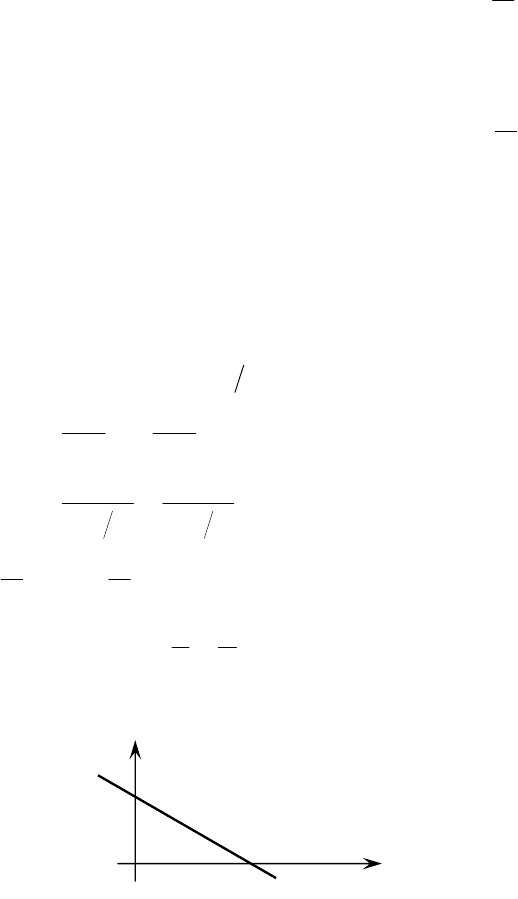
Частные случаи
1. 0=
C
, 0≠
A
, 0
≠
B .
Прямая, определяемая уравнение
0
=
+
By
A
x
проходит через начало коорди-
нат.
2.
0=
A
,
0≠B
,
0
≠
C
.
Прямая определяемая уравнением
0
=
+
C
By
или
B
C
by
−== , параллельна
оси
Ох.
3. 0=B , 0≠
A
, 0
≠
C
.
Прямая, определяемая уравнением 0
=
+
C
A
x или
A
C
ax
−==
, параллельна
оси
Оу.
4. 0=
C
, 0=
A
, 0
≠
B .
Прямая, определяемая уравнением
0
=
By
или
0
=
y
− это ось Ох.
5. 0=
C
, 0=B , 0
≠
A
.
Прямая вида
0=
A
x
или
0=
x
− это ось Оу.
6. Если 0≠
A
, 0≠B , 0≠
C
, то уравнение можно преобразовать:
C
By
Ax
−
=
+
(
)
C
−
:;
1=
−
+
−
y
C
B
x
C
A
;
1=
−
+
− BC
y
AC
x
.
Обозначим
a
A
C
=−
;
b
B
C
=−
, получим
уравнение прямой в отрезках:
1=+
b
y
a
x
.
Числа
ba,
– это отрезки, отсекаемые прямой на координатных осях.
Рис. 4
Рассмотрим две прямые 0
111
=
+
+
CyBxA и 0
222
=+
+
CyBxA .
y
a
b
0
x
1. Если
2
1
2
1
B
B
A
A
=
, то прямые параллельны.
2. Если
2
1
2
1
2
1
C
C
B
B
A
A
== , то прямые совпадают.
3. Если
2
1
2
1
B
B
A
A
≠
, то прямые пересекаются.
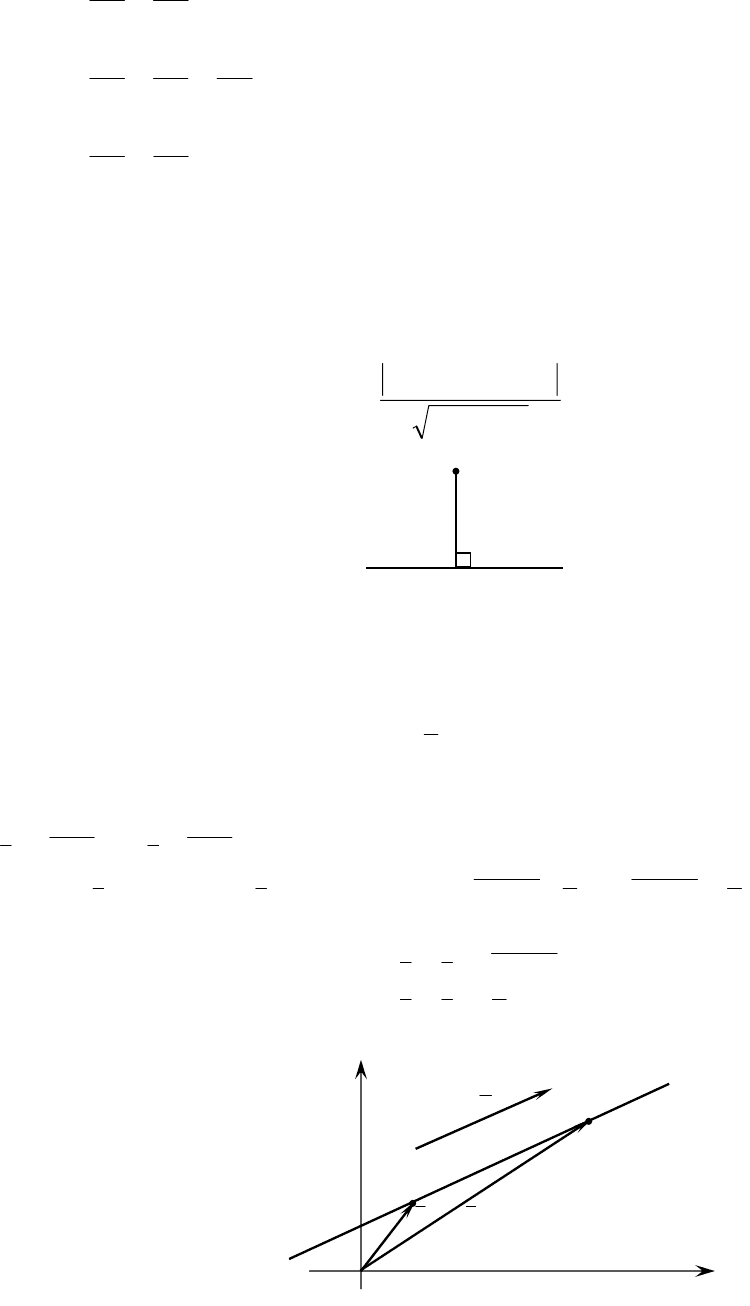
Расстояние от точки до прямой
Рассмотрим прямую
0
=
+
+
C
By
A
x
и точку
(
)
000
, yxM . Расстояние от
точки до прямой находит по формуле
22
00
BA
CByAx
d
+
++
=
.
Рис.5
Векторное уравнение прямой
Рассмотрим прямую и вектор
{
}
0,
≠
=
ma l
параллельный прямой. Вся-
кий такой вектор называется
направляющим.
Пусть на прямой даны две точки
(
)
000
, yxM и
(
)
yxM , . Тогда векторы
0
0
OMr = и OM
r
= называются радиус-векторами точек
0
M ,
M
. Их коор-
динаты
{}
000
, yxr =
;
{}
yxr ,=
. Так как
aMM ||
0
, то
taMM ⋅=
0
, где
t
– не-
которое число (параметр).
MMrr
00
+=
;
tarr
+
=
0
.
y
a
(
)
yxM ,
(
)
000
, yxM
0
r
r
0
x
(
)
000
, yxM
d
0
=
+
+
C
By
A
x
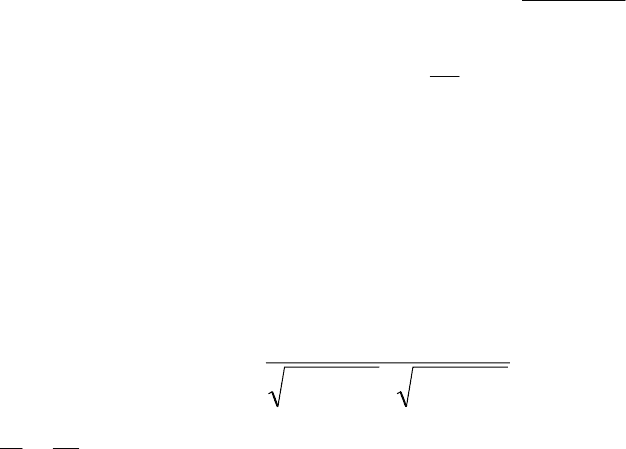
Рис. 6
Это и есть векторное уравнение прямой.
Параметрическое уравнение прямой
Запишем векторное уравнение прямой в координатах
{}
{
}
{
}
tmyxyx
⋅
+
=
,,,
00
l
или
⎩
⎨
⎧
+=
+=
.
;
0
0
tmyy
txx l
Это параметрическое уравнение прямой. Здесь
(
)
00
, yx – координаты точки
на прямой,
{}
m,l
– координаты направляющего вектора.
Рассмотрим теперь взаимное расположение прямых,
заданных различными уравнениями.
1. Пусть даны прямые
:
1
l
11
bxky
+
⋅
=
,
:
2
l
22
bxky +
⋅
=
. Тогда угол
между этими прямыми определяют по формуле
21
12
1 kk
kk
tg
⋅+
−
=
α
.
Условие перпендикулярности:
2
121
1
k
kll −=⇔⊥
;
условие параллельности:
2121
|| kkll
=
⇔
.
2. Пусть две прямые заданы общими уравнениями
:
1
l
0
111
=
+
+
CyBxA
,
:
2
l 0
111
=
+
+
CyBxA .
Тогда угол
α
между этими прямыми равен углу между их нормалями
{}
111
, BAn = и
{}
222
, BAn
=
т.е.
2
2
2
2
2
1
2
1
2121
cos
BABA
BBAA
+⋅+
⋅
+
⋅
=
α
Условие перпендикулярности:
21212121
BBAAnnll ⋅+⋅⇔⊥⇔⊥
.
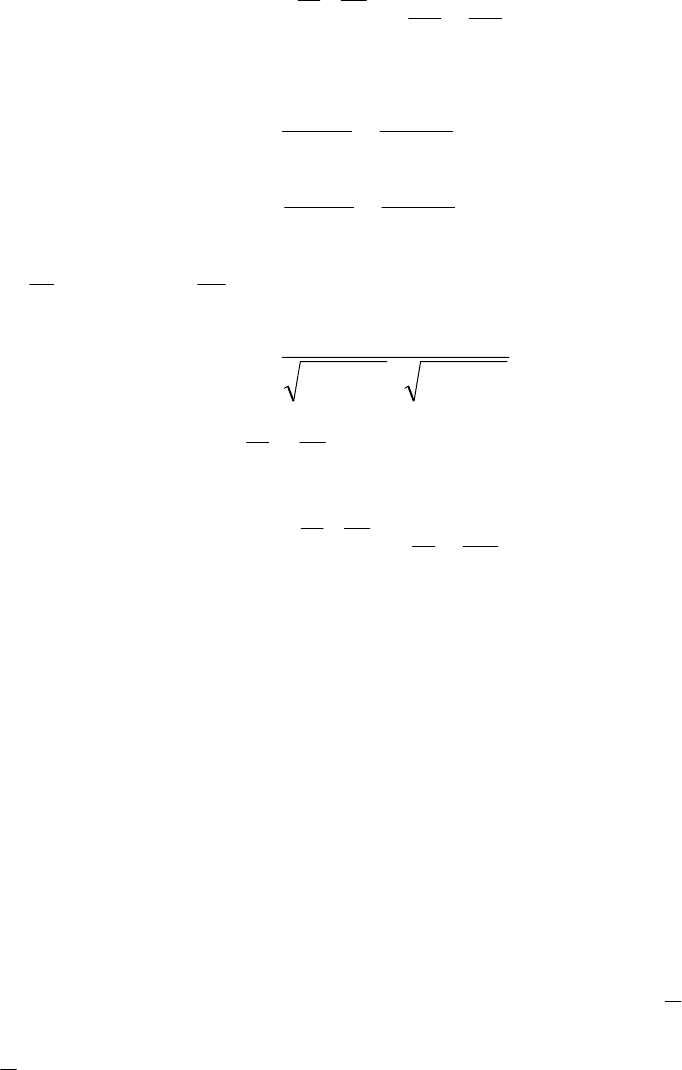
Условие параллельности:
2
1
2
1
2121
||||
B
B
A
A
nnll =⇔⇔
.
3. Пусть прямые
1
l
и
2
l
заданы каноническими уравнениями
:
1
l
1
0
1
0
m
yy
l
xx
−
=
−
,
:
2
l
2
0
2
0
m
yy
l
xx
−
=
−
.
Тогда угол
α
между прямыми совпадает с углом
α
между направляющими
векторами
{}
111
, mla =
и
{
}
222
, mla =
2
2
2
2
2
1
2
1
2121
cos
mlml
mmll
+⋅+
⋅
+
⋅
=
α
Условие перпендикулярности:
0
21212121
=⋅+⋅⇔⊥⇔⊥ mmllaall
.
Условие параллельности:
2
1
2
1
2121
||||
m
m
l
l
aall =⇔⇔
.
Примеры решения задач
1. Написать уравнения прямых, проходящих через точку
()
1,2
0
−M парал-
лельно, перпендикулярно и под углом
o
45 к прямой
42
−
=
x
y
.
Решение.
Для решения задачи воспользуемся уравнением прямой, проходящей через
заданную точку. Имеем уравнение
(
)
21
−
⋅
=
+
xky
.
Определим
k
прямой. Если прямая параллельна данной прямой
42
−=
x
y
, то
2
=
k
и
0520142421
=
−
−
⇒
=
−
−
−⇒−=+ y
x
y
x
x
y
– это уравнение
прямой, параллельной данной.
Если искомая прямая перпендикулярна данной, то
2
1
−=k и тогда
()
0202222
2
1
1 =+⇒=−−+−⇒−−=+ yxyxxy
– это уравнение прямой,
перпендикулярной данной.
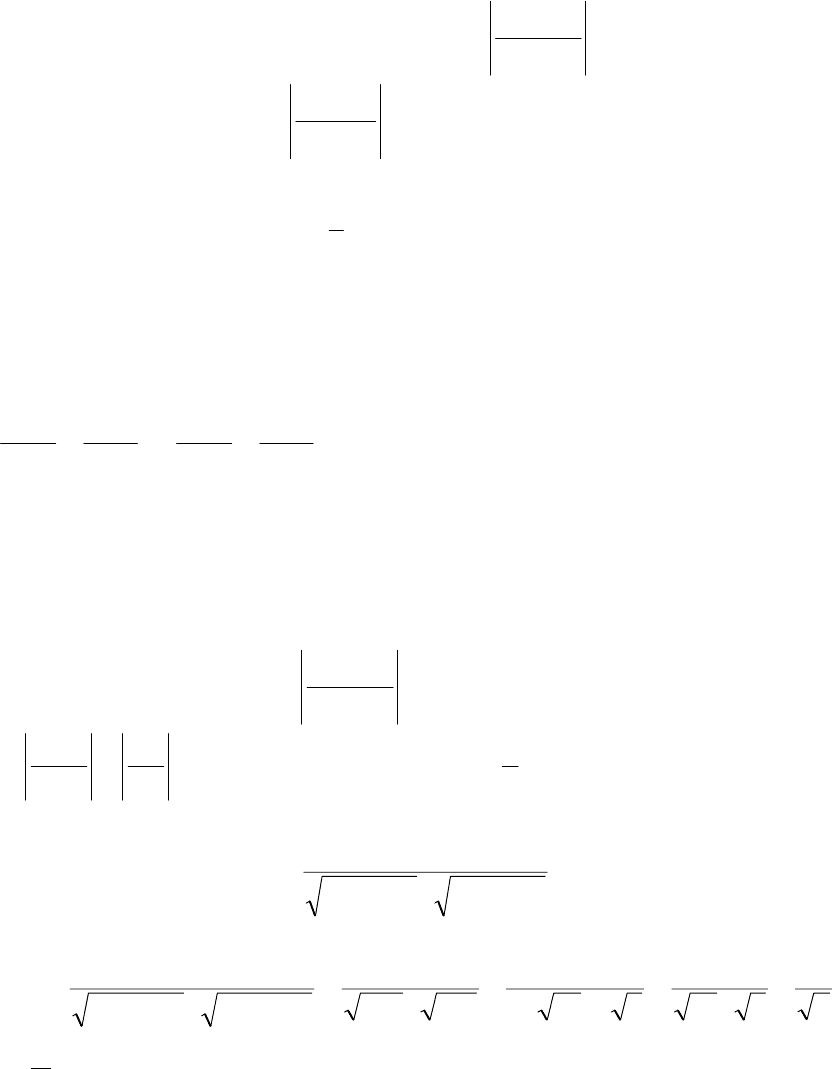
Определим далее угловой коэффициент прямой, проходящей под углом
o
45 к
данной прямой
42 −=
x
y
, по формуле
21
12
1 kk
kk
tg
+
−
=α
. Подставляя в эту фор-
мулу
o
45=
α
получим:
1
1
21
2
1
k
k
+
−
=
(так как угловой коэффициент данной
прямой 1=k ).
Имеем
()
3
1
221
111
=⇒−±=+ kkk или 3
1
−
=
k . И тогда
053 =−+
x
y
и
053 =+−
x
y
– уравнения прямых, проходящих под углом
o
45 к данной.
2. Найти уравнение прямой, проходящей через точки
(
)
1,5
1
−
A и
()
5,2
2
A .
Решение.
Воспользуемся уравнением прямой, проходящей через две точки
()()
⇒=++−⋅⇒+−=−⇒
+
=
−
−
⇒
+
+
=
−
−
01102152
6
1
3
5
15
1
52
5
yxyx
yxyx
092 =−+⋅⇒ y
x
.
3. Найти угол между прямыми:
а)
x
y ⋅= 3
и
52 +⋅−=
x
y
; б)
017618
=
−
⋅
+
⋅
y
x
и
0105 =⋅+
⋅
y
x
.
Решение.
а) Для вычисления угла между прямыми с угловым коэффициентом восполь-
зуемся формулой
21
12
1 kk
kk
tg
+
−
=α
. Но
3
1
=
k
,
2
2
−=k
, поэтому
1
5
5
61
23
=
−
=
−
+
=αtg
. Отсюда
()
o
45
4
1
1arctg ==+=
πα
.
б) В случае задания прямых общими уравнениями угол между прямыми мож-
но искать по формуле
2
2
2
2
2
1
2
1
2121
cos
BABA
BBAA
+⋅+
⋅
+
⋅
=
α
.
Имеем
2
1
510
5
55106
150
125360
150
105618
106518
cos
2222
=
⋅
=
⋅⋅
=
⋅
=
+⋅+
⋅
+
⋅
=
α
.
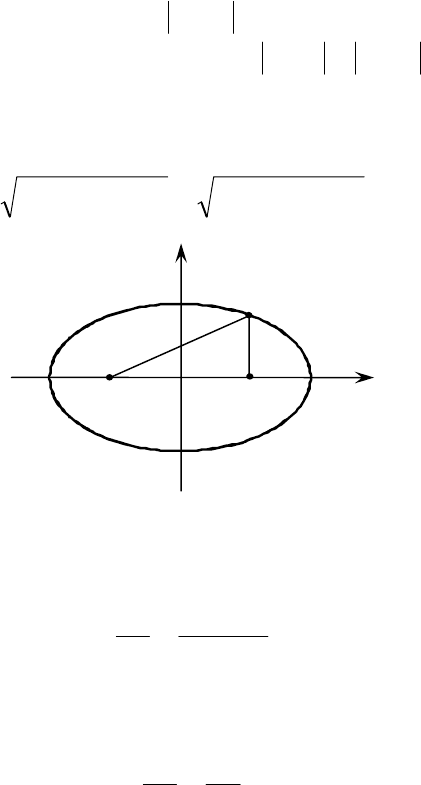
4
π
α
= .
§3. Кривые второго порядка
К кривым второго порядка считаются эллипс, гипербола, парабола.
Эллипс
Эллипсом называется геометрическое место точек плоскости, для каж-
дой из которых сумма расстояний до двух фиксированных точек называемых
фокусами, есть величина постоянная
а2 .
Пусть
21
, FF – два фокуса.
cFF 2
21
=
– расстояние между фокусами.
Если
M
– произвольная точка эллипса, то
caMFMF 22
21
>
=
+
.
Введем систему координат так, чтобы фокусы находились на оси
Ох
симметрично относительно начала координат.
Составим уравнение эллипса
() ()
aycxycx 2
2
2
2
2
=+−+++
.
Рис. 7
После преобразований приходим к уравнению
1
22
2
2
2
=
−
+
ca
y
a
x
.
Обозначим
222
bca =−
, получим каноническое уравнение эллипса с
центром в начале координат
1
2
2
2
2
=+
b
y
a
x
,
(
cba ,,
− параметры эллипса;
ba,
− полуоси).
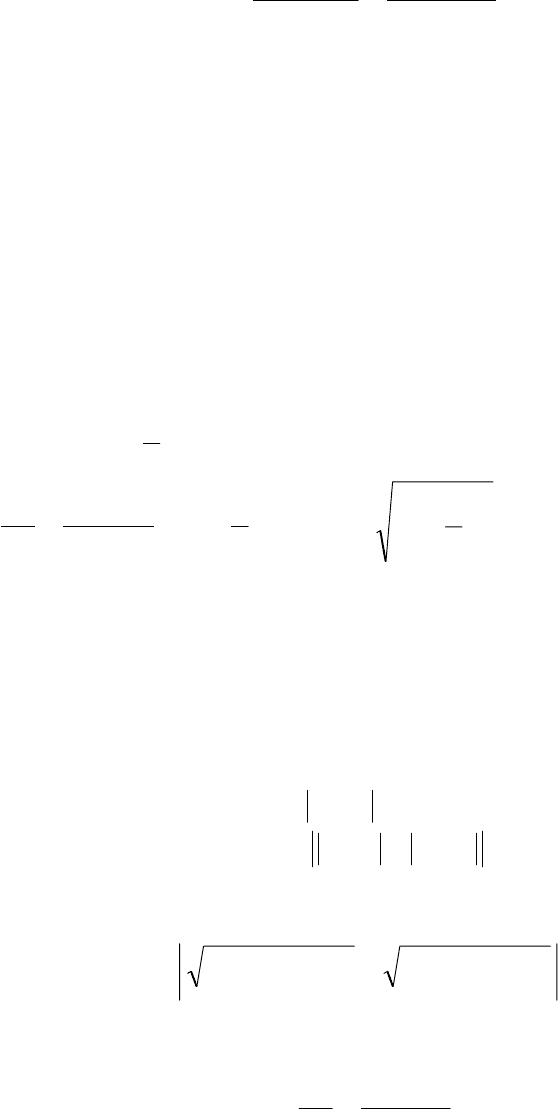
Если центр эллипса находится в точке
(
)
00
, yx
, то уравнение эллипса
имеет вид
x
y
0
b
a
1
F
2
F
()
0,c−
(
)
0,c
−
b
−
a
()
(
)
1
2
2
0
2
2
0
=
−
+
−
b
yy
a
xx
.
Если полуоси эллипса совпадают Rba
=
=
, то эллипс становится ок-
ружностью с уравнением
()
(
)
2
2
0
2
0
Ryyxx =−+− ,
()
00
, yx
− центр окружности,
R
− радиус.
Параметрическое уравнение эллипса
⎩
⎨
⎧
=
=
.sin
;cos
tby
tax
Параметрическое уравнение окружности
⎩
⎨
⎧
=
=
.sin
;cos
tRy
tRx
Число
a
с
=
ε
называется эксцентриситетом эллипса 1>
ε
. Так как
2
2
22
2
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
−=
−
==
a
b
a
ba
a
c
ε
, то
2
1
⎟
⎠
⎞
⎜
⎝
⎛
−=
a
b
ε
, 10
.
<
<
эл
ε
. Чем больше экс-
центриситет, тем сильнее сжат эллипс по вертикали.
Гипербола
Гиперболой называется геометрическое место точек плоскости, для
каждой из которых разность расстояний до двух фиксированных точек – фо-
кусов есть величина постоянная
a2
.
Пусть
21
, FF
– фокусы.
cFF 2
21
=
– расстояние между фокусами. Ес-
ли
M
− точка на гиперболе, то
aMFMF 2
21
=−
,
(
)
ac >
.
Если координаты фокусов
(
)
0;
1
cF
−
;
(
)
0;
2
cF ,
(
)
yxM , , то уравнение
гиперболы примет вид
() ()
aycxycx 2
2
2
2
2
=+−−++
После преобразований приходим к каноническому уравнению гипербо-
лы с центром в точки 0.
1
22
2
2
2
=
−
−
ac
y
a
x
.
Обозначим
222
bac =− , получим уравнение
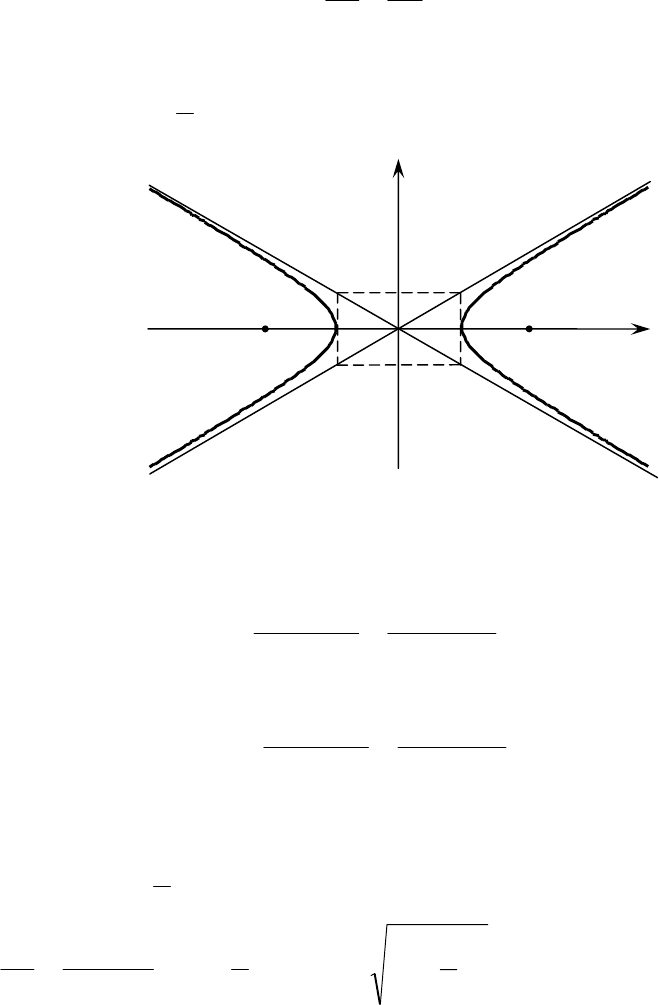
1
2
2
2
2
=−
b
y
a
x
,
ba,
− полуоси гиперболы.
Прямые
x
a
b
y ±=
являются асимптотами гиперболы.
Рис. 8
Если центр гиперболы смещен в точку
(
)
00
, yx , уравнение принимает
вид
()
(
)
1
2
2
0
2
2
0
=
−
−
−
b
yy
a
xx
.
Уравнение вида
()
(
)
1
2
2
0
2
2
0
=
−
+
−
−
b
yy
a
xx
.
Определяет гиперболу, ветви которой направлены вверх и вниз
∩
∪
.
Число
a
с
=
ε
называется эксцентриситетом гиперболы так как
2
2
22
2
2
2
1
⎟
⎠
⎞
⎜
⎝
⎛
+=
+
==
a
b
a
ba
a
c
ε
, то
2
1
⎟
⎠
⎞
⎜
⎝
⎛
+=
a
b
ε
, 1
гип.
>
ε
. Чем меньше эксцен-
триситет, тем сильнее сжат эллипс по вертикали.
Парабола
x
y
c
−
c
−
b
a
b
2
F
1
F
0
−a
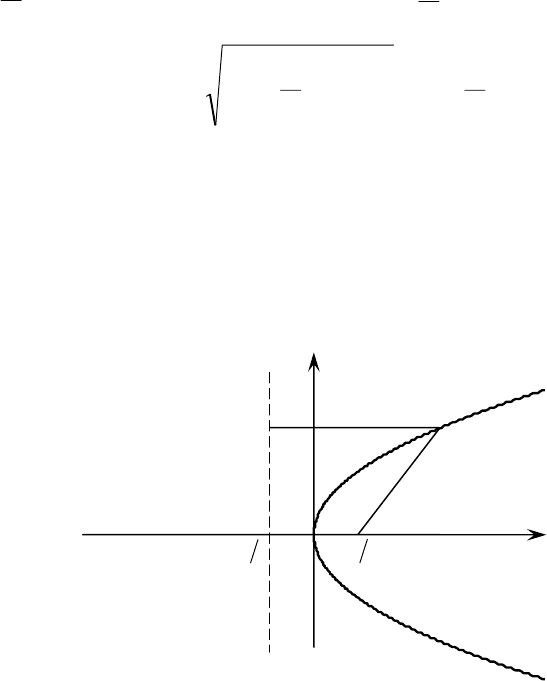
Параболой называется геометрическое место точек плоскости, для ка-
ждой из которых расстояние до точки фокуса равно расстоянию до некоторой
фиксированной прямой – директрисы (директриса не проходит через фокус).
Расстояние от фокуса
F
до директрисы равно
p
. Пусть
F
имеет коор-
динаты
⎟
⎠
⎞
⎜
⎝
⎛
0;
2
p
; уравнение директрисы
2
p
x −=
. Тогда уравнение параболы
22
2
2
p
xy
p
x +=+
⎟
⎠
⎞
⎜
⎝
⎛
− .
Его можно привести к каноническому уравнению
pxy 2
2
=
.
Если
0>
p
, ветви параболы направлены вправо.
Если
0<
p
, ветви направлены влево.
Уравнение
pyx 2
2
=
определяет параболу, у которой ветви направлены
вверх или вниз.
Рис. 9
Если вершина параболы – точка
(
)
00
, yx
, то уравнение параболы
()
(
)
0
2
0
2 xxpyy −=−
.
Эксцентриситет параболы
1
пар.
=
ε
.
Уравнение
0
22
=+++++ CByAxcybxyax
называется общим алгеб-
раическим уравнением второго порядка на плоскости.
Всякое алгебраическое уравнение второго порядка на плоскости опре-
деляет
1) эллипс, гиперболу, параболу;
или
2) прямую;
x
y
0
(
)
yxM ,
(
)
yxM ,
2p
2p−
