Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие
Подождите немного. Документ загружается.

§2. Линейная зависимость и независимость векторов
О п р е д е л е н и е. Векторы
n
ааа ,,,
21
K называются линейно за-
висимыми
, если существуют числа
n
λ
λ
λ
,,,
21
K
(не все равные 0), такие,
что
0
2211
=
⋅λ++⋅λ+⋅λ
nn
ааа K
, т.е. линейная комбинация векторов
обращается в ноль.
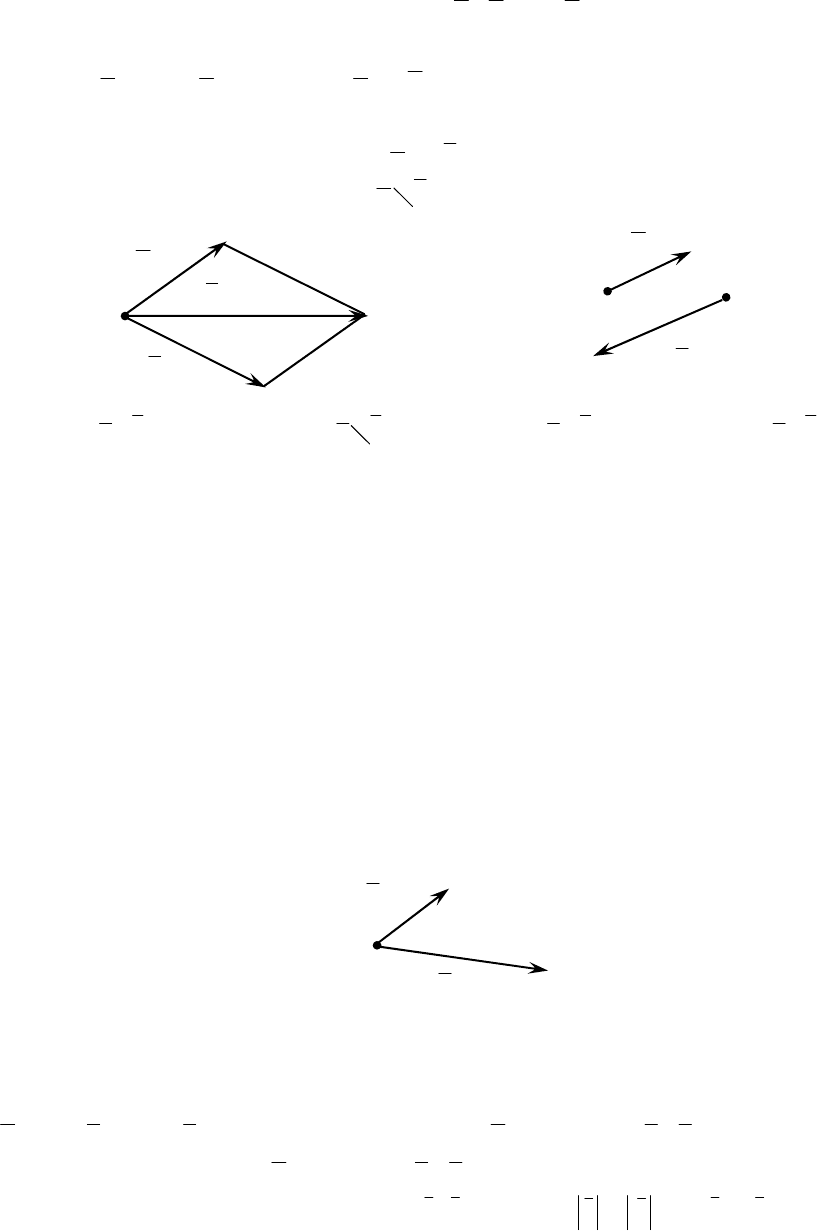
Два вектора на плоскости
а и b линейно независимы тогда и только
гда, когда они неколлинеарны:
ba ||
а , b – неколлинеарны ba || ; а , b – коллинеарны, ba || .
Рис. 5
Три вектора, имеющие общее начало называются компланарными,
если они лежат в одной плоскости или три произвольные вектора компла-
нарны, если они параллельны одной плоскости.
Три вектора в пространстве линейно независимы тогда и только то-
гда, когда они некомпланарны.
Базис и координаты
Базисом на плоскости называются любые два линейно независимых
вектора (любые два неколлинеарные вектора).
Рис. 6
Любой вектор на плоскости является линейной комбинацией базисных
векторов.
−
⋅λ+⋅λ=
2211
eea разложение вектора
a
по базису
(
)
21
, ee .
()
−λλ
21
, координаты a в базисе
(
)
21
, ee .
Стандартный базис на плоскости –
,, ji причем, 1
=
=
ji , ji ⊥ .
а
b
с
а
b
1
e
2
e
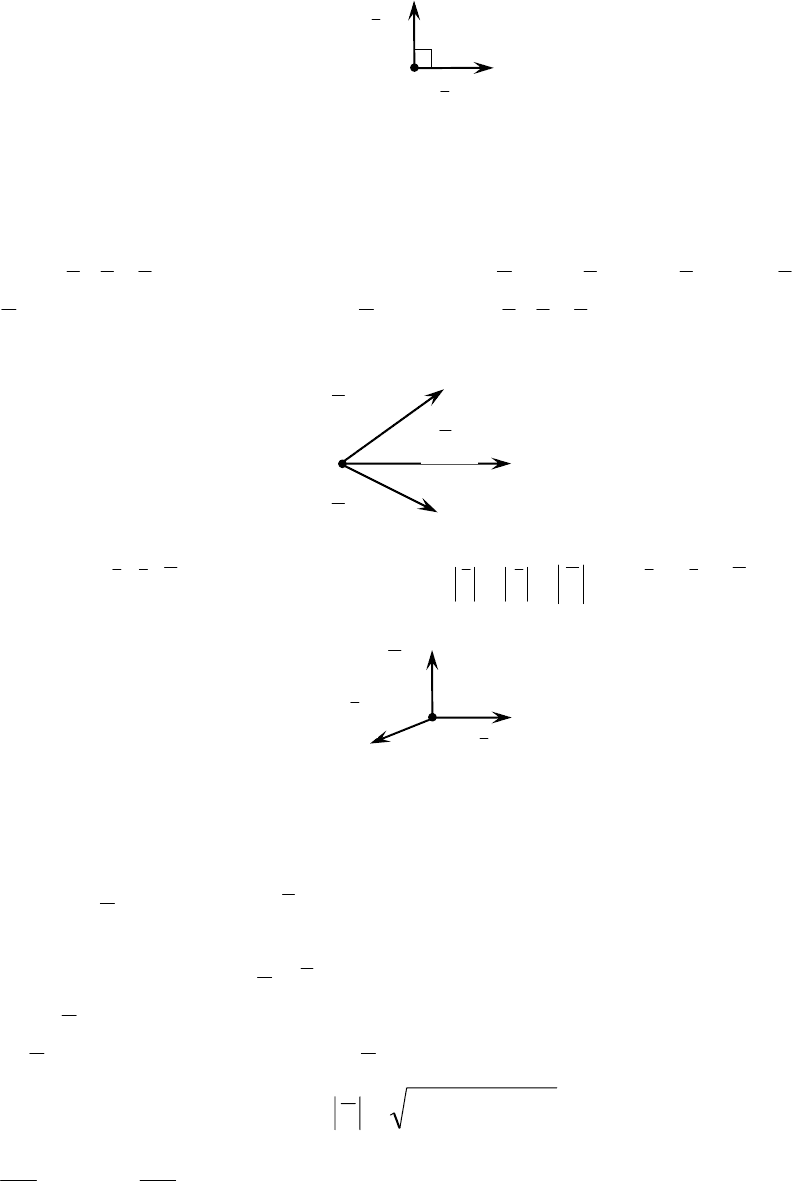
Рис. 7
Базис в пространстве − это любые три линейно независимые векто-
ра в пространстве. Любой вектор в пространстве является линейной ком-
бинацией базисных векторов.
Если
−
321
,, eee
базис в пространстве, то
332211
eeea ⋅λ+
⋅
λ
+
⋅
λ
=
.
()
−λλλ=
321
,,а координаты a в базисе
(
)
321
,, eee .
В пространстве базис образуют любые три некомпланарные векторы.
Рис. 8
Векторы −kji ,, стандартный базис: 1=== kji ; kji ⊥⊥ .
Рис. 9
Действия с векторами в координатной форме записи
1. Если
()
;,,
111
zyxа =
()
222
,, zyxb = координаты векторов, то сумма век-
торов – это вектор с координатами
()
212121
;; zzyyxxba +++=+ ;
2.
()
−⋅λ⋅λ⋅λ=⋅λ zyxa ;; умножение вектора на число
λ
.
3.
()
zyxa ,,=
. Длина вектора a находится по формуле
222
zyxa ++= ;
4.
()
;,,
111
zyxA =
()
222
,, zyxB = − две точки. Тогда координаты вектора
A
B равны:
(
)( )
(
)()
121212
;; zzyyxxAB −−−= .
3
e
1
e
2
e
k
j
i
j
i
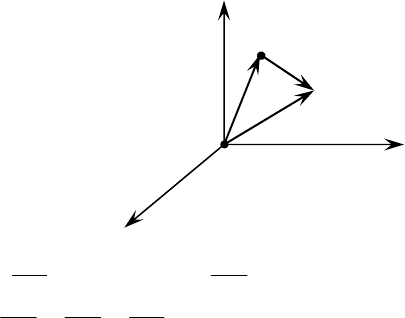
z
x
y
0
A
B
Рис. 10
Действительно:
()
;,,
111
zyxOA =
(
)
222
,, zyxOB = ;
(
)
(
)
(
)
(
)
121212
;; zzyyxxOAOBAB −−−=−= .
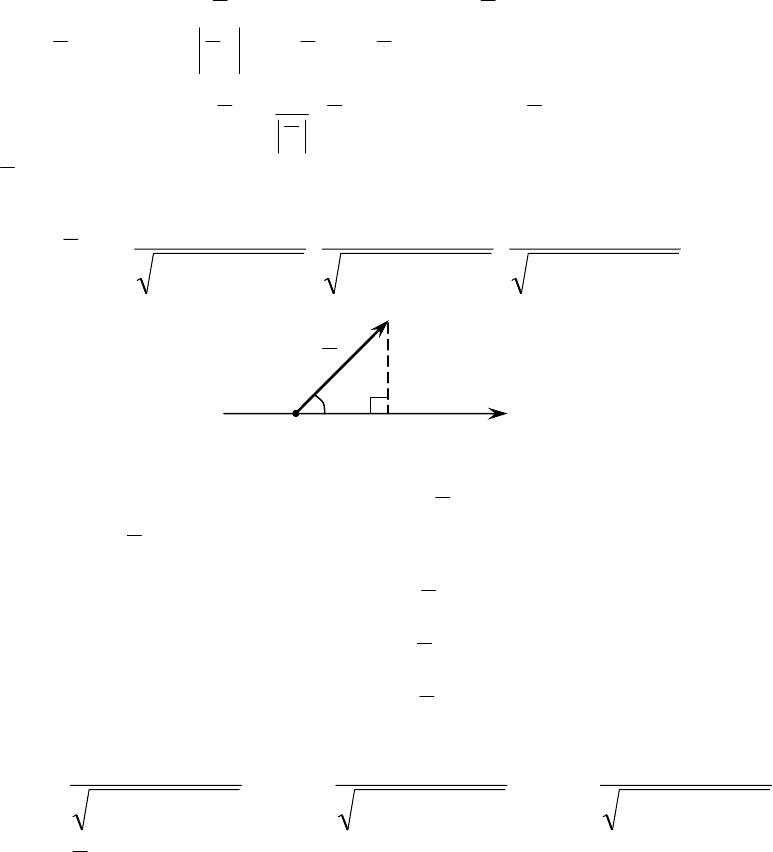
α
a
§3. Орт и направляющие косинусы
Ортом вектора
a
называется вектор
о
а имеющий тоже направле-
ние что и
a и модуль 1
о
=а ;
аа
↑
↑
о
.
а
а
а ⋅=
1
о
− орт вектора
a
.
Если
()
zyxа ,,= , то координаты орта находятся по формуле
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
++++++
=
222222222
о
;;
zyx
z
zyx
y
zyx
x
а .
Рис. 11
Направляющие косинусы вектора a − это косинусы углов ,,,
γ
β
α
которые вектор
a образует с осями координат.
()
()
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=γ
=β
=α
∧
∧
∧
.O,coscos
;O,coscos
;O,coscos
za
ya
xa
;cos;cos;cos
222222222
zyx
z
zyx
y
zyx
x
++
=γ
++
=β
++
=α
Затем, что
()
γβα= cos,cos,cos
o
a
, т.е. координата орта равна направляю-
щим косинусам.
Основное свойство косинусов: 1coscoscos
222
=γ+β+α .
0
x
x
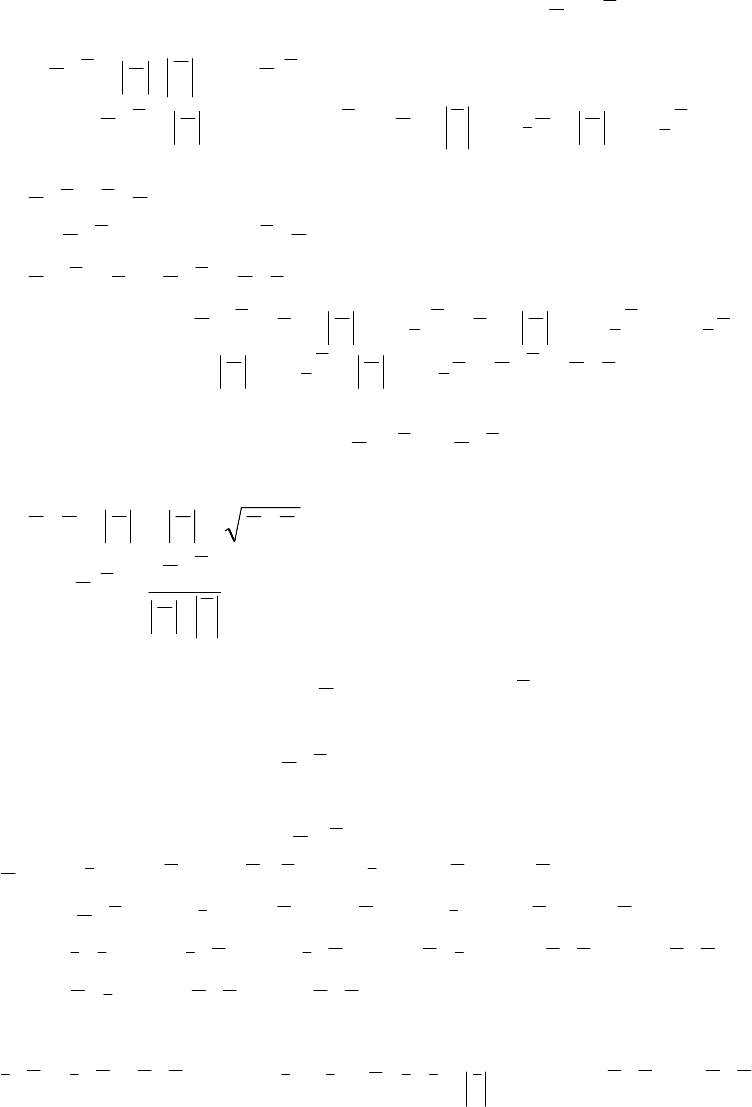
§4. Скалярное произведение векторов
Скалярным произведением векторов
a и b называется число, рав-
ное
()
∧
⋅⋅=⋅ bababа ,cos
,
или
(
)
baabababa
a
b
ПрПр на проекция ⋅=⋅=⋅=⋅
.
Свойства:
1.
abba ⋅=⋅ (коммутативность);
2.
()
(
)
abba ⋅⋅β⋅α=β⋅⋅⋅α (сочетательность);
3.
(
)
cabacba ⋅+⋅=+⋅ (дистрибутивность),
Действительно,
(
)
(
)
(
)
=+⋅=+⋅=+⋅ cbacbacba
aaa
ПрПрПр
cabacaba
aa
⋅+⋅=⋅+⋅= ПрПр .
Критерий перпендикулярности
(
)
⊥
векторов:
0
=
⋅
⇔
⊥
baba .
Основное использование:
1.
;
2
aaa =⋅
aaa ⋅=
− нахождение длины вектора;
2.
()
ba
ba
ba
⋅
⋅
=
∧
,cos − нахождение угла между векторами.
Вычисление скалярного произведения:
Т е о р е м а.
Если
(
)
111
,, zyxa = и
(
)
222
,, zyxb = − два вектора, то
их скалярное произведение находится по формуле
212121
zzyyxxba ⋅+⋅+⋅=⋅ .
Доказательство:
Запишем векторы a , b в виде линейной комбинации базисных:
kzjyixa ⋅+⋅+⋅=
111
, kzjyixb ⋅+⋅+⋅=
222
.
Тогда
(
)
(
)
=⋅+⋅+⋅⋅⋅+⋅+⋅=⋅ kzjyixkzjyixba
222111
+⋅+⋅+⋅+⋅+⋅+⋅= kjzyjjyyijxykizxjiyxiixx
212121212121
212121212121
zzyyxxkkzzjkyzikxz ++=⋅+⋅+⋅+ .
Здесь использованы скалярные произведения базисных векторов:
0=⋅=⋅=⋅ kjkiji , т. к. kji ⊥⊥ ;
;11
2
2
===⋅ iii
1=⋅ jj ; 1=⋅
k
k
.
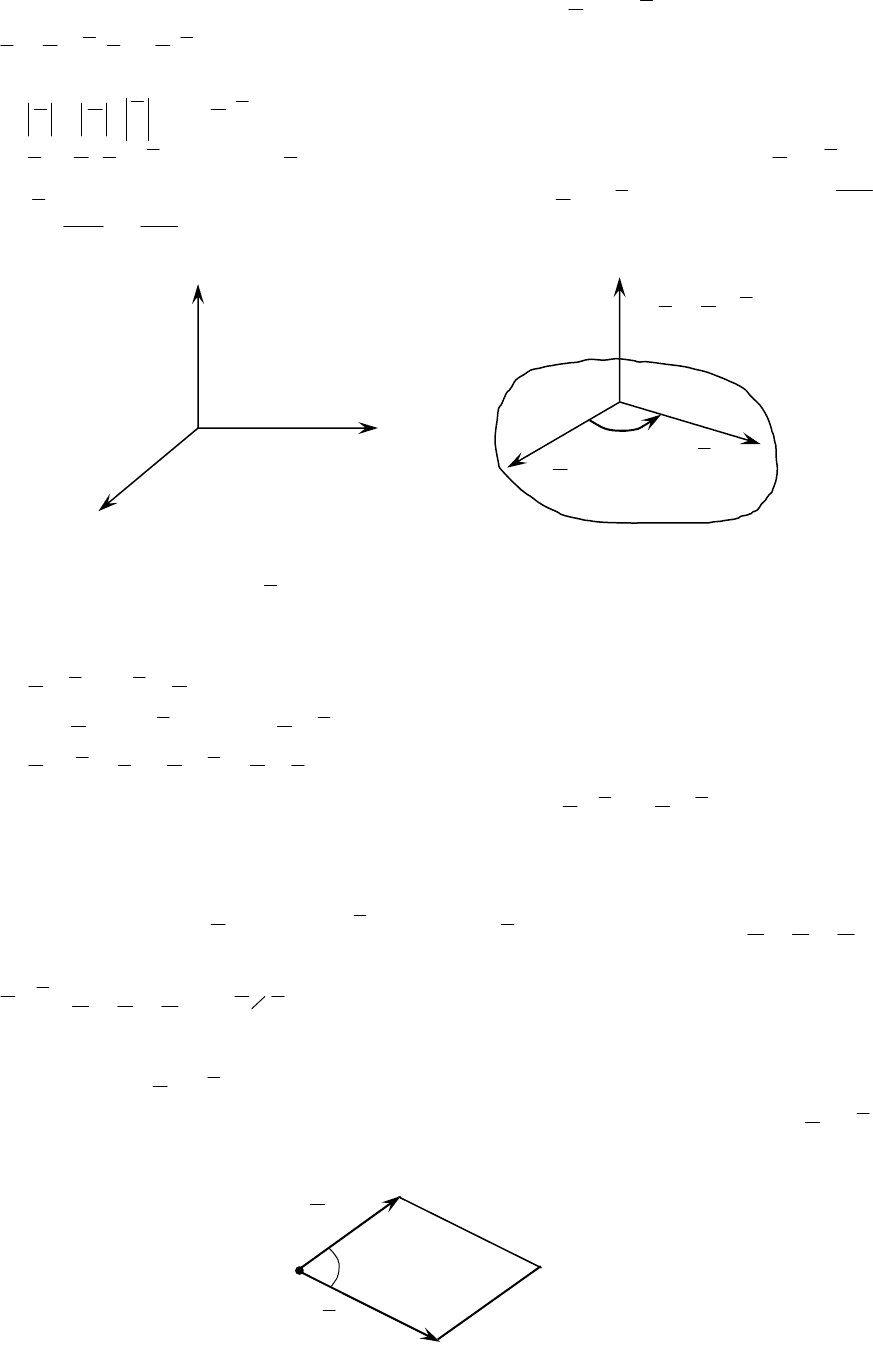
z
x
y
0
§5. Векторное произведение векторов
Векторным произведением векторов
a и b называется вектор
[
]
(
)
bacbac ,=×= , удовлетворяющий условиям:
1.
()
∧
⋅⋅= babac ,sin
− длина векторного произведения;
2. bcaс ⊥⊥ , − вектор
с
перпендикулярен плоскости векторов
a
и b ;
3. с расположен по отношению к векторам a и b также, как ось OZ к
осям
O
X
и O
Y
.
Рис. 12
Направление вектора с определяется правилом буравчика (правило бурав-
чика).
Свойства:
1.
(
)
abba ×−=× (антикоммутативность);
2.
()
(
)
(
)
baba ×⋅β⋅α=⋅β×⋅α (сочетательность);
3.
(
)
cabacba ×+×=+×
(дистрибутивность).
4. Т е о р е м а (критерий коллинеарности): 0|| =×⇔ baba .
З а м е ч а н и е. Если известны координаты векторов, то для про-
верки их коллинеарности проверяется пропорциональность координат.
Например:
()
,4;1;3=a
(
)
8;2;6=b ,
(
)
8;3;6
=
c . Так как
8
4
2
1
6
3
== , то
ba || ;
8
4
3
1
6
3
≠≠ , то ca || .
5. Т е о р е м а (геометрический смысл векторного произведения):
Пусть
a и b имеют общее начало. Тогда длина векторного произве-
дения векторов равна площади параллелограмма, построенного на
a и b .
Доказательство.
baс ×
=
a
b
а
b
S
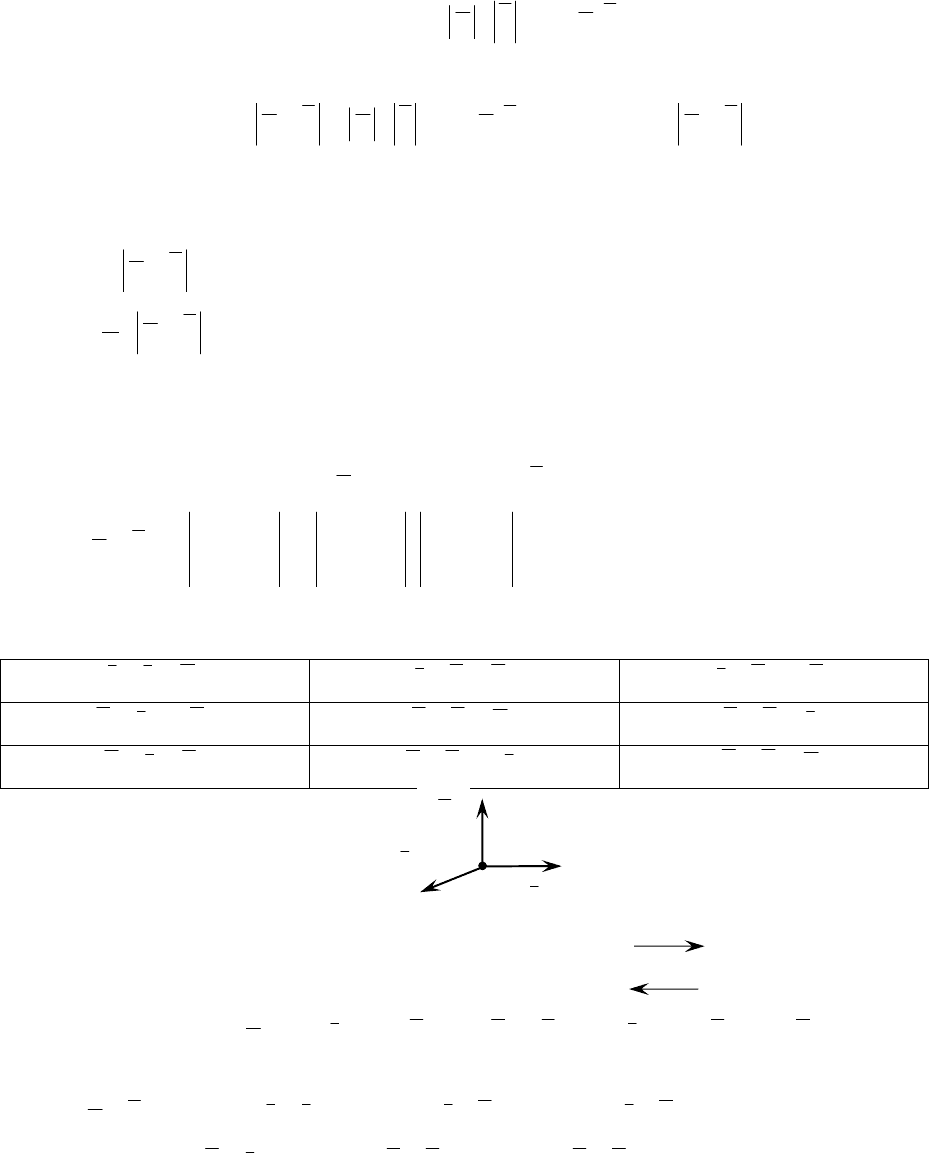
Рис. 13
Вспомним формулу площади параллелограмма:
()
∧
⋅⋅= babaS ,sin
пар.
.
Заметим, что по свойству (1):
()
∧
⋅⋅=× bababa ,sin , т. е. baS ×=
.пар
Формулы для приложений
1. baS ×=
.пар
;
2. baS ×⋅=
∆
2
1
.
Выражение векторного произведения векторов через их коорди-
наты.
Т е о р е м а.
Пусть:
(
)
111
,, zyxa = и
(
)
222
,, zyxb = .
Тогда
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=×
22
11
22
11
22
11
;;
yx
yx
zx
zx
zy
zy
ba .
Доказательство.
Составим таблицу:
0=×ii ;
kji =× ; jki −=× ;
kij −=× ; 0=× jj ; ikj =× ;
jik =× ; ijk −=× ;
0=×
k
k
.
Рис. 14
Для запоминания таблицы удобна «шпаргалка»: ji
k
ji .
Докажем теорему:
По условию:
kzjyixa ⋅+⋅+⋅=
111
и kzjyixb ⋅+⋅+⋅=
222
.
Имеем:
()
(
)
(
)
+×⋅⋅+×⋅⋅+×⋅⋅=× kizxjiyxiixxba
211121
(
)
(
)
(
)
+×⋅⋅+×⋅⋅+×⋅⋅+ kjzyjjyyijxy
212121
k
j
i
−
+
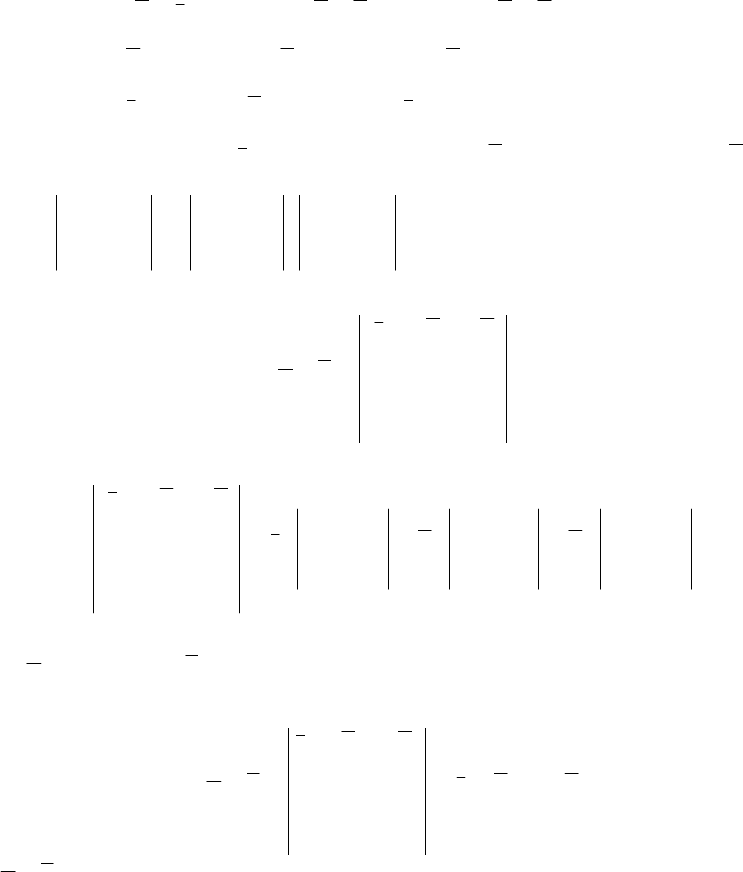
(
)
(
)
(
)
=×⋅⋅+×⋅⋅+×⋅⋅+ kkzzjkyzikxz
212121
(
)
(
)
+−⋅⋅+−⋅⋅+⋅⋅= kxyjzxkyx
212121
(
)
=−⋅⋅+⋅⋅+⋅⋅+ iyzjxzizy
212121
(
)
(
)
(
)
=⋅⋅−⋅+⋅⋅+⋅−+⋅⋅−⋅= kxyyxjxzzxiyzzy
212121212121
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
22
11
22
11
22
11
;;
yx
yx
zx
zx
zy
zy
.
С л е д с т в и е.
222
111
zyx
zyx
kji
ba
=× .
Доказательство.
22
11
22
11
22
11
222
111
yx
yx
k
zx
zx
j
zy
zy
i
zyx
zyx
kji
⋅+⋅−⋅= .
Пример.
Пусть
()
0;1;1 −=a ,
()
1;1;2 −=b − координаты двух векторов.
Тогда
kji
kji
bа ⋅++=
−
−=× 3
112
011;
т. е.
()
3;1;1=× ba .
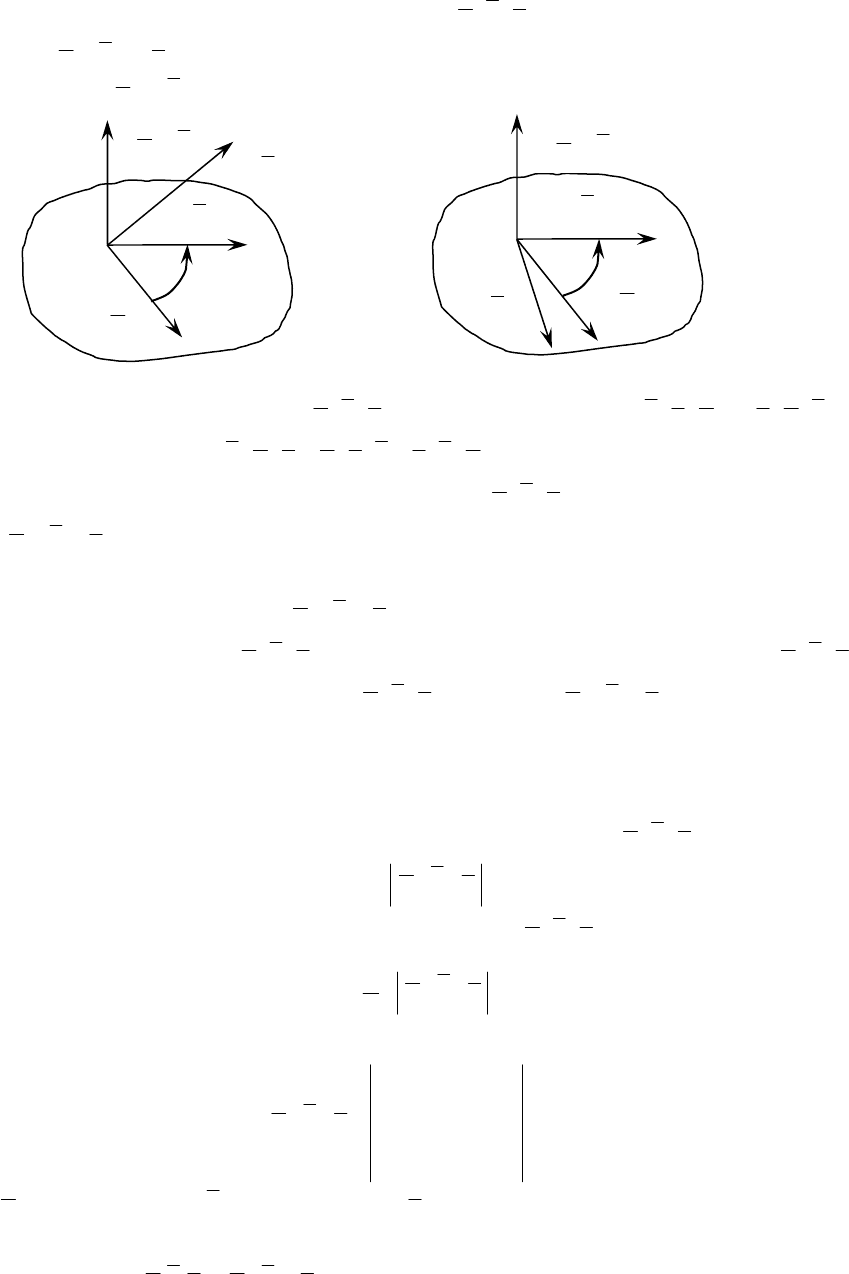
§6. Смешанное произведение векторов
Тройка некомпланарных векторов
cba ,, называется правой, если
векторы
ba × и c расположены по одну и ту же сторону плоскости, пове-
дённой через
a и b .
Рис. 15
З а м е ч а н и е. Если cba ,, − правая тройка, то aсb ,, и bac ,, −
тоже правые, а тройки
cab ,,; bca ,,; abc ,, − левые.
Смешанным произведением векторов
cba ,, называется число, рав-
ное
(
)
cba ⋅× .
Т е о р е м а (геометрический смысл смешанного произведения):
Смешанное произведение
(
)
cba ⋅× равно объёму параллелепипеда, по-
строенного на векторах
cba ,,, взятого со знаком плюс, если тройка cba ,,
− правая, и со знаком минус, если cba ,, − левая.
(
)
(
)
Vcba ±=⋅× .
Формулы для приложений
1. Объём параллелепипеда, построенного на векторах cba ,,:
cbaV
пар
⋅⋅=
.
.
2. Объём пирамиды, построенной на векторах cba ,,:
cbaV ⋅⋅⋅=
∆
6
1
.
Вычисление смешанного произведения в координатах:
,
ccc
bbb
aaa
zyx
zyx
zyx
cba =⋅⋅
где
{}
;,,
aaa
zyxa =
{}
;,,
bbb
zyxb =
{
}
ccc
zyxc ,,
=
− координаты векто-
ров.
Действительно,
cbacba ×⋅= .
ba
×
a
b
с
a
b
ba
×
с
правая
тройка
левая
т
р
ойк
а
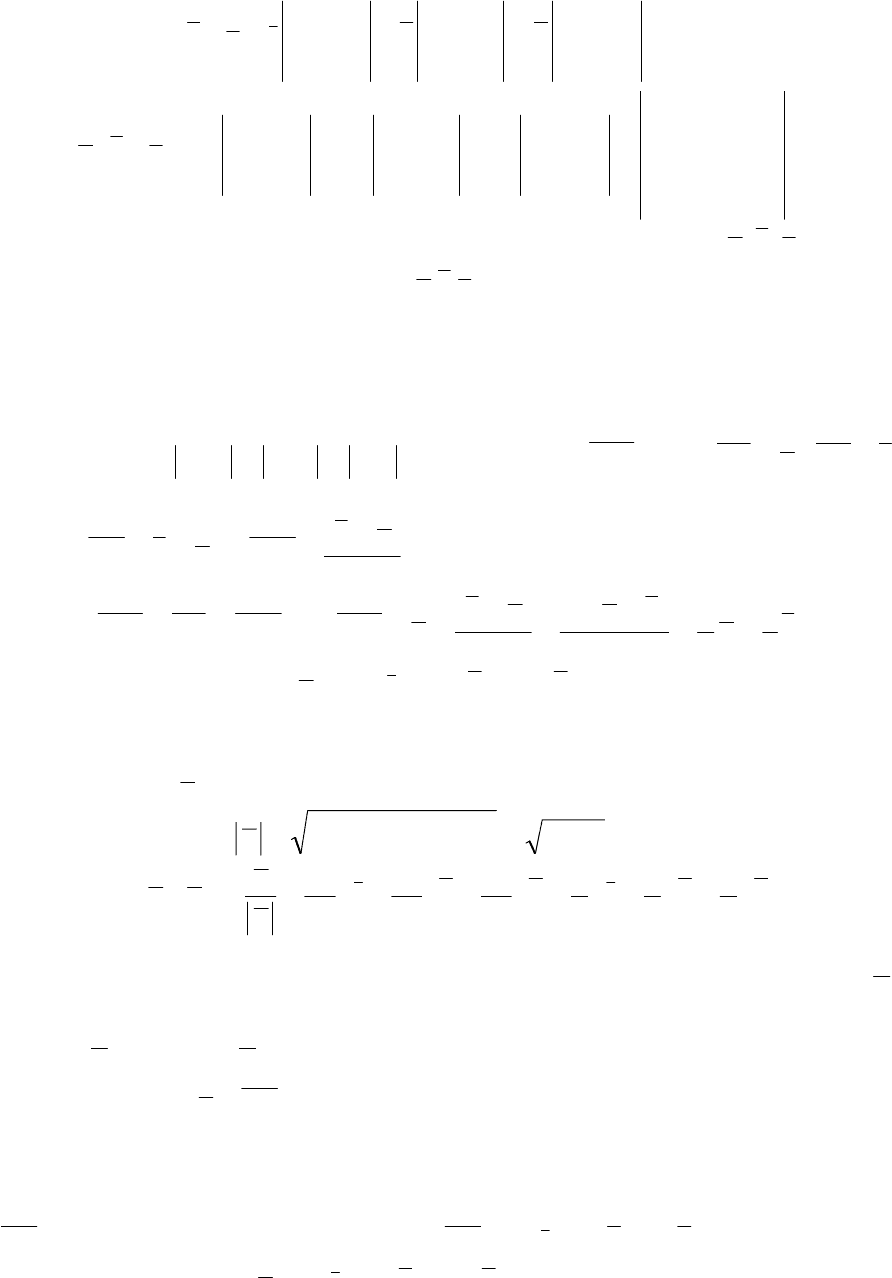
По теореме §5:
cc
bb
cc
bb
cc
bb
yx
yx
k
zx
zx
j
zy
zy
icb +−=× .
Тогда
ccc
bbb
aaa
cc
bb
a
cc
bb
a
cc
bb
a
zyx
zyx
zyx
yx
yx
z
zx
zx
y
zy
zy
xcba =+−=×⋅ .
Т е о р е м а (критерий компланарности). Векторы cba ,, компла-
нарны тогда и только тогда, когда
0=cba .
Примеры решения задач
1. В треугольнике
A
B
C
сторона
A
B точками
M
и
N
разделена на три
равные части:
NBMNAM == . Найти вектор ,СM если ,aCA = .bCB
=
Решение:
Имеем
(
)
3
ab
AMabAB
−
=⇒−= .
Так как
A
MCAСM
+
= , то
(
)
(
)
ba
baab
aCM
3
1
3
2
3
2
3
+=
+⋅
=
−
+= .
2. Найти длину вектора kjia ⋅−⋅+⋅= 603020 и его направляющие коси-
нусы.
Решение:
Найдем длину a :
704900603020
222
==++=a .
Найдём орт
a : kjikji
a
a
a
o
⋅−⋅+⋅=⋅−⋅+⋅==
7
6
7
3
7
2
70
60
70
30
70
20
.
Координаты вектора равны направляющим косинусам, поэтому
;
7
2
cos =α
;
7
3
cos =
β
7
6
cos −=
γ
.
3. Найти вектор
A
Ba
=
, если
(
)
2,3,1A и
(
)
1,8,5
−
B .
Решение:
Чтобы найти координаты вектора, нужно из координат точки-конца вы-
честь координаты начала:
{}{}
kjiABAB ⋅−⋅+⋅=⇒−=−−−−= 3543;5;421;38;15.
4. Найти орт вектора kjia ⋅−⋅+⋅= 1243.
Решение:
