Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие
Подождите немного. Документ загружается.

.0
101
512
111
=
+
−
− zyx
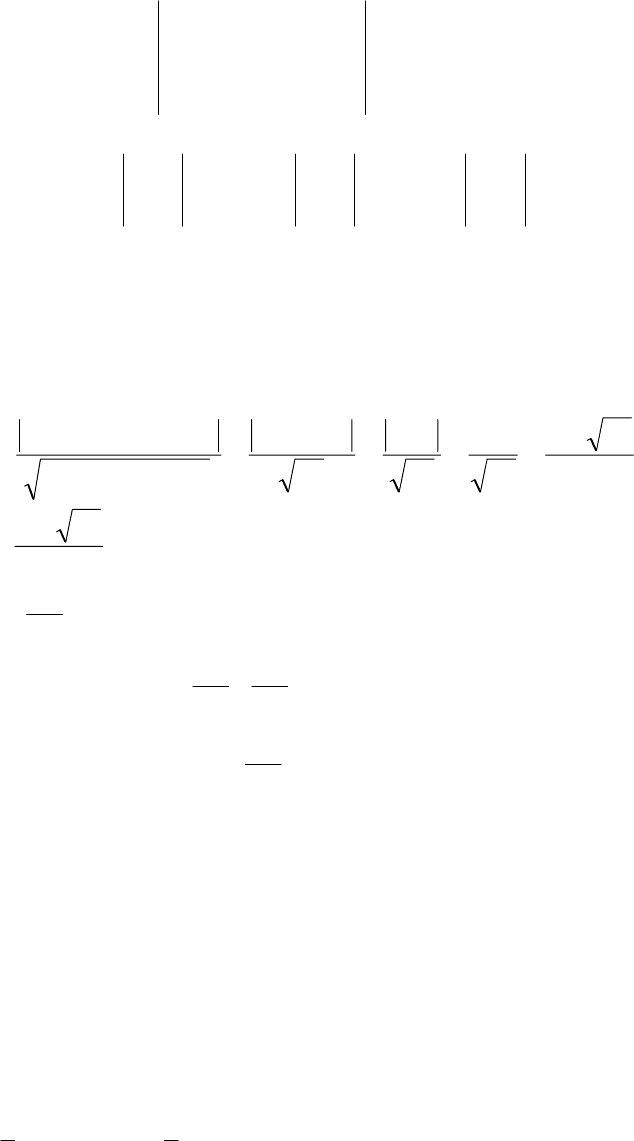
Вычисляем определитель, раскладывая по 1-ой строке:
() () ()
;0
01
12
1
11
52
1
10
51
1 =⋅++⋅−−⋅− zyx
()
(
)
(
)
(
)
;0111311
=
+
⋅
−
−
⋅
−
−−⋅ zyx
;01331
=
−
−
−
⋅
+
−
z
y
x
053 =−−⋅+
z
y
x
− уравнение плоскости, проходящей через точки
321
,, MMM
.
Теперь используем формулу расстояния от точки до плоскости
()
α :
()
()
11
1113
11
13
11
13
11
692
131
51332
2
22
⋅
==
−
=
−−
=
−++
−−−⋅+
=d
.
Ответ:
11
1113 ⋅
− расстояние от
0
M
до плоскости
α
.
2. Написать уравнение плоскости, проходящей через точку
A
перпендику-
лярно вектору
BC
, если
()
(
)
(
)
2;1;1,4;1;3,2;3;2
−
CBA
.
Решение:
Найдём координаты вектора
BC
:
{
}
{
}
2;2;242;11;31 −−−=−−−−=BC
.
Получившиеся числа являются коэффициентами перед
zy
x
,,
в уравнении
плоскости
α
, перпендикулярной
B
C
:
(
)
0222: =+
⋅
−
⋅
−
⋅
−
α
Bzyx .
По условию точка
A
принадлежит ⇒
α
координаты
A
удовлетворяют урав-
нению плоскости:
0223222
=
+
⋅
−
⋅
−
⋅− B
;
0464
=
+
−
−
−
B ;
14
=
B
.
Уравнение
()
014222:
=
+
⋅
−⋅−⋅−α zyx
или
07
=
−
+
+
z
y
x
.
Ответ:
()
014222:
=
+
⋅
−
⋅−⋅
−
α zyx
или
07 =
−
+
+
zy
x
.
3. Найти угол между плоскостями
043
=
−
⋅
+
−
z
y
x
и
082 =+−
+
⋅
z
y
x
.
Решение:
Угол между плоскостями совпадает с углом между их нормалями. Нормали
плоскостей:
{}
{
}
.1,1,2;3,1,1
21
−
=
−
= nn
Угол между нормалями найдём с помощью скалярного произведения:
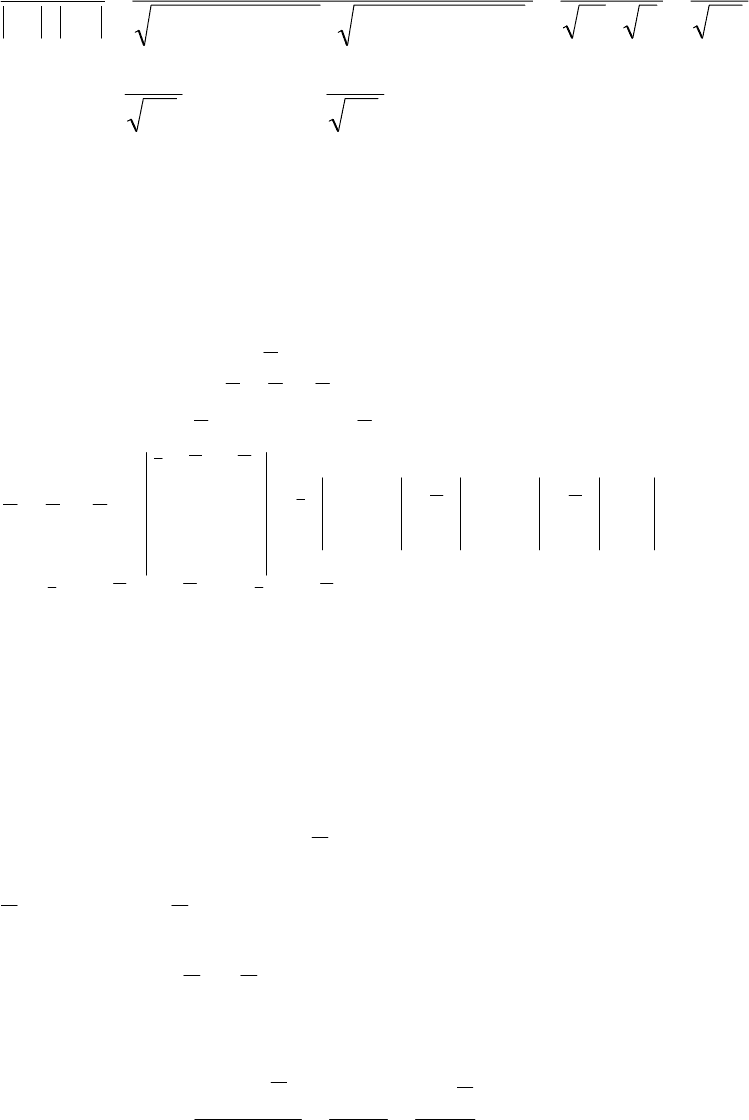
(
)
(
)
()
()
66
2
611
2
112311
131112
cos
2
222
2
2
21
21
−
=
⋅
−
=
−++⋅+−+
−
⋅
+
−
⋅
+
⋅
=
⋅
⋅
=γ
ПП
ПП
.
Ответ:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=γ
−
=γ
66
2
arccos;
66
2
cos
.
6. Написать каноническое уравнение прямой
⎩
⎨
⎧
=−++
=
+
⋅
−
+
.01
;043
zyx
zyx
Решение:
Чтобы составить каноническое уравнение прямой, необходимо найти её на-
правляющий вектор и точку на прямой.
Направляющий вектор прямой
a находим как векторное произведение век-
торов-нормалей плоскостей:
.
21
nna
×
=
{
}
{
}
1,1,1;3,1,1
21
=
−
= nn
.
=⋅+
−
⋅−
−
⋅=−=×=
11
11
11
31
11
31
111
311
21
kji
kji
nna
{
}
0;4;444044 −=⋅−⋅=⋅+⋅−⋅= jikji
.
Найдём какую-нибудь точку на прямой. Положим, например,
0=y
. Тогда
получим систему:
⎩
⎨
⎧
=−+
=
+
⋅
−
;01
;043
zx
zx
;054
=
+
⋅
−
z
.
4
5
=z
Тогда
;01
4
5
=−+x
.
4
1
−=x
Итак, получили точку
⎟
⎠
⎞
⎜
⎝
⎛
−
4
5
;0;
4
1
.
Составляем каноническое уравнение прямой:
;
0
4
5
4
0
4
4
1
−
=
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−−
z
y
x

.
0
4
5
44
4
1
−
=
−
=
+ z
y
x
Ответ: .
0
4
5
44
4
1
−
=
−
=
+ z
y
x
.
7. Найти точку пересечения прямой и плоскости:
;
1
3
4
1
2
1
−
=
−
=
+
zyx
.012
=
−
+
⋅
−
z
y
x
Решение:
Запишем уравнение прямой в параметрическом виде:
⇒=
−
=
−
=
+
t
zyx
1
3
4
1
2
1
⎪
⎩
⎪
⎨
⎧
=−
⋅=−
⋅
=
+
;3
;41
;21
tz
ty
tx
⎪
⎩
⎪
⎨
⎧
+=
+⋅=
−
⋅
=
.3
;14
;12
tz
ty
tx
Подставляем эти выражения в уравнение плоскости:
()
(
)
(
)
01314212
=
−
+
+
+
⋅
⋅
−−⋅ ttt
;
0132812
=
−
+
+
−
⋅
−−⋅
t
t
t
;
015
=
−⋅−
t
;
5
1
−=t .
Подставляем в систему:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=+−=
=+
⎟
⎠
⎞
⎜
⎝
⎛
−⋅=
−=−
⎟
⎠
⎞
⎜
⎝
⎛
−⋅=
.
5
14
3
5
1
;
5
1
1
5
1
4
;
5
7
1
5
1
2
z
y
x
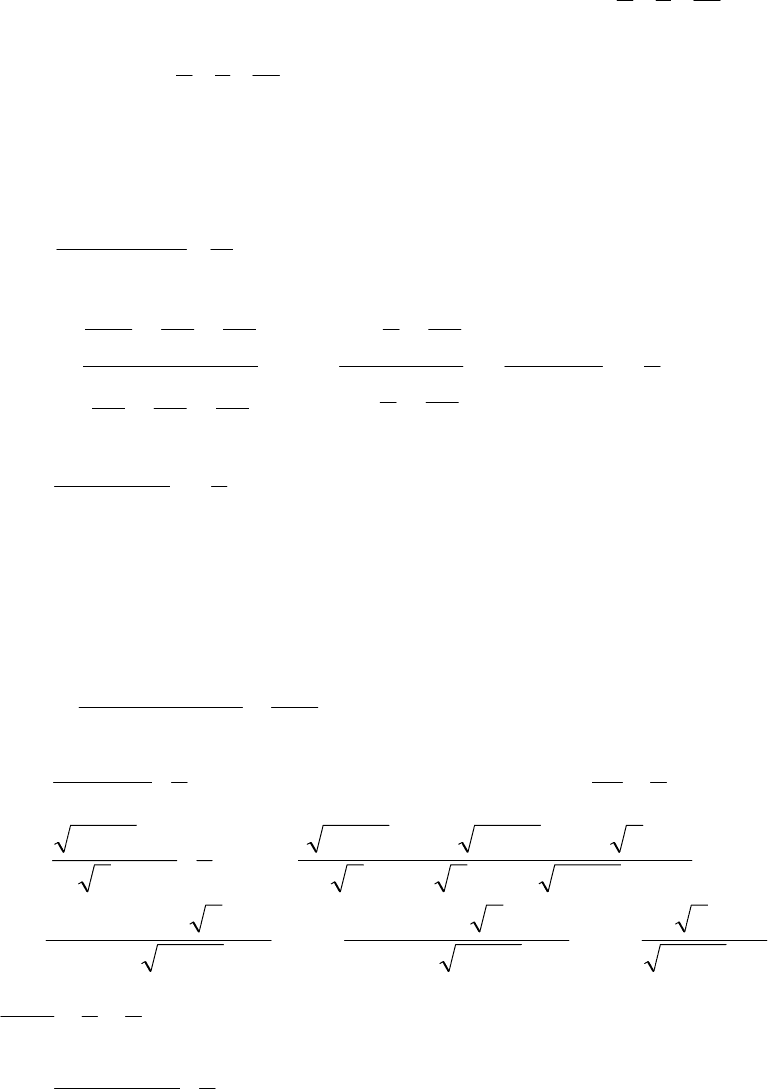
Итак, нашли координаты точки пересечения:
⎟
⎠
⎞
⎜
⎝
⎛
−
5
14
;
5
1
;
5
7
.
Ответ:
⎟
⎠
⎞
⎜
⎝
⎛
−
5
14
;
5
1
;
5
7
.
Часть 4
а)
=
⎟
⎠
⎞
⎜
⎝
⎛
∞
∞
+−
−+
∞→
6
74
lim
2
2
xx
xx
x
(делим числитель и знаменатель на
2
x
)
4
1
4
001
004
61
1
71
4
lim
6
74
lim
2
2
222
2
222
2
==
⎟
⎠
⎞
⎜
⎝
⎛
+−
−+
=
+−
−+
=
+−
−+
=
∞→∞→
x
x
x
x
x
x
x
x
x
xx
x
x
x
xx
;
б)
=
⎟
⎠
⎞
⎜
⎝
⎛
=
−−
−
→
0
0
2
82
lim
2
2
2
xx
x
x
Раскладываем числитель и знаменатель на множители
(
)
(
)
(
)
2224282
22
+−⋅=−⋅=− xxxx
;
02
2
=
−
−
x
x
;
1
1
=
x
;
2
2
=
x
.
()()
()( )
8
1
42
21
222
lim
2
=
⋅
=
−−
+
−
=
→
xx
xx
x
;
в)
()
2
1
6
3
lim6~6arcsin;3~3sin
0
0
6arcsin
3sin
lim
00
===
⎟
⎠
⎞
⎜
⎝
⎛
→→
x
x
xxxx
x
x
xx
;
г)
(
)
(
)
(
)
()()()
=
++⋅+⋅−
+⋅++⋅−+
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−+
→→
32122
2321321
lim
0
0
2
321
lim
44
xxx
xxx
x
x
xx
()
(
)
()
()
(
)
(
)
()
()
(
)
=
++
+
=
++⋅−
+⋅−
=
++⋅−
+⋅−+
=
→→→
321
22
lim
3214
242
lim
3214
2921
lim
444
x
x
xx
xx
xx
xx
xxx
3
4
6
8
33
42
==
+
⋅
=
;
д)
()
=
⎟
⎠
⎞
⎜
⎝
⎛
+
→
0
0
4sin
sin1ln
lim
0
x
x
x
Используем эквивалентности
(
)
α
α
+
~1ln
,
α
α
~
sin
при
0→
α
, получим

4
1
4
lim
0
0
4
sin
lim
00
==
⎟
⎠
⎞
⎜
⎝
⎛
→→
x
x
x
x
xx
;
е)
()()
=
−+
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
→→
11ln
1
lim
0
0
ln
1
lim
2
1
2
1
x
x
x
x
xx
Используем эквивалентность
(
)
(
)
(
)
xx
−
−
+
1~11ln , т.к.
(
)
01 →
−
x при 1→
x
,
получим
()()
()
()
21lim
1
11
lim
11
=+=
−
+−
=
→→
x
x
xx
xx
.
НЕОБХОДИМО УМЕТЬ
Линейная алгебра
1. Вычислять определитель.
2. Складывать, перемножать, транспонировать матрицы.
3. Вычислять миноры, алгебраические дополнения.
4. Находить обратную матрицу.
5. Решать матричные уравнения.
6. Решать системы линейных уравнений матричным методом, методом
Крамера, Гаусса.
Векторная алгебра
1. Производить действия с геометрическими векторами.
2. Находить длину, орт, направляющие косинусы вектора.
3. Вычислять скалярные, векторные, смешанные
произведения векторов.
4. Находить расстояния, площади треугольника, параллелограмма, объем
параллелепипеда, решать геометрические задачи.
Аналитическая геометрия
1. Находить расстояние между точками.
2. Проводить прямую через две точки, через точку параллельно
(перпендикулярно, под углом) к данной прямой.
3. Вычислять угол между прямыми. Находить точку пересечения прямых,
расстояние от точки до прямой.
4. Приводить
к каноническому виду, строить эллипс, гиперболу, параболу.
5. Проводить плоскость через три точки, через прямую и точку, через две
параллельные прямые.
6. Находить расстояние от точки до плоскости, находить проекцию точки на
плоскость.
7. Прямая в пространстве, по двум точкам. Угол между прямыми в
пространстве, приводить уравнение к каноническому виду.
8. Находить угол
между прямой и плоскостью, точку пересечения прямой и
плоскости.
Математический анализ
1. Вычислять пределы последовательностей.
2. Вычисление пределов функций, различные типы неопределенностей.
Пределы в точке и на бесконечности.
3. Использование замечательных пределов, эквивалентностей бесконечно –
малых.
4. Нахождение односторонних пределов.
5. Исследование точек разрыва.
ВОПРОСЫ К ЭКЗАМЕНУ
1. Матрицы и действия с ними.
2. Определители, их свойства и вычисление. Миноры, алгебраические дополнения.
3. Определение, существование, вычисление обратной матрицы.
4. Крамеровские системы линейных уравнений, их решение по формулам Крамера и
матричным методом.
5. Решение систем методом Гаусса.
6. Понятие вектора, арифметические операции с векторами, их свойства.
7. Проекция вектора
на ось, основная теорема о проекциях.
8. Базис и координаты вектора, на плоскости и в пространстве, действия с векторами в
координатной форме записи.
9. Скалярное произведение векторов, его основные свойства, критерий
перпендикулярности, применение.
10. Выражение скалярного произведения через координаты векторов.
11. Векторное произведение векторов, его основные свойства, критерий коллинеарности,
использование.
12. Выражение векторного
произведения через координаты векторов.
13. Смешанное произведение векторов, его геометрический смысл, вычисление.
14. Уравнение прямой с угловым коэффициентом, угол между прямыми, ус-
ловие параллельности, перпендикулярности.
15. Общее уравнение прямой, уравнение прямой в отрезках, пара прямых на плоскости.
16. Кривые второго порядка: эллипс, гипербола, парабола.
17. Общее уравнение плоскости, его частные виды, уравнение плоскости
в отрезках.
18. Угол между плоскостями, плоскость, проходящая через 3 точки, расстояние от точки
до плоскости.
19. Уравнения прямой в пространстве: каноническое, параметрическое, как пересечение
прямых и плоскостей.
20. Взаимное расположение прямых и плоскостей в пространстве.
21. Понятие функции, сложной функции.
22. Предел числовой последовательности.
23. Бесконечно – малые последовательности, их связь с бесконечно – большими
последовательностями.
24. Основные свойства последовательностей, имеющих предел.
25. Понятие предела функции в точке и на бесконечности.
26. Основные свойства предела функции.
27. Замечательные пределы.
28. Сравнение бесконечно – малых функций, эквивалентные бесконечно – малые
функции, их использование.
29. Непрерывность функции в точке, основные свойства непрерывных функций.
30. Точки разрыва графика функции, их классификация.
31. Определение производной, геометрический
смысл, уравнение касательной.
32. Основные свойства производной.
33. Производные элементарных функций.
34. Производная сложной функции, производные от функций, заданных неявно,
параметрически. Производные высших порядков.
35. Дифференциал функции.
36. Теоремы Веерштрасса о наибольшем и наименьшем значениях функции на отрезке,
Коши о промежуточных значениях, Ферма, Ролля, Лагранжа. Их геометрический смысл..
37. Исследование функции с помощью производных: монотонность, экстремумы,
выпуклость, перегибы.
38. Асимптоты графика функции.
39. Схема исследования функции, построение графика.
40. Формула Тейлора.
ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ
КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных
работ необходимо придерживаться указанных ниже
правил. Работы, выполненные без соблюдения этих правил, не засчитываются и
возвращаются студенту для переработки.
1. Номер варианта для выполнения контрольной работы выбирается по двум
последним цифрам шифра студента. Так как в каждом задании содержится 30 вариантов,
то номер варианта контрольной работы определяется так: а) если две последние
цифры
шифра 37, то будет 7-й вариант: 37-30=7; б) если две последние цифры шифра 79, то
будет 19-й вариант: 79-30х2=19 и т.д.
2. Каждая контрольная работа должна быть выполнена в отдельной тетради в
клетку чернилами любого цвета, кроме красного. Необходимо оставлять поля шириной
4-5см для замечаний рецензента.
3. В заголовке работы на обложке
тетради должны быть ясно написаны фамилия
студента, его инициалы, учебный номер (шифр), название дисциплины, номер
контрольной работы, здесь же следует указать название учебного заведения, дату
отсылки работы в институт и адрес студента. В конце работы следует поставить дату её
выполнения и подпись студента.
4. В работу должны быть включены все задачи
, указанные в задании, строго по
полагающемуся варианту. Контрольные работы, содержащие не все задачи задания, а
также задачи не своего варианта, не засчитываются.
5. Решения задач надо располагать в порядке возрастания их номеров, указанных в
заданиях, сохраняя номера задач.
6. Перед решением каждой задачи надо полностью выписать её условие. Решения
задач следует
излагать подробно и аккуратно, объясняя все действия по ходу решения и
делая необходимые чертежи.
7. После получения прорецензированной работы, как не зачтенной, так и
зачтенной, так и зачтённой условно, студент должен исправить все отмеченные
рецензентом ошибки и недочёты и прислать работу ещё раз. В случае незачёта работы и
отсутствия прямого указания
о том, что студент может ограничиться представлением
исправленных решений отдельных задач, вся работа должна быть выполнена заново.
8. Зачтённые контрольные работы предъявляются студентам при сдаче зачёта и
экзамена.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и
учащихся вузов. - М.: Наука, 1980. - С 246-259
2. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. - М.:
Наука, 1984. - С. 136-181
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и
задачах. М.: Высшая
школа, 1986. – Т.1., 304 с.
4. Мышкис А.Д. Лекции по высшей математике. - М.:
Наука, 1969. - С. 170-180, 274-281.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления – М.:
Наука, 1985. Т.1., 430 с.
6. Фадеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. М.:
Наука, 1968. - С. 21-82.
