Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие
Подождите немного. Документ загружается.

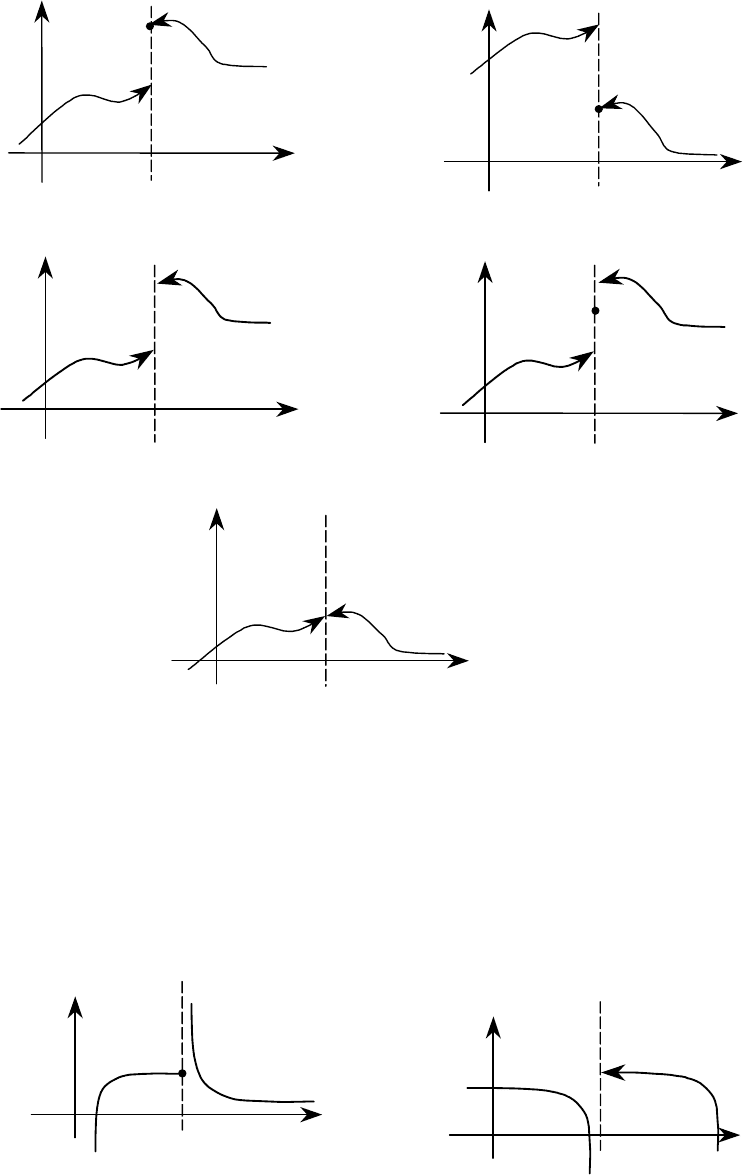
a
x
y
()
af
a
x
y
(
)
af
Рис. 15
a
x
y
(
)
af
a
y
()
af
x
Рис.16
a
x
y
(
)
существует не xf
(устранимый разрыв)
Рис. 17
Устранимый разрыв (для устранения разрыва положить
() () ()
xfxfaf
axax −→+→
== limlim
).
Точка разрыва а
называется точкой разрыва второго рода, если
()
±
∞=
+→
xf
ax
lim
и (или)
(
)
±
∞
=
−→
xf
ax
lim
(нарушается условие 2) непрерывности функции).
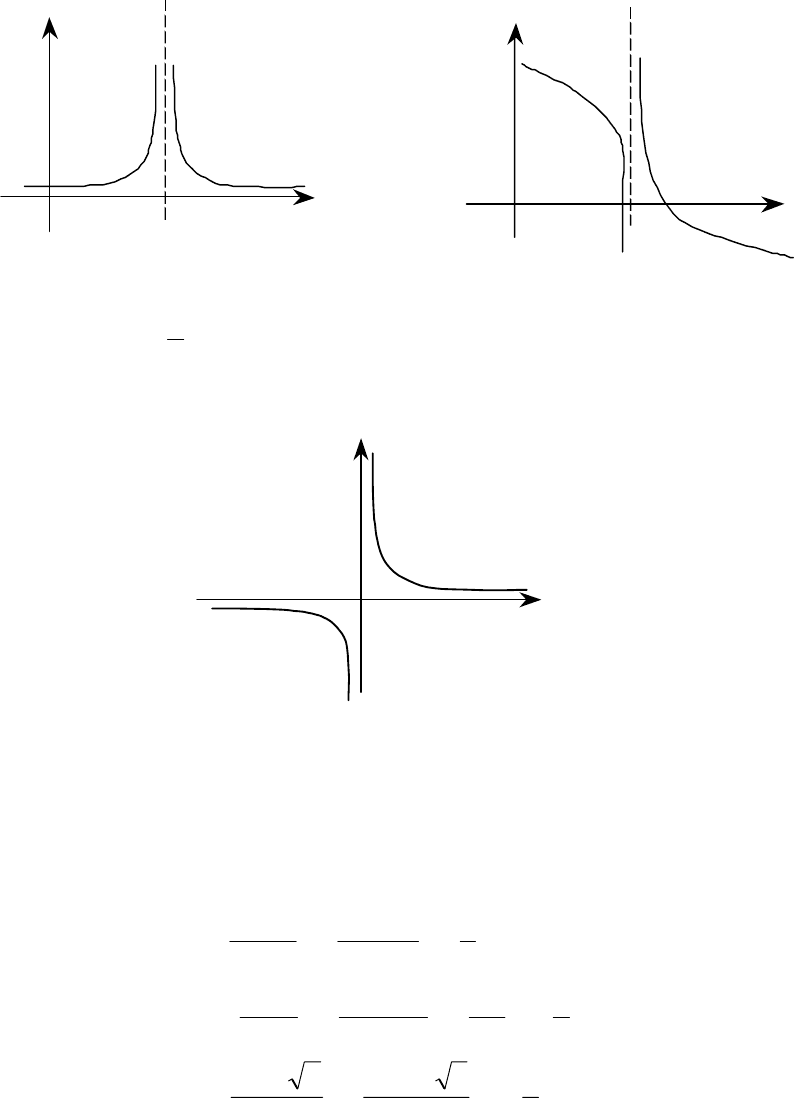
Графики функций с разрывами 2-го рода имеют вид
a
x
y
a
x
y
Рис. 18
x
y
a
x
y
Рис. 19
Пример.
x
y
1
= . Функция не определена при 0
=
x
. В этой точке она
имеет разрыв 2-го рода.
(
)
−
∞
=
−→
xf
x 0
lim
;
(
)
+
∞
=
+→
xf
x 0
lim
.
x
y
Разрыв 2-го рода
Рис. 20
§7. Вычисление пределов
Вычисление пределов начинается с подстановки вместо
x
числа, к ко-
торому стремится
x
(При
3→
x
, вместо
x
будем подставлять 3 и т.д.).
9
5
63
132
6
12
lim
3
=
⎟
⎠
⎞
⎜
⎝
⎛
+
−⋅
=
+
−
→
x
x
x
;
(
)
3
2
3
2
21
13
2
3
lim
1
−=
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−−
−+
=
−
+
−→
x
x
x
;
0
7
0
07
004
7
4
lim
0
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+⋅
=
+
+
→
x
xx
x
.
В этих пределах мы получили в результате числа, которые и дают ре-
зультат вычисления предела.
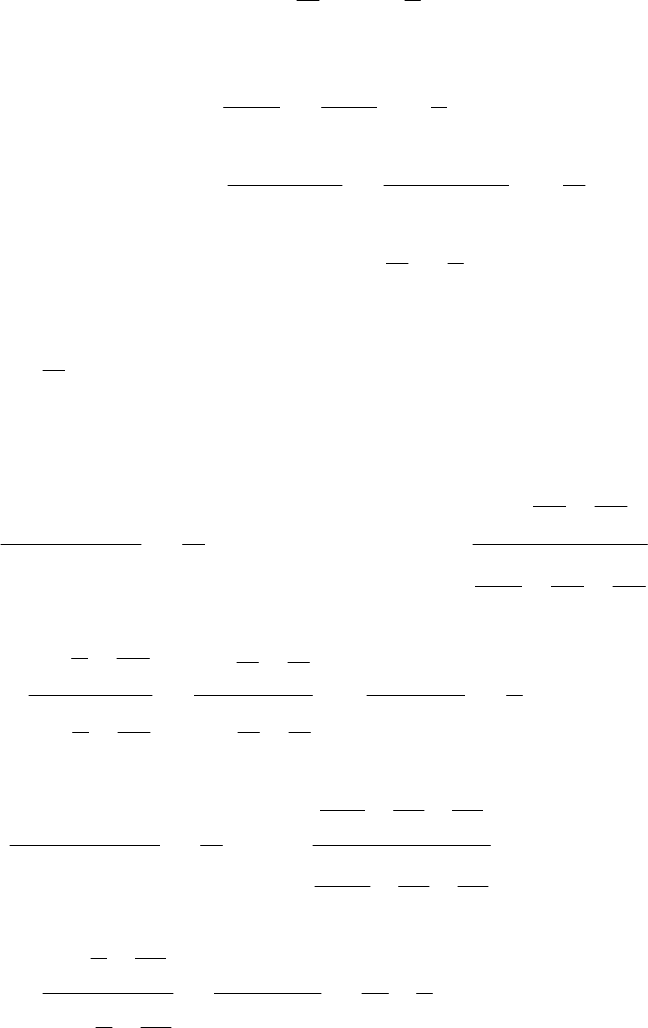
Необходимо помнить, что
.
0
1
;0
1
∞=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
∞
Например:
∞=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+
→
0
3
0
033
lim
0
x
x
x
;
0
2
3
2
3
2
lim
22
=
⎟
⎠
⎞
⎜
⎝
⎛
∞
=
⎟
⎠
⎞
⎜
⎝
⎛
−∞+∞
=
−+
∞→
xx
x
.
Ситуации, в которых получаем
(
)
(
)
0
0;1;
0
0
;
∞
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
∞
∞
считаются неопреде-
лённостями и вычисляются различными способами:
I)
⎟
⎠
⎞
⎜
⎝
⎛
∞
∞
Такая ситуация может возникнуть, например, при
∞→
x
при
делении многочлена на многочлен.
Нужно: разделить числитель и знаменатель на
x
в наибольшей степени.
а)
⎟
⎠
⎞
⎜
⎝
⎛
∞
∞
=
−+
−+
∞→
142
863
lim
2
2
x
x
xx
x
(делим на
2
x
) =
−+
−+
=
∞→
222
2
22
142
86
3
lim
x
x
x
x
x
xx
x
x
2
3
002
003
14
2
86
3
14
2
86
3
lim
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
−+
−+
=
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
∞
−
∞
+
∞
−
∞
+
=
−+
−+
=
∞→
x
x
x
x
x
.
б)
=
++
−+
=
⎟
⎠
⎞
⎜
⎝
⎛
∞
∞
=
++
−+
∞→∞→
222
2
222
2
2
2
316
2184
lim
316
2184
lim
x
x
x
x
x
xx
x
x
x
xx
xx
xx
4
1
16
4
0016
004
31
16
218
4
lim
2
2
==
⎟
⎠
⎞
⎜
⎝
⎛
++
−+
=
++
−+
=
∞→
x
x
x
x
x
;
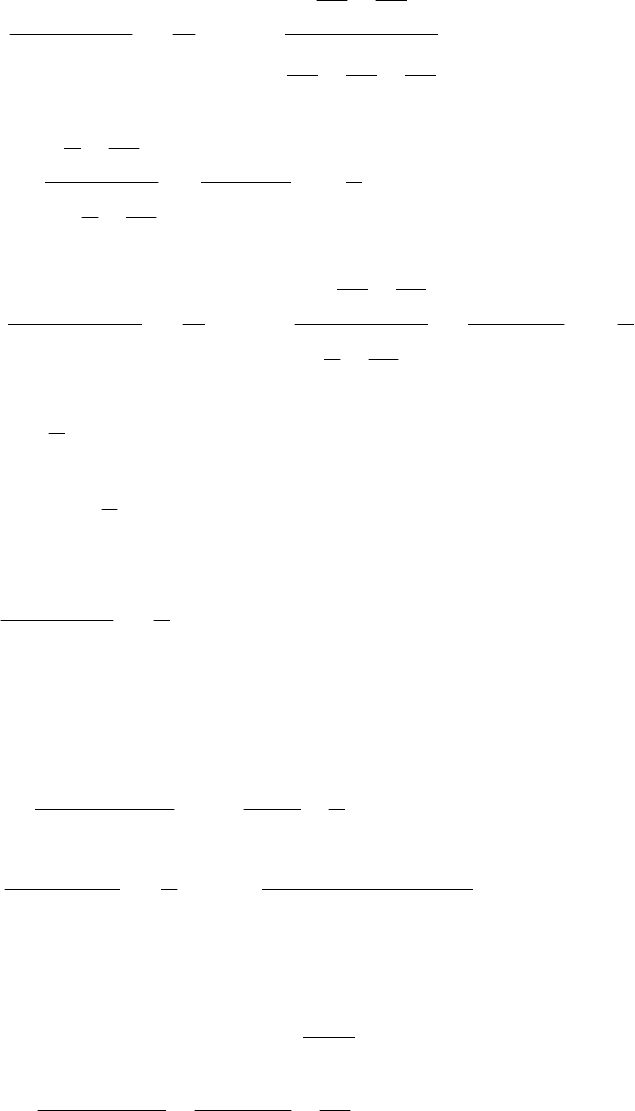
в)
=
+−
+
=
⎟
⎠
⎞
⎜
⎝
⎛
∞
∞
=
+−
+
∞→∞→
222
2
22
2
83
62
lim
83
62
lim
x
x
x
x
x
xx
x
xx
x
xx
0
1
0
001
0
83
1
62
lim
2
2
=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
+−
=
+−
+
=
∞→
x
x
x
x
x
;
г)
∞=
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
+
−+
=
+
−+
=
⎟
⎠
⎞
⎜
⎝
⎛
∞
∞
=
+
−+
∞→∞→
0
2
00
002
31
14
2
lim
3
142
lim
3
32
2
3
x
x
xx
x
xx
xx
.
II)
⎟
⎠
⎞
⎜
⎝
⎛
0
0
Если при
a
x
→
, при делении многочлена на многочлен получа-
ем ситуацию
⎟
⎠
⎞
⎜
⎝
⎛
0
0
, нужно числитель и знаменатель разложить на множители и
сократить одинаковые скобки.
а)
=
⎟
⎠
⎞
⎜
⎝
⎛
=
−+
−
→
0
0
2
1
lim
2
2
1
xx
x
x
(В числителе используем формулу разности квадратов, в знаменателе найдём
корни уравнения
02
2
=−+
x
x
;
1,2
2,1
−
=
x
поэтому знаменатель запишется в
виде
()( )()
(
)()
(
)
(
)
2121
21
+
−
=
−
−−=−− xxxxxxxx
)⇒
()()
()( )
3
2
2
1
lim
21
11
lim
11
=
+
+
=
+−
+−
=
→→
x
x
xx
xx
xx
;
б)
()
(
)
()()
=
+−
++−
=
⎟
⎠
⎞
⎜
⎝
⎛
=
−−
−
→→
23
933
lim
0
0
6
27
lim
2
3
2
3
3
xx
xxx
x
x
x
xx
(
06
2
=
−
−
x
x
;
(
)
256141
=
−
⋅
−
=D
;
,
2
51
2,1
±
=x
;3
1
=
x
2
2
−
=
x
.)
5
27
5
999
2
93
lim
2
3
=
++
=
+
++
=
→
x
xx
x
;
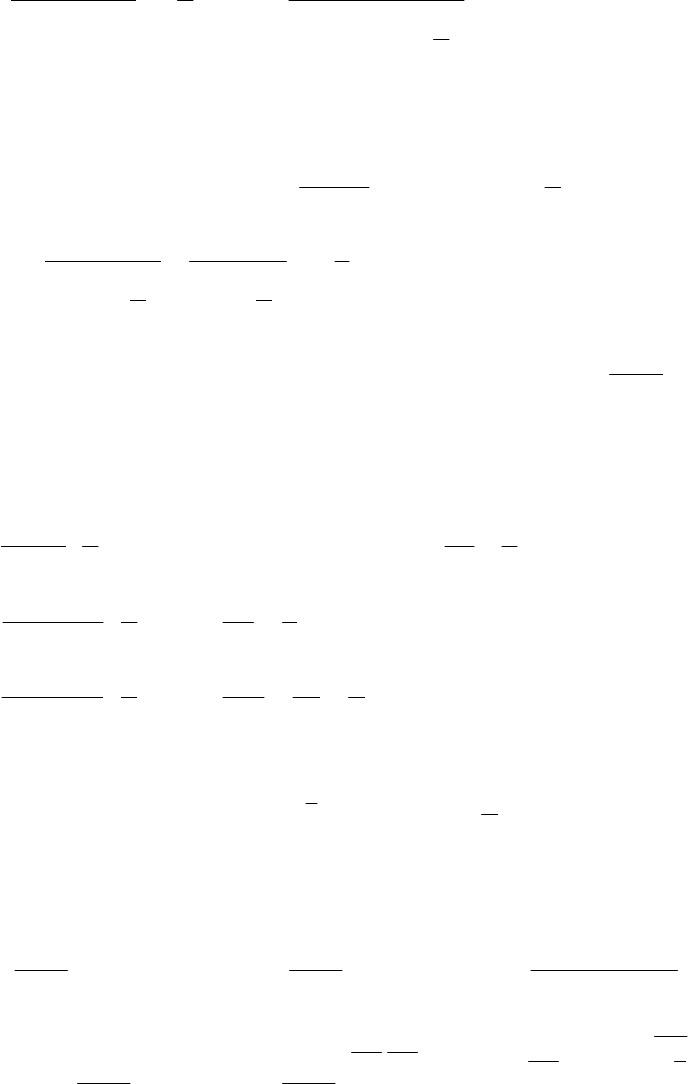
в)
()
=
⎟
⎠
⎞
⎜
⎝
⎛
−+
+
=
⎟
⎠
⎞
⎜
⎝
⎛
=
−+
+
−→−→
2
1
12
1
lim
0
0
12
1
lim
1
2
1
xx
x
xx
x
xx
(
012
2
=
−
+
x
x
;
(
)
92141
=
⋅
−
⋅
−
=D ;
4
31
2,1
±
−
=x
,
1
1
−
=
x ;
⎟
⎠
⎞
= .
2
1
2
x
3
1
6
3
2
1
2
1
2
1
lim
1
−=
⎟
⎠
⎞
⎜
⎝
⎛
−⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
−⋅
=
−→
x
x
.
III)
Первый замечательный предел имеет вид 1
sin
lim
0
=
→
x
x
x
отсюда по-
лучаем эквивалентности:
α
α
α
α
α
~
~
arcsi
n
~
~
sin arct
g
t
g
при 0→
α
.
Эквивалентные функции можно заменять друг на друга при вычисление пре-
делов
а)
()
5
3
5
3
lim5~5sin,3~3sin
0
0
5sin
3sin
lim
00
==
⎟
⎠
⎞
⎜
⎝
⎛
→→
x
x
xxxx
x
x
xx
;
б)
3
1
6
2
lim
0
0
6sin
2arcsin
lim
00
==
⎟
⎠
⎞
⎜
⎝
⎛
→→
x
x
x
x
xx
;
в)
3
2
12
8
12
8
lim
0
0
12
8
lim
00
===
⎟
⎠
⎞
⎜
⎝
⎛
→→
x
x
xarctg
xtg
xx
.
IV)
Второй замечательный предел
()
ex
x
x
=+
→
1
0
1lim
;
e
x
x
x
=
⎟
⎠
⎞
⎜
⎝
⎛
+
∞→
1
1lim
.
С помощью II замечательного предела вычисляются неопределённости
типа
(
)
∞
1
.
а)
()
(
)
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−−+
+=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
+==
⎟
⎠
⎞
⎜
⎝
⎛
−
+
∞→∞→
∞
∞→
x
x
x
x
x
x
x
xx
x
x
x
x
1
11
1lim1
1
1
1lim1
1
1
lim
2
1
1
2
1
2
1
2
2
1
limlim
1
2
1lim
1
2
1lim eee
xx
x
x
x
x
x
x
x
x
x
x
x
===
⎟
⎠
⎞
⎜
⎝
⎛
−
+=
⎟
⎠
⎞
⎜
⎝
⎛
−
+=
−
∞→
−
∞→
⋅
−
⋅
−
∞→∞→
;
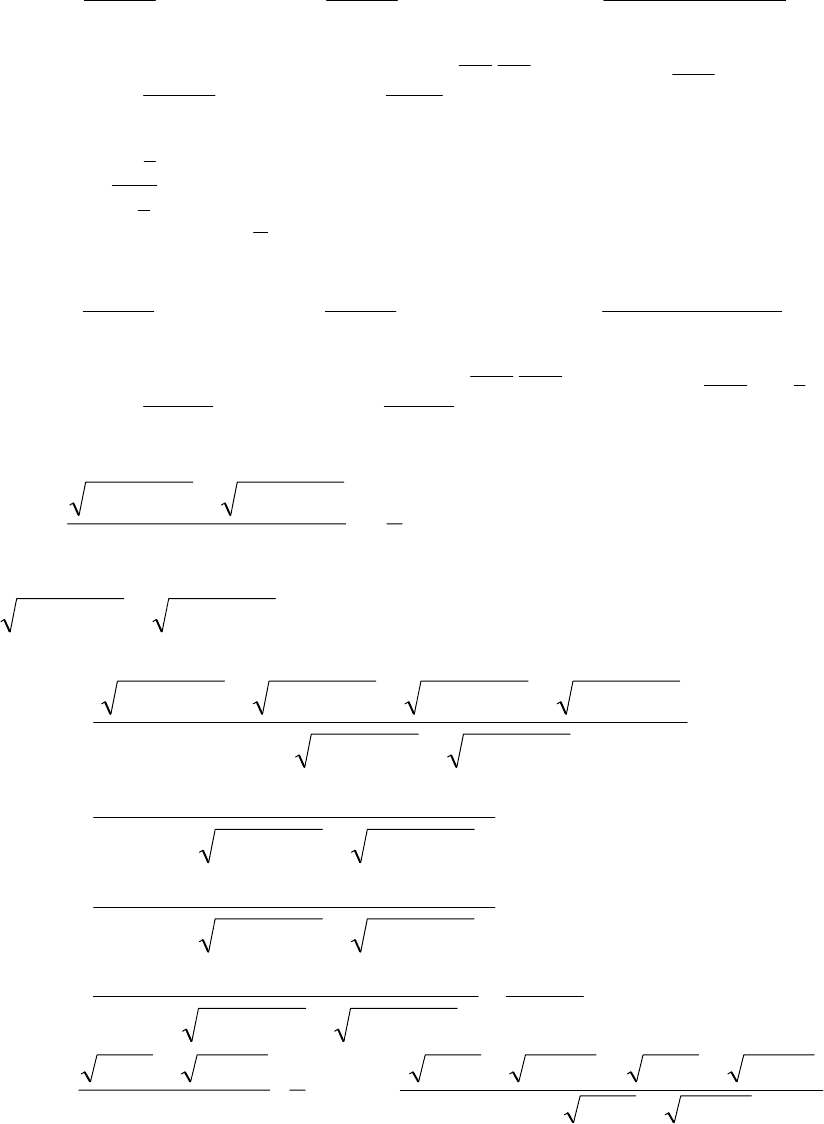
б)
()
=
⎟
⎠
⎞
⎜
⎝
⎛
+
+−+
+=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
+
+=
⎟
⎠
⎞
⎜
⎝
⎛
+
+
−
∞→
−
∞→
−
∞→
111
62
6242
1lim1
62
42
1lim
62
42
lim
x
x
x
x
x
x
x
xx
x
x
x
x
()
==
⎟
⎠
⎞
⎜
⎝
⎛
+
−
+=
⎟
⎠
⎞
⎜
⎝
⎛
+
−
+=
+
+−
∞→
−⋅
+
−
⋅
−
+
∞→
−
∞→
3
1
1
3
1
1
3
1
lim
3
1
1lim
62
2
1lim
x
x
x
x
x
x
x
x
x
e
xx
e
ee
x
x
x
1
lim
1
3
1
1
1
===
−
+
+−
∞→
.
в)
()
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−−+
+=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
+=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
+
∞→
+
∞→
+
∞→
111
36
3626
1lim1
36
26
1lim
36
26
lim
x
x
x
x
x
x
x
xx
x
x
x
x
()
6
5
36
55
1
36
5
5
36
1
lim
36
5
1lim
36
5
1lim ee
xx
x
x
x
x
x
x
x
x
x
==
⎟
⎠
⎞
⎜
⎝
⎛
−
+=
⎟
⎠
⎞
⎜
⎝
⎛
−
+=
−
+
∞→
+⋅
−
⋅
−
∞→
+
∞→
.
V)
Пределы различных функций
а)
=
⎟
⎠
⎞
⎜
⎝
⎛
=
−
+−−++
→
0
011
lim
2
22
0
xx
xxxx
x
Преобразуем функцию, домножив числитель и знаменатель дроби на скобку
(
)
22
11 xxxx +−+++
. В результате в числители получим выражение вида
()()
baba +⋅−
и используем формулу разности квадратов.
(
)
(
)
()
(
)
=
+−+++⋅−
+−+++⋅+−−++
=
→
222
2222
0
11
1111
lim
xxxxxx
xxxxxxxx
x
(
)
(
)
()
(
)
=
+−+++⋅−
+−⋅++
=
→
22
22
0
111
11
lim
xxxxxx
xxxx
x
()
(
)
=
+−+++⋅−
=
→
22
0
111
2
lim
xxxxxx
x
x
()
(
)
()
1
21
2
111
2
lim
22
0
−=
⋅−
=
+−+++⋅−
=
→
xxxxx
x
;
б)
(
)
(
)
()
()
=
+++⋅−
+++⋅+−+
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+−+
−→−→
6251
625625
lim
0
0
1
625
lim
2
1
2
1
xxx
xxxx
x
xx
xx
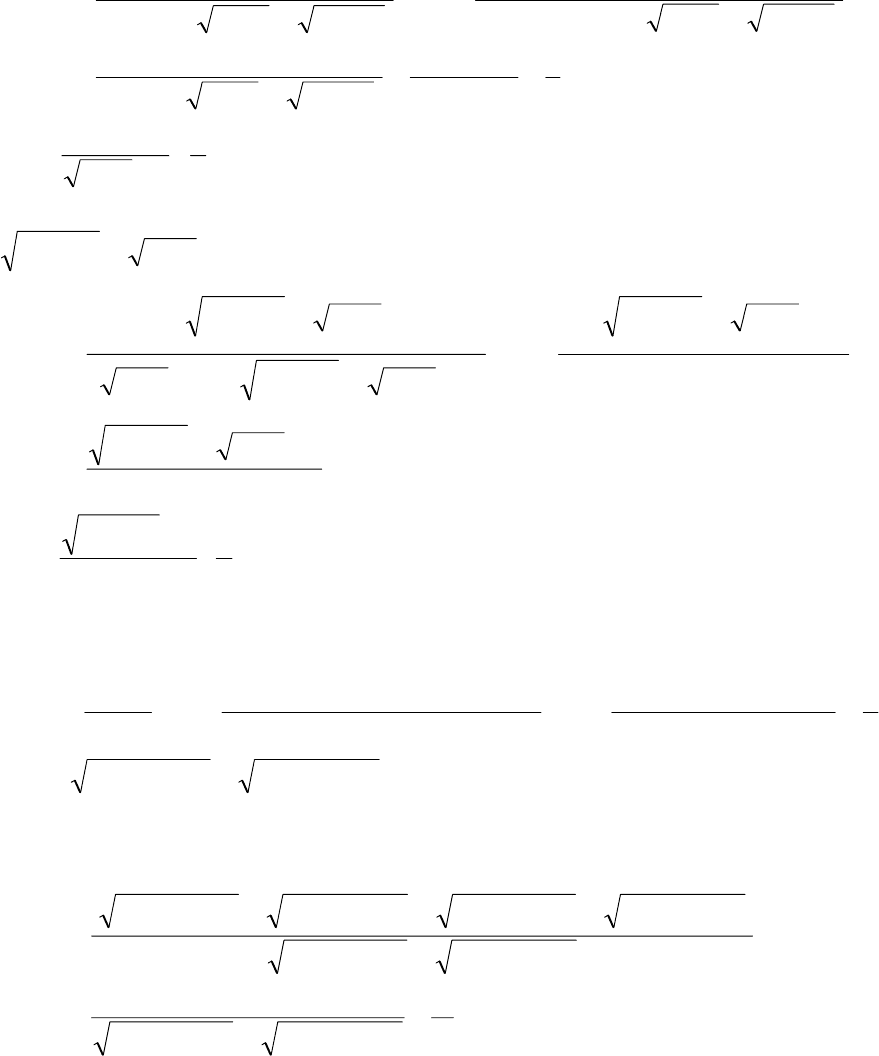
()( )
()
()
(
)
()()
()
=
+++⋅+⋅−
+
−
=
+++⋅−
+⋅+
=
−→−→
62511
1
lim
6251
625
lim
1
2
1
xxxx
x
xxx
xx
xx
()
()
()
8
1
222
1
6251
1
lim
1
=
+−
−
=
+++⋅−
−
=
−→
xxx
x
;
в)
=
⎟
⎠
⎞
⎜
⎝
⎛
−+
→
0
0
11
lim
3
0
x
x
x
Домножим знаменатель (и числитель) дроби на выражение
()
⎟
⎠
⎞
⎜
⎝
⎛
++++ 111
3
3
2
xx
, получим в знаменателе
(
)
(
)
111
32
−=++⋅− aaaa .
()
()
()
()
()
=
−+
⎟
⎠
⎞
⎜
⎝
⎛
++++⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
++++⋅−+
⎟
⎠
⎞
⎜
⎝
⎛
++++⋅
=
→→
11
111
lim
11111
111
lim
3
3
2
0
3
3
2
3
3
3
2
0
x
xxx
xxx
xxx
xx
()
3
1
111
lim
3
3
2
0
=
++++
=
→
xx
x
;
г)
()
=
⎟
⎠
⎞
⎜
⎝
⎛
−+
→
0
0
11
lim
5
3
0
x
x
x
Положим
5
1 yx =+
, тогда
1→y
при 0→
x
.
Значит
()
(
)
()
()
5
3
1
1
lim
11
11
lim
1
1
lim
234
2
1
234
2
1
5
3
1
=
++++
++
=
++++⋅−
++⋅−
=
−
−
=
→→→
yyyy
yy
yyyyy
yyy
y
y
yyy
;
д)
(
)
()
=∞−∞++−++
∞→
3438lim
22
xxxx
x
Домножим и разделим выражение на сумму корней и используем формулу
()()
22
bababa −=+⋅− .
(
)
(
)
=
+++++
+++++⋅++−++
=
∞→
3438
34383438
lim
22
2222
xxxx
xxxxxxxx
x
=
⎟
⎠
⎞
⎜
⎝
⎛
∞
∞
+++++
=
∞→
3438
4
lim
22
xxxx
x
x
Теперь разделим числитель и знаменатель дроби на
x
, получим
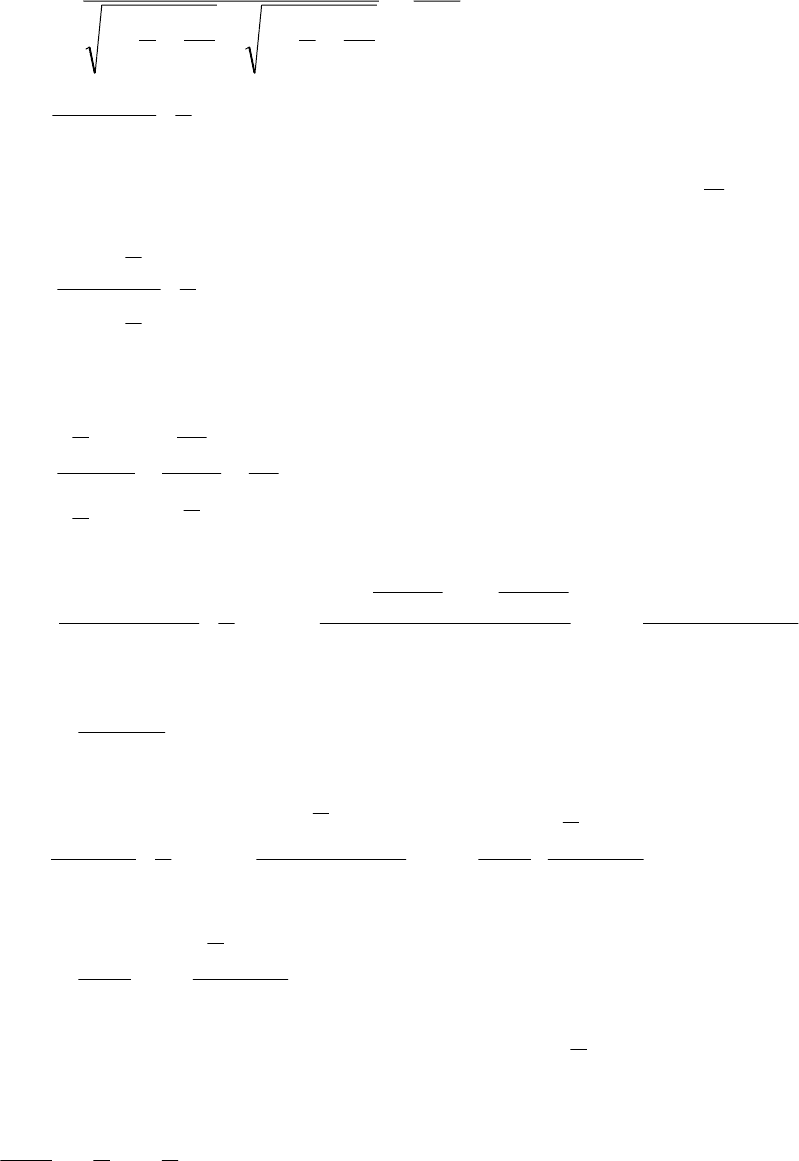
2
11
4
34
1
38
1
4
lim
22
=
+
=
+++++
=
∞→
x
x
x
x
x
;
е)
=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
→
0
0
3cos1
5cos1
lim
0
x
x
x
Преобразуем функцию, использовав формулу
2
sin2cos1
2
α
=α−
, получим
=
⎟
⎠
⎞
⎜
⎝
⎛
→
0
0
2
3
sin2
2
5
sin2
lim
2
2
0
x
x
x
Теперь заменим синусы на эквивалентные им функции
(
)
α
α
~sin
.
9
25
4
9
4
25
2
3
2
5
lim
2
2
0
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
→
x
x
x
;
ж)
() () ()
=
+
⋅
=
+
+
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
−
→→→
x
xx
x
xxxx
x
xx
xxx
1ln
2cossin2
lim
1ln
2
3
cos
2
3
sin2
lim
0
0
1ln
sin3sin
lim
000
Используем эквивалентность
α
α
~
sin
,
(
)
α
α
+
~1ln
при
0→
α
, получим
20cos2cos2lim
cos2
lim
00
====
→→
xx
x
xx
xx
;
з)
()
=
−
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
=
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
+
−
→→→
xxxx
xx
x
x
x
x
x
x
xx
x
1
4
5
1
4
lim
1
1
4
5
4
lim
0
045
lim
00
2
0
=
−
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
=
→→
xx
x
x
x
x
1
4
5
lim
1
4
lim
00
Второй предел является замечательным, равен
4
5
ln
(можно также использо-
вать эквивалентность
aa ln
~
1 α−
α
(при
0→
α
)).
4
5
ln
4
5
ln
10
4
0
=⋅
+
=
.

Контрольная работа №1 (часть 1)
I. Сделать линейные преобразования, найти определитель.
II. Решить систему методом Крамера;
III. Решить систему методом Гаусса.
IV. Решить матричное уравнение.
Вариант №1. Вариант №2.
I.
2188
6155
4321
1111−
;
II.
⎪
⎩
⎪
⎨
⎧
=−−
=−+
=+−
;376
;2
;153
zyx
zyx
zyx
III.
⎪
⎩
⎪
⎨
⎧
=−+
=+−
=
+−
;56
;123
;245
zyx
zyx
zyx
IV.
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
537
142
133
132
102
714
X .
I.
6423
7610
2116
5233
−−
;
II.
⎪
⎩
⎪
⎨
⎧
=+−
−=−+
=
+
−
;06
;14
;8432
zyx
zyx
zyx
III.
⎪
⎩
⎪
⎨
⎧
=++
=+−
=
−
+
;8426
;23
;7743
zyx
zyx
zyx
IV.
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
−
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
643
243
332
313
012
732
X .
Вариант №3. Вариант №4.
I.
8413
72224
81176
2233
−−
−
;
II.
⎪
⎩
⎪
⎨
⎧
=−+
=−−
=+−
;24846
;04
;043
zyx
zyx
zyx
III.
⎪
⎩
⎪
⎨
⎧
=+
−=−+
=
+−
;362
;16
;864
yx
zyx
zyx
I.
1256
0312
1341
1233
−
−
−
;
II.
⎪
⎩
⎪
⎨
⎧
=+−
=−−
−
=
+
+
;2643
;472
;533
zyx
zyx
zyx
III.
⎪
⎩
⎪
⎨
⎧
−=−−
=−+
=
−
−
;722
;243
;12
zyx
zyx
zyx

IV.
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
177
510
201
312
310
241
X . IV.
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
112
341
215
142
201
321
X .
Вариант №5. Вариант №6.
I.
2222
1116
4210
3115
−
−
;
II.
⎪
⎩
⎪
⎨
⎧
=−+−
=−+
=++
;352
;122
;233
zyx
zyx
zyx
III.
⎪
⎩
⎪
⎨
⎧
=−+
−=+−
=
+−
;35
;154
;234
zyx
zyx
zyx
IV.
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
511
232
010
015
654
123
X
I.
6113
4122
4452
2132
−
−−−
;
II.
⎪
⎩
⎪
⎨
⎧
−=++
=+−
=
−
+
;733
;276
;53
zyx
zyx
zyx
III.
⎪
⎩
⎪
⎨
⎧
=−+
=+−
=
+
−
;26
;8532
;114
zyx
zyx
zyx
IV.
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−
121
432
111
051
324
210
X .
Вариант №7. Вариант №8.
I.
12511
2111
1312
1312
−
−
−−
;
II.
⎪
⎩
⎪
⎨
⎧
=−+
=+−
=+−
;54
;43
;23
zyx
zyx
zyx
III.
⎪
⎩
⎪
⎨
⎧
−=−+
=+−
=
−+−
;273
;223
;15
zyx
zyx
zyx
I.
1111
2222
3333
1122
−−
−
−
;
II.
⎪
⎩
⎪
⎨
⎧
=++
=−−
=
+
−
;833
;13
;26
zyx
zyx
zyx
III.
⎪
⎩
⎪
⎨
⎧
=++
=−−
=
+
−
;833
;13
;26
zyx
zyx
zyx
