Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие
Подождите немного. Документ загружается.

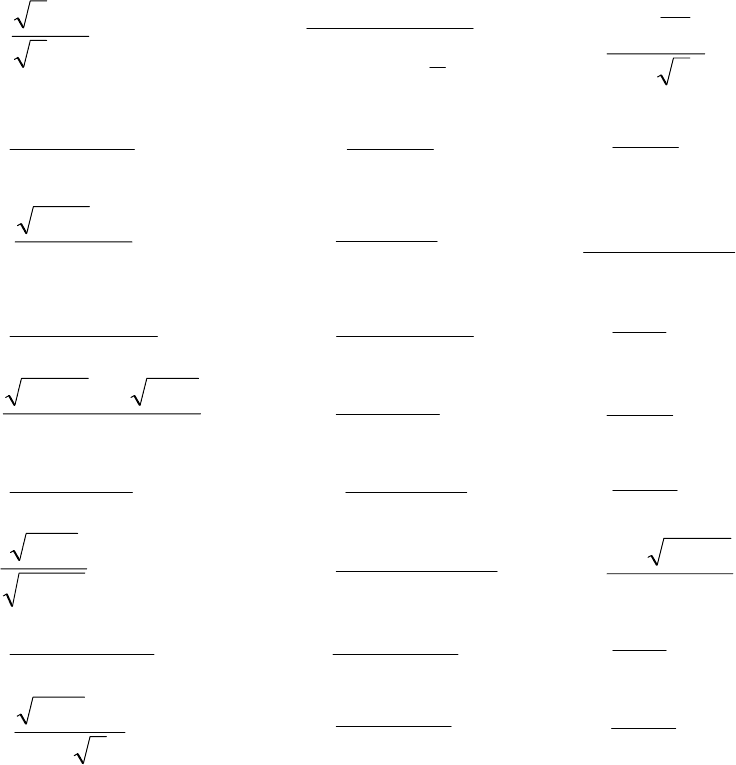
г)
4
2
lim
4
16
−
−
→
x
x
x
;
д)
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+π
→
2
1
2tg
2
lim
0
x
x
x
;
е)
x
x
x
−
⎟
⎠
⎞
⎜
⎝
⎛
π
→
1
2
cos
lim
1
;
27.
а)
36
84
lim
2
2
−
+
+−
∞→
x
x
xx
x
; б)
x
x
x
x
4
16
lim
2
2
4
+
−
−→
;
в)
x
x
x
4sin
8sin
lim
0→
;
г)
8
26
lim
3
3
2
+
+−
−→
x
x
x
;
д)
x
xx
x
3sin
53
lim
2
0
−
→
;
е)
x
xx
x
2tg
cos3cos
lim
2
−
π→
;
28.
а)
3128
17
lim
2
2
+
−
−+
∞→
x
x
xx
x
; б)
6
124
lim
2
2
2
−
+
−+
→
x
x
xx
x
;
в)
xtg
xtg
x
6
3
lim
0→
;
г)
9
1213
lim
2
3
−
+−+
→
x
xx
x
;
д)
2
3
0
4
cos1
lim
x
x
x
−
→
;
е)
x
x
x
π
−
→
sin
1
lim
2
1
;
29.
а)
83
8
lim
2
2
−
+
+−
∞→
x
x
xx
x
; б)
1
12
lim
2
2
1
−
+−
−→
x
xx
x
;
в)
x
x
x
5sin
8sin
lim
0→
;
г)
3
2
1
1
1
lim
−
−
→
x
x
x
;
д)
xx
x
x
3cos7cos
2cos1
lim
0
−
−
→
;
е)
x
x
x
π
−−
→
3sin
103
lim
1
;
30. а)
1816
874
lim
2
2
+−
++
∞→
x
x
xx
x
; б)
45
65
lim
2
2
1
+
−
−+
→
x
x
xx
x
;
в)
xtg
xtg
x
2
4
lim
0→
;
г)
3
8
2
31
lim
x
x
x
+
−−
−→
;
д)
1
10cos1
lim
2
0
−
−
→
x
x
e
x
;
е)
x
x
x
3tg
5sin
lim
π→
;
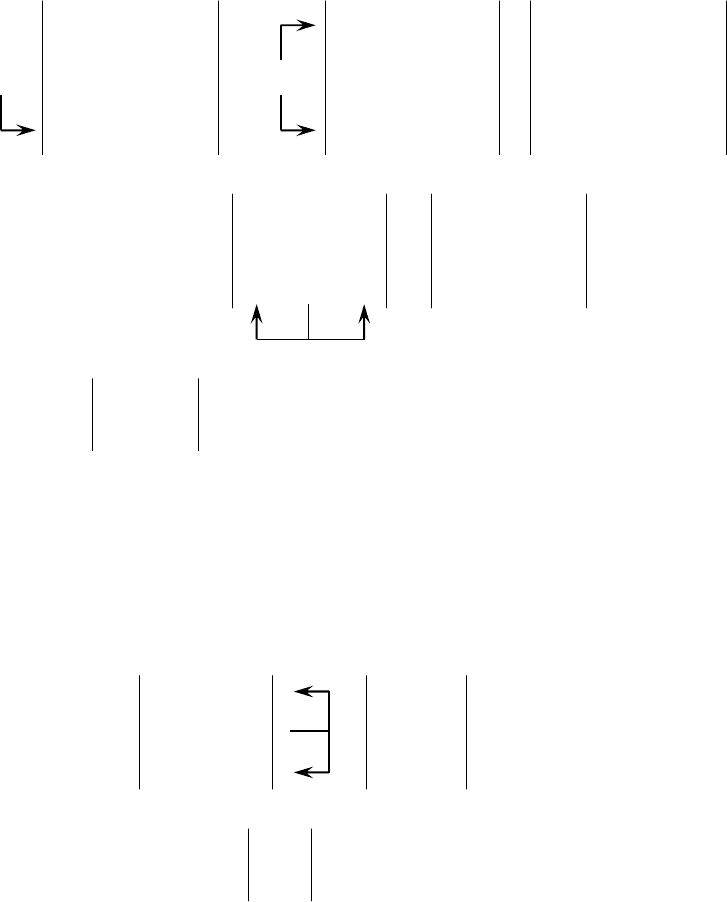
Раздел V. ПРИЛОЖЕНИЯ
Пример выполнения контрольной работы №1
Часть 1
I. Выполнить линейные преобразования, найти определитель:
() ()
=
−−−
−
−−
−
=
−
−
⋅−=
−
−
⋅−
5110
1110
3221
7130
1322
1110
3221
1312
2
1322
4131
3221
1312
1
Вычисляем определитель раскладывая по 1 столбцу
()
=
−−−
−
−
−
−
−=
−−
−
−
−
−
−⋅=
+
613
010
814
512
111
713
11
12
Делаем разложение по 2 строке
()() ()()()()()
618248364
63
84
11
22
=−=−⋅−−−⋅−+=
−−
−−
−⋅−−=
+
.
Ответ: 6.
II. Решим систему методом Крамера.
⎪
⎩
⎪
⎨
⎧
−=−−
=++
=
−
+
.13
;42
;03
zyx
zyx
zyx
Находим определитель системы:
113
112
131
det
−−
−
==∆
A
==
005
112
043
Делаем разложение по 3 строке
() ()
⇒≠=⋅−⋅⋅=⋅−⋅=
+
02001145
10
04
15
31
система крамеровская.
Ищем вспомогательные определители:
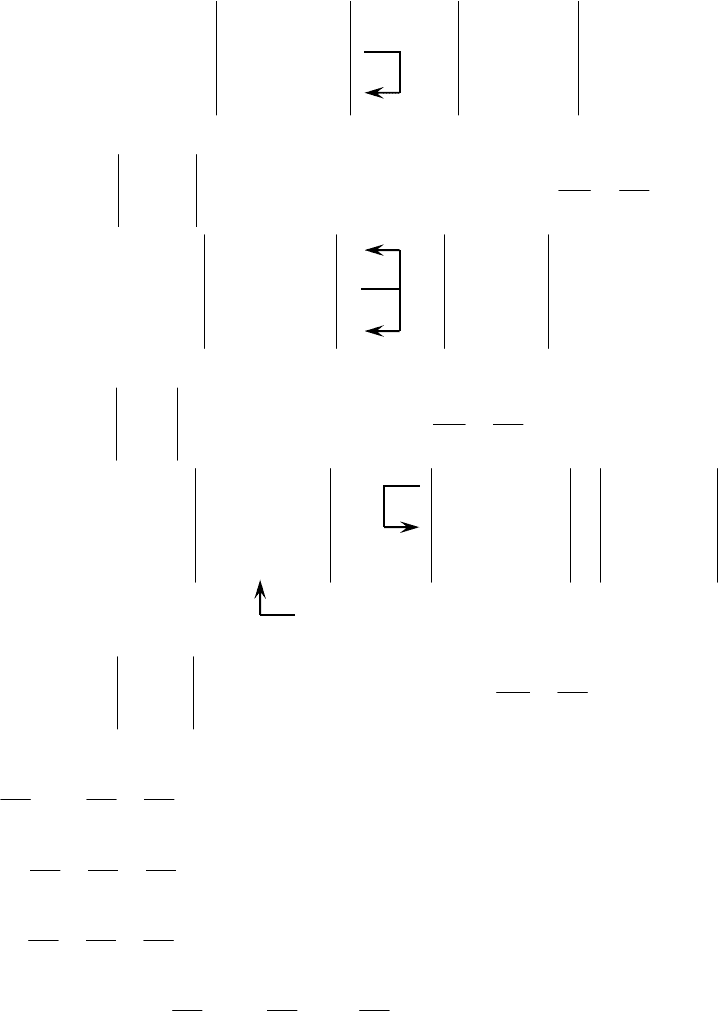
111
124
130
−−
−
=∆
x
=
−
=
004
113
130
Делаем разложение по 3 строке
() ()()
20
12
1243133
11
13
13
13
=
∆
∆
=⇒=⋅=−−⋅=
−
⋅−⋅=
+
x
x
.
113
112
131
−−
−
=∆
y
==
035
142
043
Делаем разложение по 3 столбцу
() ()
20
11
11209
35
43
11
32
=
∆
=⇒=−−=⋅−⋅=
+
y
y
y
.
=
−−
=∆
113
412
031
z
=
−
=
−
−
103
403
031
103
432
031
()
1−
Делаем разложение по 2 столбцу
() ()
20
45
451233
13
43
13
21
=
∆
∆
=⇒=−−⋅−=
−
⋅−⋅=
+
z
z
.
Проверка:
1) 0
20
45
20
11
3
20
12
=−⋅+ − верно;
2)
4
20
45
20
11
20
12
2 =++⋅
− верно;
3)
1
20
45
20
11
20
12
3 −=−−⋅ − верно.
Ответ:
.
20
45
;
20
11
;
20
12
=== zyx
III. Решим систему методом Гаусса.
⎪
⎩
⎪
⎨
⎧
−=−−
=++
=
−
+
.13
;42
;03
zyx
zyx
zyx
Выпишем матрицу системы и приведём её к треугольному виду:
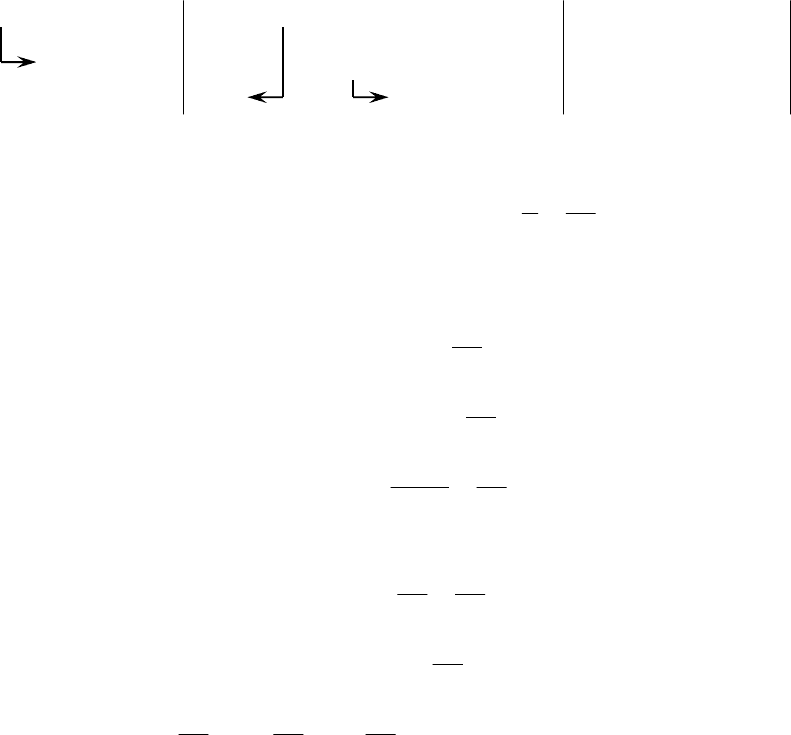
() ()
()
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
−
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
−
−
−
−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−−
−−
9
4
0
400
350
231
~
1
4
0
2100
350
131
2~
3
1
4
0
113
112
1312
Выписываем систему по получившейся матрице:
20
49
4
9
94
435
03
==⇒
⎪
⎭
⎪
⎬
⎫
−=⋅−
=⋅+⋅−
=
−
⋅+
z
z
zy
zyx
.
Подставляем
z во второе уравнение и находим y :
;4
20
45
35 =⋅+⋅− y
;
20
55
5 −=⋅− y
20
11
205
55
=
⋅
=y
.
Подставляем в первое уравнение
z
и
y
:
0
20
45
20
11
3 =−⋅+x
;
20
12
=
x .
Ответ:
.
20
45
;
20
11
;
20
12
=== zyx
IV. Решить матричное уравнение:
BA
X
⇓
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⇓
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
−
⋅
233
210
132
113
112
131
Решение. Уравнение можно записать в виде
;
B
A
X
=
⋅
()
;
11
−
−
⋅=⋅⋅ ABAAX
(
)
;
11
−
−
⋅=⋅⋅ ABAAX
;
1
−
⋅=⋅ ABEX
1−
⋅=
A
B
X
− формула для решения.
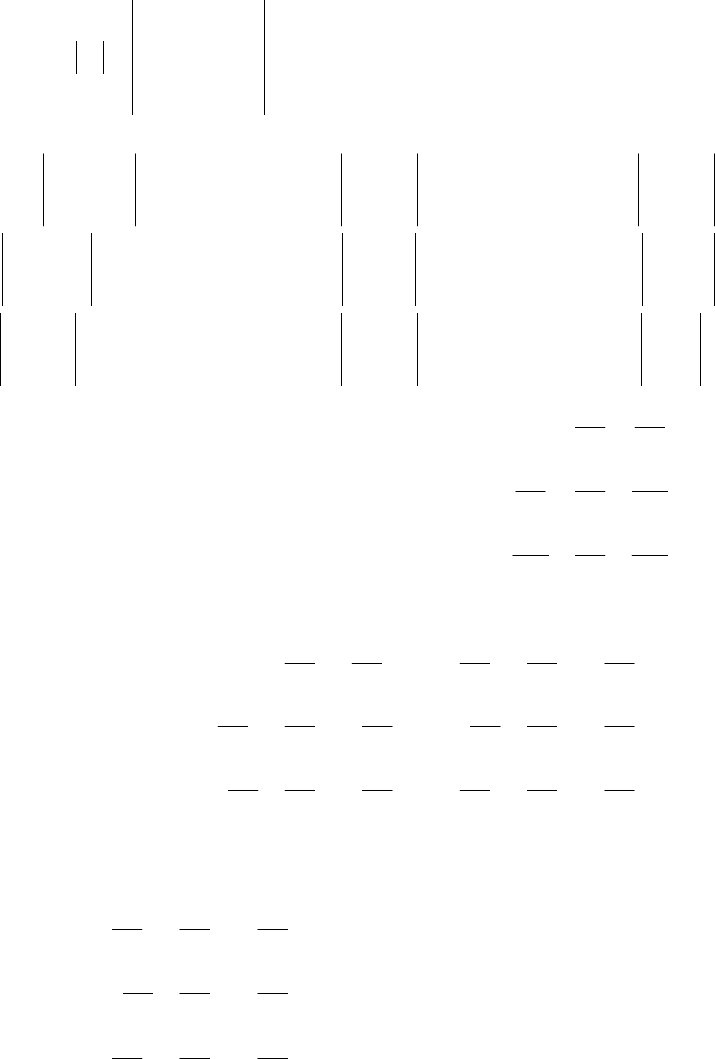
Найдём
1−
A
.
1
020
113
112
131
−
⇒≠=
−−
−
= AA существует.
Ищем алгебраические дополнения:
()
0
11
11
1
2
11
=
−−
−=A ; ;5
13
12
12
=
−
−=A ;5
13
12
13
−=
−
+=A
;4
11
13
21
=
−−
−
−=A ;2
13
11
22
=
−
−
+=A ;10
13
31
23
=
−
−=A
;4
11
13
31
=
−
+=A ;3
12
11
32
−=
−
−=A .5
12
31
33
−=+=A
Итак,
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
−
=
534
1024
550
~
A ;
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−−
−=
5105
325
440
~
T
A ;
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−−
−
=
−
20
5
20
10
20
5
20
3
20
2
20
5
20
4
20
4
0
1
A
.
Вычислим
X
:
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−−
−
=
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−−
−⋅
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
20
7
20
38
20
5
20
13
20
22
20
5
20
6
20
24
20
10
20
5
20
10
20
5
20
3
20
2
20
5
20
4
20
4
0
233
211
132
X
.
Теперь нужно подставить найденную матрицу
X в исходное уравнение, пере-
множить матрицы
X
A ⋅ , получить B (для проверки).
Ответ:
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−−
−
=
20
7
20
38
20
5
20
13
20
22
20
5
20
6
20
24
20
10
X
.
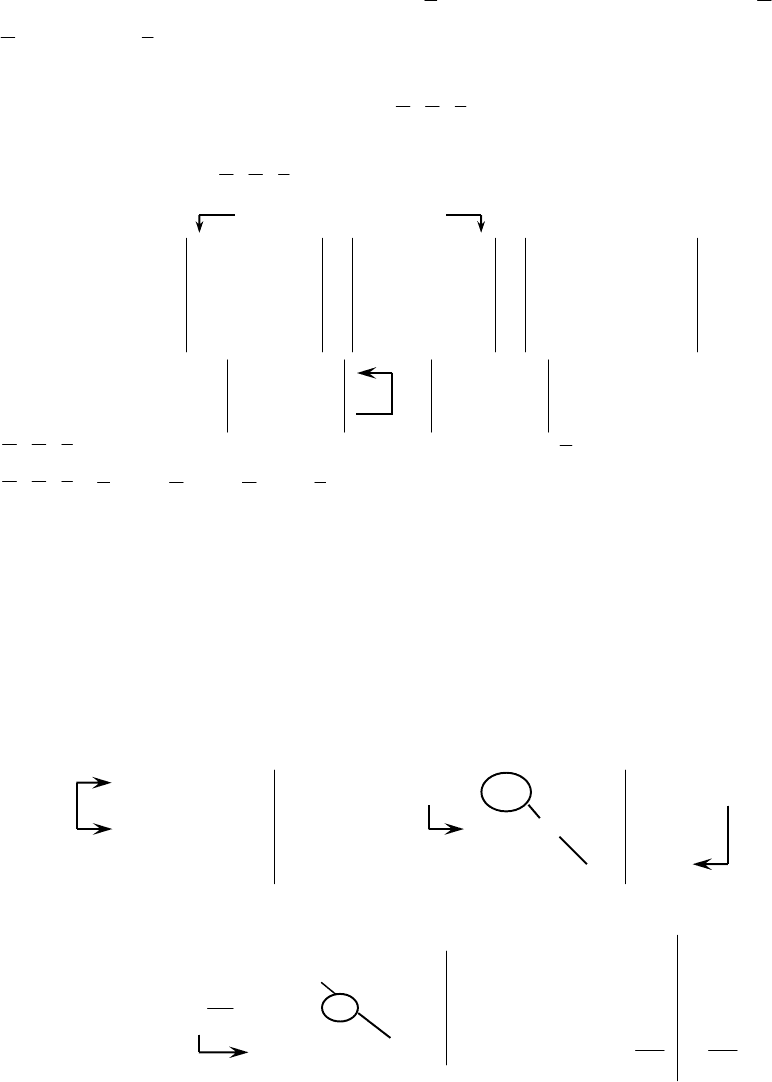
Часть 2
1. Написать разложение вектора
{
}
4,3,2
−
=
x по векторам
{}
,4,1,2 −=p
{}
,1,3,3=q
{}
0,3,2
−
=r
.
Решение
:
Проверим, образуют ли векторы
r
q
p
,,
базис в пространстве. Три вектора в
пространстве образуют базис, если они не компланарны. Составим определи-
тель из координат
r
q
p
,,
:
()
(
)
=
−−
−
=
−−
−
=
−
−
1234
1339
010
034
139
410
4
032
133
412
2
()()
124
139
11
3
−−
⋅−⋅−=
⇒≠−=+−=
−−
= 056460
124
15
r
qp ,, образуют базис. Следовательно, вектор
x
можно разложить по базису
r
q
p
,,
:
r
qp
x
⋅
γ
+⋅
β
+⋅δ=
.
Запишем равенство в координатах:
{}{}
{
}
{
}
0,3,21,3,34,1,24,3,2
−
⋅
γ
+
⋅
β
+
−
⋅δ=−
.
Приравниваем соответствующие координаты:
⎪
⎩
⎪
⎨
⎧
β+δ⋅=−
γ⋅−β⋅+δ−=
γ
⋅
+
β
⋅
+
δ
⋅
=
.44
;333
;2322
Решаем систему (любым методом) методом Гаусса:
(
)
(
)
~
4
4
2
3
014
232
3312
~
4
3
2
014
331
232 −
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−−−
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−
−−
.
9
32
8
3
9
56
00
490
331
~
8
8
3
12130
490
331
9
13
~
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
−−
−
−−
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
−
−−
⎟
⎠
⎞
⎜
⎝
⎛
−

Получили систему:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−=γ⋅−
=γ⋅−β⋅
=γ⋅−β⋅+δ−
.
9
32
9
56
;849
;333
Решаем: из третьего уравнения
;
7
4
56
32
==γ
Подставим
γ
во второе уравнение:
;8
7
16
9
=−β⋅
;
7
72
7
16
7
56
9 =+=β⋅
7
8
=β
;
Теперь из первого уравнения:
3
7
12
7
24
=−+δ− ;
7
9
7
12
7
21
=−=δ− ;
7
9
−=δ .
Проверка:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
−=−=+−
==−+
==++−
;4
7
28
7
8
7
36
;3
7
21
7
12
7
24
7
9
;2
7
14
7
8
7
24
7
18
− верно.
Ответ: rqpx
7
4
7
8
7
9
+⋅+⋅−= − разложение
x
по базису
r
q
p
,,
.
2. Коллинеарны ли векторы
1
c
и
2
c
, построенные по векторам
a
и
b
?
{
}
;1,3,2=a
{
}
.2,0,4=b
;3
1
bac −⋅=
.32
2
bac ⋅+⋅=
Решение:
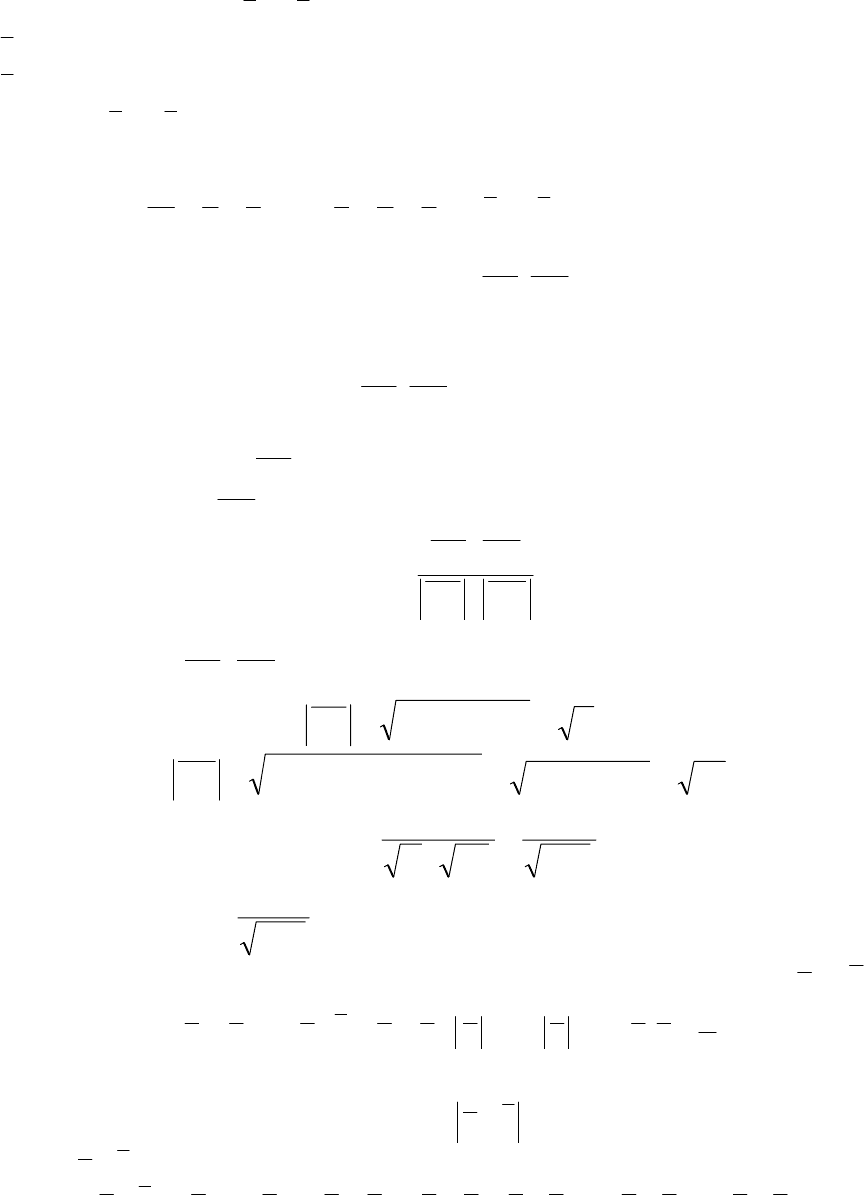
Найдём координаты
1
c
и
2
c
:
{}{ }{}
{
}
{
}
1,9,22,0,43,9,62,0,41,3,23
1
=
−
=−⋅=c ;
{}
{
}{ }
{
}
{
}
8,6,166,0,122,6,42,0,431,3,22
2
=
+
=⋅+⋅=c .
Векторы
1
c
и
2
c
коллинеарны, если их координаты пропорциональны. Соста-
вим пропорции:
;
8
1
6
9
16
2
== или ⇒≠≠
8
1
2
3
8
1
1
c
и
2
c
не коллинеарны.
Ответ: не колинеарны.
3. Найти косинус угла между векторами:
ACAB,
.
()
(
)
(
)
0,3,2;4,1,3;3,1,2
−
− CBA .
Решение:
Найдём координаты векторов
ACAB,
. Для этого из координат конца нужно
вычесть координаты начала.
(
){}
{
}
1;2;134;11;23 =−−−−=AB
;
(
){}
{
}
3;4;430;13;22 −−=−−−−−=AC
.
Теперь используем формулу
ACAB
ACAB
⋅
⋅
=δcos
.
Считаем:
()
(
)
1384314241 =−+−=−⋅+⋅+−⋅=⋅ ACAB ;
6121
222
=++=AB ;
() ()
4191616344
2
2
2
=++=−++−=AC
;
246
1
416
1
cos
=
⋅
=δ .
Ответ:
246
1
cos =δ
.
4. Вычислить площадь параллелограмма, построенного на векторах
a
и b
6
,;3;2;;3
π
===−=⋅+=
∧
qpqpqpbqpa .
Решение:
baS ×=
.пар
.
Ищем
ba × :
()()
=×⋅−×⋅+×−×=−×⋅+=× qqqpqpppqpqpba 333
(используем то, что pqqpqqpp
×
−
=
×
=
×
=× ;0;0 )
p
q
p
q
p
q
×
⋅
=
×
⋅
+
×= 43
.
Далее:
=⋅⋅⋅=×⋅=×
∧
qpqpqpba ,sin44
r
12
2
1
324
6
sin324 =⋅⋅⋅=
π
⋅⋅⋅= .
Ответ: площадь равна 12 квадратных единиц.
5. Компланарны ли векторы
cba ,,
?
{}
{
}
{
}
3,1,0;4,1,3;1,3,2 cba − .
Решение:
Векторы компланарны, если их смешанное произведение рано нулю. Сме-
шанное произведение ищем через определитель:
⇒≠−=−−−++−=−=⋅⋅ 0388270306
310
413
132
cba
некомпланарны.
Ответ: некомпланарны.
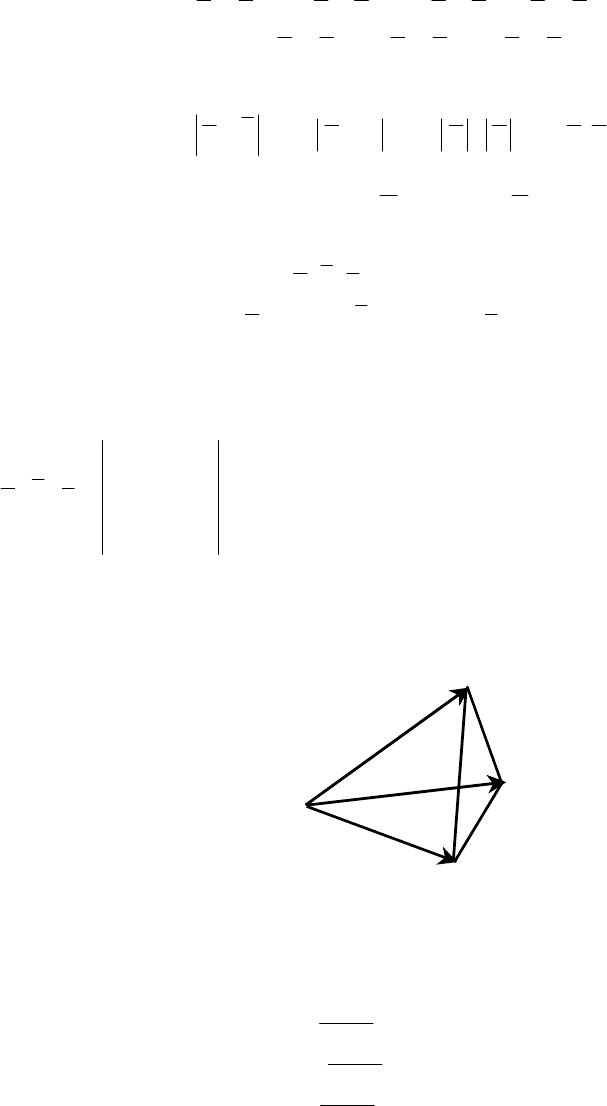
6. Вычислить объём тетраэдра с вершинами в точках
4321
,,, AAAA и его вы-
соту, опущенную на грань
321
,, AAA .
A
1
A
3
A
2
A
4
Рис. 1
()( )()
(
)
.2,2,2;4,1,2;1,1,3;2,1,0
4321
−
− AAAA
Решение:
Ищем координаты векторов:
{
}
;3,0,3
21
−=AA
{
}
;2,0,2
21
=AA
{
}
.0,3,2
21
−=AA
()
()
3
413121
ед6
6
36
1818
6
1
031
202
303
6
1
6
1
==+⋅=
−
−
⋅=⋅⋅⋅=
∆
AAAAAAV
.
С другой стороны,
HSV
осн
⋅⋅=
∆
3
1
(*)
Найдём:
=⋅⋅==
∆ 3121.
2
1
321
AAAASS
AAAосн
=⋅+
−
⋅−
−
⋅⋅=−⋅=
02
03
22
33
20
30
2
1
202
303
2
1
kji
kji
()
()
22
2
2
ед612
2
1
0120
2
1
0120
2
1
=⋅=+−+⋅=⋅+⋅−⋅⋅= kji
.
Подставляем в формулу (*):
;6
3
1
6 H⋅⋅=
(
)
ед3
=
H .
Ответ:
(
)
;ед6
3
=V
(
)
ед3=H .
Часть 3
1. Найти расстояние от точки
(
)
1;3;2
0
−
M
до плоскости, проходящей через
три точки
()()
(
)
0;1;2,4;3;2,1;1;1
321
MMM −
.
Решение:
Составим уравнение плоскости, проходящей через три точки
321
,, MMM :
(
)
()
()
;0
101112
141213
111
=
−−−−
−−−−
−
−
−
− zyx
или
