Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие
Подождите немного. Документ загружается.

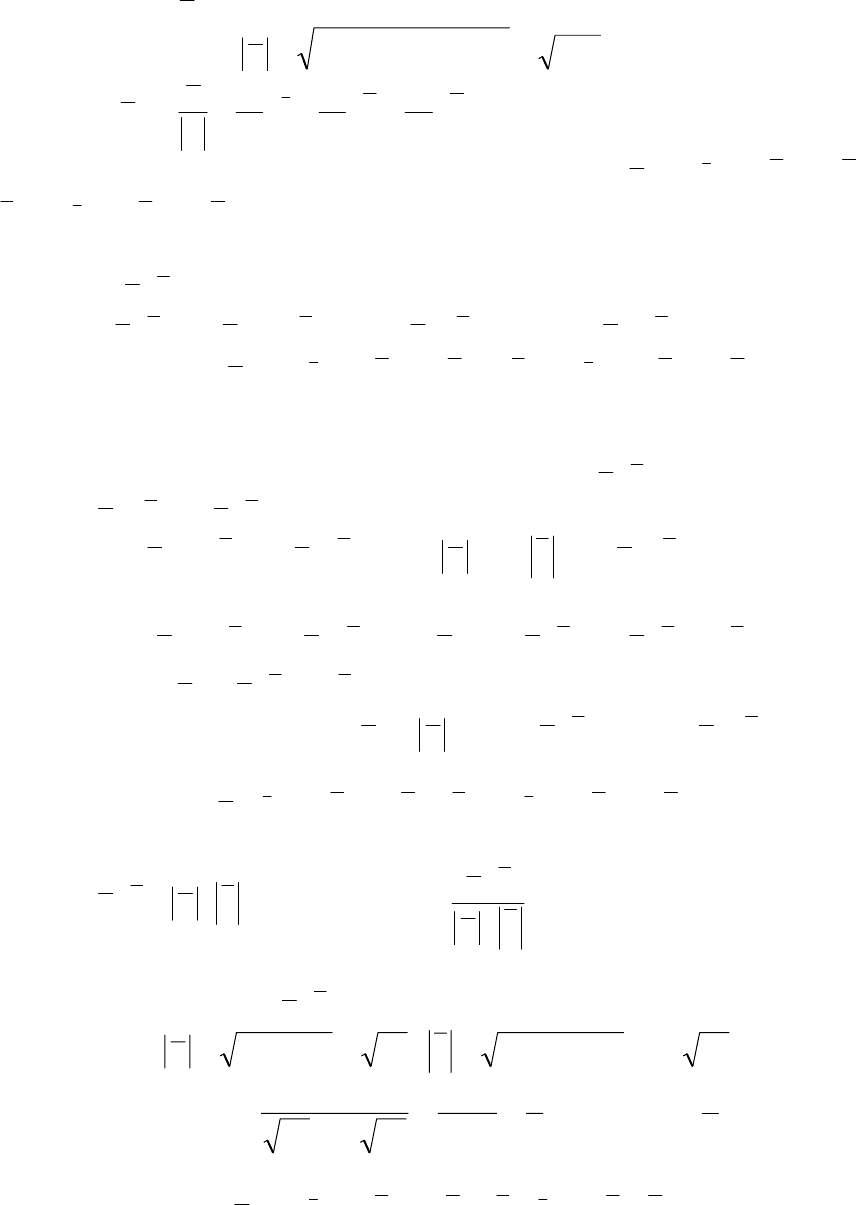
Найдём длину
a
:
()
131691243
2
22
==−++=a .
Поэтому:
kji
a
a
a
o
⋅−⋅+⋅==
13
12
13
4
13
3
.
5. Найти скалярное произведение векторов kjia ⋅+⋅+⋅= 743 и
kjib ⋅+⋅−⋅= 252.
Решение:
Находим
()
0275423 =⋅+−⋅+⋅=⋅ ba . Так как скалярное произведение
векторов
0;0;0 ≠≠=⋅ baba , то ba
⊥
. Векторы
a
и b ортогональны.
6. Даны векторы kjima ⋅+⋅+⋅= 43 и kjmib ⋅−⋅+⋅= 74. При каком
значении m эти векторы перпендикулярны?
Решение:
Находим скалярное произведение этих векторов .03834
=
−⋅+
⋅
=
⋅
mmba
Так как
ba ⊥ , то 0=⋅ ba . Отсюда 0287
=
−
⋅
m , 4
=
m .
7. Найти
(
)
(
)
baba −⋅⋅⋅+⋅ 235, если ,3,2 == ba ba
⊥
.
Решение:
()()
=⋅−⋅⋅+⋅⋅−⋅=−⋅⋅⋅+⋅
2
2
36510235 bbabaababa
132740330210310
22
2
2
=
−
=
⋅
−
+
⋅
=
⋅−⋅
+
⋅= bbaa ;
Здесь использованы свойства
;2
2
2
2
== aa
0
=
⋅
ba , при ba ⊥ .
8. Определить угол между векторами
kjia ⋅+⋅+= 32 и .246 kjib ⋅−⋅+⋅=
Решение:
Так как
ϕ⋅⋅=⋅ cosbaba
, то
ba
ba
⋅
⋅
=ϕcos .
Имеем
(
)
;8234261 =−⋅+⋅+⋅=⋅ ba
;14241636;14941 ⋅=++==++= ba
7
2
142
8
14214
8
cos =
⋅
=
⋅⋅
=
ϕ
и
7
2
arccos=
ϕ
.
9. Найти векторное произведение векторов
kjia ⋅+⋅+⋅= 532 и .2 kjib +⋅+=
Решение:
Имеем:
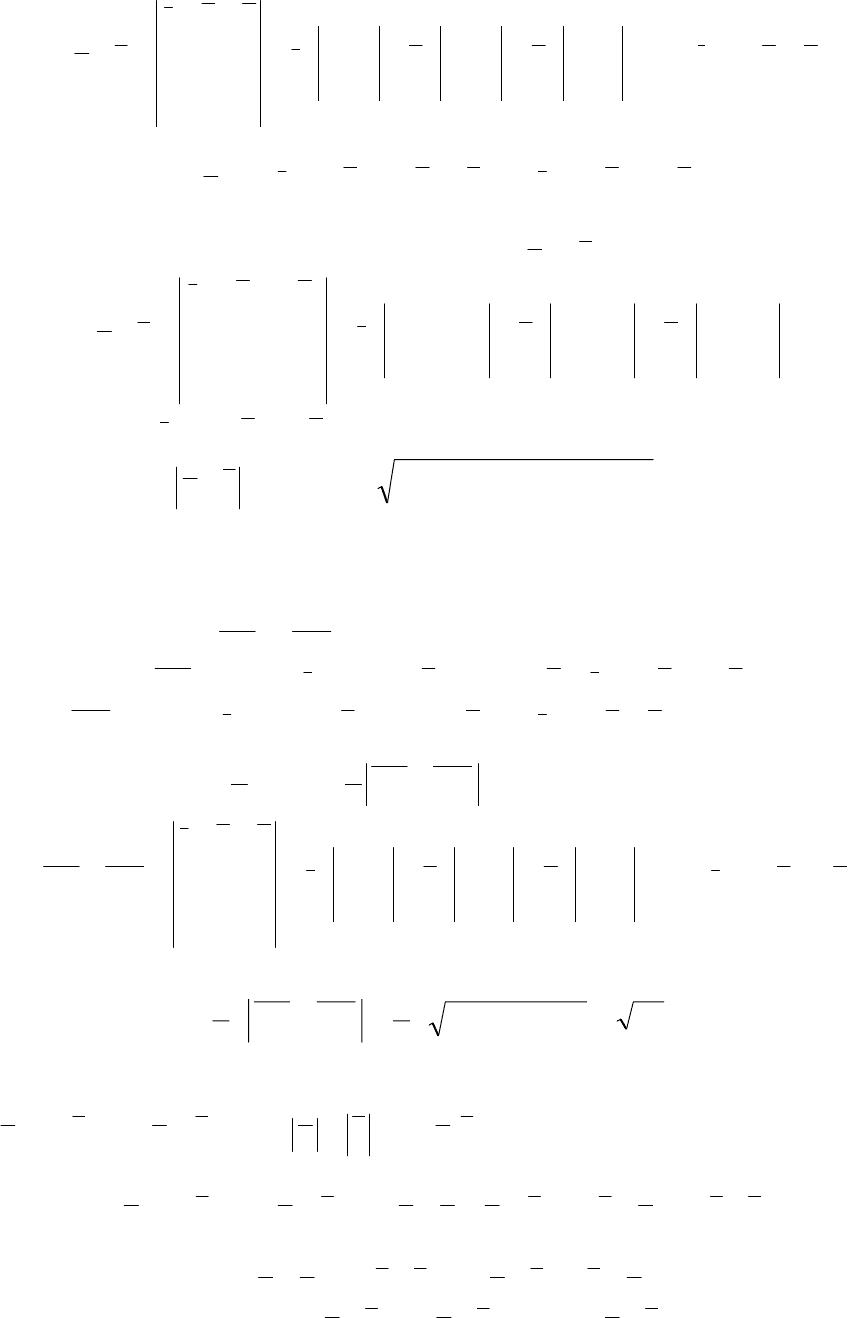
kjikji
kji
ba −⋅+⋅−=⋅+⋅−⋅==× 37
11
32
11
52
12
53
121
532.
10. Вычислить площадь параллелограмма, построенного на векторах
kjia ⋅−⋅+⋅= 236 и .623 kjib ⋅+⋅−⋅=
Решение:
Находим векторное произведение векторов
a
и b :
.214214
23
36
63
26
62
23
623
236
kji
kji
kji
ba
−⋅−⋅=
=
−
⋅+
−
⋅−
−
−
⋅=
−
−=×
Так как
baS ×=
.пар
, то
()() ()
кв.ед49214214
22
2
.пар
=−+−+=S
.
11. Вычислить площадь треугольника с вершинами
(
)
1,1,1A ;
()
4,3,2B ;
()
2,3,4C .
Решение:
Находим векторы
A
B и
A
C :
(
) ()
(
)
kjikjiAB ⋅+⋅+=⋅−+⋅−+⋅−= 32141312
()()
(
)
kjikjiAC +⋅+⋅=⋅−+⋅−+⋅−= 23121314.
Известно, что
ACABSS ×=⋅=
∆
2
1
2
1
.пар
. Найдём:
kjikji
kji
ACAB 484
23
21
13
31
12
32
123
321 −⋅+⋅−=⋅+⋅−⋅==× .
Следовательно,
()
кв.ед.24166416
2
1
2
1
=++⋅=×⋅=
∆
ACABS
12. Вычислить площадь параллелограмма построенного на векторах
ba ⋅+ 3 и ba +⋅3, если
()
o
30,,1 ===
∧
baba .
Решение:
(
)
(
)
=×⋅+×⋅+++×⋅=+⋅×⋅+ bbabbaaababa 39333
используем свойства векторного произведения:
;0=× aa ;0=× bb abba
×
−
=
×
bababa
×
−
=
⋅
+
×
⋅
−
×+⋅= 03903.
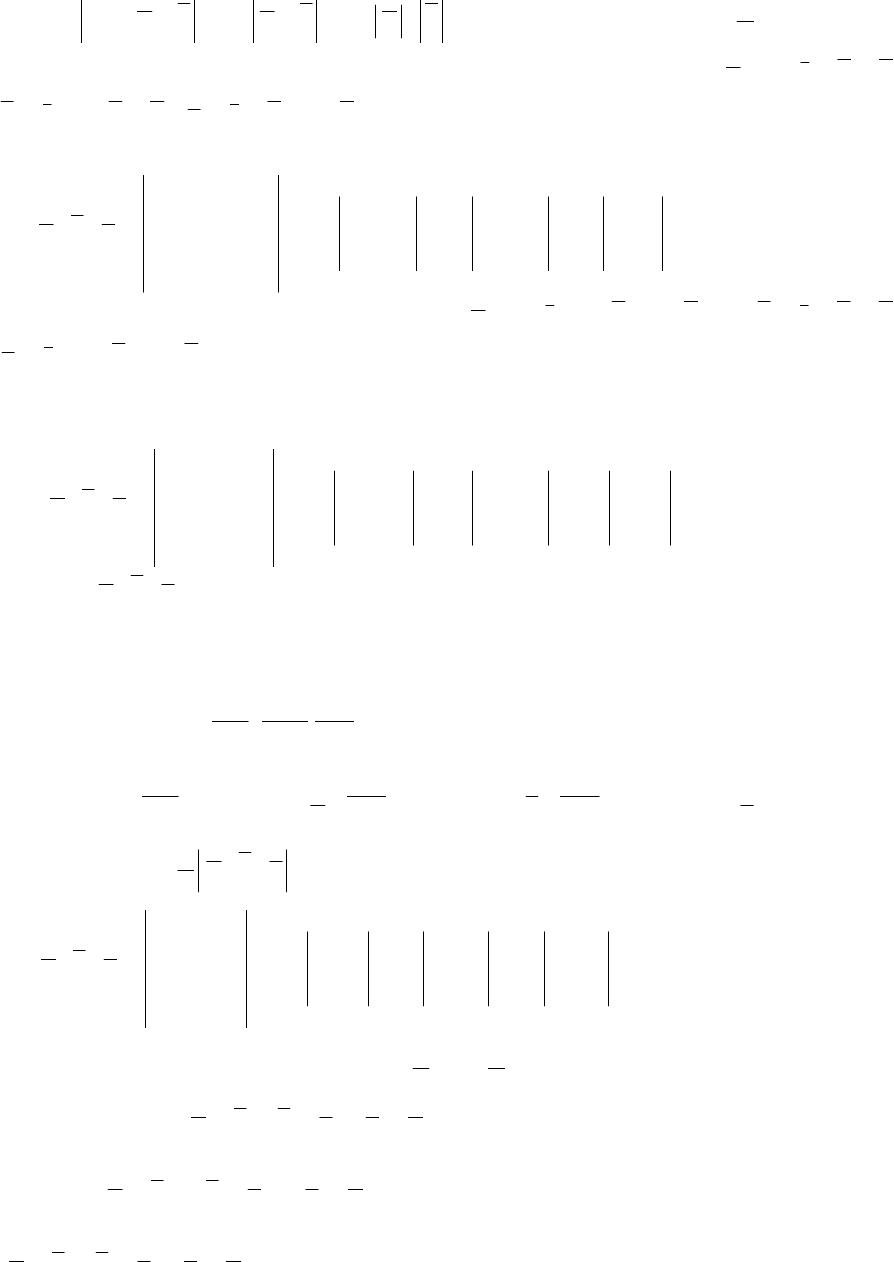
Далее:
()
кв.ед.4
2
1
830sin118sin888
.пар
=⋅=⋅⋅⋅=ϕ⋅⋅=×⋅=×⋅−=
o
bababaS .
13. Найти смешанное произведение векторов: kjia −−⋅= 2,
kjib −⋅+= 3, kjiс ⋅++= 4.
Решение:
332526
11
31
1
41
11
1
41
13
2
411
131
112
=++=⋅−
−
⋅+
−
⋅=−
−−
=⋅⋅ cba .
14. Показать, что векторы kjia ⋅+⋅+⋅= 752, ,kjib −+=
kjiс ⋅+⋅+= 22 компланарны.
Решение:
Находим смешанное произведение векторов:
07158
21
11
7
21
11
5
22
11
2
221
111
752
=+−=⋅+
−
⋅−
−
⋅=−=⋅⋅ cba .
Так как
0=⋅⋅ cba , то векторы компланарны.
15. Найти объём треугольной пирамиды с вершинами
(
)
2,2,2A ;
()
3,3,4B ;
()
4,5,4C ;
()
6,5,5D .
Решение:
Найдём векторы ADACAB ,, , совпадающие с ребрами пирамид (все век-
торы должны исходить из одной точки).
{
}
;1,1,2 aAB ==
{
}
;2,3,2 bAC ==
{
}
.4,3,3 cAD ==
Так как
cbaV ⋅⋅=
6
1
.пир
, найдём смешанное произведение
7312162
33
32
1
43
22
1
43
23
2
433
232
112
=⋅−⋅−⋅=⋅+⋅−⋅==⋅⋅ cba .
(
)
3
.пир
ед
6
7
7
6
1
=⋅=V .
16. Вычислить
(
)
(
)
(
)
accbba −⋅−⋅− .
Решение:
Так как
(
)
(
)
()
0=−+−+− accbba
, то эти векторы компланарны. Следова-
тельно, их смешанное произведение равно нулю:
(
)
(
)
()
0=−⋅−⋅− accbba .
Задачи для самостоятельного решения
1. Даны координаты вершин треугольника
(
)( )( )
1,4,1;1,2,3;3,2,1 CBA .
Показать, что треугольник равносторонний.
2. Вычислить модуль вектора
(
)
kjikjia ⋅+⋅+⋅⋅−+⋅+= 384
5
1
2 и найти
его направляющие косинусы.
3. Даны точки
(
)
3,2,1
1
M и
(
)
6,4,3
2
−
M . Найти длину и направление век-
тора
2
1
MM
.
4. Дан вектор kjia ⋅+⋅−⋅= 324. Найти вектор b , если ab = , первая
координата
b равна 0, вторая координата b равна второй координате a .
5. Радиус-вектор точки
M
составляет с осью Oy угол 60 градусов, а с
осью Oz угол 45 градусов, его длина равна 8. Найти координаты
M
, если
её абсцисса отрицательна.
6. Найти орт вектора kjia ⋅−⋅−= 22.
7. Найти скалярное произведение векторов ba
⋅
−
⋅
23 и ba ⋅−⋅ 65 если
6,4 == ba и угол между векторами a и b равен
3
π
.
8. Определить угол между векторами kjia ⋅+⋅+⋅= 543 и
kjib ⋅−⋅+⋅= 354.
9. При каком значении m векторы jima +⋅= и kjib ⋅+⋅−⋅= 433 пер-
пендикулярны?
10. Найти скалярное произведение векторов
cba
⋅
+
⋅+⋅ 432 и cba
⋅
+
⋅
+
⋅
765,
если
()
()
()
3
,,,,3,2,1
π
=⋅====
∧
∧
∧
cbcabacba .
11. Найти единичный вектор, перпендикулярный векторам kjia ⋅++= 2
и
kjib ++⋅= 2.
12. Даны векторы kjia +⋅+⋅= 22 и kjib ⋅+⋅+⋅= 236. Найти b
a
Пр и
a
b
Пр .
13. Показать, что векторы kmjia ⋅++= ,
()
kmjib ⋅+++= 1 и
kmjic ⋅+−= ни при каком m не могут быть компланарными.
14. Найти векторное произведение векторов kjia +⋅+⋅= 52 и
kjib ⋅−⋅+= 32.
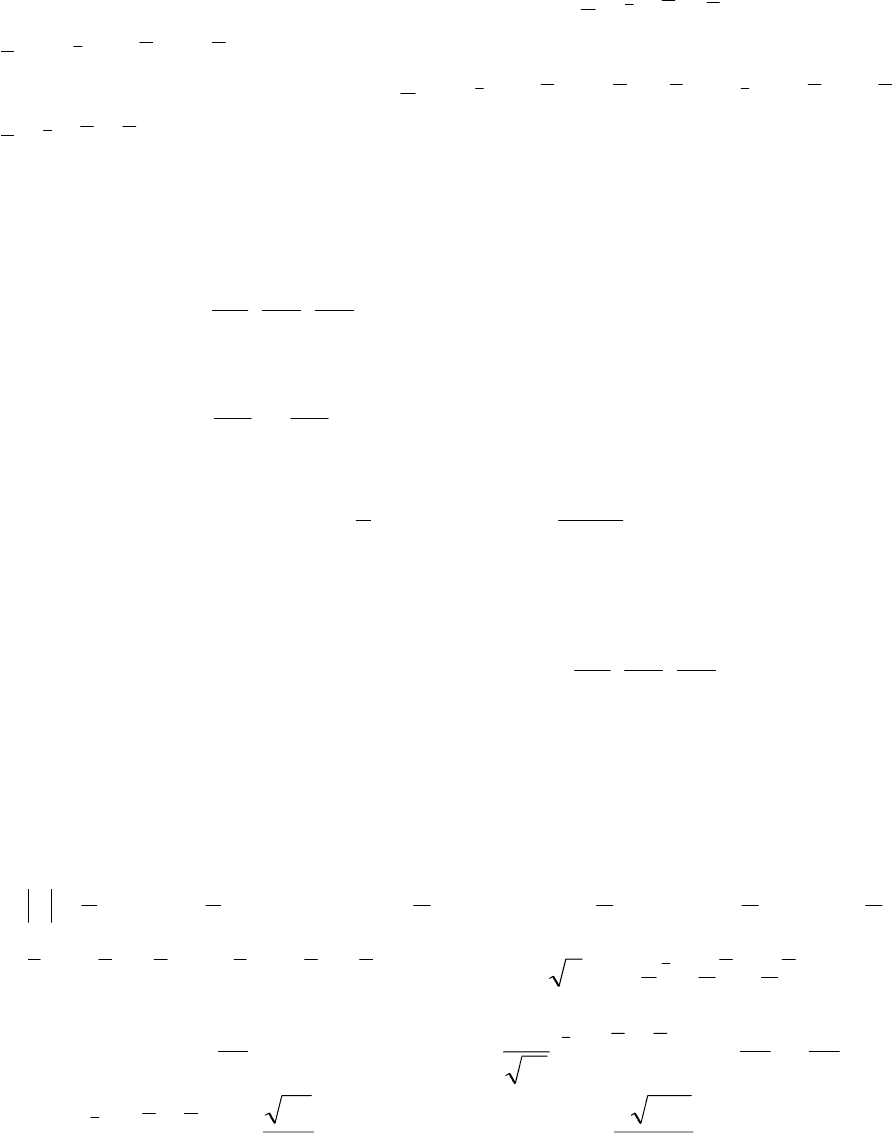
15. Вычислить площадь треугольника с вершинами
(
)
2,2,2A ;
()
3,0,4B и
()
0,1,0C .
16. Найти смешанное произведение векторов kjia +−= , kjib
r
r
r
r
++= ,
kjic ⋅+⋅+⋅= 432.
17. Показать, что векторы kjia ⋅+⋅−⋅= 237, kjib ⋅+⋅−⋅= 873,
kjic +−= компланарны.
18. Найти объём треугольной пирамиды с вершинами
(
)
1,0,0A ;
()
5,3,2B ;
()
3,2,6C и
()
2,7,3D . Найти длину высоты пирамиды, опущенной на грань
B
CD .
Указание:
1) найти векторы
ADACAB ,,
;
2) найти их смешанное произведение;
3) вычислить объём пирамиды;
4) найти векторы
В
С и
B
D и найти площадь
B
CD
∆
с помощью векторно-
го произведения;
5) использовать формулу
ABC
осн
S
V
hhSV
⋅
=⇒⋅⋅=
3
,
3
1
, вычислить высоту.
19. Показать, что точки
()
2,7,5
−
A ;
(
)
2,7,3B ;
(
)
4,4,9
−
C и
()
0,5,1D ле-
жат в одной плоскости.
Указание:
Точки лежат в одной плоскости, если векторы
ADACAB ,, лежат в одной
плоскости (компланарны). Проверить, что смешанное произведение этих
векторов равно нулю.
Ответы:
2.
5
3
=a ;
3
1
cos =α ;
3
2
coscos ==
γβ
; 3. 7;
7
2
cos =α ;
7
6
cos −=
β
;
7
3
cos =
γ
;
4. kjb 52 +−= или kjb 52 −−= ; 5.
(
)
24;4;4−M ; 6. kji
3
2
3
2
3
1
−− ;
7. 96− ; 8.
⎟
⎠
⎞
⎜
⎝
⎛
50
17
arccos ;
9. 1; 10. 547; 11.
(
)
kji +−± 3
11
1
; 12.
3
20
и
7
20
;
14. kji −+− 717 ; 15.
()
2
ед.
2
65
;
16. 4; 18.
(
)
3
ед20 ,
17
5104
.
Раздел III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Основными понятиями аналитической геометрии являются простейшие
геометрические образы – точки, прямые, плоскости, кривые и поверхности
второго порядка. Основными средствами исследования в аналитической гео-
метрии служат метод координат и методы элементарной алгебры. Возникно-
вение метода координат, тесно связано с бурным развитием астрономии, ме-
ханики и техники в 17 веке. Изложение
метода и основ аналитической гео-
метрии было сделано Р. Декартом, а дальнейшая разработка связана с труда-
ми П. Ферма, Г. Лейбница, И. Ньютона, Л. Эйлера.
Основная идея метода координат состоит в том, что геометрические
свойства линии выясняются путем изучения аналитическими и алгебраиче-
скими средствами свойств уравнения этой линии.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
НА ПЛОСКОСТИ
§1. Введение
Рассмотрим на плоскости прямоугольную систему координат
x
yO
.
Уравнение, связывающее координаты
x
,
y
называется уравнением ли-
нии
L
, если:
1) координат
x
,
y
всякой точки М линии
L
удовлетворяют этому уравнению;
2) координаты
x
,
y
всякой точки, не лежащей на линии
L
, не удовлетворяют
этому уравнению.
Взаимное расположение двух линий
Чтобы выяснить, есть ли у двух
(
)
0,
1
=
yxf
и
(
)
0,
2
=yxf
общие точки,
составляется система:
(
)
()
⎩
⎨
⎧
=
=
.0,
;0,
2
1
yxf
yxf
Число общих точек линий, равно числу решений системы уравнений.
Пример.
Найти точки пересечения прямых
5
=
+
у
x
(1),
102
−
=
−
y
x
(2),
10=+ y
x
(3).
Решение:
Составляем первую систему
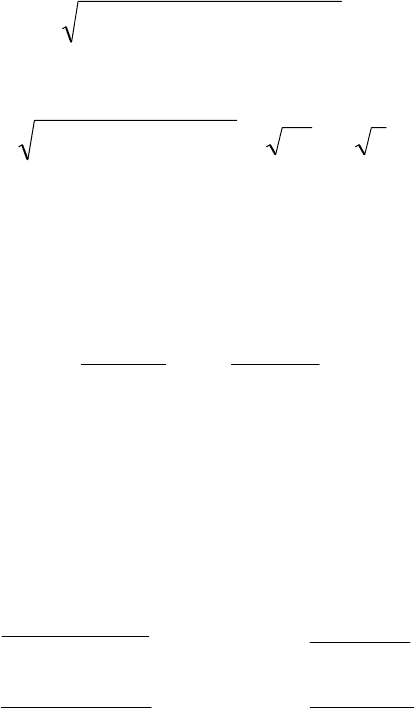
⎩
⎨
⎧
−=−
=
+
.102
;5
yx
yx
Решение системы
(
)
5;0 точка пересечения прямых 1 и 2. Ищем точки пересе-
чения прямых 1 и 3:
⎩
⎨
⎧
=+
=
+
.10
;5
yx
yx
Система несовместна, прямые 1 и 3 не пересекаются.
Расстояние между двумя точками
Расстояние
d
между точками
(
)
111
; yxA
и
(
)
222
; yxA
вычисляется по
формуле
()()
2
12
2
12
yyxxd −+−= .
Пример.
Расстояние между точками
()
3;0A
и
(
)
7;2B
равно
()()
52203702
22
==−+−=d
.
Деление отрезка пополам
Координаты середины отрезка
21
AA равны полусумме координат его
концов:
2
21
xx
x
+
=
;
2
21
yy
y
+
=
.
Деление отрезка в данном отношении
Даны точки
()
111
; yxA
и
(
)
222
; yxA
. Требуется найти координаты
x
,
y
точки М делящей отрезок
21
AA
в отношении
λ=
=
2121
:: mmMAMA
.
Решение дается формулами
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+
+
=
+
+
=
;
;
21
2112
21
2112
mm
ymym
y
mm
xmxm
x
или
⎪
⎩
⎪
⎨
⎧
λ+
λ+
=
λ+
λ+
=
.
1
;
1
21
21
yy
y
xx
x

Способы задания линии на плоскости
1.
()
−= xfy явный
(
)
743
2
−+= xxy
;
2.
()
−=ϕ 0, yx неявный
(
)
4
22
=+ yx
;
3.
()
−= trr векторный;
4.
()
()
⎩
⎨
⎧
=
=
;
;
tyy
txx
− параметрический
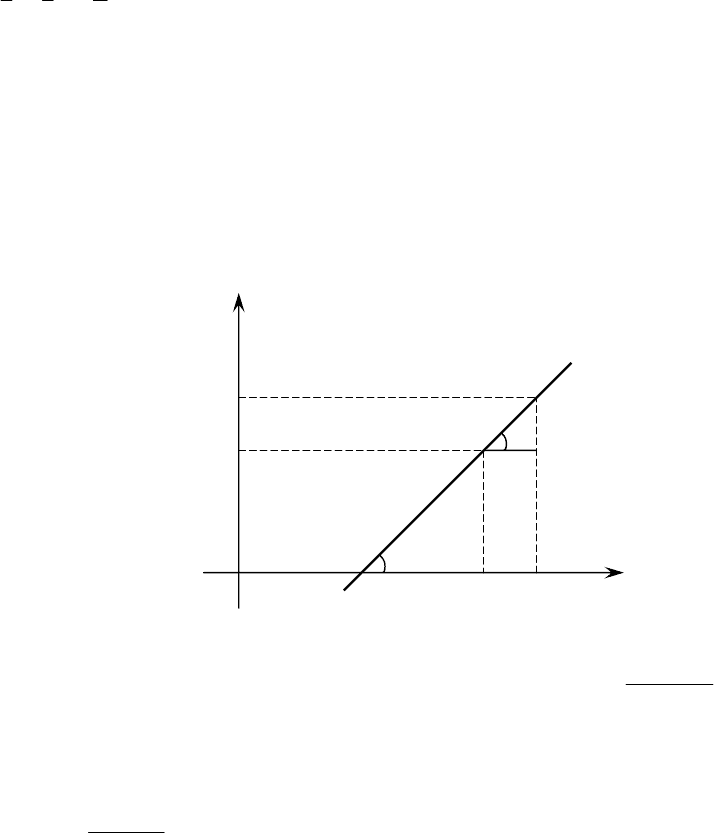
§2. Прямая на плоскости
На плоскости прямая чаще всего задается уравнениями вида:
1)
bkxy +=
– уравнение прямой с угловым коэффициентом (для прямых не
параллельных оси
O
y
);
2)
0=++
C
B
y
A
x
− общее уравнение прямой;
3)
()
tаrr +=
0
− векторное уравнение;
4)
()
()
⎩
⎨
⎧
+=
+=
;
;
0
0
tmyy
tlxx
− параметрическое уравнение прямой.
Уравнение прямой с угловым коэффициентом
Тангенс угла наклона прямой к положительному направлению оси Ox
будем называть
угловым коэффициентом этой прямой:
ϕ
=
t
g
k
.
Рис. 1
Если
()
000
, yxM
и
()
111
, yxM
− точки на прямой, то
01
01
xx
yy
k
−
−
= . Пусть извес-
тен угловой коэффициент прямой
k
и точка на прямой
l
;
()
yxM ,
− произ-
вольная точка на прямой.
Тогда
0
0
xx
yy
k
−
−
=
, или
(
)
00
xxkyy
−
=
−
− это уравнение прямой, проходя-
щей через заданную точку
.
Преобразуем его:
00
kxykxy
−
+
= . Обозначим
00
kxyb −= , тогда
bk
x
y +=
− это уравнение прямой с угловым коэффициентом. Число
b
на-
y
1
y
1
M
0
y
0
M
ϕ
ϕ
0
0
x
1
x
x
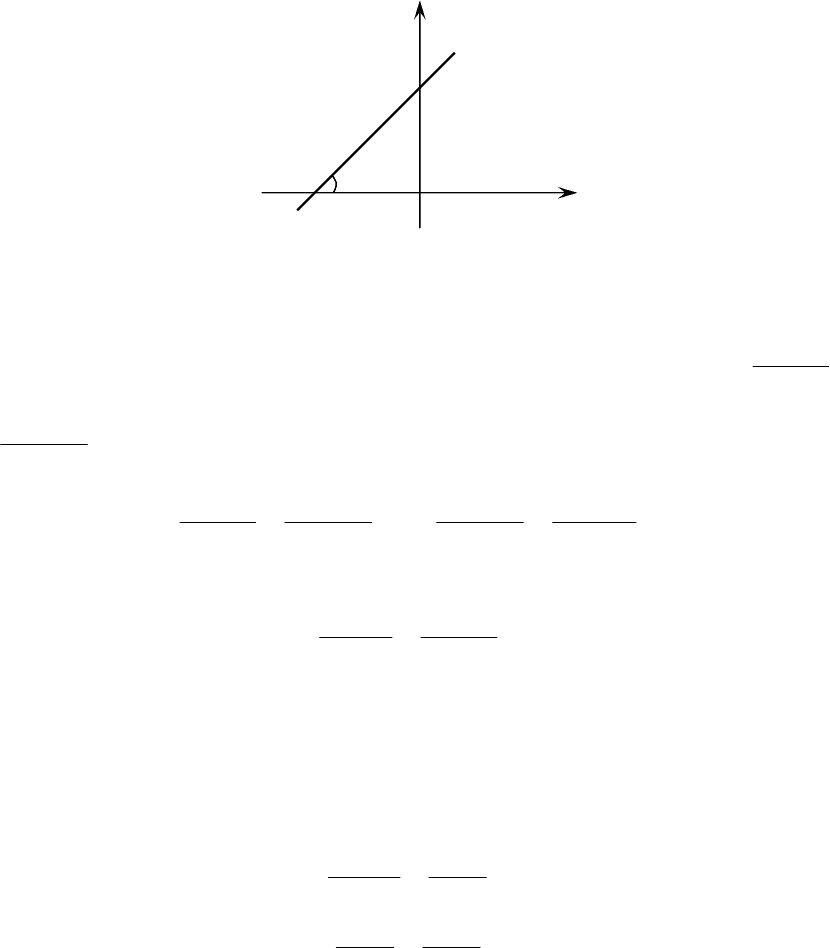
y
b
ϕ
0
x
зывается свободным членом. Геометрически число b равно отрезку, отсекае-
мую прямой на оси
Oy
.
Рис. 2
Уравнение прямой, проходящей через заданной точки
Пусть заданы точки
(
)
000
, yxM
и
(
)
111
, yxM
, т.к.
0
0
xx
yy
k
−
−
=
и
01
01
xx
yy
k
−
−
=
, то приравнивая, получаем уравнение
01
01
0
0
xx
yy
xx
yy
−
−
=
−
−
или
01
0
01
0
xx
xx
yy
yy
−
−
=
−
−
.
Обозначим
01
yym −=
,
01
xx
−
=
l
, получим
каноническое уравнение
l
00
yy
m
xx
−
=
−
;
вектор
{}
l,m
− направляющий вектор прямой.
Пример.
Составить уравнение прямой, проходящей через точки
(
)
3,2
0
M и
()
1,1
1
−
M .
Решение
Подставляем координаты точек в уравнение:
21
2
31
3
−
−
=
−
−
−
x
y
;
1
2
4
3
−
−
=
−
−
x
y
;
()
(
)
(
)
2431
−
−
=
−
− xy ;
После упрощений получаем уравнение
54
−
=
x
y
.
