Капутин Ю.Е., Ежов А.И., Хейнли С. Геостатистика в горно-геологической практике
Подождите немного. Документ загружается.


-геометрических
параметров
разведочной
сети
(ориентировки,
формы,
размеров
-
А),
-геометрических
параметров
проб
(ориентировки,
сечения,
длины
-
В
'
),
-пuраметров
функции,
характеризующей
пространственную
изменчивость
переменной
X(t)
(С),
-вида
оцениваемой
функции
(Р),
-вида
при.нятой
оценки
(ф).
Геостатистика
изучает
дисперсию
результатов
разведки
Й(Е)
как
функцию
от
перечисленных
аргументов,
чем
достигаются
две
цели:
-во-первых,
нахождение
таких
оценок
ф,
которые
при
заданных
значениях
прочих
аргументов
миними'зировали
бы
дисперсИю
Й(Е)
;.
-во-вторых,
определение
таких
параметров
разведочных
сетей
(А)
и
проб
(В),
которые
при
известных
параметрах
изменчивости
(С),
допустимой
дисперсии
Й(Е)
и
принитом
виде
оценки
Ф
минимизировали
бы
затраты
на
разведку
месторождения.
3.2.
Случайная
функция
как
математическu
модель
пространственной
перемеиной
Решение
практических
задач
требует
соглашения
о
типе
математической
модели,
к
которому
относится
функция
пространственных
координат
-
пространственная
переменная.
В
качестве
такой
модели
Ж.Матероном
предложена
случайная
функция.
Пространственная
переменная
X(t)
рассматривается
им
как
реализация
случайной
функции
F(t).
В
этом
случае
х
-
точка
или
вектор
евклидова
пространства.
В
результате
проведения
геологических
наблюдений
(опробования)
имеется
только
одна
реализация
случайной
функции,
и
проблема,
которая
при
этом
возникает,
заключается
в
том,
чтобы
найти
такие
характеристики
F(t),
используя
которые
можно
бьmо
бы
найти
неизвестные
значения
случайной
функции
пространственной
переменной
.
Каждая
случайная
функция
определяется
следующими
характеристиками
121):
-математическим
ожиданием
-
неслучайной
функцией
M(F(t»,
значение
которой
при
каждом
(=
t
о
равно
математическому
ожиданию
M(F(t»;
-дисперсией
случайной
функции
-
неслучайной
функцией
D(F(t»,
значение
которой
при
каждом
значении
(=
t
о
равно
дисперсии
D(F(t~)
-ко_ариационной
фУllкцией
-
неслучайной
функцией
двух
переменныx
(t
и
t+h)
.
K(t,t+h)=Cov
[F(t),F(t+h)]=M{[F
(t
)
-
М(F(t»]
*
[F(t+
h)-
-М(F(t+
h
»]}
(3.1)
Orносительно
используемых
в
г
еостатистике
случайных
функций
высказываются
несколько
гипотез,
которые
в
различной
степени
отражают
особенности
геологических
пространственных
переменных
.
Наиболее
частной
является
гипотеза
стационарности
случайной
40

функции
в
широком
смысле.
Она
предполагает
ВЫПОJЩени~
двух
условий
:
-во
-
первых,
матемаmческое
ожидание
случайной
функции
должно
быть
постоянно
в
пределах
изучаемого
объекта
(M(F(t»
= m =
const);
-во:-вторых
,
ковариационная
функция
случайной
функции
должна
зависеть
только
от
разности
аргументов
(K(t,t+h) =
K(h»,
.
а
не
от
положения
точек
t
или
t+J1
в
пространстве;
в
этом
случае
O(F(O)
==
к
(h
==
О
)
==
const
,
то
есть
дисперсия
случайной
функции
конечна
в
каждой
точке,
из
чего
следует,
что
случайная
функция
имеет
конечную
ковариацию.
Однако,
как
показано
Д.Криге
(5),
на
многих
месторождениях
не
существует
конечной
дисперсии
таких
пространственных
переменных
как
содержания
полезных
компонентов.
Тем
не
менее,
обычно
существует
конечная
дисперсия
приращений
этих
пространственных
переменных,
то
есть
проявляется
стационарность
nриращениЙ
.
В
этом
случае
допустимо
следующее
предположение:
М[F(t+
h)
- F
(t)]
==
О
(3.2)
Дисперсия
приращений
O[F(t+
h)
- F
(t)]
==
м
{F
(t
+
h)
- F
(t)
-
М
[F
(t
+ h ) - F
(t)]}
2 (3.3)
и,
так
как
М[F(t+
h)
- F
(t)]
==
О
,
то
О
[F(t+
h)
- F
(О]
=
м
[F
(t
+
h)
- F
(t)]
2 • (3.4)
Дисперсия
приращений
как
функция
разности
аргументов
h
в
математике
известна
как
структурная
функция;
в
геостатистике
ее
принято
называть
вариограммой
y(h)==tM[F(t+h)-F(t)]2
(3.5)
Эта
функция
может
быть
представлена
также
в
следующем
виде:
2y(h)=-&fv[F(t
)-F(t+h)]2
dt
,
(3.6)
где
V -
объем
месторождения.
Если
случайная
функция
стационарна
в
широком
смысле,
то
~e
приращения
также
стационарны,
а
вариограмма
определяется
соотношением
2y(h ) ='0
[F
(t
+
h)
- F
(t)]
=
о
[F
(t
+
h)]
+
о
[F
(t)]
-
2Cov[F(t
+
h)]
. (3.
7)
чем
определяется
с
оотношение
(связь)
вариогра.ммы и
КО8ариаЦUОН1IОЙ
функции:
y(h ) =
к
(О
) -
к
(h)
. (3.8)
3.3.
Вариограмма
как
х
арактеристика
свойств
месторождений
IlOлезных
ископаемых
Вариограмма
я.вляется
функцией,
анализ
которой
служит
основой
для
решения
задач
геостатистики.
Ее
построение
способствует
уточнению
представлений
о
разведуемом
месторождении,
особенно
на
ранних
стадиях
геологоразведочных
.
работ.
Вариограмма
отражает
различие
з
начений
геологической
пространственной
переменной
в
точках,
расположенных
на
некотором
расстоянии
друг
от
друга,
и
позволяет
о
енивать
погрешность
разведки.
Вместе
с
T~M.
из
соотношения
(3
.8)
вытекает
80ЗМОЖНОСТЬ
определения
взаимосвязи
41

(ковариации)
р
'
азобщенных
в
геометричес
ом
поле
значений
пространственной
переменной
.
Таким
образом,
в
вариограмме
отражаются
некоторые
свойства
месторождений
полезных
ископаемых,
учег
которых
важ~н
ДfLЯ
их
разведки.
К
этим
свойствам
относятся
непреРЫВНОСТЬ
-
l1рерывистость
оруденения
,
анизотропия
пространствеlJНОЙ
l1еременной,
пределы
проявления ковариации
значений
простран
ст
веllНОЙ
перем
ен
ной
в
окрестностях
точек
опробования.
Непрерывность
орудененuя
отражается
в
поведении
вариограммы
при
небольших
значениях
h.
На'чальное
значение
вариограммы,
равное
нулю,
и
постепенный
рост
ее
значений
по
мере
увеличения
11
характерны
для
непрерывных
пространствеНI:fЫХ
переменных:
для
геометрических
переменных
(мощности
рудных
тел
,
гипсометрических
отметок
их
поверхности и
т.д.)
и
содержаний
полезных
компонентов
месторождений
с
рассеянной
минерализацией,
в
основном,
осадочного
происхождения
(рис.3.1).
Содержания
многих
эндогенных
месторождений
характеризуются
резкими
изменениями
на
очень
небольших
расстояниях,
то
есть
8
поведении
этих
пространственных
переменных
ПРОЯВJIяются
скачки.
Соответствующие
вариограммы
характеризуются
TUK
называемым
эффектом
самородков
для
значений
аргумента
11,
близких
нулю,
(рис
.
3.2).
Зона
(интервал)
влияния
А
значений
пространственной
переменной,
замеренной
в
точке
опробования
или
в
разведочной
выработке,
(зона
влияния
пространственной
переменной)
соответствует
такому
значению
аргумента
11,
при
котором
вариограмма
выполаживается;
в
этом
случае
сама
вариограмма
прио
р
етает
значение,
равное
дисперсии
ПРОСl'раllСl'венной
перем
енной
(рис
.
З
.
J,
3.2).
При
значении
аргумента
1
1,
равном
зоне
ВЛИЛИЮI
пространственной
персмещюй,
согласно
(3
.2),
ковари
а
ци
о
ltная
функция
обращается
в
нуль.
В
связи
с
этим
интернал
W1ияния
про
странственной
переменной
принято
также
называть
интервалом
(радиусом)
кооариации
(корреляции
или
автоко
у(ь)
DIX(t)]
h
L-
______________
~
____
.
_______
_
~
~
---------
------------------
--------------------~
РИС
.
3.1.
Вариограмма
непрерывной
лространственной
переменной;
f)(X(t»
-дисперси
я
(или
порог)
пространственной
переменной;
А
-
интервал
ее
ВJlИЯНЮl
.
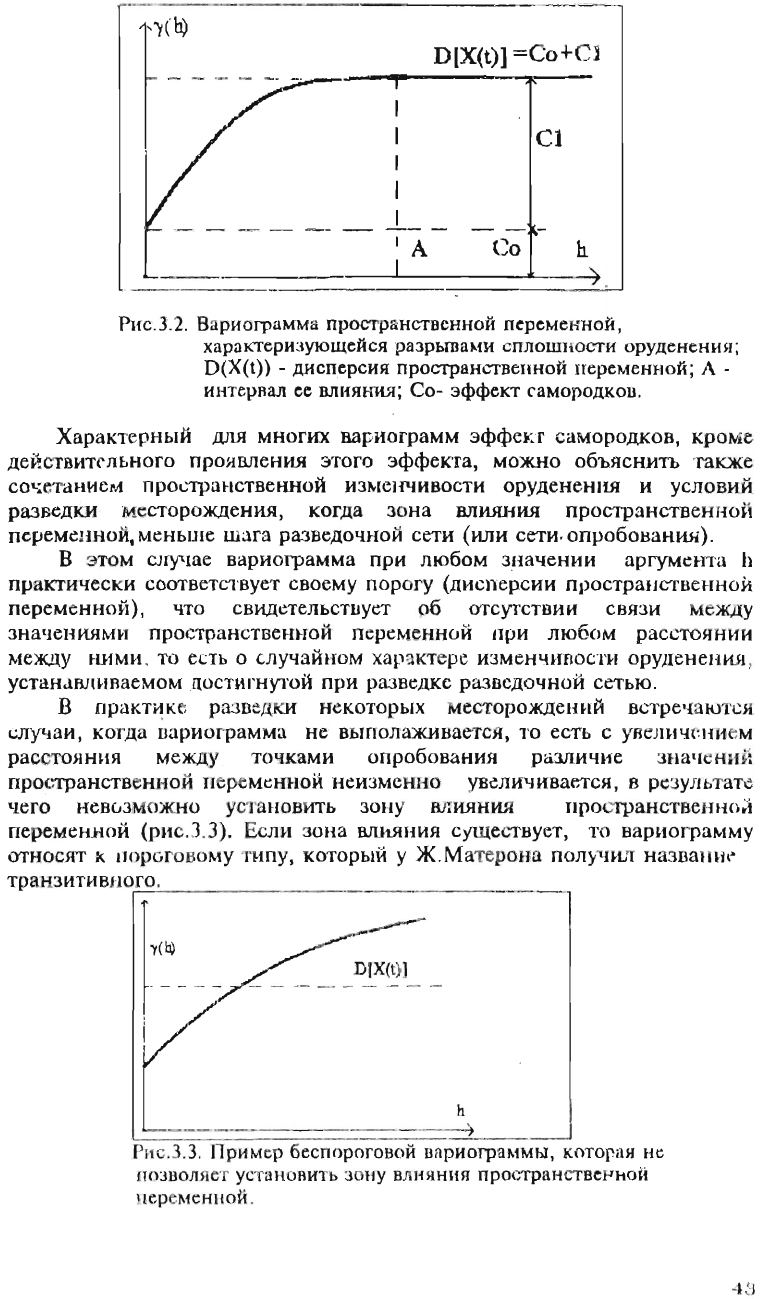
D(X(t)]
=Со+С]
I
I
-1--
'А
Сl
Со
ь.
РИС
.
З
.
2.
Вариограмма
пространственной
переме
н
ной,
характеризующейся
разрыпз}.{И
с
плош
ности
оруденения;
D(X(t» -
дисперсия
пространственной
переменной;
А
-
ин
терв
ал
ее
влия
н
ия;
Со-
эффект
самородкоп.
Характерный
ДJlЯ
многих
вариограмм
эффект
самородков,
кро
ме
действительного
проямения
этого
эффекта,
можно
объяснить
также
сочетанием
пространственной
изменчивости
оруденения
и
условий
разведки
место
рождения
,
когда
зона
влияния
пространстве
нной
переменноЙ.меньше
шага
разведочной
сети
(или
сети
~
опробования)
.
В
этом
случае
вариограмма
при
любом
значении
аргумента)}
практически
соответствует
своему
порогу
(дисперсии
пространственно
й
перем
енной),
что свидетельстuует
об
отсугствии
связи
между
значениями
пространствеююй
переменной
при
любом
расстоян.ии
между
ними
,
то
есть
о
случа
йн ом
хар
а
ктере
изменчивости
оруденения
,
устана8JIипаемом
достигнут
ой
при
разведке
разведочной
сетью
.
В
практ~ке
разведки
некоторых
месторождеЮ
IЙ
встречаются
случаи,
когда
вариограмма
не
выполаживается,
то
есть
с
уnеJ1
И
Ч
.
НИ
м
расстояния
между
точками
опробования
р
а3JIич
ие знач
ни
й
пространет
в
енной переменной
неи
зменно
увеличивается,
в
рез
у
льтат~
чего
невозможно
установит
ь
зону
влияния
ПРОl."lpанственно
Й
переменной
(рис
.
З
.
З)
.
Если
зона
ВЛИЯНИЯ
сущест
вует,
то
вариограмму
относят
к
ЛОРGГОВОМУ
типу,
который
У
Ж
.
Матерона
ПОЛУЧЮI
названи
~
траНзитивноrг
_
о
_
,
____________
____
. ____________
__
.,..,------
DIX(t)]
ь
--
- -
-4
__
P'iC
,3.3.
При
мер
беспороговой
вари
огр
аммы,
которая
не
1I0З130ляе
т
ус
т
анови
т
ь
зону
влияния
пространстве
Н
hОЙ
вер
меНIIОЙ
.
4
:-3

Анuэоmроnu.я
пространс
венной
переменнои
легко
определяется
построением
вариограмм
по
р
азли
чным
наl1равлеНШ1М
геометрического
поля
.
Она
может
выражаться
,
прежде
tl
t:f'O, lJ
ра
ЗJl
ИЧИИ
зон
влияния
лространственной
переменной
в
различных
нап
равл
е
ниях
.
Такая
анизотропия
часто
носит
чисто
г
еомеmрuчt,1СКUй
характер
и
может
быть
y(~
paHe
,
Ha
афинны
м
пре06разов
а
ни
ем
аргумен
а,
то
есгь
такой
заменой
аргумента
вариограммы
умножени
е
м
его
н
а
оэ
ффициент
(или
коэффици
енты)
преобразования,
к
оторая
делuет
ПРОС'lранственную
переменную
изотропной
(рис
.
З.4)
.
Последующая
оц
е
нка
простр
а
нст
в
нной
ll
е
ремеююй
осуществляется
с
учетом
этих
и
скажений
геометрического
поля
.
Однако,
рассмотренные
прос
т
ые
соотношения
вс
т
речаются
не
всегда
.
В
а
рио
граммы
по
различным
направлениям
могут
отличаться
формой,
характером
поведения
при
значе
ния
х
аргумента,
прежд
е
всего,
в
области
малых
величин
.
В
этих
случа
ях
можно
констатировать
наличие
функциональной
(или
з
ональноii)
анизот
роп
ии
(рис.
З
.5
)
.
Функциональная
анизотропия
нередко
может
быть
обусловленu
измеНЧНDОСТЬЮ
оруденения
,
связан
ной
с
ПР
О
S1W1
е
нием
суммы
двух
не
з
ависимых
СОСТ'
ВJlЯЮЩИХ
,
что
характ
е
рно
для
рас
сло
енных
з
алеж
ей:
-изотрошюй
компоненты
и
-зо
нальной,
которая
зависит
01'
чи
с
ла
пересекаемых
слое
в
.
Различия
значений
простраНСТR~ННОЙ
перем
ен
ной
в
сравниваемых
точках
опробования
определяются
в
данном
случае
не
т
олько
раСС'I'Оянием
между
ними, но
также
их
положением
н
расслоенной
рудоносной
толще.
Это
явление
известно
также
как
эффек
т
включения
(то
есть
как
эффект
включения
в
общую
и
'
м
енч
ивость
зонально.~
составляющей).
3.4.
РегуляризаЦliЯ
ЦРОСЧJанственной
цеременной
Вид
вариограммы
и
ее
хараk"reРИСТИКИ
(пр
едел
ьное
зн
nч
е
ние
-
ее
п
орог,
эффект
самородков
,
интервал
влияния)
з
ависят
не только
от
с
войств
пространственной
переменн
ой
месторожд~ния,
но
и
о
т
услов
и
й
его
разведки.
Если
пр
остран
ственной
пе
реме
нной
Я8Лнется
содержание
полезног
о
компонент
а
в
руде,
то
вариограмма
зав
исит
также
от
ориентир
овки
,
формы
и
ра
змеров
проб,
в
которых
опредеJUJ
тся
это
содержание.
РИС
.
З.б
демонстри
рует
влия
ние
на
в
ар
и
оrра
мму
изменения
Д1Jины
про
б
.
Увеличение
размера
проб
(ге
ометр
ической
бu
:
sы
прос
тр
анстве
нн
ой
переменной)
приводит
К
регу~ризации
пространственной
п
е
р
еменной,
,
{то
отража
ется
на
нар
иограмме.
В
этом
случае
У"
f
еньшаетс
я
дисперсия
про
ст
р
а
нств
енной
п
е
ременно
й,
увеличивает
SI
ее
зона
влияния
и
СНИJкастся
э
ффек
т
сам
ородков
вариограммы
.
Геометри
lеская
база
пространственной
I1сременной
являетс
я
ее
весовой
функцией
.
44

-
--
-
---------
-_.-
y(~
DIX(t»)
I
'Аl
'Л
2
11
__
_ J
______
_1-_.
_
___
_
_____
-)
Pit
с~ 3
~.г
Вill
.;
и
ОГр
аМ~lы
дл
я
дн
у
х
IJ
Зi\II
МiiO
пё
рл
енцик
у
ЛJ
'Р
Н
ЫХ
lIаПР
:
\l
зле
ний
геометриче
с
кого
IЮ
)
НI
МС
Сl'
UРО
Ж
Д
t;
НШI
,
о
р
а
ж
аЮЩIIС
ге
о
ме
Т
РИЧеСКУЮ
аНИ
:
Ю
Т
РОI
I
ИIU
.
D(Л(I
)
!
2
__
"'i
-
-";"
~:"'::""-
I
I
_
.-I--
-
--t
D(ХЩ)
1
I
I
:,
. __
1A1
_____
~,
J
Рис
-
:S
:
А:
ii ;
i
fо
гра
-;:
lМ
bl
Д
IН
I
д
вух
направлений
i~u
м
ет
rичсс"ого
rю
л я
,
отра
ж
ающие
З,Чlальную
аНl:ЗО
Т
РОIlИЮ
~Н~
С
ТОРОЖДСН
и
11
.
Е
с
ли
X(
I)
rJр
ос
траllстnенная
пер
меннан
на
точечной
l'e
uM
C
I]H1'I
eC
KOIi
б
ilЗС,
а
v -
н
е
ко
т
орые
рt:алЫlые
о
б
ъеМ!..1
I1
L
~ледуеМ\JI'О
ео
О
Г
И'lеск
о
{
'
о о б
ъ
е
к
т
а
11
зн
а
чешш
э
той
ПРОС11Jaнстненн
uй
н
е
ременной
Оllрt:д
ел
t:IIЫ
n
эт и
х
о б
ъ
е
мах
,
то
IIOНал
про
с
тр
а
llствен
н
ая
rн
:
р
t:.
менная
~i)
=
vJ
v
X(t+/)dl
(3.9)
отшl'Н1
ТС
SI
от
п
е
рuой
б о
л
ьUJ
'
JI
р
е
г
уля
рн
ост
ью
.
ФУНКI(ИН
y(t)
1Н11ыuае
тся
ФУНКШIt:Й
X(t),
реГУЛЯРН
З
ОD
а
н
но
й по
об
ъе
му
У
.
ЕСШI
p(l)
не
которая
в
е\,;О
В
t
ш
Ф
У
НКЦИЯ
,
ОllреJJ.еЛJ1СМая
uотношени
е
м
р
=
fp(/)d/
,
Те
n
общем
Ш1дt
У(д
= * f
X(t
+
/)d/
(3
. J()
Последовш
'
слыlO
С
ВЗБ
шивание
простран(.
'Т
в
е
нн
о
Й
•.
<
:
ремсtШОJl
на
зону
ВЛИЯНИJl
меньшей
размерности
-
точечной
п
е
ременной
на
линейную
зону
ВЛIIЯНИЯ,
линейной
переменной
на
ILJ
1ОUЩI1НУЮ
зону
влияния
11
В
якое
по
леДОВRтелыюе
сокраШ
,t
ние
Р
::I
МС:РНОСТIf
'
юны
ВЛИЯIfl1Л
в
е
р меНtlОЙ
в
11
-
мерном
простр
а
нстве,
Tu
е
'
Гt.
пер
е
х
JД
0 '(
fn(t
)
к
''' -1(0 , -
на
З
ЫJ:jаеlСЯ
rегул
рн
з
ацией
первог
о
п
о
f1ДKa
8
.1
tollЬ
ОСI1
t"
,
а
п
t:
р'
ХОД
от
',,(t
)
к
f
п
-
2
(t)
вдоль
IIЛО
С
КО
••
ТИ
t"
-
l,t
ll
рег
у
m.РИ
Зi
щи
е
Й
в
то рого
ПОРjlДl\
а
It
'Г
.д
.

._---------3.
~----------------b
h
Рис
.
З
.
б
.
ВариограММbl
содержаний
металла,
полученные
по
пробам
разной
длины:
а
-
по
коротким
пробам;
Ь
-
по
ДЛНННblМ
пробам.
в
том
'
СЛУ4ае,
когда
пространственН<ш
перемеННi)Я
изотропна
,
то
есть
ее
вариограмма
зависит
не
от
напраВJlеНИSI
вектора
-
аргумента
11,
а
только
от
его
модуля
IJlj
=
r,
где
в
н-мерном
пространстве
г=
Jh
1
2
+
hl
+ ... +
h~
-
(З
.
lI)
регуляризация
первого
порядка
может
быть
применена
к
оценке
вариогра.м'мЫ
регуляризоваШIОЙ
1Iере.меIlIlОЙ
по
Вi:tриограмме
'
исходной
переменной.
Соответствующий
алгоритм имеет
следующий
вид:
"(n-1(r
)=~f~
[(/-t)уп(J,
2+
t
2)]dt-~f~
(1
-
t)уп(t)
.
(З
.
12)
Используя
этот
алгоритм
или
алгоритмы
регуляри:заЦИl1
более
высоких
порядков,
по
вариограмме
flроетранственной
переменной
для
проб
малого объема
можно
оценить
вариограммы
проб
большого
объеу..
'
I:l,
блоков
различного
ра
з
мера
в
пределах
рудного
тела
или
месторождения
и
т.д.
Как
и
з
вестно
I1З
практики
геологора
з
ведо<mblХ
работ
и
видно
из
сопоставленин
вариограмм
лростраНСТВtННОЙ
перем
е
нной
при
различном
размере
проб
(рис
.З.
б),
по
мере
регулиризации
пространственной
переменной
снижается
cTellel·
lb
ее
варю,Щий
(41'0
отражается
в
уменьшении
вари
а
ций
значеllИЙ
самой
вариоrjJаммы)
и
предел,
)ос
которому
стремитен
вариограмма
(дисперсия
пространственной
переменной
или
порог
вариограммы)
.
Это
явление
может
быть
выражено
с
помощью
вспомогательной
функции
F
F(I)
=~f~
(1
-
g)y(g)dg
(3.13)
лредстаWUlющей
собой
среднее
значение
ваРИОI
'
раммы,
для
которой
g -
расстояние
между
двумя
ТО'lками,
независимо
одна
от
другой
занимающими
все
возможные
положения
"Ia
отре
з
ке
1.
Если
регуляризация
лространственной
переменной
связана
с
существенным
изменением
формы
и
ориентировки
геометрической
базы,
то
возникают
трудности
учета
весовой
функции
.
Ж.Мат
е
роном
введено
понятие
Аиllейного
эквUllиленmа
тела
flOJle:3HOrO
ИСКОl'lаемого
или
пробы, под
которым
011
ПОlJимает
геометри<,ескую
фигуру,
прмставляющую
еобой
отре
:
юк
ДJ
Нtlюit
1
ДНЯ
IIробы,
соде
рж
а
ние
lюле
J
НОГО
компон
е
нта
н
котором
обладает
то
й
же
дисперсиеll
внутри
46

большого
объема
У
,
что и
FI
реальной
пробе
объемом
у;
аНWЮfИЧНО
для
самого
тела
полеЗIIОГО
Ifскопаемого
V
принимается
линей
ный
эквивалент
L.
для
lJ::.хожден\'IЯ
линейных
эквивалентов
проб ИЛИ
тел
полезных
ископаемых
используется
вспомогательная
функция
F(l).
Jlин
ЙНЫЙ
ЭКUИВ:lJlt:НТ
t
пробы
v
определяется
ИЗ
соотношения
1111
= F(v) + 3/2. (3.14)
Определенltе
JIIН
<
lей//ых
эквивален
тов
различных
геометриqеских
фигур
прс:дстаВЛJl~Т
собой
достаточно
сложную
задачу.
В
к
ачестве
примера
можно
ПJ)JНI~СГИ
IrepUble
ЧЛt:ны
разложения
для
линейн
ого
ЭКВ И
J>алента
геомt>трнческоJ1
фигуры,
имеющей
форму
прямоугольного
параллелеl1ипеда
СО
СТОIЮН,\М1I
a>=h>=c:
I(
Ь
)
-
J
1[Р-
~
ь
~
1
ь
_
..2.5..й.:.
__
L_~
1
tfJ
а,
,С
-
па
+
за
+
б а
2
111
7 2
а
2 -
f80
а
4 +
1680
а
6 + .
...
+~~(ln2+~i)t+....
(3
.
15)
Для
приближ
е
нно
о
определения
этого
линейного
эквивалента
может
быть
использована
сл~дующаJ(
функция:
I(a,b,c) =
а
+
Ь
+
с/2..
(3
.1
6)
Эта
Функцнн
и
функции
ДJШ
других
геометрических
фиг
у
р
таБУЛl1рованы
и
предстамеНbJ
в
виде
IIOMOrpaMM
Ж
.
Матероном
1
2].
3.5.
дИСl1
рсия
Р"СllрuстраН~IIИЯ
как
ошибка
разведки
м~сторождешtЙ
пuлезных
ископаемых
в
основе
ОЩJtДС:Л
ё
IIШI
ПОI
'
решностей
разведки
месторождения
л
е
жит
rЮНЛТllе
дн
с
пс;:рс
.И
распростраНt:нин,
которая
представляет
собой
меру
рассеивания
(так
назывпе
fУЮ
ошибку
анШIОГИИ'
средних
значений
l
'
tОЛОПI
"
ССКИХ
fшраМ
tТРО8
n
I
-
Iсисслед('ванном
объеме
тела
полезного
иско,шсмого
V
ПО
их
известным
оц
I-Iкам
в
опробованном
объеме
(В
суммарном
uбъеме
опробованных
развеДОLIНЫХ
выработок)
VJ.
В
каче
с
тuе
Д
IIСI1СРС!
ираспрос
'
ранеllИЯ
рассмаТРJlвается
дисперсия
О(У
- Z) =
П
(
У)
+
D(Z)
- 2Cov(y,Z),
где
У
-
среднес:
:
ща'lеlше
п
ере
менной
в
объеме
У;
Z -
то
же
в
объеме
Уl;
О(У)
-
диспеРСЮI
переменно~,
в
объеме
У;
D(Z)
.-
то
ж
е
Б
объеме
V
1;
C()v(Y,
Z)
-
хоrшриаЦllЯ
обеих
оценок.
(3,17)
Эта
Дlн;пер
с
ин
С
JJУЖИТ
ДJ1Я
8ЫР"ЖСНIIЯ
ошиб
'
]1.
с
которой
среднее
значенне
про",гранствеНII
й
п
е
р
еме
нной
в
объ~ме
V t
может
быть
ПРИНflТО
в
Ю\'lеС
'
1
ве
среднего
значения
8
объеме
У,
или
шюборог
,
Дисп
реил
rаСГlростrаненин
имее,
'
СJf~ДУЮЩ
JlЙ
hид
D(Y
-Z
)
~-.:
-;;
f
v
Jv
(К
(t
- t ,»)dtdt, +
~
f
V1
Jv
1
(К
(t
-
ll»dt
'
-
v~,-
Jvfv,
(К
(t
-
t,»dtdt
l
_
(3
.
18)
Если
вм
е
с
то
j'MM(}PIIOI'U
объема
\'
t
рассма
l
'
рШ3<1
t.
ДJl(
.
креТIlУЮ
СОВОКУШfOСТl-
"
сос
опщую
и
з
N
точ~к
t1,
... , t N ,
то
неЛНЧШiа
Z
опреД
~
JUI~ТСЯ
IЫlшжеНl1ем

Z~*L~,
(f(t;).
(3.19)
В
е
личина
Z
предст
а
вляет
собой
среднее
значение
r:Iр
остранственной перем
ен
ной
X(t)
в
N
точечных
пробах.
В
этом
случае
диспер
с
ия
распростр
ане
ния
характери
зуе
т
ошибку,
с
которой
среднее
значение
У
пространственной
переменной
X(t)
в
объеме
V
оцеНИВ:1ется
величино
й
Z,
полученной
по
N
точечным
пробам
.
Эта
дисперсия
является
дисперсией
оценки
месторождения.
Используя
формулу
(3
.18),
для
дисперсии
оценки
получаем
D(Y-
Z ) =
v7
fvfv(К(t
-
t,)dtdt,)
+
-,}-2
L:.f
J
=,
К
(tj
-
tj)-
- N 2
v
L~,
f v
K
(!
- t ,
)dt
.
(3
.20)
Если
v
и
V -
два
объема,
первый
из
которых
содержИтся
80
втором
,
а
Z
и
У
-
средние
стохастические
значения
функции
X(t)
в
этих
объемах,
то
дисперсия
распространения,
характеризующая
пог-решность
оценивания
среднего
значения
У
в
объеме
V
средним
значением
Z
в
объеме
У,
полностью
определяется
формулой
(3.18).
для
краткости
эта
дисперсия
называетен
дисперсией
распространения
v
на
У
.
Когда
геометрическое
поле
V
сложено
элементами
одинакового
объема
У,
дисперсия
v
в
V
определяется
следующим
выражением:
D(v/V)
=
~
ff
vy(t-
t,
)dtdt,
- -;;
ff
v
y(t-
t
,)dtdt,
. (3.21)
Эта
формула
приводит
к
соотношению
аддитивности,
которое
известно
как
формула
Криге:
D(vIVl)
= D(vIV) +
D(VIVl),
(3
.22)
которое
показывает,
что
дисперсия
v
в
Уl
равна
сумме
дисперсий
vвVиVвVl
.
Дисперсия
распространения
из
формулы
(3
.
18)
может
быть
представлена
как
дисперсия
оц
ен
ки
:
а:
=2y(S,A)-У(S,S)-У(АА)
,
(3.23) .
где
'
у(
S,
А
) -
среднее
значение
вариограммы
между
каждым
разведочным
пересечением
и
каждой
'
точкой
оцениваемого
объема
(это
кова
риац
ия
выборочной
оценки
блока
с
истинной
величиной);
у(А
А ) -
среднее
значение
вариограммы
для
всех
комбинаций
пар
точек
внугри
оценив
аем
ого
объема
(это
присущая
блоку
характеристика
изменчи
вости
;
она
выражае
тс я
функцией
1:
(1)
,
где
I =
У;
y(S,
S)-
вариограмма
ДJUI
всех
комбинаций
разведочных
llересечениЙ.
Вариограмма
у(
S,
А
)
представля
ет
собой
вспомогательную
функцию
Х
х(l)
= t
f~
y(f)dt.
(3.24)
Выражение
(3.23)
иначе
может
быть
пр
едстаме
но
как
а:
=
2х
(1) -
y(/)
- F
(1)
.
(3.25)
3.6.
Применение
спектрального
анализа
ДЛЯ
ОllисаНIIЯ
измеtlЧИВОСТИ
проt.-транственных
переменных
Н
аряду
с
исп
ол
ьзо
ванием
структурного
(при
помощи
вариограмм),
корреляционного
(ковариационного)
анал
и
за
пространственных
48

п~р~менн
lX
lJ,JlИ
описания
их
измен'/ивости
может
бьа
ть
.,
'
акжс:
и
споль
:
юван
сп
кТ(цлъный
анализ,
что
предусматривает
ПРИ8Jlечение
поняl'ИЙ
га
р
t.ЮIfИЧ
c~oгo
ра
ЗJl
оженнн
(Рl.\ЗЛожения
в
гаРМОНИ'l
ес
кий
РЯД
или
РЯД
Фурье)
Вi>ОСl
р
сшс
8
~
HHЫX
пер
сме
НIiЫХ.
представляющего
собой
ком
по
зицию
их
Флуктуаций
различных
частот
,
и спектра
диспер
с
ий
114
,1
51
· .
Ри
дом
Фурье
может
быть
представле
на
любая
функция
.
УДОВЛ\
~Т
Iюршощан
УС.l
ЮDШJМ
ДИРИ:<JIе:
функция
на
интернме
р
а:.vю
жr.НЮJ
JIВЛН~J
'С
Н
U/"pl.llllf'leIlHOJI,
кусочно-непрерывной
и
имеющей
конечное
ЧI\СЛО
экстрсмалъных
значений
.
Геологи
lеская
npo
(';тpaHC'I'l
'
lIшm
перемснная
X{
t),
задан
ная
на
интервале
(-Т,Т),
мож
е
т
быть
UbI
p.
ж
е
на
рядом
Фурье,
J\(t}
=
~
+
':;
.:
1
(дк
C."
ft,SW
I\
·t +
Ь
k
"I
..
w~
t)
(3
.26),
или
X(t)
~
~
+
}~~1
С
k COS'
(ffik
t -
Ч>k
)
(3
.27),
I 2 . 2
гцс
С
К
=
~
aA:
+
Ь
К
-
зм
ruШ
'
lуда
k-ой
l'аРJ\lЮНИЮ1,
фк
= k
Т
-
е:
частота
и
<РА:
=
arG
tg
(~:)-
нача
J
JЪШ1Я
ф
аза,
..
К
ОЭффl
'
JЦИ
II1Ы
дк
I
Ь
К
определяю
тс
я со
отношениями;
дк
::
f
f
~
(
x(t)CO
S(J
)k
Ю!
(3.28),
Ь
А
=
./
..
f~t
x
(t)"inCOk
tdt· (3.29).
Ряд
ФУРLе
З:lмен
н
етс
н
ин
те
гралом
Фур
ье
n
том
случае,
если
прост
р:шс
твеllll
'
Ш
lIерr.менная
X(t)
зад
ана
на
бесконечном
ю
·
rгеl)вале
-
00,00
l-IаГЛ>lдНОЙ
>.аlН1КтеристикоЙ
простравст
nенной
изменчивости
еОл<"ГИ
'Jе
скоii
I1сремеНilОЙ
X(t)
nвляетСiJ
сп
е
ктр
ква,цратов
амплитуд
rа(lМОНИК
C
k
,T.r..
енею
)
(ИЛII
спектральная
мотность
дисперсии;
ри
с.3
,
7)
. (2
2)
Sk
:;:
С;
1;
=
'4t~f
l
J:
+
/)
k . I k = 1 ....
00
(J
.
ЗО)
ВСЮ
{\lИна
Sk
выраЖJ.:'Г
долю
ДJlсп
е
рсии
пространстпснной
перем
е
нной
ХЩ
Н:1
интеР
В
ЮIС
(-Т,Т),
ПРИХ
О
Д>
IЩУЮСJl
на
гаРМОНltк
у
с
IIO~
ером
k.
_. __ .
__
._--
-_
.
_-
-
I
~~p~"""
'"
-_._------
___
о
_ .
____
____
ф
.
1
..
___
.
__
....
_
___
..
_____
..
_.
___
_
__
____
. __
Рllс.3
.
7
.
Общий
ВИД
граф
н
кu
~
'
/ieI<Tp
лыюй
ЛЛuТIIШ,
;
ТIt
с
преоБJНI)
.
Laниеr.1
u
дисш
,
р
(;
IIИ
ни
зки
х
ЧIIСТОТ
49
